Modul 8 Fis 2 - Universitas Mercu Buana

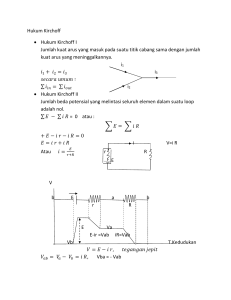
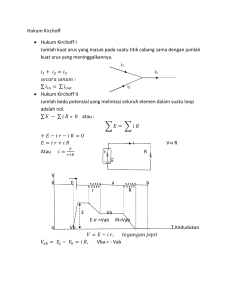
Modul 8. Fisika Dasar II
I. Induktansi,Energi dalam Induktor dan Konstanta Waktu
Tujuan Instruksional Khusus
Mahasiswa diharapkan dapat memahami dan menghitung besarnya induktansi pada
kumparan serta memahami konstanta waktu pada rangkaian RC dan RL.
II. Materi :
Induktansi,Energi dalam Induktor dan Konstanta Waktu
2.1 Induktansi
2.2 Energi dalam Induktor
2.3 Konstanta Waktu
III Pembahasan Materi
2.1 Induktansi
Suatu penghantar yang berbentuk gulungan atau lilitan yang disebut
sebagai
induktor. Induktor memiliki kemampuan untuk menyimpan energi dalam medan
magnet, dan ukuran yang menyatakan besar kecilnya kemampuan induktor energi
atau disebut induktansi.
2.1.1 Induktansi Bersama ( Induktasi Silang )
Terdiri dari dua kumparan yang dalam keadaan diam satu terhadap yang lainnya (
Gambar 6.6 ). Kumparan I terdiri atas N1 lilitan dan dihubungan dengan sumber
tegangan bolak-balik, sedangkan kumparan II terdiri atas N2 lilitan tanpa dihubungan
dengan sumber tegangan luar.
Akibat perubahan arus yang dihasilkan sumber pada kumparan I, fluks magnet yang
melalui kumparan II berubah terhadap waktu maka timbul GGL induksi pada
kumparan II. Hubungan tersebut dinyatakan sebagai berikut :
21
 N2
d 21
dt
d 21
d 21 di

dt
di dt
( 8.1 )
sehingga
d 21
 21 di1

dt
i1 dt
http://www.mercubuana.ac.id
( 8.2 )
Suatu kumparan yang memiliki N lilitan, jika kumparan tersebut diberi arus yang
berubah terhadap waktu maka fluks magnet dalam kumparan tersebut berubah
terhadap waktu. Sehingga akan terjadi GGL induksi di dalam kumparan itu sendiri.
Induksi tersebut dinamakan induksi diri, dan GGL induksi yang terjadi pada
kumparan ditentukan dari hukum Lenz-Faraday , sebagai berikut :
d m
dt
' N
( 8.5 )
atau dinyatakan dengan persamaan :
LN
m
i
L L
atau
di
dt
( 8.6 )
Contoh 1 :
Sebuah inductor terbuat dari kumparan kawat penghantar dengan 100 lilitan . Jika
panjang kumparan 16 cm dan luas penampangnya 8 cm2. Hitunglah :
a. Induktansi diri
b. Induktansi diri, jika kumparan disisipi antibesi dengan  = 500 o.
Penyelesaian :
LN
a.
m
o
i


(4 .10 7 )(100)2 (8.10 4 )
0,16
 2 .10 5 H
b.Jika terdapat antibesi, maka :
L  500.20H  0,0314Henry
2.2 Energi dalam Induktor
Karena inductor memiliki GGL-induksi ( GGL- Balik ), maka diperlukan usaha untuk
memperbesar arus dalam inductor dari nol sampai harga I. Usaha yang dilakukan
pada kumparan selama proses ini dihimpun dan disimpan, dalam kumparan/medan
dan akan diperoleh kembali seandainya arus dalam kumparan diperkecil kembali dari
I ke nol. Energi yang tersimpan adalah sebagai berikut :
W
1
2
LI 2  W  Joule
( 8.7 )
2.3.1 Konstanta Waktu RC ( RC- time )
b
a
a. Muatan q
Kapasitas mula-mula tidak bermuatan.
http://www.mercubuana.ac.id
S
a
c. Kuat arus pengosongan.
Bila kapasitor C yang mula-mula bermuatan qo=Q=CVab. Kemudian diberi
kesempatan melepaskan muatan itu melalui hambatan R, maka kurva
i→
t adalah sama dengan kurva waktu kapasitor sedang mengisi.
Muatan q pada kapasitor juga menurun dan mengikuti kurva seperti kurva
arus pelepasan. Pada saat t = RC, i = 0,37 io dan q = 0,37 Q
2.3.2 Tetapan Waktu RL
b
a
a
Gambar 8.2 Rangkaian RL
L
s
b
R
x
I = kuat arus pada waktu t
Vab 
 L
Ri
di
dt
di
Vab  Ri ( L
Vab L
i
di
dt
Vab
(1
R
Vab  Ri
dimana
dt
)0
dt
atau
Ri  0
atau
Rt
di
Vab L
Vab
L
L
di
Ri
dt
L
 Ri
0
tR
e )  i  I (1
L
e )
L
, I = kuat arus maksimum dalam rangkaian.
L/R = tetapan waktu dimana arus I mencapai harga I/e dibawah harga
maksimumnya.
Contoh 1 :
Suatu solenoida dalam udara panjangnya L luas penampangnya A dan jumlah
lilitan N.
a. Tentukan induksi diri solenoida itu
http://www.mercubuana.ac.id
( 8.9 )