Integral Permukaan

Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
KALKULUS MULTIVARIABEL II
Integral Permukaan
(Minggu ke-10)
Supama dan Hadrian Andradi
Jurusan Matematika
FMIPA UGM
Yogyakarta, Indonesia
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
1
Integral Permukaan Fungsi Bernilai Real
2
Penghitungan Integral Permukaan
3
Contoh Soal
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Diketahui S merupakan permukaan pada R3 yang diberikan oleh
grafik fungsi dengan rumus z = f (x, y) pada suatu daerah R yang
termuat pada domain f .
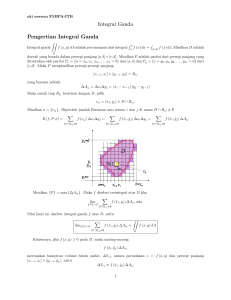
Misalkan partisi P membagi daerah R menjadi n bagian, katakan
R1 , R2 , . . . , Rn . Diambil sebarang i = 1, 2, . . . , n. Daerah Ri memberikan luasan Si ∶= {(x, y, z) ∣ z = f (x, y), (x, y) ∈ Ri }. Pada
daerah Ri diambil sebarang titik (xi , yi ) sehingga diperoleh titik
(xi , yi , zi ) pada luasan Si (lihat gambar pada slide berikutnya).
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Misalkan ∆Ai menyatakan luas dari Si . Selanjutnya, diberikan
fungsi g ∶ D ⊆ R3 → R dengan S termuat pada D. Didefinisikan
integral permukaan dari fungsi g atas S sebagai berikut
n
∬ g(x, y, z) dA = lim ∑ g(xi , yi , zi )∆Ai .
∥P ∥→0 i=1
S
Dengan memperhatikan
√
∆Ai ≈ (fx (xi , yi ))2 + (fy (xi , yi ))2 + 1 ∆yi ∆xi ,
diperoleh bahwa
∬ g(x, y, z) dA = ∬ g(x, y, z)
S
√
(fx (x, y))2 + (fy (x, y))2 + 1 dydx.
R
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Sifat Integral Permukaan
Diberikan fungsi g ∶ K ⊆ R3 → R dan permukaan S, S1 , dan S2
pada K. Jika S = S1 ∪ S2 , dengan S1 ∩ S2 merupakan himpunan
kosong, himpunan berhingga, atau gabungan sebanyak
berhingga kurva, maka
∫ g(x, y, z) dA = ∫ g(x, y, z) dA + ∫ g(x, y, z) dA.
S
S1
Supama dan Hadrian
S2
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
S1 ∩ S2 berupa titik
Supama dan Hadrian
S1 ∩ S2 berupa kurva
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Teorema Terkait Penghitungan Nilai Integral Permukaan
Diketahui S merupakan permukaan yang diberikan oleh
z = f (x, y) dengan (x, y) ∈ R. Jika f memiliki turunan-turunan
parsial orde pertama yang kontinu dan fungsi g dengan
g(x, y, z) = g (x, y, f (x, y)) kontinu pada R, maka
√
∬ g(x, y, z) dA = ∬ g (x, y, f (x, y)) fx2 + fy2 + 1 dydx.
S
R
Dengan memanfaatkan teorema di atas, untuk menghitung integral permukaan dari suatu fungsi tiga variabel, dapat dilakukan
dengan menghitung double integral dari fungsi dua variabel.
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Teorema Lain Terkait Integral Permukaan
Diketahui S merupakan permukaan mulus dua sisi yang
diberikan oleh z = f (x, y) dengan (x, y) ∈ R dan n menyatakan
vektor normal satuan ke atas pada S. Jika f memiliki
turunan-turunan parsial pertama yang kontinu dan
F = M i + N j + P k suatu medan vektor kontinu, maka
∬ F ⋅ n dA = ∬ [−M fx − N fy + P ] dydx.
S
R
Supama dan Hadrian
Integral Permukaan
Integral Permukaan Fungsi Bernilai Real
Penghitungan Integral Permukaan
Contoh Soal
Contoh
1 Diketahui S merupakan suatu permukaan yang
didefinisikan oleh x2 + y 2 + z 2 = 4, z ≥ 1. Tentukan nilai
2
2
∬ (x + y )z dA.
S
2
Diketahui F = xi + yj + zk, S merupakaan permukaan
paraboloida z = 1 − x2 − y 2 yang terletak di atas bidang−xy,
dan n merupakan vektor normal satuan ke atas dari S.
Tentukan nilai
∬ F ⋅ n dA.
S
Supama dan Hadrian
Integral Permukaan