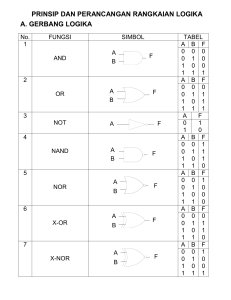
Gerbang logika

Gerbang logika ( Gate )
Gerbang logika atau gerbang logik adalah suatu entitas dalam elektronika dan
matematika Boolean yang mengubah satu atau beberapa masukan logik menjadi
sebuah sinyal keluaran logik.
Gerbang logika terutama diimplementasikan secara elektronis menggunakan
dioda atau transistor, akan tetapi dapat pula dibangun menggunakan susunan
komponen-komponen yang memanfaatkan sifat-sifat elektromagnetik (relay),
cairan, optik dan bahkan mekanik.
Jenis-jenis gerbang logika
Nama
Fungsi
Lambang dalam rangkaian
IEC 6061712
US-Norm
Tabel
kebenaran
DIN 40700
(sebelum
1976)
GerbangAND
(AND)
A
0
0
1
1
B
0
1
0
1
Y
0
0
0
1
Gerbang-OR
(OR)
A
0
0
1
1
B
0
1
0
1
Y
0
1
1
1
GerbangNOT
(NOT,
Gerbangkomplemen,
Pembalik(Inv
erter))
GerbangNAND
(Not-AND)
A
0
1
A
0
0
1
1
Y
1
0
B
0
1
0
1
Y
1
1
1
0
GerbangNOR
(Not-OR)
A
0
0
1
1
B
0
1
0
1
Y
1
0
0
0
GerbangXOR
(Antivalen,
ExclusiveOR)
atau
A
0
0
1
1
B
0
1
0
1
Y
0
1
1
0
atau
A
0
0
1
1
B
0
1
0
1
Y
1
0
0
1
GerbangXNOR
(Ekuivalen,
NotExclusiveOR)
Urutan tautology dalam penyederhanaan rangkaian logika :
[( ), -], [ ^, v], [-^, -v] , [,
-]
Contoh ekspresi beberapa operator yang telah menjadi suatu rangkaian :
Gambarlah gate dan buat tabel kebenaran dari fungsi Boolean berikut ini :
a.
Y=(A+BC’)
b. A= X.Y+(W’  Z )
c. F= ( A  B )’ + AC
d. F=X’(YZ)+WY’
RANGKAIAN (GERBANG) LOGIKA
Terbagi 2 yaitu :
1. KOMBINASIONAL
2. SEKUENSIAL
1. RANGKAIAN LOGIKA KOMBINASIONAL :
Outputnya bergantung pada keadaan nilai input pada saat
itu saja.
Piranti : Rangkaian gerbang OR - AND - NOT,
adder,subtractor dan multiplexer.
RANGKAIAN ADDER :
ADDER adalah rangkaian penjumlah, terdiri dari :
HALF ADDER (2-bit)
Simbol logika :
FULL ADDER (2-bit)
Simbol logika :
Rangkaian Logika :
Rangkaian Logika :
2. RANGKAIAN LOGIKA SEKUENSIAL
Outputnya tidak hanya bergantung pada nilai input saat itu,
tetapi juga input-input sebelumnya (karakteristik memori).
Piranti : Flip-flop, register, dan counter.
Berdasarkan waktu sinyal, dibedakan menjadi :
• Rangkaian sekuensial sinkron
Operasinya disinkronkan dengan pulsa waktu yang
dihasilkan oleh pembangkit pulsa yang merupakan masukan
bagi rangkaian.
Keluaran akan berubah hanya setiap adanya masukan pulsa
waktu, meskipun inputnya tidak berubah.
• Rangkaian sekuensial asinkron:
Operasinya hanya bergantung pada input, dan dapat
dipengaruhi setiap waktu.
PENYEDERHANAAN RANGKAIAN LOGIKA
Pada dasarnya rangkaian logika (digital) yang dibentuk dari beberapa
gabungan komponen elektronik yang terdiri dari bermacam-macam Gate dan
rangkaian-rangkaian lainnya, sehingga membentuk rangkaian elektronika
yang bersifatnya kompleks dan cukup rumit. Untuk mengatasi hal tersebut
maka dipergunakanlah beberapa metode penyederhanaan rangkaian logika.
Dalam penyederhanaan rangkaian logika, dapat menggunakan beberapa cara,
diantaranya :
1. Metode Aljabar Boolean
2. Metode Maksterm/Minterm( Kanonikal Form )
3. Metode Karnaugh Map
1 Aljabar Boole
Aljabar Boole mendefinisikan aturan-aturan untuk memanipulasi ekspresi simbol
logika biner. Ekspresi Logika simbol biner terdiri dari variabel biner dan operator.Nilai-nilai dari ekspresi
Boolean dapat ditabulasikan dalam tabel kebenaran [truth table].
Hukum-hukum Aljabar Boolean
1. Hukum identitas:
(i) a + 0 = a
(ii) a  1 = a
2. Hukum idempoten:
(i) a + a = a
(ii) a  a = a
3. Hukum komplemen:
(i) a + a’ = 1
(ii) aa’ = 0
4. Hukum dominansi:
(i) a  0 = 0
(ii) a + 1 = 1
5. Hukum involusi:
(i) (a’)’ = a
6. Hukum penyerapan:
(i) a + ab = a
(ii) a(a + b) = a
7. Hukum komutatif:
(i) a + b = b + a
(ii) ab = ba
8. Hukum asosiatif:
(i) a + (b + c) = (a + b) + c
(ii) a (b c) = (a b) c
9. Hukum distributif:
10. Hukum De Morgan:
(i) a + (b. c) = (a + b) (a +
(i) (a + b)’ = a’b’
c)
(ii) (ab)’ = a’ + b’
(ii) a (b + c) = a b + a c
11. Hukum 0/1
(i) 0’ = 1
(ii) 1’ = 0
Nb: Hukum aljabar Boolean diatas dapat
KEBENARAN
Contoh : Hukum penyerapan ( hk. No.6 )
dibuktikan
dengan
TABEL
Contoh 7.3. Buktikan (i) a + (a’b) = a + b
Penyelesaian:
a. (i) a + (a’b) = (a + ab) + a’b
(Penyerapan)
= a + (ab + a’b)
(Asosiatif)
= a + (a + a’)b
(Distributif)
=a+1b
(Komplemen)
=a+b
(Identitas)
b. Buat tabel kebenaran dan gatenya.
2.Sederhanakan A . (A . B + C)
Penyelesaian
A . (A . B + C)= A . A . B + A . C
=A.B+A.C
= A . (B + C)
(T6ii)
(T4b)
(T3a)
b. Buat tabel kebenaran dan gatenya
3. Sederhanakan A’. B + A . B + A’. B’
Penyelesaian
A’. B + A . B + A’. B’= (A’+ A) . B + A’. B’
= 1 . B + A’. B’
= B + A’. B’
= (B+A’)(B+B’) =( B+A’).1
(T3a)
(T8a)
(T7b)
= B + A’
(T9a)
b. Buat tabel kebenaran dan gatenya
4. Sederhanakan A + A . B’+ A’. B
Penyelesaian
A + A . B’+ A’. B= (A + A . B’) + A’. B
= A + A’. B
=A+B
(T6a)
(T9a)