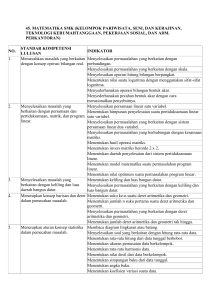
Rumus jumlah deret geometri tak hingga

BARISAN DAN DERET
AFLICH YUSNITA F, M.Pd.
STKIP SILIWANGI BANDUNG
1. Pola Bilangan
Adalah: susunan bilangan yang memiliki aturan atau pola tertentu
Contoh: 1,2,3,4,5…mempunyai pola bilangan ditambah satu dari
bilangan sebelumnya.
2. Barisan Aritmatika
Adalah: suatu barisan bilangan yang memiliki selisih dua suku
berurutan (beda) selalu tetap.
a, (a + b), (a + 2b), (a + 3b),…,(a + (n-1)b)
Suku ke- n ditentukan dengan rumus:
Un = a + (n-1)b
Dimana:
a = suku pertama
b = beda = Un - Un-1
INGAT!!!

Suku barisan adalah bilangan – bilangan
dalam suatu barisan.
suku pertama = U1
suku kedua = U2
suku ketiga = U3
……………………………………..
suku ke -n = Un
Contohnya :
1. 1, 3, 5, 7, …
U1 = 1
U2 = 3
U3= 5
U4 = 7
2.
5, 10, 15, 20, …
U1 = 5
U2 = 10
U3 = 15
U4 = 20
Rumus suku ke-n

+b
Misalnya suatu barisan aritmatika
mempunyai suku pertama a dan b. barisan
tersebut dapat dinyatakan sebagai berikut :
+b
a
+b
a+b
…
+b
a+2b
+b
a+3b
a+4b
Perhatikan :
U1 = a
U1 = a + (1 – 1 )b
U2 = a + b
U2 = a + (2 – 1 )b
U3 = a + 2b
U3 = a + (3 – 1 )b
U4 = a + 2b
U4 = a + (4 – 1 )b
U5 = a + 2b
U5 = a + (5 – 1 )b
Dari pola diatas didapatkan bahwa suku ke-n suatu
barisan aritmatika adalah Un = a + (n – 1 )b
Contoh soal……..
Tentukan suku pertama, beda, dan rumus suku
ke-n dari barisan aritmatika 3, 8, 13, 18, …
Jawab :
Suku pertama atau a = 3
Beda atau b = 5
Rumus suku ke-n = Un = a + (n – 1 )b
Un = 3 + (n – 1 )5
Un = 3 + (5n – 5 )
Un = 3 + 5n – 5
Un = 5n – 2
Pada suatu barisan aritmatika diketahui bahwa suku ke-2 adalah 0,dan suku ke-5 adalah 6
a.
Tentukan suku pertama dan beda dari barisan tersebut
b.
Tentukan rumus suku ke-n barisan tersebut
Jawab :
a.
U2 = 0
→a+b=0
….( 1 )
U5 = 6
→ a + 4b = 6 - ….( 2 )
-3b = -6
b=2
untuk b = 2 maka berdasarkan (1) dapat diperoleh a = -2
jadi, suku pertama dan beda barisan tersebut berturut – turut adalah a = -2 dan b = 2
b.
Berdasarkan hasil diatas diperoleh :
Un = a + (n – 1 )b
Un = -2 + ( n – 1 )2
Un = -2 + ( 2n – 2 )
Un = -2 + 2n – 2
Un = 2n – 4
jadi, rumus suku ke-n barissan tersebut adalah Un = 2n – 4
Sisipan
B.A = U1, U2, U3, . . . Un
Misalkan U1 = x
U2 = y
Dengan b = Un – U(n-1)

 suku awal

suku akhir
diantara U1 dan U2 disisipkan bilangan sebanyak
kx, ( x  b), ( x  2b),...( x  kb), y

k banyaksisipan
Sehingga didapat :
b = y - ( x + kb )
b = y – x – kb
kb + b = y – x
b(k+1)=y–x
yx
b = k 1
Setelah sisipan
Jadi beda barisan aritmetika yang terbentuk :
yx
k 1
Keterangan :
x = bilangan pertama
y = bilangan terakhir
k = banyak sisipan
b = beda
Contoh Soal :
1). Diantara 10 dan 13 disisipkan tiga bilangan sehingga
membentuk barisan aritmetika. Tentukan beda dari
barisan tersebut!
jawab :
x = 10
y = 13
k=3
b = yx
k 1
b=
13  10
3

3 1
4

Lanjutan jawaban :
B.A = 10,(10+b), (10+2b), (10+3b),13
=
=
3 

 3  
 3 
10, 10  , 10  2  , 10  3  ,13
4 

 4  
 4 
3
6
9
10,10 ,10 ,10 ,13
4
4
4
3
2
1
,11 ,12
,13
= 10,10
4
4
4
Deret Aritmatika

Pengertian :
Deret adalah jumlahan berurut
suku-suku dari suatu barisan
. Jumlah suku deret aritmatika
dinyatakan dengan Sn
Rumus Deret Aritamtika
• Bentuk umum
Sn 
n
 Uk  U1  U 2  U 3     U n
k 1
n
Sn   {a  k  1b a  a  b   a  2b   a  3b   ....  a  n  1b 
k 1
Bentuk umum deret aritamtika
Sn = U1 + U2 + U3 +
U4 +…+ Un atau
Sn = a+[ a+b] +[a+2b] +[a+3b]+…+[a+(n-1)b]
Rumus Deret Aritmatika
1
1
S n  na  U n   S n  n2a  n  1b
2
2






Sn = jumlah suku ke-n
a = U1 = suku pertama
b = (U2 – U1) = beda suku
n = banyak suku
Un = suku ke-n dengan
Un = [a + ( n – 1 ) b ]
Contoh : 1

Seorang pembuat sumur dengan ketentuan
biaya penggalian sebagai berikut:
1 m pertama biayanya Rp30.000,00
1 m kedua biayanya bertambah Rp5.000,00
1 m ketiga biayanya bertambah Rp5.000,00
demikian seterusnya, jika biaya penggalian
seluruhnya habis Rp525.000,00 maka
tentukan dalamnya sumur tersebut
Diketahui :
a = 30.000
b = 5.000
Sn= 525.000
Ditanyakan: n
Jawab :
Sn = n/2 {2a + (n – 1)b}
525.000 = n/2 {2(30.000) + (n – 1) 5.000}
525.000 = n/2 {60.000 + 5.000n – 5.000}
1.050.000 = 55.000n + 5.000n2
n2 + 11n – 210 = 0
(n +21) (n – 10) = 0
n = -21 atau n = 10
Jadi dalamnya sumur itu adalah 10 m.
BARISAN DAN
DERET GEOMETRI
Barisan Geometri

Barisan geometri adalah suatu barisan bilangan yang
memiliki perbandingan(rasio) antara dua buah suku
terdekat berturut-turut selalu tetap.
Contoh :
Barisan geometri
1. 1, 3, 9, 27, ...
2. 3, 6, 10, 25, …
Tentukan rasio dari masing-masing contoh di
atas dan apakah merupakan barisan geometri?
Contoh 1 :
1, 3, 9, 27, ...
rasio :
3 9
  ...  3
1 3
1, 3, 9, 27, ...merupakan barisan geometri karena
mempunyai perbandingan(rasio)tetap yaitu 3.
Contoh 2 :
3, 6, 10, 25, …
rasio : 6  10  ...
3
6
3, 6, 10, 25, …bukan merupakan barisan geometri
karena perbandingan(rasio)tidak tetap.
Rumus barisan geometri
Rumus suku ke-n dari barisan geometri adalah
U n  ar
dengan
Keterangan : Un = suku ke-n
a = suku pertama
n = banyaknya suku
r = rasio
n 1
Contoh :
Tentukan suku ke 8 dari barisan geometri berikut
2, 6, 18, 54, …!
Jawab :
Barisan geometri 2, 6, 18, 54, …
a2
6
r 
3
2
r 3
U n  a.r n 1
U 8  2(3) 7  2 x 2187  4374
Deret Geometri
Deret Geometri adalah jumlah suku-suku barisan geometri.
Jika barisan geometrinya adalah
maka deret geometrinya adalah
Bentuk ini dikenal sebagai jumlah n suku pertama
deret geometri,
yang dapat dinyatakan n, a, dan r.
Untuk itu, gunakan sifat bahwa rasio antara dua
suku berurutan selalu r dengan proses berikut.
Kita tuliskan hasil ini dalam teorema berikut tentang
suku ke-n dan jumlah n suku pertama deret geometri.
Teorema
Suku ke-n dan jumlah n suku pertama deret geometri
Pada deret geometri
dengan suku pertama =
dengan
= a dan rasio deret = r,
maka suku ke-n deret ini adalah
dan jumlah n suku pertamanya adalah
Contoh

Pada suatu deret geometri, jika suku
pertamanya adalah 7, suku terakhirnya
adalah 448 dan jumlahnya 889, tentukan
rasio dan banyaknya suku deret tersebut.
Jawab:
Jika deretnya S n  u1  u2  ...  un maka kita mempunyai
u1  a  7, u n  7r
n 1
 448, dan
1 rn
S n  7.
 889
1 r
Sn
1 rn
 7.
 889
1 r
dan
dari 7 r n 1  448 diperoleh r n1  64,
sehingga r n  64.r
Gantikan data ini pada persamaan terakhir
diperoleh
1  64r
7.
 889
1 r
1  64r
 127
1 r
1  64r  127  127r
63r  126
r2
Gantikan r = 2 ke persamaan
2 n  128  2 7
sehingga
n7
Jadi rasio deret adalah 2 dan
banyaknya suku deret adalah 7
r n  64r ,
Deret Geometri konvergen
( tak hingga )
Deret geometri tak hingga adalah
penjumlahan dari suatu deret geometri
yang jika deret tersebut kita
jumlahkan,maka kita tidak dapat
menghitung banyak seluruh deret
geometri tersebut. Atau dapat kita
tuliskan :
U1 + U2 + U3 + …..
contoh :
1 + 2 + 4 + 8 + …..
Jika suatu deret geometri tak hingga
dapat ditentukan pendekatan
jumlahnya, maka deret tersebut
dinamakan deret yang konvergen.
Contoh :
a. 1000 + 100 + 10 + 1 + 0.1 + …..
b. 100 – 50 + 25 – 12½ + …..
Rasio masing - masing deret tersebut
adalah 0.1dan -½
Suatu deret geometri tak hingga
mempunyai jumlah tertentu
(konvergen) jika rasio deret tersebut
terletak pada interval
-1< r < 1 atau |r| < 1
Rumus jumlah deret geometri tak
hingga
Jumlah n suku pertama deret geometri
dengan suku pertama a dan rasio r
adalah :
a
S 
1 r
Contoh 1 :
Carilah jumlah deret geometri berikut.
4
36  12  4   .....
3
Jawab :
1
r
a  36
3
sehingga, S  a
1 r
36
36
S 

 27
 1  4
1    
 3  3
Contoh 2 :
Diketahui jumlah tak hingga 4 dan rasionya ½, maka
tentukanlah suku pertamanya !
Jawab :
1
Sehingga,
S  4 r 
a
2
S 
1 r
a
4
1
1
2
a
4
1
2
a  4.
Jadi suku pertamanya adalah 2
1
2
2
Soal
1. Carilah jumlah deret geometri berikut
1
4  2  1   .....
2
2. Diketahui jumlah tak hingga 4 dan suku
pertamanya 16, maka tentukanlah
rasionya !
Deret Geometri tak terhingga
Deret geometri tak hingga adalah deret
geometri dengan |r| < 1.
Jumlah S dari dert geometri tak hingga
adalah
a1  0 
a
s 


1 r
1 r
Rumus pada deret geometri berlaku juga
untuk n tak terhingga. Adapun untuk n tak
terhingga terdapat dua kasus yang harus
kalian perhatikan, yaitu:
Kasus
Jika r < -1 atau r > 1, maka untuk n →∞,
nilai rn makin besar.
Untuk r < -1, n →∞, dengan n ganjil
didapat rn →∞
Untuk r < -1, →∞, dengan n genap
didapat rn →∞
Untuk r > 1, rn →∞ didapat rn →∞
a1   
Akibatnya,
s 
1 r
 
Deret geometri dengan r < -1 atau r > 1 ini
disebut deret geometri divergen
(memencar).
Contoh 1 :
Suatu deret geometri mempunyai suku ke5 sama dengan 64 dan suku ke-2 sama
dengan 8. Tentukanlah jumlah 10 suku
pertama dan jumlah n suku pertama deret
geometri tersebut!
Jawab:
u2  8, berarti : ar  8
u5  64, berarti : ar 4  64
ar.r 3  64
8r 3  64
r3  8
Sehingga didapat r = 2
Dengan mensubstitusi r = 2 ke persamaan
ar = 8, kalian mendapatkan a.2 = 8 sehingga
a=4
Jumlah n suku pertama deret ini adalah :


4 1 2
4  4.2
Sn 

1 2
1
n
2 n
 4.2  4  2 .2  4
2
2 n
n
4
n
Jumlah 10 suku pertama deret ini adalah :
S10  2
2 10
4
 212  4
 4.096  4
 4.092
Sebuah bola basket dijatuhkan dari ketinggian
6 m. pada setiap pantulan, bola memantul dan
mencapai ketinggian dari ketinggian semula.
Tentukan panjang lintasan yang terjadi
hinggabola benar-benar berhenti.
Jawab
Panjang lintasan total bola hingga berhenti dinyatakan
oleh deret berikut
S   h0  2h1  h2  ...
h0= ketinggian mulamula 6 m.
2
2
h1  h0   6  4m
3
3
2
2
2 2
4
24
2
h2  h1  . h0    h0   6 
m
3
3 3 2 3 3 9
9
2
2 2
8
2
h3  h2  .  h0    h0 
m
3
3 3
27
3
2
hn  hn 1
3
Dengan demikian, anda dapat menuliskan
2
2

2


S   h0  2h1  h2  h3  ...  hn   6  2 6    6  ...
3

3


  2   2 2


 6  2 4   4    4  ...
 3 3



Dapat anda lihat bahwa:
2
2 2
4   4    4  ....
3 3
Merupakan deret geometri tak hingga konvergen dengan
a = 4 dan r =2/3 .Oleh karena itu, jumlah dari deret tersebut
(dimisalkan D) adalah
a
D

1 r
4
4
  12
2 1
1
3 3
Dengan demikian:
S  6  2 D
 6  2(12)
 30
Jadi, panjang lintasan yang dilalui bola sampai
bola berhenti adalah 30 m.