BAB V SEMIKONDUKTOR Isolator, Semikonduktor

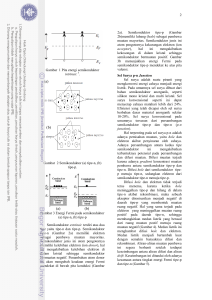
Bab V, Semikonduktor
Hal: 119
BAB V
SEMIKONDUKTOR
Isolator, Semikonduktor dan Konduktor
Secara sederhana zat padat dapat dikelompokkan sebagai Isolator,
Semikonduktor dan Konduktor. Bahan semikonduktor adalah suatu
material dengan sifat konduktivitas diantara konduktor dan isolator,
contoh Silikon (Si), Ge (Germanium). Saat ini Si umumnya
digunakan sebagai devais elektronik, seperti dioda, transistor, IC
(integrated circuit) namun GaAs memiliki potensi yang besar untuk
digunakan sebagai devais elektronika pada masa datang, terutama
ditujukan untuk beroperasi pada frekuensi tinggi.
Untuk menjelaskan konduktivitas bahan sering kali menggunakan
konsep pita energi. Ada dua pita energi, yaitu pita valensi dan pita
konduksi. Pita valensi adalah pita energi yang mungkin diisi oleh
elektron dari zat padat hingga komplit. Setiap pita memiliki 2N
elektron dengan N adalah jumlah atom. Bila masih ada elektron yang
tersisa akan mengisi pita konduksi. Pada suhu 0 K, pita konduksi
terisi sebagian untuk bahan konduktor, sedangkan untuk isolator dan
semikonduktor tidak ada elektron yang mengisi pita konduksi.
Perbedaannya terletak pada energi gap Eg yaitu selang energi antara
pita konduksi minimum dan pita valensi maksimum. Pada bahan
semikonduktor Eg ~ 1 eV, sedang pada isolator Eg ~ 6 eV. Secara
diagramatik pita energi dari isolator, semikonduktor dan konduktor
ditunjukkan pada gambar berikut.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
pita konduksi
minimum
pita valensi
maksimum
Hal: 120
pita konduksi
minimum
pita valensi
maksimum
pita valensi
maksimum
pita konduksi
minimum
ISOLATOR
SEMIKONDUKTOR
KONDUKTOR
(a)
(b)
(c)
Gambar 1, Perbedaan tingkat energi dari material
Gambar (a) Æ Struktur pita energi isolator (misal intan).
Pita larangan yang besar ini memisahkan pita valensi
yang terisi dengan pita konduksi yang kosong.
Gambar (b) Æ Struktur pita energi semikonduktor (misal grafit).
Lebar pita relatif kecil, Eg ≈ 1 eV. Pada saat suhu
naik, elektron pada pita valensi mampu berpindah ke
pita konduksi. Karena adanya elektron di pita
konduksi akibatnya bahan itu menjadi sedikit
konduktif, karena itu disebut semikonduktor.
Gambar (c) Æ Struktur pita energi konduktor (misal metal).
Pita konduksi terisi sebagian, jika ada medan listrik
luar elektron akan memperoleh tambahan energi
sehingga berpindah yang berakibat timbul arus
listrik.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 121
Teorema Pita Energi Kristal
Dalam sistem susunan berkala unsur-unsur, atom Si termasuk
golongan IV, jadi ada 4 elektron pada orbit terluarnya. Masingmasing atom Si membentuk struktur kristal dengan atom-atom
tetangganya dan elektron-elektron valensinya membentuk ikatan
kovalen, sehingga masing-maing atom seolah-olah memiliki 8
elektron terluar dengan 4 elektron berasal dari miliknya sendiri
sedang 4 elektron lainnya berasal dari 4 atom tetangga terdekatnya.
Susunan ini membentuk kristal silikon intrinsik dengan muatan total =
0 coulomb, sketsa kristal Si ditunjukkan pada gambar berikut.
-
-
-
-
-
-
-
+
-
-
+
-
-
-
-
+
-
-
+
-
-
-
-
+
-
+
-
+
-
+
+
+
Gambar 2, Sketsa kristal Si
Kristal intrinsik ini bervibrasi akibat energi termal yang memberikan
energi tambahan pada kristal instrinsik tsb. Energi ini tidak
terdistribusi secara merata sehingga pada beberapa titik kisi akan
pecah demikian pula elektronnya akan lepas dari ikatannya sehingga
menjadi elektron bebas yang akan menjadi pembawa muatan negatif.
Sebaliknya titik dimana elektron tsb meninggalkan tempatnya
menjadi bermuatan positif dan dikenal sebagai hole, yang membawa
muatan positif.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 122
Bila diberi sumber DC akan ada arus listrik yaing mengalir di dalam
kristal tsb. Elektron akan bergerak ke kutub positif sumber DC tsb
sedangkan hole akan bergerak berlawanan arah.
Mobilitas dan Konduktivitas
Arus listrik pada metal terjadi akibat perpindahan elektron, sedang
pada semikonduktor bergantung pada elektron dan hole.
Semikonduktor dapat di-dope menjadi:
a. dominan hole
Æ tipe-p
b. dominan elektron Æ tipe-n
Hal ini berarti bahwa semikonduktor tipe-n memiliki jumlah elektron
bebas lebih banyak dibandingkan dengan jumlah hole dan sebaliknya
untuk tipe-p jumlah hole lebih banyak dari jumlah. Karena itu
elektron pada tipe-n disebut pembawa muatan mayoritas dan hole
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 123
adalah pembawa muatan minoritas, sebaliknya pada tipe-p elektron
adalah pembawa muatan minoritas sedangkan hole adalah pembawa
muatan mayoritas.
Semikonduktor Instrinsik
Pada suhu 0 K, kristal Si atau Ge berkelakuan sebagai isolator, sedang
pada suhu kamar T, beberapa ikatan kovalen putus akibat energi
termal (Eg = 0,72 eV untuk Ge dan 1,1 eV untuk Si), akibatnya ada
elektron bebas dalam kristal dan ada hole yang ditinggalkan oleh
elektron akibat terputusnya ikatan kovalen tsb, seperti diilustrasikan
sbb:
Untuk semikonduktor intrinsik (murni) konsentrasi elektron bebas dan
konsentrasi hole-nya sama, atau:
n = p = ni
dengan ni : konsentrasi instrinsik.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 124
Untuk memperbesar konduktivitas, bahan semikonduktor itu diberi
doping, akibatnya bahan itu itu akan menjadi tipe-n atau tipe-p
tergantung doping-nya, sehingga menjadi semikonduktor ekstrinsik.
Dopan dikelompokkan sebagai:
a. donor Æ diberi impuritas yang bervalensi +5 (misalnya P, As,
Sb) Æ tipe-n
b. akseptor Æ diberi impuritas yang bervalensi +3 (misalnya Bo,
In, Ga, B) Æ tipe-p
Konsentrasi doping ~ 1 ppm. Dengan adanya doping maka akan
berakibat n ≠ p, sehingga konduktivitasnya menjadi :
untuk tipe-n
σ d = nqμn
untuk tipe-p
σ a = pq μ p
dengan n dan p adalah masing-masing konsentrasi impuritas untuk
donor dan akseptor.
Pada saat pemberian impuritas donor (tipe-n) akan muncul tingkat
energi yang diperbolehkan di bawah energi pita konduksi terendah
yaitu sekitar ≈ 0,01 eV (untuk Ge) dan ≈ 0,05 eV (untuk Si). Sehingga
pada suhu kamar hampir semua elektron donor berada di pita
konduksi.
Untuk impuritas akseptor (tipe-p) juga akan muncul tingkat energi di
atas tingkat energi pita valensi tertinggi. Karena hanya perlu energi
kecil saja elektron dari pita valensi berpindah ke tingkat energi
akseptor akibatnya akan timbul hole di pita valensi.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 125
dikotori dengan Sb
dikotori dengan In
Untuk kesetimbangan termal berlaku hukum mass-action, yaitu:
n × p = ni2
Æ Hasil kali konsentrasi hole dengan elektron tidak bergantung pada
konsentrasi donor maupun akseptor tanpa memperhatikan level
dopingnya.
Jika ada donor, maka donor akan terionisasi sehingga rapat muatan
menjadi = ND +p. Sedang untuk akseptor juga akan terionisasi,
sehingga rapat muatan menjadi = NA + n. Karena semikonduktor
dalam keadaan netral, akibatnya:
ND +p = NA + n.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Untuk :
dengan:
Hal: 126
ni2
tipe-n Æ N A =0 → n n ≈ N D → p n =
ND
ni2
tipe-p Æ N D =0 → p n ≈ N A → n p =
NA
nn, pn : konsentrasi elektron mobile, dan hole pada tipe-n
np, pp : konsentrasi elektron mobile, dan hole pada tipe-p
nn pn = ni2
np pp = ni2
NA dan ND adalah konsentrasi hole dan elektron inmobile
elektron: pembawa muatan mayoritas pada tipe-n, dan
pembawa muatan minoritas pada tipe-p
hole:
pembawa muatan mayoritas pada tipe-p, dan
pembawa muatan minoritas pada tipe-n.
Contoh untuk tipe-p, berlaku N D = 0 diperoleh :
ni 2
p + ND = p = n + N A =
n
atau n 2 + N A n − ni2 = 0 , didapat : n = 12 (− N A + N A 2 + 4ni 2 )
Untuk tipe-n (NA = 0), didapat : p = 12 (− N D + N D 2 + 4ni 2 )
Sifat-sifat listrik dari Ge dan Si
Metal bersifat unipolar Æ arus listrik hanya berasal dari perpindahan
elektron saja. Sedangkan Semikonduktor bersifat bipolar Æ ada dua
pembawa muatan (elektron Æ pembawa negatif, hole Æ pembawa
positif).
Pada saat bahan semikonduktor diberi medan listrik E Æ timbul arus,
dengan
J = (nμ n + pμ p ) q E = σ E
n : konsentrasi elektron bebas
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 127
p : konsentrasi hole
σ : konduktivitas
σ = (n μn + p μp) q
n = p = ni Æ untuk semikonduktor intrinsik
Konsentrasi intrinsik bergantung pada suhu yang dinyatakan sebagai:
3 −
n i = AoT e
2
dengan
E Go
kT
Ao : konstanta
EGo : energi gap pada T = 0 K
k : konstanta Boltzman.
Secara eksperimental energi gap bergantung pada suhu, sebagai:
untuk Si:
1,21 – 3,60 x 10-4 T
untuk Ge:
0,785 – 2,23 x 10-4 T
EG = 1,1 eV (Si) dan 0,72 eV (Ge)
Pada suhu ruang
Mobilitas μ ternyata bergantung pada suhu dan medan listrik, sebagai:
μ ÷ T-m
untuk
Si,
m = 2,5 untuk elektron
m = 2,7 untuk hole
untuk
Ge, m = 1,66 untuk elektron
m = 2,33 untuk hole
Jika E < 103 V/cm
Æ μ bukan fungsi E
103 < E < 104 V/cm
Æ μ ÷ E-1/2
E > 104 V/m
Æμ÷E
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 128
Difusi
Konsentrasi pembawa muatan dapat tidak homogen, seperti pada
gambar.
Ketidak homogen-an konsentrasi hole ini mengakibatkan arus difusi,
yang dinyatakan sebagai :
J p = −q D p
dengan
dp
dx
Dp : konstanta difusi untuk hole
tanda minus karena dp/dx negatif untuk x positif.
Difusi dan mobilitas saling dependen, sesuai dengan relasi Einstein:
Dp
Dn
=
μn
μp
= VT =
kT
q
Pada semikonduktor gradien potensial dan gradien konsentrasi dapat
terjadi bersama-sama, sehingga arus yang mengalir merupakan
kombinasi karena drift dan difusi, sebagai:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 129
dp
dx
dn
J n = q μ n n E + q Dn
dx
J p = q μ p p E − q Dp
(A)
(B)
Persamaan Kontinuitas
Secara umum konsentrasi pembawa muatan sebagai fungsi dari posisi
dan waktu, namun perlu diingat bahwa muatan tidak dapat diciptakan
atau dimusnahkan, berlaku:
dengan
∂p p o − p 1 ∂J p
=
−
τp
q ∂x
∂t
(C)
∂n n o − n 1 ∂J n
=
−
τn
q ∂x
∂t
(D)
index p dan n masing-masing untuk hole dan elektron,
τ : mean lifetime,
po dan no : nilai p dan n pada saat kesimbangan termal,
J : rapat arus
Medan listrik E berkaitan dengan rapat muatan sesuai dengan
persamaan Poisson:
ρ
q
∂E
=
= ( p + ND − n − NA )
ε
ε
∂x
dengan
(E)
ε : permitivitas bahan semikonduktor
ND : konsentrasi donor
NA : konsentrasi akseptor
Dari kelima persamaan ini dapat dicari hubungan antara besaranbesaran p, n, E, Jp dan Jn.
Untuk bahan tipe-n, persamaan di atas diberi indeks n, persamaan
kontinuitas menjadi:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 130
∂p n p n o − p n
∂ (p n E)
∂ 2pn
=
− μp
+ Dp
.
τp
∂t
∂x
∂x 2
Persamaan ini sukar diselesaikan, ambil kasus khusus
1. Konsentrasi tak bergantung x (∂p/∂x = 0) dan E = 0
2. Konsentrasi tak bergantung t (∂p/∂t = 0) dan E = 0
3. Konsentrasi berubah secara sinusoida terhadap t dan E = 0
Dioda PN
Hubungan pn dapat terjadi dengan mendifusi impuritas tipe-p pada
salah satu ujung kristal tipe-n. Walaupun ada hubungan antara dua
tipe silikon namun sebagai keseluruhan bertidak sebagai kisi kristal
tunggal. Akibatnya elektron bebas dari tipe-n akan bergerak menuju
hole pada tipe-p demikian pula hole pada tipe-p bergerak ke elektron
di tipe-n sehingga terjadi proses rekombinasi. Selanjutnya akan terjadi
lapisan deplesi. Pada dasarnya lapisan ini adalah isolator dengan
kelebihan elektron di sisi tipe-p dan kelebihan hole di sisi tipe-n dan
berakibat timbulnya beda tegangan di hubungan pn, yaitu Vγ , seperti
ditunjukkan pada Gambar 3.
Setelah hubungan PN terbentuk, hole dari tipe-p konsentrasinya lebih
besar dari hole di tipe-n, sehingga hole akan berdifusi, demikian pula
pada elektron juga akan berdifusi dan ber-rekombinasi. Namun proses
ini tidak terjadi terus menerus dan akan berhenti jika terjadi
kesetimbangan antara difusi dan drift. Dalam keadaan seimbang:
1. daerah tipe-p netral
2. daerah muatan ruang tipe-p
3. daerah muatan ruang tipe-n
4. daerah tipe-n netral
Daerah (2) dan (3) Æ daerah muatan ruang/lapisan deplesi/dipole
listrik. Pada daerah ini ada medan listrik walaupun tidak diberi
tegangan.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 131
lapisan deplesi
-
p
+
+
+
+
+
+dp
-dp
n
V?
Gambar 3 Lapisan deplesi dan tegangan deplesi Vγ
Dalam keadaan seimbang, Jn = 0, sehingga: J n = q μ n n E + q D n
= 0. Diperoleh E = −
D n 1 dn
kT d
=−
( ln n )
μ n n dx
q dx
dn
dx
(Relasi Einstein
D n kT
)
=
μn
q
atau:
VB =
dn
∫
E dx =
− dp
VB =
dn
kT d
∫−d q dx ( ln n ) dx
p
kT n n kT n n n p
kT n A n D
ln =
ln 2 =
ln 2
q np
q
ni
q
ni
Jadi walaupun dalam keseimbangan termal, terdapat beda tegangan
antara antara kedua kutub dioda Æ tegangan difusi.
Model Pita pada dioda hubungan
Ada banyak cara untuk membuat dioda hubungan, diantaranya adalah
dengan step junction, yaitu distribusi muatan akseptor/donor secara
uniform. Pada saat dihubungkan tingkat energi Ferminya akan sama,
seperti ditunjukkan pada gambar berikut ini.
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 132
EC
?
EF
EV
?
Daerah tipe -p
Daerah tipe -n
Untuk 0 < x < dn:
Pers. Poisson :
q ND
q ND
dE
=
ÆE =
x + Cn
dx
ε
ε
E =
q ND
(x-d n )
ε
Untuk –dp < x < 0:
E = -
q NA
q NA
x + Cp Æ E = (x + d p )
ε
ε
dengan Cn dan Cp : konstanta integrasi, dicari dengan syarat batas.
Pada x = 0, E = Em dan E = 0 untuk x = -dp dan x = dn Æ Cn = Cp
q NAdp
q NDdn
dan Cn = Æ ND dn = NA dp.
Cp = ε
ε
Sedangkan potensial listrik diperoleh dari V = ∫ E dx
qN A d p 2
qN D 1 2
Untuk 0 < x < dn : V = −
( 2 x − d n x ) + 2ε
ε
qN A d p 2
qN A 1 2
Untuk – dp < x < 0: V =
( 2 x − d p x ) + 2ε
ε
q ( NAd p 2 + N Dd n 2 )
Pada x = dn
Æ V = VB =
2ε
Secara grafis ditunjukkan sbb:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 133
Hubungan antara energi elektron dengan tegangan elektrostatis
dinyatakan sebagai E = - qV. Sehingga model pita pada dioda
hubungan p-n sbb:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 134
Kapasitansi pada lapisan Deplesi
Pada lapisan deplesi terdapat muatan ppositif dan negatif, yang dapat
dianggap sebagai kapasitor, seperti ditunjukkan pada gambar berikut.
Dengan menganggap sebagai kapasitor plat sejajar, maka kapasitansi
dari dioda tsb adalah:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I
Bab V, Semikonduktor
Hal: 135
εA
εA
=
dn + dp
d
Kapasitansi ini dikenal sebagai kapasitansi deplesi (kapasitansi
hubungan)
C=
dengan memanfaatkan ND dn = NA dp dan VB =
q ( NAd p 2 + N Dd n 2 )
2ε
2ε VB ⎛ 1
1 ⎞
+
⎜
⎟ . Sebaliknya jika ada
q ⎝ NA ND ⎠
tegangan bias, maka persamaan ini nilai VB diganti dengan VB ± V,
dengan V tegangan bias yang diberikan ke dioda hubungan, sehingga
2ε ⎛ 1
1 ⎞
d=
+
⎜
⎟ ( VB ± V )
q ⎝ NA ND ⎠
Selanjutnya diperoleh:
εA
qε
=A
C=
⎛ 1
1 ⎞
2ε ⎛ 1
1 ⎞
+
2
+
⎜N
⎟ ( VB ± V )
( VB ± V )
⎜
⎟
N
q ⎝ NA ND ⎠
⎝ A
D ⎠
diperoleh d = dn + dp =
Secara grafis hubungan C-2 vs. V diberikan sbb:
Sastra Kusuma Wijaya
FISIKA FMIPA UI Diktat Kuliah Elektronika I