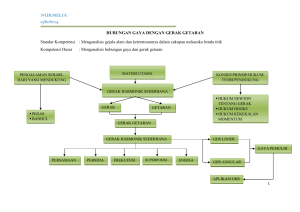
Gerak Harmonik Sederhana

Matakuliah
Tahun
: D0684 – FISIKA I
: 2008
OSILASI
Pertemuan - 22
1. Osilasi
Gerak Periodik : Gerak yang berulang dalam selang
waktu yang sama
Gerak Harmonik : Pergeseran partikel dapat dinyatakan
sebagai fungsi SINUS atau COSINUS
Osilasi / vibrasi : Gerak periodik dari partikel , yang
bolak -balik melalui lintasan yang
sama
Gerak Harmonik teredam : gerak bolak - balik partikel
tidak tepat sama, karena terdapat gaya
gesekan
3
Bina Nusantara
2. Gerak Harmonik Sederhana
- Variabel Gerak Osilasi
Periode (T) : Waktu yang diperlukan untuk 1 getaran .
satuan : detik
Frekuensi (f): banyaknya getaran per - satuan waktu.
satuan : cycle/s ( = Hz )
Frekuensi sudut () :  = 2 f ; satuan : rad/det
Amplitudo ( = A ): Simpangan maksimum.
satuan:satuan panjang: m/cm/mm
4
Bina Nusantara
- Gerak Harmonik Sederhana
Benda , massa m dan berada pada ujung sebuah
pegas , gaya yang diperlukan untuk
menyimpangkannya sejauh X adalah :
F=kX
k = konstanta pegas
Gaya reaksi oleh pegas :
F’ = - k X
gaya reaksi ini disebut : GAYA PEMULIH
Dalam setiap gerak harmonik, gaya pemulih inilah
yang menyebabkan benda berosilasi .
Bina Nusantara
Pada gerak harmonik sederhana, dianggap benda tidak
mengalami gaya gesekan.
Dari Hk. Newton II : F = m a = m d2X/dt2
dan gaya pemulih : F’ = - k X
maka :
-k X = m d2X/dt2
atau :
d2X/dt2 + ( k/m ) X = 0
Solusinya : X = A Cos (  t +  )
( Pers. Diff. G.H.S )
( Pers. GHS )
Dimana :  = √(k/m) = frekuensi sudut
 t +  = fasa gerak
 = konstanta fasa
A = amplitudo = simpangan maksimum benda berosilasi
A dan  ditentukan dari keadaan awal
Bina Nusantara
3. Energi Pada Gerak Harmonik Sederhana
* Kecepatan partikel berosilasi
V = dX/dt = - A  Sin( t +  )
Pada simpangan maksimum V = 0, karena kecepatan
berbalik arah
* Percepatan partikel berosilasi
a = dV/dt = - A 2 Cos( t +  )
di titik seimbang ( X=0) , F = 0 ; a = 0 ;
* Energi Kinetik :
EK = ½ m V2 = ½ k A2 Sin2 ( t +  )
Bina Nusantara
EKmaks. = ½ k A2
dan V = maks.
* Energi Potensial :
EP = ½ k X2 = ½ kA2 Cos2 ( t +  )
EPmaks. = ½ kA2
* Energi Total
Energi total setiap saat adalah :
EK+EP = ½ kA2Cos2( t +  ) + ½ k A2 Sin2( t+)
= ½ kA2 (Cos2( t + ) + Sin2 ( t +  ) ) = ½ kA2
Energi total dalam GHS adalah konstan , yaitu : ½ kA2
EKmaks = EPmaks = ½ k A2 = E
Bina Nusantara
4. Bandul
4.1. Bandul Matematis
Sebuah benda diikatkan pada ujung sebuah tali ringan,
dan ujung tali satu lagi dipakukan, hingga sistem
membentuk sebuah ayunan sederhana .
L = panjang tali

Benda disimpangkan sebesar  , dan
L
Dilepas hingga benda berayun disekitar
titik seimbangnya.
mg
Untuk simpangan sudut  kecil : sin  =  bandul akan
melakukan GHS , dengan frekuensi sudut :
 =  g / L dan periode : T = 2  L/g
Bina Nusantara
4.2. Bandul Fisis
Bandul berbentuk sebarang,
bermassa M ,
L = jarak sumbu putar (S)
ke pusat massa (C)
Torsi pemulih :  = - MgL sin
Untuk simpangan  kecil, bandul
akan melakukan GHS , dengan :
Periode :
T  2π
I
MgL
I = momen inersia bandul
Bina Nusantara
S

L
C
Mg
5. GERAK HARMONIK TEREDAM
Pada semua gerak osilasi energi mekanik total akan
berkurang karena adanya gesekan (redaman ) , hingga
suatu saat benda akan berhenti berosilasi. Gaya
redaman umumnya berbanding lurus dengan
kecepatan yaitu :
-bV = - b(dX/dt)
b = konstanta
gaya pemulih menjadi : -kX-b(dX/dt)
Maka :
2X
d
m 2  b dX  kX  0
dt
dt
Untuk b kecil solusinya adalah :
X = A e - bt/2m Cos ( ’t +  )
dengan : ’ = 2 f =  k/m- (b/2m)2
Bina Nusantara
 = 2m/b disebut umur osilasi rata-rata , dimana
amplitudo tinggal (1/e) dari amplitudo awal.
Karena amplitudo berkurang, berarti energi- nya
juga berkurang. Bila kehilangan energi per
periode adalah ∆E , didefiniskan faktor kualitas :
Q = 2π E / ‫∆׀‬E ‫׀‬
Dimana: E = energi total untuk 1 periode
Bina Nusantara