Scientific Echosounders

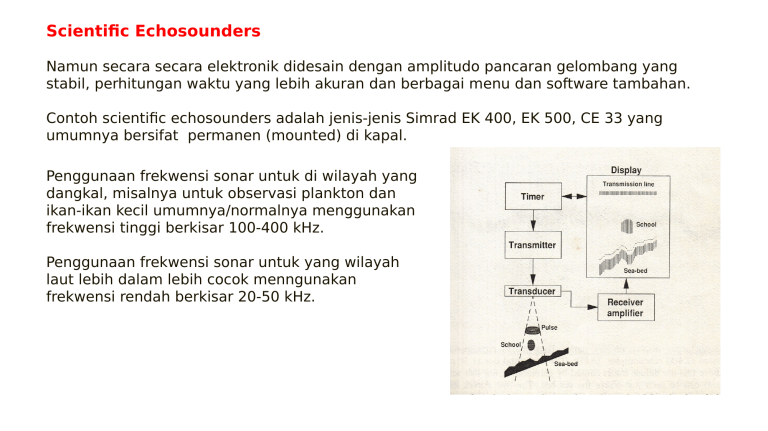
Scientific Echosounders
Namun secara secara elektronik didesain dengan amplitudo pancaran gelombang yang
stabil, perhitungan waktu yang lebih akuran dan berbagai menu dan software tambahan.
Contoh scientific echosounders adalah jenis-jenis Simrad EK 400, EK 500, CE 33 yang
umumnya bersifat permanen (mounted) di kapal.
Penggunaan frekwensi sonar untuk di wilayah yang
dangkal, misalnya untuk observasi plankton dan
ikan-ikan kecil umumnya/normalnya menggunakan
frekwensi tinggi berkisar 100-400 kHz.
Penggunaan frekwensi sonar untuk yang wilayah
laut lebih dalam lebih cocok menngunakan
frekwensi rendah berkisar 20-50 kHz.
● Kegunaan
- Menentukan kedalaman perairan
- Menentukan karakteristik jenis dasar perairan
- Menentukan keberadaan obyek bawah air, misal
ikan
- Menentukan kelimpahan ikan
- Menentukan ukuran ikan, untuk seleksi
penangkapan
Kegunaan echosounder menjadi lebih banyak karena
dikombinasikan GPS dan digital thermometer, sehingga
disamping bisa menentukan 5 hal di atas, juga bisa
untuk menentukan temperatur air, posisi sampling,
kecepatan dan arah perjalanan sampling.
Penggunaan Frekwensi Sonar
Banyak pilihan:
1. 38 kHz (38000 cycles per second)
2. 40 kHz
15ᵒ
3. 50 k Hz 46ᵒ
4. 120 kHz
5. 200 kHz 10˚
6. 400 kHz 5˚
Lebar dari sudut pancaran sonar proporsional dengan
frekwensi bunyi yang digunakan, sebagai contoh: 400
kHz sudut pancaran 5˚, 40 kHz sudut pancaran 15˚.
Tabel 1. Kelebihan dan kekurangan antara 2 jenis frekwensi yang
dihasilkan oleh tranduser dalam proses sounding
No
Karakteristik
50 kHz
200 kHz
1. Lebar lengan pancaran
46º
2. Resolusi
tinggi
rendah
3. Pengaruh gelembung
bisa
udara dan suara kapal
4. Pengaruh gerak naik
turun kapal
10º
kurang bisa
diminimalisir
kurang
berpengaruh
pd tampilan
kontur dasar
diminimalisir
berpengaruh
pd tampilan
kontur dasar
Prinsip Kerja
● Gelombang ultrasonik dipancarkan ke dalam air dengan
kecepatan konstan.
● Ketika gelombang bunyi mengenai obyek bawah air, sebagian
gelombang bunyi akan dipantulkan balik ke sumber bunyi.
● Dengan cara mengitung perbedaan waktu antara pemancaran
gelombang bunyi dan penerimaan gelombang bunyi yang
dipantulkan maka kedalaman obyek dapat ditentukan.
Dimana d = kedalaman
c = Kecepatan bunyi dalam air
Δt = selang waktu
2. FORMULASI KECEPATAN BUNYI
Menurut Caruther (1977) persamaan kecepatan bunyi
di laut dapat diturunkan dari persamaan gelombang:
1
 P 2
C
2
  P

 0
2 
 t 
2
P
: Tekanan
C
: Kecepatan bunyi
: Operator lapalace
t
: Waktu
(2.1)
Dimana
● Bentuk kelengkungan arah pembelokan bunyi,
ditentukan dengan gradien kcepatannya
C
g
D
Keterangan:
g
C
D
: Gradien kecepatan (4.3)
bunyi
: Selisih kecepatan bunyi pada
kedalaman D (CD ) dengan
C0
CD
: selisih kedalaman pada
C0
dan
●
Untuk gradien kecepatan bunyi konstan maka
rambat gelombang berupa busur lingkaran yang
pusatnya
terletak
pada
kedalaman
dimana
kecepatan bunyi nol ( Kisler et al, 1980), maka
diperoleh:
C
R
gCos
g = gradien kecepatan bunyi
R = jari-jari kelengkungan kurva arah rambat
gelombang
Θ = sudut depresi
●
Gradien kecepatan bunyi akan negatif, jika jari-jari
kelengkungan kurva pasitif, sehingga rambat gelombang akan
sibelokkan ke bawah.
● Untuk gradien kecepatan bunyi positif, maka jari-jari
kelengkungan kurva negatif sehingga rambat gelombang akan
dibelokkan ke atas.
2. Attenuasi daya karena refleksi di
dasar laut
● Apabila terjadi refleksi di dasar laut,
maka
atenuasi daya rambat gelombang
akustik B1 Z 2 Z1 sin  i  sin  t
R

Z 2 dari
dapat dihitung
sin  koefisien
sin 
A1
Z1
i
t
refleksi:




B1,A1
berturut-turut
menyatakan
amplitudo gelombang yang direfleksikan
dan yang datang, Z2/Z1 menyatakan
perbandingan impedansi dasar laut dan
air laut. Z2 bergantung pada jenis dasar
laut, apakah terdiri dari Lumpur, pasir,
kerikil
atau
batu.
Kehilangan
daya
● Atenuasi dapat dirumuskan :

b
 20 log 10 R
Bila suara tersebut datang tegak lurus,
maka i=t=90˚. Kalau Z2/Z1 =2.4
(untuk dasar pasir), maka :
2,4  1
R
 0.4118 dan
2,4  1

S
 20 log 10 .0.4118  7.778
●.2 GELOMBANG BUNYI
2
Kecepatan gelombang bunyi di air berkisar 1450-1550
m/s, tergantung dari temperatur, tekanan dan salinitas.
Formulasi:
C  f
Semakin pendek panjang gelombang, atau semakin tinggi
frekuensi, semakin mudah untuk membedakan sasaran yang
berdekatan.
Jika C: 1500 m/s, jika frekwensi yang digunakan 10 kHz
maka panjang gelombang 15 cm.
Jika frekwensi 500 kHz, maka panjang gelombangnya 3
mm.
P=pcv
Gambar 2.1. Gelombang Bunyi
P: Tekanan
ρ : Densitas air
C: Kecepatan bunyi dalam air
V : Kecepatan partikel kaitannya dengan kecepatan bunyi
Lebar band tergantung dari durasi pulsa
Semakin pendek pulsa, maka semakin besar spektrum dari frekwensi
yang ditranmisikan oleh sonar.
Contoh: jika durasi pulsa
ms, maka lebar band berkisar B= 1
kHz, dan jika
ms maka B = 500 Hz.
Tekanan dan Perpindahan
Perubahan tekanan gelombang menyebabkan molekul air mengalami
getaran.
Amplitudo pergerakan molekuler disebut pemindahan partikel, dan
tingkat perpindahannya disebut kecepatan partikel (Gambar 2.1).
Pada gelombang datar, kecepatan partikel dan tekanan bunyi dalam
satu fase, maksudnya bahwa nilai maksimum berimpit antara waktu
dan ruang.
Pulsa dan Kesaran (Jarak)
Pulsa sonar mentransmisikan sebuah letupan
(gelombang) pendek dari bunyi yang disebut pulsa
atau ping, berisikan beberapa putaran frekwensi
tertentu dari sonar.
Gambar 2.13 memperlihatkan sebuah pulsa dari 19
putaran (gelombang) yang dibangkitkan oleh sebuah
sonar dengan frekwensi pancaran 38 kHz.
Durasi pulsa (waktu dari mulai hingga akhir) adalah:
 = 19/38 = 0,5 ms
Jika kecepatan bunyi 1500 m/s, panjang pulsa dalam
Gema diterima pada waktu T setelah transmisi.
Jarak R antara target dan transduser diestimasikan dari pengukuran T.
Dua jalan (pancaran dan pantulan) sepanjang 2 R, sehingga:
T = 2R/c
R = cT/2
Apabila ada 2 target pada range R1 dan R2.Dalam rangka menyelesaikan
target dan mengukur secara individu, perbedaan rentang (R2-R1) harus
cukup besar supaya dua gema tidak tumpang tindih.
Gema dari target yang lebih dekat, dimana terdeteksi pertama, pada saat
T1 = 2R1/c, dan berlanjut selama getaran, yaitu sampai waktu (T1 + ).
Gema kedua menghasilkan sinyal yang dimulai pada T2=2R2/c. Untuk
menyelesaikan target tersebut , kita harus memiliki T2> (T1 + ) atau
R2-R1> c/2
Target Strength
Dunia perikanan paling banyak menggunakan
satu tranduser yang mempunyai fungsi ganda
yaitu yang bisa mengirimkan pulsa bunyi dan
menerima gema dari target.
Dalam kasus di atas hanya gelombang bunyi
yang dihamburkan balik ke tranduser yang punya
peran penting.
Target strength adalah ukuran logaritmik dari
proporsi energi yang ditransmisikan dengan
energi yang dihamburkan oleh target.
Untuk memahami target strength perlu memahami
beberapa parameter, yaitu:
σ : adalah ukuran unit area dalam m²
Ii
:
Intensitas
gelombang
bunyi
yang
ditransmisikan pada target
Ib : Intensitas pulsa hamburan balik
R : Jarak antara tranduser dan target
2.21
Intensitas adalah kekuatan yang ditransmisikan per
unit area, sehingga σIi adalah kekuatan gelombang
bunyi yang ditransmisikan melalui area dengan
ukuran σ.
Area permukaan dari bola dengan radius R
adalah 4ЛR², dan jika intensitas hamburan adalah
sama pada semua arah, kekuatan hamburan total
adalah:
4ЛR²Ib
σ adalah lebih digambarkan sebagai total bidang
perpotongan, untuk membedakannya dengan
quantitas yang lain, sehingga ia disebut
hamburan dari bidang perpotongan (σb).
2.2
2
Oleh karena itu Ib / σb = 4Л, nilai σ
didefinisikan dalam persamaan 2.21.
Persamaan 2.21 berlaku hanya untuk kasus
transmisi bunyi yang terus-menerus pada
amplitudo yang konstan dan tidak terjadi absorpsi,
disamping itu juga diasumsikan bahwa target
terisolasi, tidak ada target lain atau batas refleksi
cukup tertutup sehingga tidak ada gangguan.
Target strength dalam desibel diformulasikan:
TS = 10 log(σ/4Л)
Ketika formulasi di atas digunakan, nilai substitusi
untuk σ harus dalam bentuk m².
TS dan σ adalah cara alternatif yang sederhana
untuk mendiskripsikan sifat fisik yang sama dari
target, yang dinamakan kekuatan (strength)
hamburan balik.