MATERI

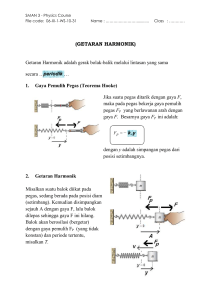
MATERI
GERAK HARMONIK SEDERHANA
Gerak harmonic sederhana adalah gerak bolak-balik benda melalui suatu titik
kesetimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan.
Gerak harmonic dapat dinyatakan dengan grafik posisi partikel sebagai fungsi waktu berupa
sinus atau kosinus. Contoh gerak harmonic antara lain adalah gerakan benda yang tergantung
pada sebuah pegas, dan gerakan sebuah bandul.
Untuk memahami getaran harmonik, kita dapat mengamati gerakan sebuah benda yang
diletakkan pada lantai licin dan diikatkan pada sebuah pegas (Gambar1).
Gambar1. Gerak benda pada lantai licin dan terikat pada pegas untuk posisi normal (a),
teregang (b), dan tertekan (c)
Anggap mula-mula benda berada pada posisi X = 0 sehingga pegas tidak tertekan atau
teregang. Posisi seperti ini dinamakan posisi keseimbangan. Jika benda ditarik kekanan
kemudian dilepaskan, maka pegasakan menarik benda kembali kearah posisi keseimbangan
(X=+). Sebaliknya, ketika benda ditekan kekiri (X = –) kemudian dilepaskan, maka pegas
akan mendorong benda kekanan, menuju posisi keseimbangan.
Gaya yang dilakukan pegas untuk mengembalikan benda pada posisi keseimbangan
disebut gaya pemulih. Besarnya gaya pemulih menurut Robert Hooke dirumuskan sebagai
berikut.
Fp=-kX
Tanda minus menunjukkan bahwa gaya pemulih selalu pada arah yang berlawanan dengan
simpangannya. Jika digabungkan persamaan diatas dengan hokum II Newton, maka diperoleh
persamaan berikut.
( )
Terlihat bahwa percepatan berbanding lurus dan arahnya berlawanan dengan simpangan. Hal
ini merupakan karakteristik umum getaran harmonik.
Syarat suatu gerak dikatakan getaran harmonik, antara lain:
1. Gerakannya periodic (bolak-balik).
2. Gerakannya selalu melewati posisi keseimbangan.
3. Percepatan atau gaya yang bekerja pada benda sebanding dengan posisi/simpangan
benda.
4. Arah percepatan atau gaya yang bekerja pada benda selalu mengarah keposisi
keseimbangan.
JENIS GERAK HARMONIK SEDERHANA
Gerak Harmonik Sederhana dapat dibedakan menjadi 2 jenis, yaitu :

Gerak Harmonik Sederhana Linier, pergerakannya ada pada satu garis lurus vertical
maupun horizintal. Misalnya penghisap dalam silinder gas, gerakosilasi air raksa / air
dalam pipa U, gerak horizontal / vertical dari pegas (pegas pada mobil), dan sebagainya.

Gerak Harmonik Sederhana Angular, pergerakannya mengayun membentuk pola
setengah lingkaran atau punbisa saja perputaran. Misalnya gerak bandul/ bandul fisis
(bandul jam), osilasiayunan torsi, dansebagainya.
1. Periode dan Frekuensi Getaran Harmonik
a. Periode dan Frekuensi Sistem Pegas
Pada dasarnya, gerak harmonic merupakan gerak melingkar beraturan pada salah satu
sumbu utama. Oleh karena itu, periode dan frekuensi pada pegas dapat dihitung dengan
menyamakan antara gaya pemulih (F=-kX) dan gaya sentry petal (F=-4π2mf2X).
2 2
-4π mf X=-kX
2 2
4π mf =k
Jadi frekuensinya adalah : Dan periodenya adalah:
Periode adalah Waktu yang digunakan dalam satu kali putaran, disimbolkan dengan T
dan satuannya (sekon).
√
Frekuensi adalah banyaknya putaran tiap satu satuan waktu, disimbolkan dengan f dan
satuannya Hz (Hertz).
√
Keterangan :
f
:frekuensi (
)
T
:periode ( s )
k
:konstanta pegas ( N/m )
m
: massa beban ( kg )
Contoh soal:
Jika massa beban yang digantung pada ujung bawah pegas 1kg, maka periode getarannya 3
sekon. Jika massa beban dilipatkan menjadi 4 kg, maka tentukan periode getarannya !
Penyelesaian:
Diketahui:
m1=1kg
T1=3s
m2=4kg
Ditanyakan: T2=...?
Jawab :
Hubungan periode pegas T, massa beban m dinyatakan dengan rumus :
√
√
√
√