ANALISA TEGANGAN

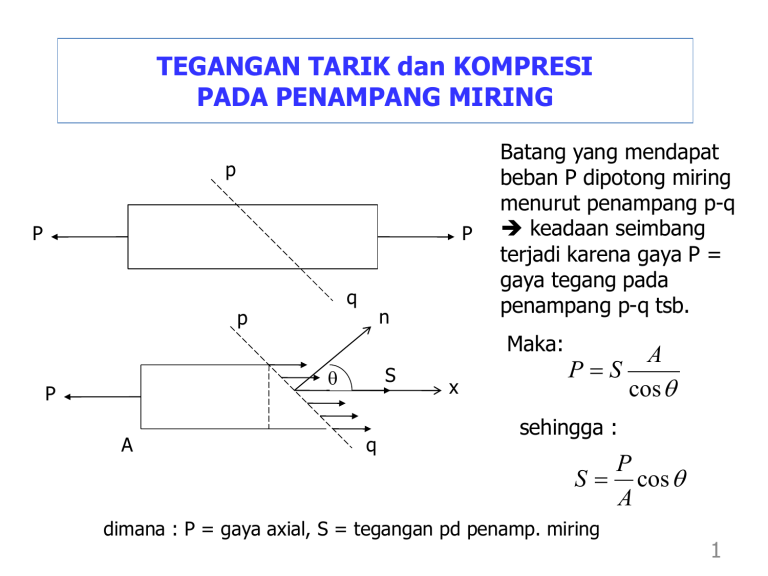
TEGANGAN TARIK dan KOMPRESI
PADA PENAMPANG MIRING
p
P
P
q
p
n
Batang yang mendapat
beban P dipotong miring
menurut penampang p-q
 keadaan seimbang
terjadi karena gaya P =
gaya tegang pada
penampang p-q tsb.
Maka:
S
q
P
A
q
x
A
PS
cos q
sehingga :
P
S  cos q
A
dimana : P = gaya axial, S = tegangan pd penamp. miring
1
Bila sx adalah tegangan batang (dipotong normal terhadap
sumbu x), maka :
sx
P
dan S  s x cosq
A
Dari persamaan diatas tampak bahwa : semakin besar sudut q
harga S semakin kecil, dan S = 0 untuk q = /2, serta S =
untuk q = 0
sx
Tegangan S pada penamp. p-q mempunyai komponen kearah
normal dan kearah tangensial :
 Komponen kearah normal  tegangan normal (sn),
 Komponen kearah tangensial  tegangan geser (t)
2
2

S
cos
q

cos
sx q
Tegangan normal : s n
Tegangan geser :
t
1
 S sin q  s x cosq sin q  s x sin 2q
2
p
sn
q
P
n
q
S
q
t
x
q
3
Tegangan normal maksimum terjadi pd harga q = 0,
yaitu :
s n(maks)  s x
Tegangan geser maksimum terjadi pd harga q = 45o,
yaitu :
1
t maks  2s x
4
Bila diperhatikan penampang p-q dan p1-q1 dan batang ditarik
dengan gaya P, maka tegangan pada elemen batang adalah seperti
pada gambar.
p1
p
q
P
q1
P
q
sn
t
sn
(+)
t
(+)
Tegangan normal yg terjadi sn diberi tanda positif, tegangan
geser t pada penamp. p-q dan p1–q1 menimbulkan kopel searah
putaran jarum jam dibefri tanda positif.
5
ANALISA TEGANGAN
KONDISI 2 DIMENSI dan 3 DIMENSI
Transformasi Tegangan 2 Dimensi
• Bila diasumsikan tegangan-tegangan sx, sy dan txy
diketahui, maka dapat dihitung kondisi tegangan
pada bidang miring dengan sudut q terhadap sumbu
x seperti pada gambar dibawah .
• Untuk sembarang sudut q  didapat harga
s dan t
6
Tegangan 2 Arah pada Bidang Miring
y
sx
txy
tyx
y
sy
s
q
tyx
sy
txy
sx
x
t
q
dx
dy
tyx
sx
x
txy
sy
7
• Tegangan normal s dan tegangan geser t pada
bidang miring tersebut dapat dihitung dengan
persamaan :
σxσy σxσy
σ

sin2θ 
2
τ
σxσ y
2
2
τxy cos2θ
τ
sin2θ  xy cos2θ
8
• Untuk suatu harga q tertentu  diperoleh harga s
maksimum dan minimum  t = 0
s maks 
s x s
s min 
2
s x s
2
2
y   s x  s

2

2
y   

t xy 




y   s x  s

2

2
y   

t xy 




2
9
Tegangan maksimum dan minimum pada bidang
miring tersebut  tegangan utama (principal
stress)
sxx  syy
 sxx  syy 
  t2xy
s1,2 
 
2
2


2
Dimana :
s1 = tegangan utama maksimum
s2 = tegangan utama minimum
10
Arah Tegangan Utama (Directions of Principal Stress) :
tan 2q p 
s



 t xy
x  s y 
2


s2
Tegangan Utama (s1)
qp
s1
qp
Tegangan Utama (s2)
11
Pada sudut q tertentu akan diperoleh tegangan geser
maksimum :
2
 s xx  s yy 
2
  t xy
t maks,min   

2


Atau dapat dihitung dengan rumus :
tmaks
s1  s2

2
12
Arah tegangan geser maksimum pada bidang miring :
tan 2q s
s x s


2

t xy
y 


½(sx +
½(sx +
½(sx +
sy)
s y)
s y)
qs
qs
½(sx +
s y)
13
Menghitung Tegangan Utama 2 Dimensi (Biaxial
Stress) dgn Lingkaran MOHR
syy
tyx
sx
x
txy
s2
txy
sxx
txy
syy
s1
tmax t
xy
s1
s1
t
Sumbu utama II
Sumbu utama I
s2
θ
2θ
s
syy
s2
sxx
Lingkaran MOHR
14
Langkah – Langkah Dasar Analisa Tegangan
untuk menentukan TEGANGAN UTAMA :
 Menggambarkan seluruh gaya yang bekerja pada benda
kerja  Diagram Benda Bebas (Hk. Statika Newton)
 Meninjau keadaan tegangan pada suatu elemen kecil di
daerah tertentu pada benda kerja  daerah deformasi
(khusus untuk pembentukan logam  deformasi plastis)
 Kondisi tegangan pada elemen secara umum :
sxx, syy, szz, txy,tyz, tzx tyx,tzy, txz ,
dimana :
txy
=
tyx, tyz
=
tzy, tzx = txz
15
Tegangan pada Sebuah Titik (Multiaxial Stress)
syy
y
y
tyz
sxx
x
z
tyx
tzy t
zx
szz
z
szz
z
txy
txz
sxx
x
x
syy
y
16
Tegangan yang bekerja pada sebuah titik dalam
kondisi 3 dimensi dapat ditulis dalam bentuk matrik
sbb :
s ij
s11 s12 s13 


 s 21 s 22 s 23


s 31 s 32 s 33 
s = tegangan
i,j = 1,2,3
17
Bila angka indeks (1,2,3) pada i,j diganti dengan arah
s dengan angka indeks yang sama
menjadi tegangan normal s, sedangkan angka indeks
yang tidak sama menjadi tegangan geser t :
sumbu (x,y,z) 
s xx

sij   t yx
 tzx
t xy
s yy
tzy
t xz 

t yz 
s zz 
18
 Menghitung ketiga tegangan utama :
 Kondisi tegangan 2 dimensi  Lingkaran Mohr
 Kondisi tegangan 3 dimensi  Lingkaran Mohr
tidak bisa dipakai, kecuali kedua tegangan geser
yang lain = 0
19
Menghitung Tegangan Utama 3 Dimensi
(Multiaxial Stress)
z
syy
szz
tzx
tzx sxx
tyz
tyx
txy
sxx
z
syy
K
sxx
txz
y
tyx txy
sYY
txz
x
szz
s
tyz
O
tzy
L
y
tzx
J
x
szz
20
z
Bidang miring KJL  Bidang Utama (Luas KJL = A)
z
K
sxx
s
tyx txy
sYY
tyz
s
txz
O
tzy
g
L
y
tzx
a
b
O
szz
n
Sy
l
Sx
J
x
Sz
m
x
Arah tegangan s  cosinus arah l, m dan n (sudut antara s dengan
sumbu x, y, z)  l = cos a, m = cos b, n = cos g
Komponen s dalam masing-masing sumbu  Sx, Sy, Sz
21
y
Karena seimbang  jumlah gaya dalam masingmasing sumbu = 0
Komponen
Luas
s
: Sx = s.l
Sy = s.m
: KOL = A.l
JOK = A.m
Sz = s. n
JOL = A.n
Jumlah gaya dalam arah sumbu x :
s.A.l – sxx.A.l – tyx. A.m – tzx.A.n = 0
(s – sxx) l – tyx.m –tzx.n = 0
22
Arah sumbu x : (s – sxx). l – tyx.m –tzx.n = 0
Arah sumbu y : – tyx.l + (s – syy). m –tzy.n = 0
Arah sumbu z : – txz.l –tyz.m + (s – szz). n = 0
Ketiga persamaan diatas adalah persamaan linear
homogen dalam l, m, n , penyelesaian pers. tsb 
dengan membuat determinannya = 0
23
Membuat determinannya = 0
s - sxx
- tyx
- tzx
- txy
s - syy
- tzy
- txz
- tyz
s - szz
=0
24
Solusinya  persamaan pangkat 3 dalam Tegangan
Utama (s):
s3 – (sxx + syy + szz) s2 + (sxxsyy + syyszz+ sxxszz – txy2
–
tyz2 –txz2) s - (sxxsyyszz + 2 txytyztxz – sxxtyz2 –
syytxz2- szztxy2) = 0
25
Persamaan Tegangan Utama tsb diatas dapat ditulis
sbb :
s3 – I1 s2 + I2s – I3 = 0
dimana koefisien invarian I1,2,3 adalah :
I1 = (sxx + syy + szz)
I2 = (sxxsyy + syyszz+ sxxszz – txy2 – tyz2–txz2)
I3 = (sxxsyyszz + 2 txytyztxz – sxxtyz2 – syytxz2-szztxy2)
26
Akar pers pangkat 3 dalam fungsi teg utama dapat diperoleh
dengan cara trial and error, atau dapat menggunakan rumus
seperti dibawah ini :
27
Dimana :



3

2 I 1  9 I 1 I 2  27 I 3 
1

 arccos
3
 23 


2
 I1



I
2




28
Arah tegangan utama dalam bentuk cosinus (l,n,m) :
s xx s  t
l 
t xy n  s s
l
1n
t zx  0
t zy  0
m
yx n 
m

yy  1 n 
2
2
2
l  m  n 1
29
Tegangan Utama (dalam kondisi 3 dimensi)
sy
y
tyz
sx
z
sz
s2
tyx
tzy tzx
sz
s3
s1
txy
txz
sx
x
s1
sy
s3
s2
s1, s2, s3 = tegangan utama
30
CONTOH SOAL (1) :
Sebuah batang lurus mempunyai penampang uniform
A mendapat beban gaya tarik axial P.
Tentukan :
a) Tegangan normal dan tegangan geser yang
bekerja pada suatu bidang miring dengan sudut q
terhadap sumbu batang (ccw).
b) Besar dan arah tegangan gesar maksimum pada
batang tersebut.
31
Penyelesaian :
Tegangan normal terhadap sumbu batang sx = P/A,
luas penampang miring dengan sudut q terhadap
sumbu batang = A/sinq  kondisi keseimbangan
gaya pada arah sumbu batang :
σ' (A/sinθ)  P atau σ'  (P sinq )/A
m
A
sx
P
s'
n
q
q
P
32
t = s’ cos q
dan
s
s'
t
Untuk
s = s’ sin q
q
P
q
sx = P/A , maka :
t = sx sinq cosq
dan
s = sx sin2q
33
Dari trigonometri :
sin 2q = 2sinqcosq dan
Maka harga
t
dan s dapat ditulis menjadi :
t  12 s x sin 2q
Harga
t
sin2q = (1- cos 2q)/2
dan
akan maksimum bila q = 45o,
s  12 s x (1  cos 2q )
s akan maksimum bila q = 90o
34
CONTOH SOAL (2)
Luas penampang sebuah batang adalah 850 mm2
mendapat beban gaya tarik axial sebesar 60 kN pada
kedua ujungnya.
Tentukan : tegangan normal dan tegangan geser
pada bidang miring dengan sudut q = 30o terhadap
arah beban.
35
Penyelesaian :
Diketahui : luas penampang batang A = 850 mm2,
beban gaya axial P = 60 kN
Ditanyakan : tegangan normal dan tegangan geser
pada bidang miring dengan sudut q = 30o terhadap
arah sumbu beban
Penyelesaian :
3
P 60 x10
s x  A  850  70,6MPa
36
t

1
2
s x sin 2q
s
t
dan
s

1
2
s x (1  cos 2q )
1
70,61  cos60o   17,65MPa
2


1


o
 70,6 sin 60   30,6MPa
2


s = 17,65 MPa
t  30,6 MPa
q = 30o
P=60 kN
37
CONTOH SOAL (3)
Luas penampang sebuah batang adalah 850 mm2
mendapat beban gaya tarik axial sebesar 60 kN pada
kedua ujungnya.
Tentukan : tegangan geser maksimumnya
38
CONTOH SOAL (4) :
Sebuah batang lurus mempunyai penampang uniform A
mendapat beban gaya tarik axial P.
Tentukan :
a) Tegangan normal dan tegangan geser yang bekerja pada
suatu bidang miring dengan sudut q terhadap sumbu
batang (ccw).
b) Besar dan arah tegangan geser maksimum pada batang
tersebut.
Jelaskan pada soal diatas dengan menggunakan penyelesaian
secara grafis
39
CONTOH SOAL (5) :
Sebuah elemen kecil pada suatu komponen mendapat
beban multiaxial sebagai berikut :
s ij
 2 7  3


 7 10 5 ksi


 3 5  5
Ditanyakan :
a) Gambar kondisi tegangan multiaxial pada elemen
kubus tersebut
b) Cos arah (l,m,n) dari tegangan utama
40
Penyelesaian :
Tegangan normal dan tegangan geser pd penampang miring pq
dari suatu batang tarik :
s n  s x cos 2 q dan t  12 s x sin 2q
Harga2 sn dan t dapat dicari secara grafis bila besarnya sx dan
q diketahui, dengan cara berikut :
41
Penyelesaian :
syy = 10 ksi
y
tyz
sxx = 2ksi
tyx
tzy tzx
szz = -5 ksi
z
szz = -5 ksi
txy = 7 ksi
sxx= 2ksi
txz
x
s1
syy = 10 ksi
42
sxx = 2 ksi , syy = 10 ksi, szz = -5 ksi,
txy = 7 ksi, tyz = 5 ksi, tzx = -3 ksi
dimana koefisien invarian I1,2,3 adalah :
I1 = (sxx
+ syy + szz) = 3 ksi
I2 = (sxxsyy + syyszz+ sxxszz – txy2 – tyz2–txz2)
= - 143 (ksi)2
I3 = (sxxsyyszz + 2 txytyztxz – sxxtyz2 – syytxz2- szztxy2)
= 95 (ksi)3
Sehingga :
43
Arah tegangan utama :
44
n = 0.183
45