efficient frontier

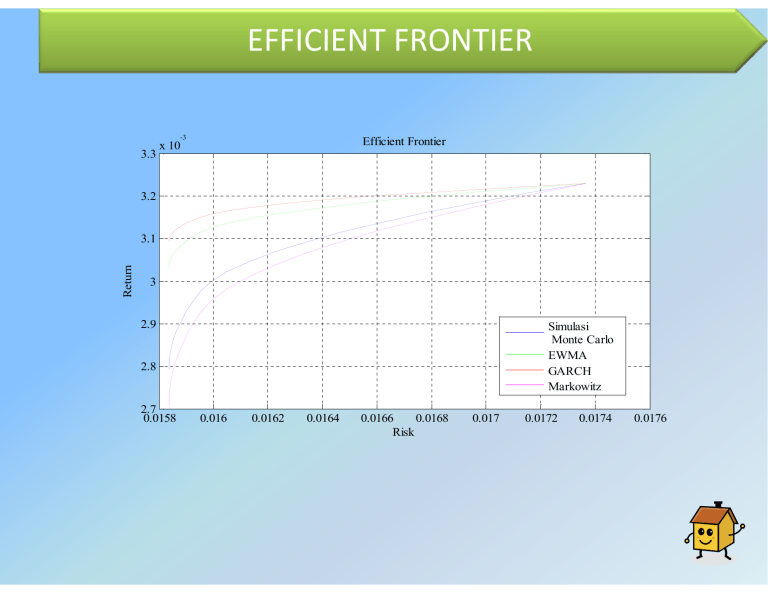
EFFICIENT FRONTIER
-3
3.3
Efficient Frontier
x 10
3.2
Return
3.1
3
2.9
Simulasi
Monte Carlo
EWMA
GARCH
Markowitz
2.8
2.7
0.0158
0.016
0.0162
0.0164
0.0166
0.0168
Risk
0.017
0.0172
0.0174
0.0176
1. Dalam pembentukan model data finansial dengan metode Exponentially
Weighted Moving Average (EWMA) saham yang digunakan tidak harus
memiliki kriteria tertentu, sehingga hampir semua saham dapat dengan
baik dimodelkan oleh metode ini. Selanjutnya, variansi saham dapat
dihitung menggunakan persamaan
VARIANSI
Saham
Variansi
Bakrie Telecom
Perusahaan Gas
Negara
Timah
Truba Alam Manunggal
Eng.
0.00103
Deviasi
Standar
0.03215
0.00023
0.01530
0.00060
0.02450
0.00169
0.04109
2. Dalam pembentukan model data finansial dengan metode Generalised
Autoregressive Conditional Heteroscedasticity (GARCH) data yang digunakan
harus berkorelasi dan memiliki efek ARCH. Setelah memastikan hal itu, maka
dilakukan estimasi parameter, dilakukan pengujian terhadap beberapa model
GARCH yang dihasilkan, dan menentukan salah satu model yang memiliki
persamaan umum sebagai berikut :
BTEL
PGAS
TINS
TRUB
Saham
VARIANSI
Variansi
Deviasi Standart
Bakrie Telecom
0.00194
0.04403
Perusahaan Gas Negara
0.00030
0.01737
Timah
Truba Alam Manunggal
Eng.
0.00097
0.00136
0.03122
0.03687
3. Dalam pembentukan model data finansial dengan Simulasi Monte
Carlo, data saham yang digunakan adalah bebas. Pembangkitan
bilangan random dilakukan dengan memasukkan harapan keuntungan
dan kovarians data historis saham. Setelah bilangan random
dibangkitkan, maka akan didapatkan harapan keuntungan dan
kovarians baru yang akan digunakan dalam membentuk portofolio.
Variansi yang dihasilkan dari hasil simulasi tersebut adalah :
Saham
Bakrie Telecom
VARIANSI
Perusahaan Gas Negara
Timah
Truba Alam Manunggal Eng.
Variansi
Deviasi Standar
0.002659
0.051566
0.001318
0.036308
0.00192
0.043817
0.002739
0.052339
4. Serangkaian portofolio yang dibentuk menjadi suatu kurva efficient frontier
merupakan portofolio yang effisien. Investor tinggal memilih portofolio yang
diinginkan dari kurva tersebut dengan mempertimbangkan preferensi risiko
dan kepercayaannya terhadap metode-metode tersebut. Investor dapat
memilih portofolio yang berada di luar kurva tersebut dengan mengetahui
bahwa portofolio tersebut tidaklah efisien. Investor juga dapat memilih
portofolio yang optimal yaitu portofolio yang berada pada batas lengkung
kurva efficient frontier karena merupakan portofolio varians minimum global
yaitu portofolio yang memberikan risiko yang paling minimum dengan return
yang sepadan.
5. Dari ketiga metode tersebut, metode yang memberikan risk
yang lebih kecil untuk return yang sama ataupun yang
memberikan return yang lebih besar untuk risk yang sama
adalah metode GARCH.
DAFTAR PUSTAKA
Ang, R. 1997. Pasar Modal Indonesia. First Edition. Indonesia : Mediasoft Indonesia. Arisona, R. 2007. Pemodelan volatilitas indeks harga saham LQ45 dengan Metode
ARCH‐GARCH. Tugas Akhir Jurusan Statistika ITS.
Badrayasa, I M. 2009. Perbandingan Sensitivitas Metode Markowitz, EWMA, dan
GARCH Terhadap Perubahan Volatilitas Dalam Pembentukan Portofolio. Tugas
Akhir Jurusan Matematika Universitas Udayana.
Brandimarte, P. 2002. Numerical methods in finance and economics : A MATLAB based introduction. Second Edition. USA : John Wiley & Son Inc.
Bollerslev, T. 1986. “Generalized Autoregressive Conditional Heteroscedasticity,”
Journal of Econometrics, 31:307–327
Box, G. E. P. , Jenkins, G. M., & Reinsel, G. C. 1994. Time Series Analysis : Forecasting and Control. Third Edition. United State of America : Prentice Hall, Inc.
Bodie, Z., Kane, A., & Marcus, A. J. 2005. Investments. Sixth Edition. Singapore : The McGraw‐Hill Companies.
Chen, N & Hong, L. J. 2007. “Monte Carlo Simulation in Financial Engineering”. Proceeding of the 2007 Winter Simulation Conference.
Endhartia, S. 2009. Analisis Portofolio Optimal pada No Short Selling dengan
Menggunakan Algoritma Markowitz. Tugas Akhir Jurusan Matematika ITS
Engle, F. R. 1982. “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation”. Econometrica, Econometric Society, 50 : 987‐1007
Fryzlewicz, P. 2007. Lecture Notes : Financial Time Series, ARCH & GARCH Models.
Department of Mathematics, University of Bristol.
Guarmat, C., & Harris, R. D. F., 2002. “Forecasting value at risk allowing for time variation in the variance and kurtosis of portfolio returns”. International Journal of Forecasting, 18: 409‐419.
Harris, R. D. F., & Yilmaz, F. 2009. “Estimation of the conditional variance–covariance matrix of returns using the intraday range”. International Journal of Forecasting, doi:10.1016.
Horasanh, M. & Fidan, N. 2007. “Portfolio Selection by Using Time Varying Covariance Matrices”. Journal of Economic and Social Research, 9:1‐22. Hull, John C. 2008. Options, Futures and Other Derivatives. Seventh Edition. India : Pearson Education India.
Husnan, S. 2003. Dasar‐dasar Teori Portofolio dan Analisis Sekuritas. Edisi Ketiga. Yogyakarta : UPP AMP YKPN. Laws, J. & Thompson, J. 2005. “Hedging effectiveness of stock index futures”. European Journal of Operational Research, 163:177–191.
Lo, M. S., 2003. “Generalized Autoregressive Conditional Heteroscedastic Time Series Models”. Partial Requirements For The Degree of Master Of Science, 1‐51.
Makridakis, S., Wheelwright, S. C., & McGee, V. E. 1999. Metode dan Aplikasi
Peramalan. Jilid Satu. Edisi Kedua. Diterjemahkan oleh Untung Sus
Andriyanto & Abdul Basith. Jakarta : Penerbit Erlangga.
McVean, J. Monte Carlo : An Alternate Approach to Efficient Frontier, Balancing portfolio risk and return with efficient frontier. <URL : http://www.slb.com/content/services/software/valuerisk/expert_paper_mo
n
te_carlo.asp>
Moskowitz, H & Serel, D. A. 2008. “Joint Economic Design of EWMA Control Charts for Mean and Variance”. European Journal of Operatinal Research, 184:157‐
168.
Podlozhnyuk, V. & Harris, M. 2008. Monte Carlo Option Pricing. NVIDIA Corporation. Santa Clara, California.
Scherer, Bernd and Martin. 2005. Introduction to Modern Portfolio Optimization with NUOPT and S‐PLUS. United State of America : Springer.
Surya, Y. & Hariadi, Y. 2004. “GARCH (2,1) Pada LQ45”. Working Papers. Bandung Fe Institute.
Widoatmodjo, S. 2006. Cara Sehat Investasi di Pasar Modal. Edisi Revisi. Jakarta : PT Elex Media Komputindo.
Winston, W. L., 1994. Operations Research Applications and Algorithms. California : Wadsworth Publishing Company
Zahrimi et al. 2009. “Modeling the Kuala Lumpur Composite Index”. European Journal of Scientific Research 25:499‐512.