Title Goes Here - Binus Repository

Matakuliah : D0696 – FISIKA II
Tahun
: 2009
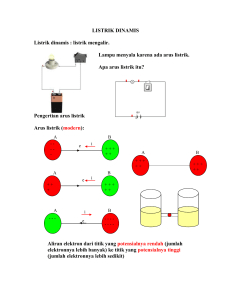
RANGKAIAN LISTRIK
Pertemuan 11-12
1. Gaya Gerak Listrik ( ggl)
Batterai dan generator listrik, yang dapat digunakan
untuk mempertahankan beda potensial antara dua titik
disebut : tempat kedudukan gaya gerak listrik ggl (ε ).
I
B
R
Sebuah batterai (ggl) dihubungkan dengan hambatan R.
Pengangkut muatan akan digerakan dalam arah I.
Bila muatan dq lewat melalui setiap penampang dalam
waktu dt, maka kerja oleh pengangkut muatan dW.
Bina Nusantara
Didefinisikan ε = dW / dq
satuan : Joule/Coulomb= volt
maka : dW = ε dq
definisi ggl (ε )
Karena ggl melakukan kerja pada pengangkut muatan,
maka energi harus dialihkan pada tempat kedudukan
ggl tersebut. Untuk :
- batterai : energi kimia dialihkan menjadi energi listrik
- generator :energi mekanis dialihkan menjadi energi listrik.
Maka pengalihan energi pada ggl merupakan proses
terbalikan ( reversible)
Batterai :
listrik
kimia
Generator(motor listrik ) : listrik
Bina Nusantara
mekanis
2. Menghitung Arus Pada Rangkaian Loop Tunggal
a
I
B
R
Sebuah rangkaian loop tunggal
Pada waktu arus i melewati hambatan R, dalam waktu dt akan
muncul energi termal sebesar : I2R dt
Pada waktu bersamaan, muatan dq bergerak melalui tempat
kedudukan ggl, hingga tempat ggl melakukan kerja :
dW = ε dq = ε I dt.
Dari prinsip kekekalan energi :
Kerja oleh ggl = energi termal atau ε I dt = I2R dt
Maka : I = ε / R
Bina Nusantara
Menetukan arus I juga dapat dilakukan dengan menggunakan
kaidah Kirchoff II, yaitu :
Jumlah aljabar perubahan potensial untuk satu lintasan penuh
dari suatu titik ke titik yang sama adalah nol.
Untuk gambar di atas, mulai dari titik a dan searah perputaran
jarum jam, maka jumlah perubahan potensial : – I R + ε = 0
atau : I = ε / R
Catatan, dalam penggunaan kaidah Kirchoff II :
- sewaktu melewati ggl searah dengan arah ggl,
perubahan potensial : + ε .
Bila ggl dilewati dalam arah berlawanan dengan ggl ,
perubahan potensialnya : - ε
- Bila hambatan R dilewati searah dengan I, perubahan
potensialnya : - I R, dan = + IR bila hambatan dilewati dalam
arah berlawanan dengan arah I.
Bina Nusantara
3. Hambatan Dalam ( r )
Setiap tempat kedudukan ggl akan mempunyai hambatan
dalam ( r ), yang merupakan bagian dari sifat alat tersebut.
b
i
r
ε
R
Hambatan dalam r tidak dapat dihilangkan, karena r dan ggl
menempati tempat yang sama pada tempat kedudukan ggl.
Dari kaidah Kirchoff II, mulai dari b dan searah perputaran
jarum jam : – I R + ε – I r = 0 atau : I = ε / ( R + r ) , maka
ggl yang baik adalah bila hambatan dalamnya r << R, hingga
arus I akan tetap sama.
Bina Nusantara
4. Beda Potensial Antara Dua Titik
b
I
o
r
ε
R
a
Menentukan beda potensial antara titik b dan a :
mulai dari titik a searah perputaran jarum jam :
Vb – I R = Va
Vb – Va =Vab = I R = {ε / ( R + r )} R
Atau : mulai dari titik a ke b melewati ggl :
Vb + I r - ε = Va
Vb – Va =Vab= ε - I r = ε – {ε / ( R + r)}r = ε { 1 – r/ ( R+r)}
Bina Nusantara
= {ε / ( R + r )} R
5. Rangkaian Multi Loop
Kaidah Kirchoff I :
Jumlah arus yang menuju suatu titik cabang = jumlah
arus yang meninggal titik cabang tersebut.
I1
I2
I3
I1 + I2 + I3 = I4 + I5
Bina Nusantara
I4
I5
ε1
ε2
a
b
R1
c
R3
Sebuah rangkaian multi loop.
Terdapat dua titik sambung,
R2
I1
I3
I2
yaitu: titik b dan titik d.
d
Terdapat 3 cabang, yaitu :
- cabang b-a-d , dengan arus I1
- cabang b-c-d , dengan arus I2
- cabang b-d , dengan arus I3
Dengan kaidah Kirchoff I dan II , akan diperoleh :
Loop kiri : mulai titik a dan searah perputaran jarum jam :
- ε1 – I3R3 + I1R1 = 0
……….. ( 1 )
Bina Nusantara
- Loop kanan: mulai titik b dan searah perputaran jarum
jam:
ε2 + I2 R2 – I3R3 = 0 ………… ( 2 )
- Titik cabang b : I2 = I1 + I3
- Titik cabang d : I1 + I3 = I2
………… ( 3 )
………… ( 4 )
Dari persamaan ( 1 ) , ( 2 ), dan ( 3 ), serta bila besar setiap
ggl dan besar setiap hambatan diketahui , maka besar arus
yang melewati masing-masing hambatan akan dapat
dihitung,
Bina Nusantara
6. Rangkaian Hambatan
Seperti kapasitor, hambatan juga dapat dirangkaikan.
(1) Rangkaian Seri Hambatan
Pada rangkaian seri, besar arus yang melewati masingmasing hambatan adalah sama.
a
R1
ε
R2
I
R3
Dari kaidah Kirchoof II, mulai dari titik a, searah perputaran
jarum jam : - I R1 - I R2 - I R3 + ε = 0
dari I = ε / R , maka
Bina Nusantara
I= ε / (R1 + R2 + R3)
Rekivalen= R1 + R2 + R3
(2) Rangkaian Paralel Hambatan
Pada rangkaian paralel, beda potensial dari masing-masing
hambatan adalah sama.
I
I1 = V / R1
I2 = V / R2
ε
R1
R2
I1
R3
I2
I3 = V / R 2
I3
i = i 1 + i2 + i3
= V / R1 + V / R2+ V / R3
= V(1 / R1 + 1 / R2+ 1 / R3)
I
dari I = V / R
Maka R ekivalen dari 3 hambatan paralel tersebut adalah :
1/ Rekivalen = 1 / R1 + 1 / R2 + 1 / R3
Bina Nusantara
7. Rangkaian RC
a
b
ε
R
S
C
Rangkaian RC di atas terdiri atas R , C dan ggl.
Mula-mula skalar S terbuka, kemudian di tutup ke a, maka
muatan/ arus I akan mengalir . Dari kaidah Kirchoff II dapat
ditunjukan bahwa ε – I R - q/C = 0
( VC = q/ C )
I = dq / dt maka : R dq/dt + q/C = ε
Solusi persamaan tersebut : q ( t ) = C ε ( 1 – e-t/(RC )
Bina Nusantara
Pada t = 0
q=0
kapasitor mulai diisi
Pada t = ∞
q=Cε
kapasitor terisi penuh
Arus yang mengalir dalam rangkaian :
I(t) = dq / dt = (ε / R) e-t/(RC)
Pada t = 0
Pada t = ∞
I=ε/R
I=0
arus maksimum
kapasitor terisi penuh
Potensial pada kapasitor :
VC(t) = q / C = C ε ( 1 – e-t/(RC)) / C = ε ( 1 – e-t/(RC)
di definisikan : τ = R.C = konstanta waktu kapasitif
yaitu : waktu yang diperlukan hingga muatan pada kapasitor
mencapai 63 % dari C ε
Bina Nusantara
8. Ammeter dan Voltmeter
a. Ammeter A : alat untuk mengukur besarnya arus listrik.
Untuk mengukur arus pada rangkaian, ammeter
disisipkan pada rangkain tersebut, hingga arus yang akan
diukur besarnya melewati ammeter .
A
I
R
ε,r
R
sebelum ammeter dipasang,
besar arus pada rangkain :
I = ε /(r + R ) :
setelah ammeter dipasang :
A
rA
Bina Nusantara
I’ = ε /(r + rA + R )
rA = hambatan dalam ammeter
Agar besar arus sebelum dan sesudah dipasang ammeter tidak
berubah, haruslah RA<< R. Ammeter yang baik bila rA kecil.
b. Voltmeter V
Alat untuk mengukur beda potensial antara dua titik.
Voltmeter dihubungkan pada kedua titik terset.
I’’
V
I
R
a I’
b
Sebelum dipasang voltmeter : Vba= I R
Setelah dipasang voltmeter : Vba = I’ R = (I – I’’) R
Agar Vba sebelum dan sesudah dipasang voltmeter tidak
berubah, haruslah : I’’ << I , atau RV >>R ,
RV= hambatan dalam voltmeter
Bina Nusantara