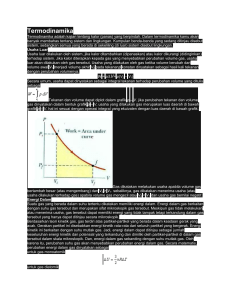
Termodinamika

D.TERMODINAMIKA
1. Kalor Jenis Gas
Suhu suatu gas dapat dinaikkan dalam
kondisi yang bermacam-macam. Volumenya
dikonstankan, tekanannya dikonstankan atau
kedua-duanya
dapat dirubah-rubah sesuai
dengan kehendak kita. Pada tiap-tiap kondisi ini
panas yang diperlukan untuk menaikkan suhu
sebesar satu satuan suhu untuk tiap satuan
massa adalah berlainan. Dengan kata lain suatu
gas mempunyai bermacam-macam kapasitas
panas. Tetapi hanya dua macam yang
mempunyai arti praktis yaitu :
- Kapasitas panas pada volume konstan
(Cv)
- Kapasitas panas pada tekanan konstan
(Cp)
Kapasitas panas gas ideal pada tekanan konstan
selalu lebih besar dari pada kapasitas panas gas
ideal pada volume konstan (Cp>Cv), dan
selisihnya sebesar konstanta gas umum
(universal) yaitu : R = 8,317 J/mol 0K.
dipanaskan (pada tekanan tetap) ; maka volume
akan bertambah dengan V.
Usaha yang dilakukan oleh gas terhadap udara
luar :
W = p. ∆ V
2. Usaha dalam (U) adalah : Usaha yang
dilakukan oleh bagian dari suatu sistem pada
bagian lain dari sitem itu pula. Pada
pemanasan gas seperti di atas, usaha dalam
adalah berupa gerakan-gerakan antara
molekul-molekul gas yang dipanaskan
menjadi lebih cepat.
Energi dalam suatu gas Ideal adalah :
U=
3
n RT
2
Cp – Cv = R
Cp = kapasitas panas jenis ( kalor jenis )
gas ideal pada tekanan konstan.
Cv = kapasitas panas jenis ( kalor jenis )
gas ideal pada volume konstan.
Berdasarkan teori kinetik gas kita dapat
menghitung panas jenis gas ideal, sebagai
berikut:
a. Untuk gas beratom tunggal ( monoatomik )
diperoleh bahwa :
5
3
γ = cP = 1,67
cP = 2 R
cV = 2 R
cV
b. Untuk gas beratom dua ( diatomik ) diperoleh
bahwa :
7
5
γ = cP = 1,4
cP = 2 R
cV = 2 R
cV
γ
= konstanta Laplace.
2. Usaha Yang Dilakukan Gas.
Temodinamika merupakan cabang ilmu
fisika yang mempelajari mengenai pengaliran
panas, perubahan-perubahan energi yang
diakibatkan dan usaha yang dilakukan oleh
panas.
1. Usaha luar (W) yaitu : Usaha yang
dilakukan oleh sistem terhadap sekelilingnya
terhadap sistem. Misalkan gas dalam ruangan
yang berpenghisap bebas tanpa gesekan
3. Kalor (Energi Panas)
Kalor dikenal sebagai bentuk energi yaitu
energi panas dengan notasi Q.
Untuk kalor pada tekanan konstan :
Qp = Cp ∆ T
Untuk kalor pada volume konstan :
Qv = Cv ∆ T
4. Hukum I Termodinamika.
Dalam suatu sistem yang mendapat panas
sebanyak ∆ Q akan terdapat perubahan energi
dalam ( ∆ U) dan melakukan usaha luar ( ∆ W )
Q (+)
Lingkungan
W (+)
sistem
∆U
Lingkungan
Q(-)
W (-)
∆Q= ∆U+ ∆W
∆ Q (+) = Kalor yang masuk sistem
∆Q
∆ Q (-) = Kalor yang keluar dari sistem
∆ U = perubahan energi dalam
∆W
∆ W (+) = Sistem melakukan usaha
pada lingkungan
∆ W (-) = Sistem dikenai usaha
Pada proses ini gas dipanaskan dengan tekanan
tetap (lihat gambar).
5.
Proses - Proses
Thermodinamika
Pada
Hukum
I
1.
Hukum I Thermodinamika untuk Proses
Isokhorik / Isovolumik (volume konstan )
sebelum dipanaskan
Pada proses ini volume sistem konstan. ( lihat
gambar )
Sebelum dipanaskan.
sesudah dipanaskan
Persamaan :
Dari ∆ Q = ∆ U + ∆ W, maka :
3
Cp ∆ T = n R ∆T + p. ∆ V
2
3
Cp ∆ T = n R ∆T + n R ∆T
2
Sesudah dipanaskan.
Cp =
Persamaan :
Dari ∆ Q = ∆ U + ∆ W, maka :
3
Cv ∆ T = n R ∆T + p. ∆ V, karena
2
isokhoris (V = konstan) ∆ V = 0 → W= 0
3
Cv ∆ T = n R ∆T
2
Cv =
Atau dengan mengingat Cv =
Sebagaimana telah dijelaskan sebelumnya
Grafik :
Dalam proses ini berlaku persamaan BoyleGayLussac
3
nR
2
V1 V2
=
T1 T2
Jika grafik ini digambarkan dalam
hubungan P dan V maka dapat grafik sebagai
berikut :
P1 P2
=
T1 T2
Jika digambarkan dalam grafik hubungan P
dan V maka grafiknya sebagai berikut :
W = luasan
Pemanasan
Pendinginan
Interpretasi :
Karena ∆ V = 0 maka dari W = p . ∆ V,
W = 0 (tidak ada usaha luar selama proses)
∆ Q = U2 - U1
Kalor yang diserap oleh sistem hanya
dipakai untuk menambah energi dalam ( ∆ U )
∆Q= ∆U
dengan
∆ U = m . cv ( T2 - T1 )
2.
3
n R , didapat :
2
Cp – Cv = R
Grafik :
Dalam proses ini berlaku Hukum Boyle-Gay
Lussac dalam bentuk :
Pemanasan
5
nR
2
Hukum I termodinamika untuk Proses
Isobarik (tekanan konstan)
W = luasan
Pendinginan
Interpretasi :
Usaha luar yang dilakukan adalah :
W = p (V2 - V1). karena itu hukum I
termodinamika dapat dinyatakan :
∆ Q = ∆ U + p ( V2 - V1 )
dw
Dari persamaan p =
→ dw = p dv
dv
w = ∫ p dv → w = luasan dibawah kurva p Vs v
Panas yang diperlukan untuk meningkatkan
suhu gas pada tekanan tetap dapat dinyatakan
dengan persamaan :
∆ Q = m cp ( T2 - T1 )
Pertambahan energi dalam gas dapat pula
dinyatakan dengan persamaan :
∆ U = m . cp ( T2 - T1 )
Karena itu pula maka usaha yang dilakukan
pada proses isobarik dapat pula dinyatakan
dengan persamaan :
∆ W = ∆ Q - ∆ U = m ( cp - cv ) ( T2 - T1
)
dengan :
m = massa gas
cp = kalor jenis gas pada tekanan tetap
cv = kalor jenis pada volume tetap.
V2
V
) = n R T2 ( ln 2 )
V1
V1
P
P
W = n R T1 ( ln 1 ) = n R T2 ( ln 1 )
P2
P2
ln x =2,303 log x
V
V
W = P1V1 (ln 2 ) = P2V2 (ln 2 )
V1
V1
P
P
W = P1V1 (ln 1 ) = P2V2 (ln 1 )
P2
P2
W = n R T1 ( ln
4. Hukum I Termodinamika untuk proses
Adiabatik
Selama proses tak ada panas yang masuk /
keluar sistem jadi Q = 0 ( lihat gambar )
3. Hukum I termodinamika untuk proses
Isothermik (suhu konstan)
Selama proses suhunya konstan (lihat gambar)
Sebelum proses
Sebelum dipanaskan.
Sesudah dipanaskan.
Persamaan :
Dari ∆ Q = ∆ U + ∆ W, karena suhunya
konstan, maka ∆ T = 0 → ∆ U = 0. Jadi berlaku ∆ Q = ∆ W
Selama/akhir proses
Persamaan :
Dari ∆ Q = ∆ U + ∆ W, Q = 0, maka
berlaku ∆ U = - ∆ W atau ∆ W = - ∆ U
Grafik :
Oleh karena tidak ada panas yang masuk /
keluar sistem maka berlaku Hukum Boyle-Gay
Lussac
PV
PV
1 1
= 2 2
T1
T2
Grafik :
Oleh karena suhunya tetap, maka berlaku
Hukum Boyle
Jika digambarkan dalam grafik hubungan P
dan V maka berupa :
P1 V2 = P2 V2
Jika digambarkan grafik hubungan P dan V
maka grafiknya berupa :
Pengembangan
Pemampatan
# Catatan : Grafik Adiabatis lebih curam
dibanding grafik isothermis
Pemanasan
Pendinginan
Interpretasi :
Karena suhunya konstan T2 = T1 maka :
∆ U = U2 - U1
= 23 n R T2 - 23 n R T1 = 0
(Usaha dalamnya nol )
Kalor yang diserap sistem hanya dipakai
untuk usaha luar saja. Dari persamaan :
V
nRT
W = ∫ p dv → W = ∫
dv → W = nRT ln 2
v
V1
Interpretasi :
Karena ∆ Q = 0 maka O = ∆ U + ∆ W
U2 -U1 = - ∆ W. Bila ∆ W negatif (-W = sistem
ditekan) usaha dalam sistem ( ∆ U ) bertambah.
Sedangkan hubungan antara suhu mutlak dan
volume gas pada proses adibatik, dapat
dinyatakan dengan persamaan PVγ = c
P1.V1γ = P2.V2γ
Dengan γ =
Cp
CV
semula. Jadi untuk melakukan usaha secara
terus menerus, suatu siklus harus melakukan
usaha secara terus menerus. Suatu siklus harus
bekerja dalam suatu siklus.
→ Konstanta Laplace
Juga berlaku persamaan :T.Vγ-1 = c
2. Efisiensi Mesin
T1.V1γ-1 = T2.V2γ-1
Usaha yang dilakukan pada proses adiabatik
adalah :
W = m . cv ( T1 - T2 )
atau
W=
Mengubah tenaga panas menjadi tenaga
mekanik pertama-tama selalu memerlukan
sebuah mesin, misalnya : mesin uap, mesin
bakar atau mesin diesel. Pengalamanpengalaman dengan mesin-mesin yang terdapat
dalam praktek membawa kita kepada hukum
Termodinamika II yang ringkasnya sebagai
berikut :
“ Adalah Tidak Mungkin Membuat Suatu
Mesin Yang Bekerja Dalam Lingkaran
Yang Tidak Menimbulkan Efek Lain
Selain Daripada Mengambil Panas Dari
Suatu Sumber Dan Merubah Panas Ini
Seluruhnya Menjadi Usaha “.
P1.V1
( V2γ-1 - V1γ-1)
1−γ
=====O0O=====
3. Siklus Carnot
6. Penerapan
Hukum
I
Siklus carnot yang disebut siklus ideal
ditunjukkan pada gambar di bawah ini.
Termodinamika .
1. Pengertian Siklus
Suatu pesawat yang dapat mengubah
seluruh kalor yang diserapnya menjadi usaha
secara terus menerus belum pernah kita jumpai.
yang ada hanya pengubahan kalor menjadi
usaha melalui satu tahap saja. Misalnya : proses
isothermis.
Agar sistem ini dapat bekerja terus-menerus
dan hasilnya ada kalor yang diubah menjadi
usaha, maka harus ditempuh cara-cara tertentu.
Perhatikan gambar di bawah ini.
- Mulai dari (P1,V1) gas mengalami proses
isothermis sampai (P2,V2 ).
- Kemudian proses isobarik mengubah sistem
dari (P2,V2) sampai (P2 , V1).
- Akhirnya proses isokhorik membuat sistem
kembali ke (P1 ,V1).
Usaha yang dilakukan sama dengan luas
bagian gambar yang diarsir proses seperti yang
ditunjukkan pada gambar diatas disebut :
SIKLUS. Pada akhir proses sistem kembali ke
keadaan semula. Ini berarti pada akhir siklus
energi dalam sistem sama dengan energi dalam
Siklus Carnot dibatasi oleh garis
lengkung isothermik dan dua garis lengkung
adiabatik. Hal ini memungkinkan seluruh panas
yang diserap (input panas) diberikan pada satu
suhu panas yang tinggi dan seluruh panas yang
dibuang (panas output) dikeluarkan pada satu
suhu rendah.
− Kurva ab dan cd masing-masing adalah
kurva pengembangan dan pemampatan
isotermis.
− Kurva bc dan da masing-masing adalah
kurva pengembangan dan pemampatan
adiabatik.
Untuk bahan perbandingan, ditunjukkan
beberapa siklus untuk berbagai jenis mesin.
4. Siklus Mesin Bakar
Siklus mesin bakar atau lebih umum disebut
siklus Otto di tunjukkan pada gambar di bawah
ini.
Siklus Otto dibatasi oleh dua garis lengkung
adiabatik dan dua garis lurus isokhorik.
Dimulai dari titik a, maka :
− Kurva ab dan cd masing-masing adalah
kurva pemampatan dan pengembangan
adiabatik.
− Garis lurus bc dan da masing-masing
adalah garis lurus untuk pemanasan
dan pendinginan isokhorik.
5.Siklus Mesin Diesel
Siklus untuk mesin diesel ditunjukkan pada
gambar di bawah ini. Siklus pada mesin diesel
dibatasi oleh dua garis lengkung adiabatik dan
satu garis lurus isobarik serta satu garis lurus
isokhorik.
-
Garis fa adalah proses pengembunan
sehingga kembali ke keadaan awalnya.
=====O0O=====
7. Hukum II Termodinamika
1. Effisiensi (daya guna mesin)
Dalam hukum II Termodinamika akan
dibahas perubahan kalor menjadi energi
mekanik melalui sebuah mesin, dan ternyata
belum ada sebuah mesin pun yang dapat
mengubah sejumlah kalor menjadi energi
mekanik seluruhnya.
Reservoir panas
Suhu mutlak T1
Q1
Dimulai dari titik a, maka :
− Kurva ab dan cd masing-masing
adalah kurva pemampatan dan
pengembangan adiabatik.
− Garis lurus bc adalah garis lurus
pemanasan isobarik.
− Garis lurus cd adalah garis lurus
pendinginan isokhorik..
6. Siklus Mesin Uap
Siklus mesin uap yang juga disebut siklus
Rankine ditunjukkan pada gambar di bawah ini.
Siklus ini dibatasi oleh dua garis lengkung
adiabatik dan dua garis lurus isokhorik, hanya
saja pada mesin uap ini terdapat proses
penguapan dan pengembunan.
W
proses
Q2
Reservoir dingin
Suhu mutlak T2
Sebuah mesin diberi energi berupa kalor Q1
pada suhu tinggi T1, sehingga mesin melakukan
usaha mekanik W. Energi yang dibuang berupa
kalor Q2 pada suhu T2.
Menurut hukum Thermodinamika I (hukum
kekekalan energi) :
Q1 = W + Q2 → W = Q1 – Q2
Effisiensi mesin adalah :
Energi yang bermanfaat
W
η=
=
Energi yang dim asukkan Q1
η=
Mula-mula air dalam keadaan cair dengan suhu
dan tekanan rendah di titik a.
- Kurva ab adalah kurva pemampatan
secara adiabatik dengan tekanan yang
sama dengan tekanan di dalam periuk
pendingin.
- Garis cd adalah proses pengubahan air
menjadi uap.
- Garis de adalah prosers pemanasan
sehingga suhu uap sangat tinggi.
- Kurva ef adalah proses pengembangan
secara adiabatik.
W Q1 − Q2
=
Q1
Q1
atau

Q 

1
η = 1 − 2  x 100%
Q

Menurut Carnot : Q ∼ T, di dapat :
Q1 T1
=
Q2 T2
sehingga effisiensi mesin carnot dapat ditulis :

T 

1
η = 1 − 2  x 100%
T

Rumus Praktis Mesin Carnot :
1. Suhu Tinggi
T1' (1 - η’) = T1(1 - η)
2. Suhu Rendah
T2' (1 - η) = T2 (1 – η’)
Sebenarnya tidak ada mesin yang
mempunyai effisiensi 100 % dan dalam praktek
effisiensi mesin kurang dari 50 %.
2. Mesin Pendingin / Refrigerator
Kalor dapat dipaksa mengalir dari benda
dingin ke benda panas dengan melakukan usaha
pada sistem. Peralatan yang bekerja dengan
cara seperti ini disebut mesin pendingin
(refrigerator), contohnya adalah lemari es
(kulkas) dan pendingin ruangan (AC).
Perhatikan gambar dibawah ini.
Reservoir panas
Suhu mutlak T1
Q1
W
pendingin
Q2
Reservoir dingin
Suhu mutlak T2
• T1 > T2
• Q 2 = kalor yang diserap dari suhu
rendah
• Q 1 = kalor yang diserap dari suhu
rendah
• W = Q 1 – Q 2 = kerja / usaha yang
diperlukan
Ukuran penampilan sebuah mesin
pendingin din yatakan sebagai koefisien
daya guna (koefisien performansi),
yang diberi lambang Kp.
Q
Q2
T2
Kp = 2 =
=
W Q1 − Q2 T1 − T2
Kulkas dan pendingin ruangan memiliki
koefisien performansi dalam jangkauan
2-6. Semakin tinggi nilai Kp, semakin
baik mesin pendingin tersebut.
3. Perumusan Kelvin-Plank Tentang
Hukum II Termodinamika
Pada dasarnya perumusan antara Kelvin
dan Plank mengenai suatu hal yang sama,
sehingga
perumusan
keduanya
dapat
digabungkan dan sering disebut : Perumusan
Kelvin-Plank
Tentang
Hukum
II
Termodinamika.
Perumusan Kelvin-Plank secara sederhana
dapat dinyatakan sebagai berikut :
“Tidak Mungkin Membuat Pesawat
Yang Kerjanya
Semata-Mata Menyerap Kalor Dari
Sebuah Reservoir
Dan Mengubahnya Menjadi Usaha”
Sebagai contoh marilah kita perhatikan
proses yang sebenarnya terjadi pada motor
bakar dan motor bensin.
− Mula-mula campuran uap bensin dan
udara dimasukkan ke dalam silinder
dengan cara menarik penghisap.
− Kemudian penghisap ditekan, dengan
demikian campuran tadi dimampatkan
sehingga temperatur dan tekanannya
naik.
− Campuran tadi kemudian dibakar
dengan loncatan bunga api listrik.
Proses pembakaran ini menghasilkan
campuran dengan temperatur dan
tekanan yang sangat tingi, sehinga
volume
campuran
tetap
(proses
isokhorik)
− Hasil pembakaran tadi mengembang,
mendorong
penghisap,
sedangkan
tekanan dan temperaturnya turun, tetapi
masih lebih tinggi dari tekanan dan
temperatur di luar.
− Katub terbuka, sehingga sebagian
campuran itu ada yang keluar sedangkan
penghisap masih tetap ditempatnya.
− Akhirnya penghisap mendorong hampir
seluruhnya campuran hasil pembakaran
itu keluar.
4. Perumusan
Clausius
Tentang
Hukum II Termodinamika
Perumusan Clausius tentang hukum II
Termodinamika secara sederhana dapat
diungkapkan sebagai berikut :
“Tidak Mungkin Membuat Pesawat
Yang Kerjanya Hanya Menyerap Dari
Reservoir Bertemperatur Rendah Dan
Memindahkan Kalor Itu Ke Reservoir
Yang Bersuhu Tinggi, Tanpa Disertai
Perubahan Lain
Sebagai contoh marilah kita lihat proses
pada lemari pendingin (lemari es) yang
bagannya pada gambar di bawah ini.
Contoh Soal dan Pembahasan :
1. Jika volume gas ideal diperbesar dua kali
volume semula dan ternyata energi
dalamnya menjadi empat kali semula,
tekanan gas tersebut menjadi ....
(A) 4 kali
(D) ¼ kali
(B) 2 kali
(E) 6,4 x 105 Pa
(C) ½ kali
Jawaban : B
V2 = 2 V1, U2 = 4 U1, maka P2 = ?
3
Dari U = n R T , padahal PV = n R T ,
2
sehingga U ∼ PV. Jadi dari U2 = 4 U1
diperoleh P2V2 = 4 P1V1. Dengan
memasukkan V2 = 2 V1, maka P2 = 2 P1
−
−
−
−
Zat cair di dalam wadahnya pada tekanan
tinggi harus melalui saluran yang sempit,
menuju ke ruang yang lapang
(Avoporator). Proses ini disebut : Proses
Joule-Kelvin.
Tiba di ruang yang lapang, temperatur
dan tekanan zat cair tadi berkurang, dan
zat cair juga menguap. Untuk menguap
maka zat cair ini memerlukan kalor yang
diserap dari reservoir T2 (suhu reservoir
dingin = suhu benda yang akan
didinginkan).
Kemudian uap pada tekanan rendah ini
masuk
ke
dalam
kompresor,
dimampatkan, sehingga tekanannya dan
temperaturnya naik. Temperatur uap ini
lebih tingi dari temperatur reservoir T1
(temperatur suhu tingi) dan T1 > T2
Di dalam kondensor uap ini memberikan
kalor pada reservoir T1. Sebagai
reservoir T1 dapat digunakan udara
dalam kamar atau air. Zat yang sering
dipakai pada pesawat pendingin adalah :
Amoniak. Pada proses ini selain
pemindahan kalor dari reservoir dingin
T2 ke reservoir T1, terjadi pula perubahan
usaha menjadi kalor yang ikut dibuang di
T1 .
=====O0O=====
2. Sebanyak 1,5 m3 gas helium yang bersuhu
27oC dipanaskan secara isobarik sampai
87oC. Jika tekanan gas helium 2 x 105 N/m2,
gas helium melakukan usaha luar sebesar ....
(A) 60 kJ
(D) 480 kJ
(B) 120 kJ
(E) 660 kJ
(C) 280 kJ
Jawaban : A
V1 = 1,5 m3, T1 = 300 K, T2 = 360 K, dan P
= 2 x 105 N/m2, maka W = ?
Ingat ! W = p ∆V → W = p (V2 – V1)
T
V V
Proses Isobarik 1 = 2 →V2 = 2 V1
T1 T2
T1
360
V2 =
(1,5) m 3 = 1,8 m 3 . Jadi :
300
W = 2 x 105 (0,3) J = 60 kJ
3. Sejumlah gas ideal dengan massa tertentu
mengalami pemampatan secara adiabatik.
Jika W adalah kerja yang dilakukan oleh
sistem (gas) dan ∆T adalah perubahan suhu
dari sistem, maka berlaku keadaan ....
(A) W = 0; ∆T > 0
(D) W < 0; ∆T > 0
(B) W = 0; ∆T < 0
(E) W < 0; ∆T < 0
(C) W > 0; ∆T = 0
Jawaban : D
Karena pemampatan, maka volume
diperkecil yang mengakibatkan W < 0.
Dari Q = W + ∆ U. Proses adiabatis Q = 0,
sehingga 0 = W + ∆ U → ∆ U = - W.
Karena W < 0, maka ∆ U > 0, sehingga :
∆T>0
4. Suatu gas yang volumenya 0,5 m3 perlahanlahan dipanaskan pada tekanan tetap
sehingga volumenya menjadi 2 m3. Jika
usaha luar gas tersebut 3 x 105 joule,
tekanan gas adalah ....
(A) 6 x 105 N m-2 (D) 2 x 105 N m-2
(B) 4 x 105 N m-2 (E) 1,5 x 105 N m-2
(C) 3 X 105 N m-2
(A) 1, 2 dan 3
(B) 1 dan 3
(C) 2 dan 4
Jawaban : D
Jawaban : B
(1) Pernyataan benar. Proses isochorik
(2) Pernyataan salah. Usaha dari A ke B
Isokhorik → W = 0
(3) Pernyataan benar. Karena Q < 0
(4) Pernyataan salah. Grafik isotermik
mestinya melengkung
Ingat ! W = p ∆V → p =
W
(V2 − V1 )
3 x 10 5
N m-2 = 2 x 105 N m-2
p=
3
2
5. P(N m-2)2
3
PB
PA
1
V (m3)
0
VA
VB
Sebuah mesin kalor kecil menjalani siklus
seperti pada gambar dengan
PA = 1,2 x 105 Pa
PB = 7,2 x 105 Pa
VA = 2,5 x 10-4 m3
VB = 2 x 10-3 m3
Jika mesin bekerja 6 siklus per sekon,
berapa daya keluaran mesin itu?
(A) 6300 W
(D) 525 W
(E) 87,5 W
(B) 3150 W
(C) 1050 W
Jawaban : B
6 siklus = 1 detik → 1 siklus =
1
det ik
6
W = luasan segitiga kurva p-V
W = ½ (PB − PA ) (VB − V A )
W = ½ (6 x 105) (2 – 0,25) 10-3J = 525 J
W
525
p=
→ p=
watt → p = 3150 W
1
t
6
2
6.
P (N/m ) C
B
5
2
A
V (m3)
0
1
3
Dari proses sebuah mesin dengan gas ideal
yang digambarkan dalam diagram di
samping, maka pernyataan yang benar ialah
....
(1). proses dari A ke B adalah proses
isokhorik
(2). usaha yang dilakukan dalam proses
dari A ke B adalah 6 joule
(3). pada proses dari B ke C kalor keluar
(4). proses dari C ke A adalah proses
isotermal
Pernyataan diatas yang sesuai adalah :
(D) 4
(E) semua salah
7. Sejumlah gas pada suhu 7oC dan tekanan
1,0 x 105 N/m2 dimampatkan secara
isotermal sehingga volumenya menjadi
sepertiga volume semula. Gas itu kemudian
mengembang
secara
adiabatik
ke
volumenya semula. Jika γ = 1,40, hitung
tekanan akhir gas.
(A) 3,2 x 104 Pa
(D) 3,1 x 105 Pa
4
(B) 6,4 x 10 Pa
(E) 6,4 x 105 Pa
(C) 8 x 104 Pa
Jawaban : B
TA = (7 + 273) K = 280 K
PA = 1,0 x 105 N/m2
VB = ⅓ VA. dan γ = 1,40
PC = ?
Soal diatas dapat diilustrasikan sebagai
berikut :
P
PB
B
PA
A
PC
C
V
VB
VA = VC
Proses A-B (Proses Isotermik):
V
PA V A = PB VB → PB = A PA
VB
5
2
PB = 3 (1,0 x 10 N/m ) = 3 x 105 N/m2
Proses B-C (Proses Adiabatik):
γ
V 
PB.VBγ = PC.VCγ → PC =  B  PB
 VC 
1, 4
 1 VA 
PC =  3  (3 x 105 N/m2)
 VA 


Pc = 6,4 x 104 Pa
8. Siklus Carnot dibatasi oleh dua proses
yaitu….
(A) Isobarik dan isotermik
(B) Isobarik dan isokhorik
(C) Isotermik dan adiabatik
(D) Isotermik dan isokhorik
(E) Isokhorik dan isentropik
2.
P
A
B
5
2
Jawaban : C
Cukup jelas ! Lihat kembali teori dasarnya
10. Sebuah mesin Carnot yang menggunakan
reservoir suhu tinggi 800 K mempunyai
efisiensi 20%. Untuk menaikkan efisiensi
menjadi 36%, maka suhu reservoir suhu
tinggi dinaikkan menjadi…..
(A) 928 K
(D) 1200 K
(B) 1000 K
(E) 1380 K
(C) 1160 K
Jawaban : B
Gunakan rumus praktis :
T1' (1 - η’) = T1(1 - η)
T1' (1 – 0,36) = 800(1 – 0,2) → T1' = 1000 K
C
V
0
9. Suatu mesin menerima 200 kalori dari
sebuah reservoir bersuhu 400 K dan
melepaskan 175 kalor ke sebuah reservoir
lain yang suhunya 320 K. Efisiensi mesin
itu adalah ....
(A) 12,5%
(D) 25,0%
(B) 14,3%
(E) 87,5%
(C) 20,0%
Jawaban : A
 Q 
η = 1 − 2  x 100 %
 Q1 
 175 
η = 1 −
 x100% = 12,5 %
 200 
D
2
4
Sejumlah gas ideal menjalani siklus
ABCDA (lihat gambar). Suhu di titik C =
400 K, maka ....
1. kalor yang diserap gas per siklus 20 J
2. usaha gas 6 J
3. perubahan energi dalam gas 2 J
4. suhu di titik A 500 K
Pernyataan diatas yang sesuai adalah :
(A) 1, 2 dan 3
(D) 4
(B) 1 dan 3
(E) semua benar
(C) 2 dan 4
3. Perhatikan pernyataan-pernyataan berikut ..
(1). Pada proses isokhorik, gas tidak
melakukan usaha
(2). Pada proses isobarik, gas selalu
mengembang
(3). Pada proses adiabatik, gas selalu
mengembang
(4). Pada proses isotermik, energi dalam gas
tetap
Pernyataan yang sesuai dengan konsep
termodinamika adalah ....
(A) (1) dan (2)
(B) (1), (2), dan (3)
(C) (1) dan (4)
(D) (2), (3), dan (4)
(E) (3) dan (4)
4.
P (N/m2)
B
=====O0O=====
1
Soal-soal :
1.
P (N/m2)
25
20
15
A
B
V (m3)
0
8 16
A
1
C
VB
Jika perubahan energi dalam gas pada
proses C sama dengan perubahan energi
dalam pada proses AB, besar usaha yang
dilakukan gas pada proses AB = ....
(A) 420 joule
(D) 240 joule
(B) 300 joule
(E) 210 joule
(C) 280 joule
C
3
2
V (m3)
Gas menjalani proses ABC. Kalor yang
dibutuhkan untuk proses tersebut adalah ....
(A) 3 joule
(D) 10,5 joule
(B) 4,5 joule
(E) 12 joule
(C) 7,5 joule
5. Suatu sistem mengalami proses adiabatik.
Pada sistem dilakukan usaha 100 J. Jika
perubahan energi dalam sistem adalah ∆U
dan kalor yang diserap sistem adalah Q,
maka ....
(A) ∆U = - 1000 J
(D) Q = 10 J
(B) ∆U = 100 J
(E) ∆U +Q = -100 J
(C) ∆U = 0
6.
P
(C) 2 dan 4
B
PB
10.
PA
A
C
a
Q1
b
T1 = 900 K
V
0
VA
VB
Sebanyak 10 mol gas ideal monoatomik
menjalani siklus BCA (AB lurus) seperti
pada gambar.
PA = 2/3P B = 8,3 X 105 n m-2
VA = 1/2 VB TA = 103 K
R = 8,3 J mol -1 K-1
Jumlah kalor yang diserap gas selama
proses AB adalah ....
(A) 5,2 x 105 J
(D) 2,1 x 105 J
5
(B) 4,7 x 10 J
(E) 1,2 x 105 J
(C) 3,6 x 105J
7. Sejumlah gas ideal bermassa m menjalani
proses pada tekanan tetap P. Jika
volumenya berubah dari V1 menjadi V2 dan
suhunya berubah dari T1 dan T2 sedangkan
cp adalah kalor jenis pada P tetap, dan cv
adalah kalor jenis pada V tetap, naka
perubahan energi dalamnya adalah ....
(A) mcp (T2- T1)
(B) mcp (V2- V1)
(C) mcv(T2- T1)
(D) mcv(V2- V1)
(E) mcp (V2T2- V1T1)
8. Sebuah silinder mesin diesel berisi udara
dengan volume 90 cm3 pada suhu 27oC dan
tekanan 1 atm. Udara itu dimampatkan
secara adiabatik sehingga volumenya
menjadi 15 cm3. dengan menganggap udara
mengikuti sifat gas ideal dengan γ = 1,4 dan
1 atm = 1 x 105 N/m2, tentukan besar suhu
udara jika 61,4=12.
(A) 150 K
(D) 450 K
(B) 750 K
(E) 600 K
(C) 300 K
9. Sejumlah gas ideal bermassa m menjalani
proses pada tekanan P yang tetap. Jika
volumenya berubah dari T1 menjadi T2
sedangkan cp = kalor jenis pada P konstan
dan cv = kalor jenis pada volume konstan,
maka usaha (kerja) yang dilakukan oleh gas
dinyatakan sebagai ....
(1) P(V2 – V1)
(2) m(cp – cv )(T2- T1)
(3) mcp(T2- T1)
(4) mcv (T2- T1)
Pernyataan diatas yang sesuai adalah :
(A) 1, 2 dan 3
(D) 4
(B) 1 dan 3
(E) semua benar
c
d T2 = 600 K
Q2
Pada grafik P-V mesin Carnot di samping,
W = 2 x 105 J. Banyaknya kalor yang
dilepas oleh mesin tiap siklus adalah ....
A. 3 x 105 J
D. 6 x 105 J
B. 4 x 105 J
E. 6 x 106 J
5
C. 5 x 10 J
11. Sebuah mesin Carnot yang reservoir suhu
rendahnya 27oC memiliki daya guna 405.
jika daya gunanya akan diperbesar menjadi
50%, reservoir suhu tingginya haurs
dinaikkan sebesar ....
(A) 25 K
(D) 100 K
(B) 50 K
(E) 150 K
(C) 75 K
12. Suatu mesin Carnot bekerja di antara suhu
600 K dan 300 K dan menerima masukan
kalor 1000 J. Usaha yang dilakukan mesin
adalah ....
(A) 300 J
(D) 600 J
(B) 400 J
(E) 700 J
(C) 500 J
13. Suhu dalam suatu ruangan bermesin
pendingin T2 = -23oC sedangkan suhu di
luar T1 = 27OC. Setiap 30 menit dapat
dikeluarkan kalor Q1= 3 X 106 J. Daya
listrik yang terpakai dalam menjalankan
mesin pendingin Carnot itu besarnya ....
1
5
(A)
x10 4 watt
(D)
x10 4 watt
36
18
1
(B) 10 4 watt
(E) x10 4 watt
18
1
(C) x10 4 watt
6
14. Suatu pesawat pendingin memiliki koefisien
daya guna = 6,5. Jika temperatur ruang
(reservoir) yang bersuhu tinggi ialah 27oC,
suhu ruang temperatur rendah ialah ....
(A) – 10oC
(D) – 13oC
o
(B) – 11 C
(E) – 14oC
(C) – 12oC
15. Suhu di dalam ruangan suatumesin
pendingin (kulkas) 0oC dan suhu di luar 27o
C. Setiap jam panas yang dikeluarkan dari
ruangan ialah 6,7 x 106 joule. Berapa watt
besar daya listrik yang dipakai untuk kulkas
tersebut?
(A) 92 W
(B) 6,0 x 105 W
(C) 184 W
(D) 200 W
(E) 132,48 W
16. Suatu sistem mengalami perubahan dari
keadaan 1 ke keadaan 2 melalui berbagai
lintasan proses. Besaran berikut ini yang
perubahannya tidak bergantung pada
lintasan yang ditempuh adalah ....
(1) usaha
(3) kalor
(2) entropi
(4) energi dalam
Pernyataan diatas yang sesuai adalah :
(A) 1, 2 dan 3
(D) 4
(B) 1 dan 3
(E) semua benar
(C) 2 dan 4
17. Mesin kalor Carnot mengambil 1000 kkal
dari reservoir 627oC dan mengeluarkannya
pada reservoir 27oC. Kalor yang
dikeluarkan ke reservoir 27oC adalah ....
(A) 43,1 kkal
(D) 666,7 kal
(B) 333,3 kkal
(E) 956,9 kal
(C) 600 kkal
18. Sebuah
pesawat
pendingin
Carnot
mempunyai koefisien kinerja 6,5. Jika
reservoir yang tinggi bersuhu 27˚C, maka
reservoir suhu rendahnya bersuhu….
(A) – 5˚C
(D) – 12˚C
(B) – 8˚C
(E) – 13˚C
(C) – 10˚C
19. Koefisien performansi sebuah kulkas adalah
5,0.
Besar
energi
listrik
untuk
memindahkan 3000 J. Kalor dari makanan
di dalam kulkas adalah….
(A) 600 J
(D) 12000 J
(B) 1500 J
(E) 15000 J
(C) 5000 J
20. Sebuah mesin Carnot memiliki efisiensi
40% menghasilkan daya keluaran 100 MW
dan membuang kalor pada reservoir
bersuhu 27˚C. Kalor tiap sekon yang
dibuang ke suhu rendah sebesar….
(A) 50 MJ
(D) 250 MJ
(B) 100 MJ
(E) 350 MJ
(C) 150 MJ
=====O0O=====