SISTEM

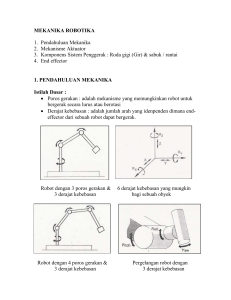
MODEL dalam SISTEM
2016
Definisi Umum
• Sistem adalah sekelompok bagian atau komponen yang bekerja
sama sebagai suatu kesatuan fungsi. (Salisbury)
• Sistem adalah suatu kesatuan yang terdiri dari sejumlah bagianbagian, atribut dari bagian dan hubungan antara bagian dengan
atribut. (Pilecki)
• Sistem adalah prosedur yang terorganisir dan mapan yang
membuahkan hasil. (Robert Allen & Mark Victor Hansen).
• Sistem adalah sekumpulan komponen yang saling berinteraksi dan
bekerja sama untuk mencapai tujuan yang sama. (Bertalanffy)
• Sistem adalah himpunan dari unsur-unsur yang saling berkaitan
sehingga membentuk suatu kesatuan yang utuh dan terpadu
(Ramon McLeod)
• Sistem adalah tatanan yang menggambarkan adanya rangkaian
berbagai komponen yang memiliki hubungan serta tujuan bersama
secara serasi, terkoordinasi yang bekerja atau berjalan dalam
jangka waktu tertentu dan terencana. (Umar Fahmi Achmadi)
Definisi Sistem Dalam Ranah Engineering
 Perangkat/alat/algoritma yang beroperasi
berdasarkan sinyal masukan (input), mengikuti
aturan tertentu/terdefinisi (biasanya berbentuk
persamaan matematis), dan menghasilkan sinyal
keluaran (output) atau respons sistem.
 Maka sistem terdiri atas komponen-komponen
dan/atau kombinasinya yang membentuk operasi
kerja tertentu untuk menghasilkan keluaran yang
sudah direncanakan.
masukan
keluaran
PROSES
• Masukan : bisa data dan/atau informasi
• Proses : operasi kerja tertentu yang akan
mengubah/mengolah masukan menjadi bentuk
tertentu yang sesuai dengan rencana
• Keluaran : hasil pengubahan/pengolahan masukan
Contoh :
gas
MOBIL
kecepatan
KOMPUTER
tampilan
TUBUH
kesehatan
rem
keyboard
mouse
makanan
minuman
Contoh :
• Permintaan
• Daya beli
• Bahan baku
• Produksi
• Keuntungan
• Distribusi
• Kondisi politik
• Dlsb.
PASAR
harga
Model Sistem
• Seorang insinyur dalam membangun sistem harus
membuat model terlebih dulu.
• Model adalah representasi lengkap dari sebuah sistem
namun dibuat dalam skala sederhana.
• Model dibuat untuk mensimulasikan dan memperhitungkan segala hal terkait sistem yang akan dibangun.
• Model berguna untuk :
 Melakukan analisis
 Melakukan simulasi
 Memperhitungkan risiko
Tahap Pembentukan Model
Mendefinisikan
masalah dengan rinci
+
Merumuskan masalah
secara terstruktur
MODEL
MULAI
+/KOREKSI
PENGUJIAN
STOP
Contoh
• Seorang insinyur hendak membangun sebuah oven
pemanggang roti. Maka tahap paling awal adalah
mendefinisikan masalah secara rinci, misalnya:
 Jenis roti yang akan dipanggang
 Jumlah/volume ruang panggang
 Range temperatur
 Jenis pemanas
 Sistem pengendalian
 Sistem monitor proses pemanggangan
 Dlsb.
• Masalah disusun dalam struktur yang sesuai :
 Jenis roti yang akan dibuat adalah roti kering dengan
ukuran maksimum tertentu.
 Timer dan suhu diatur dan selalu dikendalikan.
 Pengendali secara otomatis menghidup-matikan
pemanas untuk mendapatkan suhu yang optimal.
 Sistem monitor bekerja untuk memonitor suhu.
• Dibuat model awal dengan mengakomodasikan durasi
waktu dan arus listrik.
Listrik
SAKLAR dan
TIMER
PEMANAS
OVEN
Panas
• Setelah pengujian, ada masalah : suhu tidak terkendali.
• Dilakukan koreksi dengan mengendalikan suhu.
• Model awal dikoreksi : diberikan untai umpan balik dari
sensor suhu untuk memutus arus listrik dari saklar.
listrik
SAKLAR dan
TIMER
PEMANAS
OVEN
UDARA
PANAS
MEKANISME
SENSOR
PENGENDALI
PANAS
• Model akhir : semua permasalahan yang mungkin timbul
diberikan solusinya.
listrik
SAKLAR dan
TIMER
PEMANAS
OVEN
+
UDARA
PANAS
PEMANAS
TERPROGRAM
PEMANAS GANDA
(ATAS-BAWAH)
MEKANISME
SENSOR
PENGENDALI
PANAS
DISPLAY SUHU
Sistem Dasar
• Empat jenis sistem dasar :
• Tanpa umpan-balik (open-loop)
x
y
SISTEM
• Dengan umpan-balik (closed-loop)
x
+
SISTEM
UMPAN-BALIK
y
Komponen dalam Sistem Berumpanbalik
Arah maju
Gangguan
d
masukan
a
Sinyal
aktuasi
Elemen
kendali
b
g1
g
Keluaran
terkendali
c
SISTEM
Variabel
termanipulasi
f
Elemen
umpan-balik
Arah balik
g2
e
Contoh Pengaruh Perubahan
• Tanpa umpan-balik (open-loop)
SISTEM
x
y y 1000 x
Gain = 1000
Jika gain sistem berubah, maka keluaran langsung terpengaruh.
• Dengan umpan-balik (closed-loop)
x
x-(y/10)
+
SISTEM
Gain =1000
y/10
UMPAN-BALIK
Gain = 1/10
y
Contoh
Buat sistem tanpa umpan-balik dan dengan
umpan-balik dari rangkaian di samping ini.
Jawab :
Keluaran sistem (pembagi tegangan) :
Persamaan ini sudah menggambarkan sistem tanpa umpan-balik :
Untuk membuat sistem dengan umpan-balik, dihitung keluaran V2
dalam kaitannya dengan arus yang mengalir I :
Keluaran V2 ternyata mengandung V2 sehingga merupakan umpanbalik :
Contoh Aplikasi : Model Matematis Sistem Lengan Robot
Buat model open-loop (tanpa umpan-balik) dan model closed-loop
(berumpan-balik) dari sebuah lengan robot sederhana yang bisa
bergerak linier kiri-kanan (dalam sumbu-x) yang digerakkan oleh
sebuah motor. Motor memiliki gain = 2 dan plant (lengan robot)
memiliki gain =10. Perhitungkan adanya gangguan (misalnya
gesekan, massa).
Jawab :
Model sederhana open-loop :
x = tegangan untuk menggerakkan motor (elemen kendali), u =
elemen gangguan, y = keluaran gerak lengan robot.
Maka model matematisnya :
 Dari persamaan ini tampak bahwa gangguan memiliki pengaruh
yang besar, yakni 10 kali dari kondisi awal.
 Untuk mengurangi pengaruh gangguan, maka dirancang model
closed-loop.
• Adanya gangguan yang menyebabkan ketidakakuratan gerak
lengan robot bisa dideteksi dengan sensor.
• Yang perlu diperhatikan : antara keluaran dan masukan tidak
sejenis, sehingga harus ada pengubah yang sesuai.
• Contoh sistem dengan umpan-balik :
• Keluaran gerak lengan dideteksi dengan sensor k yang akan
mengubah kesalahan gerak menjadi tegangan koreksi k.y.
• Sebuah elemen aktuasi A diperlukan untuk menyesuaikan
masukan dari elemen kendali.
Maka persamaan keluarannya :
……………… (2)
Agar sistem menghasilkan keluaran yang akurat, maka Pers. (1)
harus sama dengan Pers. (2) :
 Tampak bahwa dengan closed-loop gangguan sudah sangat
diperkecil.
Bagan Kotak Sistem Kendali
• Bagan kotak : representasi hubungan sebab-akibat
suatu sistem dalam bentuk bagan.
• Kotak berisi deskripsi elemen, bati (gain), atau
simbol operasi matematik yang akan direlasikan
dengan masukan dan menghasilkan keluaran.
• Arah panah menunjukkan aliran informasi atau
aliran sinyal.
• Operasi penjumlahan dan pengurangan (disebut juga
pembanding) biasanya digambarkan secara spesifik :
menjadi lingkaran kecil (disebut titik penjumlahan
summing point) dengan tanda yang sesuai dengan arah
panah (plus atau minus) memasuki lingkaran.
• Masukan bisa berjumlah banyak, tergantung sistem.
• Keluarannya merupakan penjumlahan dari semua
masukan.
• Titik berangkat (takeoff/pickoff point) : titik yang
bisa disambungkan dengan banyak sinyal dengan nilai
yang sama.
• Fungsinya : meneruskan sinyal ke sembarang tujuan
tanpa ada perubahan nilai.
• Contoh :
Bentuk Kanonikal Sistem Kendali Berumpanbalik
G = fungsi transfer langsung = fungsi transfer maju
H = fungsi transfer umpan-balik
GH = fungsi transfer simpal (loop)
C/R = fungsi transfer simpal tertutup = nisbah kendali
E/R = nisbah sinyal pengaktuasi = nisbah kesalahan
B/R = nisbah umpan balik primer
Tipe Bagan Kotak Sistem Kendali
Transformasi Bagan Kotak
• Bagan suatu sistem yang terdiri dari banyak kotak bisa
disederhanakan menjadi satu kotak sederhana dengan fungsi
alih tunggal.
• Metode transformasinya :
a. Hubungan Seri/Cascade
b. Hubungan Paralel/Cascode
c. Simpal (Loop) Umpan-Balik
d. Penjumlah dan/atau Pembanding
 Kedua bentuk di atas hasilnya sama.
Penjumlah dan/atau Pembanding (lanjut)
 Kedua bentuk di atas hasilnya sama.
e. Pemindahan Titik Berangkat (Take off point)
Pemindahan Titik Berangkat (Take off point) (lanjut)
Representasi Rangkaian Pasif dalam Laplace
a. Komponen Pasif
Dinyatakan dalam bagan kotak :
b. Komponen Pasif Hubung Seri
Persamaan tegangannya :
Transformasi Laplace-nya :
Bagan kotaknya :
Proses Penyusunan Bagan Kotak
Tahapan :
• Turunkan persamaan dari rangkaian.
• Tentukan transformasi Laplace-nya.
• Nyatakan persamaan transformasi Laplace ke dalam
bentuk bagan kotak.
• Susun semua elemen dalam bagan kotak secara
lengkap.
Contoh
Buat bagan kotak sistem dari
rangkaian RC di samping ini.
Jawab :
• Persamaan arus dan tegangan :
ei  eo
i
R
eo
Maka bagan lengkap sistemnya :
idt


C
Contoh
Buat bagan kotak sistem dari
rangkaian RL di samping ini.
Jawab :
• Persamaan arus dan tegangan :
Maka bagan lengkap sistemnya :
Ls
Contoh
Buat bagan kotak sistem dari
rangkaian LRC di samping ini.
Jawab :
• Persamaan arus dan tegangan
dalam ranah s :
Contoh : Sederhanakan bagan kotak sistem pengendalian ini
ke bentuk kanonikal.
Langkah 1 : gabung semua kotak seri :
Langkah 2 : gabung semua kotak paralel :
Langkah 3 : hilangkan semua simpal umpan balik minor :
Langkah 4 : maka hasil akhir :
Contoh soal-soal transformasi bagan kotak : cari fungsi transfernya !
Cari fungsi transfernya !
Sederhanakan !
Grafik Aliran Sinyal
• Merupakan bentuk lain untuk menyatakan
hubungan antar komponen dalam bentuk simpal
(loop) dan lintasan.
• Simpul dengan satu jalan masuk
 x2 = ax1
• Cabang Cascade/seri :
• Cabang Cascode/paralel :
• Penyederhanaan simpul campuran :
• Penyederhanaan
• Contoh :
• Contoh :