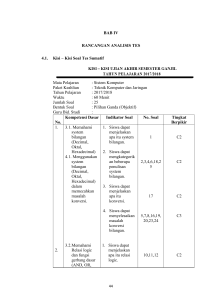
Aplikasi Teori Bilangan

APLIKASI TEORI BILANGAN
Disusun untuk memenuhi salah satu tugas Mata Kuliah Teori Bilangan
Oleh,
Dini Nur Hanifah 142151233
PROGRAM STUDI PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SILIWANGI
TASIKMALAYA
2015
2
Bagi mahasiswa Pendidikan Matematika maupun non-pendidikan mungkin sudah
tidak asing dengan salah satu mata kuliah Teori Bilangan. Teori bilangan (number
theory) adalah bagian dari matematika murni yang khusus mempelajari bilangan
bulat. Pernahkan kita bertanya untuk apa sebenarnya kita mempelajari teori
bilangan? Apa kegunaan atau aplikasi teori bilangan? Atau ada yang bertanya
apakah ilmu yang mereka pelajari ini akan berguna pada kehidupan sehari-hari
atau hanya menjadi pengetahuan semata. Kebanyakan orang dari kita mempelajari
sebuah disiplin ilmu tetapi tidak tau apa kegunaan atau aplikasi dari ilmu tersebut.
Oleh sebab itu, disini saya akan memaparkan berbagai aplikasi teori bilangan.
A. Aplikasi Teori Bilangan dalam Bidang Teknologi
1. Penerapan Teori Bilangan dalam Sistem Bilangan
Sistem bilangan atau number sistem adalah suatu cara untuk
mewakili besaran suatu item fisik. Sistem bilangan menggunakan
bilangan dasar atau basis (base/radix) tertentu.
Dalam hubungannya dengan komputer, ada 4 jenis Sistem
Bilangan yang dikenal yaitu: Desimal (Basis 10), Biner (Basis 2), Oktal
(Basis 8) dan Hexadesimal (Basis 16). Berikut penjelasan mengenai 4
sistem bilangan ini:
a. Desimal (Basis 10)
Desimal (Basis 10) adalah sistem bilangan yang paling umum
digunakan dalam kehidupan sehari-hari. Sistem bilangan desimal
menggunakan basis 10 dan menggunakan 10 macam simbol bilangan
yaitu:{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Sistem bilangan desimal dapat berupa
integer desimal (decimal integer) dan dapat juga berupa pecahan
desimal (decimal fraction).
Manfaat utama dari sistem bilangan desimal adalah bahwa
mereka lebih mudah digunakan dobandingkan sistem penomoran lain
dan memiliki lebih banyak jumlah untuk menyajikan situasi yang
berbeda meskipun sistem bilangan Hexadesimal memiliki lebih
representasi tetapi representasi yang dapat mencakup karakter
3
didalamnya juga yang membuat mereka sulit untuk memahami dan
digunakan dengan sistem desimal. Sistem bilangan desimal yang begitu
sering digunakan bahwa seseorang bahkan tidak perlu memiliki
pendidikan formal untuk mengetahui atau menggunakannya.
b. Biner (Basis 2)
Biner (Basis 2) adalah sistem bilangan dasar dua adalah
pengelompokkan unsur dalam suatu himpunan dua-dua. Sistem bilangan
basis dua disebut juga sebagai sistem biner. Lambang bilangan dalam
sistem bilangan dasar dengan basis dua terdapat dua buah yaitu : { 0, 1 }.
Bilangan biner ini dipopulerkan oleh John Von Neumann.
Gambar 1 John Von Neumann
John Von Neumann (Neumann János) (lahir di Budapest,
Hungaria, 28 Desember 1903 – meninggal di Washington DC, Amerika
Serikat, 8 Februari 1957 pada umur 53 tahun) adalah seorang
matematikawan dari Hungaria-Jerman yang memberikan kontribusi
penting di bidang fisika kuantum, analisis fungsional, teori himpunan,
ilmu komputer, ekonomi dan bidang lainnya yang berkaitan dengan
matematika.
4
John Von Neumann diabadikan namanya sebagai arsitektur Von
Neumann, yaitu arsitektur komputer yang banyak digunakan di sebagian
besar sistem komputer non-paralel, karena dialah yang pertama kali
mempublikasikan konsep tersebut.
Contoh sistem biner dapat penggunaannya untuk mewakili bit
dalam komputer yang hanya dapat memiliki 0 atau 1 nilai switch di
sirkuit listrik yang dapat berupa pada (1) atau off (0). Sistem bilangan
biner juga digunakan dalam tabel ASCII untuk mewakili kode yang
berbeda untuk karakter yang berbeda yang kemudian dapat digunakan
dalam komputasi juga. Nomor ASCII lebih seperti kombinasi angka
biner. Bilangan biner juga digunakan dalam alamat IP sistem lagi yang
merupakan kombinasi dari nomor biner dan digunakan dalam bidang
komputasi. Alamat IP ini dari dua versi yang berbeda sekarang salah satu
yang dikenal sebagai IP 4 dan satu lainnya yang dikenal sebagai IP 6.
c. Oktal (Basis 8)
Oktal (Basis 8) adalah sistem bilangan yang terdiri dari 8 simbol
yaitu: { 0, 1, 2, 3, 4, 5, 6, 7 }. Nomor oktal yang tidak umum digunakan
dibandingkan dengan nomor lain dan sebagian besar digunakan dalam
grafis komputer, teks dan sistem operasi terkenal seperti UNIX juga
menggunakan nomor oktal untuk sistem proteksi file mereka. Nomor
oktal
memiliki
total
8
representasi
yang
unik
yang
dapat
dikombinasikan bersama untuk membuat lebih banyak jumlah oktal
representasi. Nomor oktal yang sulit dipahami bagi orang normal yang
memiliki
keterbatasan
jumlah
memahami
tentang
sistem
bilangan. Sebagai setelah 7 nomor yang berbeda digunakan untuk
mewakili angka 7 dan seterusnya dan karenanya mereka tampak secara
fisik agak sulit untuk dipahami. Sistem bilangan perlu menggunakan
subscript 8 dengan nomor untuk mewakili mereka tidak decimal tapi
oktal jumlah dinyatakan kebingungan dapat dengan mudah terjadi.
5
d. Hexadesimal (Basis 16)
Hexadesimal (Basis 16), Hexa berarti 6 dan desimal berarti 10
adalah sistem bilangan yang terdiri dari 16 simbol yaitu 0, 1, 2, 3, 4, 5,
6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15). Pada sistem
bilangan hexsadesimal memadukan 2 unsur yaitu angka dan huruf.
Huruf A mewakili angka 10, B mewakili angka 11 dan seterusnya
sampai huruf F mewakili angka 15. Hexadesimal angka yang banyak
digunakan oleh komputer sitem desainer dan programmer. Hexadesimal
juga isa digunakan untuk mewakili alamat memori komputer. Sistem
hexadesimal biasa digunakan oleh programmer untuk menggambarkan
lokasi di memori. Penggunaan umum dari hexadesimal nomor adalah
untuk menggambarkan warna pada halaman web. Masing-masing dari
tiga warna primer (yaitu, merah, hijau dan biru) diwakili oleh dua digit
hexadesimal untuk membuat 255 nilai yang mungkin, sehingga
mengakibatkan lebih dari 16 juta mungkin warna.
2. Penerapan Teori Bilangan Bulat dalam Bidang Teknologi.
Seiring
dengan
perkembangan
zaman,
maka
munculah
cabang
matematika baru yang disebut dengan matematika diskrit. Perkembangan
yang pesat dari ilmu matematika diskrit ini berkaitan erat dengan
perkembangan pesat dari dunia komputer digital, karena komputer digital
bekerja secara diskrit. Perkembangan matematika diskrit ini juga diikuti
dengan perkembangan ilmu lainnya yang memakai matematika sebagai
landasan ilmunya. Salah satunya adalah ilmu kriptrografi yang memakai
teori bilangan bulat sebagai landasan ilmunya. Dalam matematika diskrit
khusunya teori bilangan bulat memiliki hubungan yang sangat erat
dengan ilmu kriptografi. Selain itu akan dijelaskan pula mengenai
aplikasi dari ilmu keriptografi ini dalam kehidupan sehari-hari.
Kriptografi ini adalah suatu cabang ilmu yang digunakan untuk menjaga
kerahasiaan pesan dengan cara menyamarkannya dan menjadikan bentuk
sandi yang tidak mempunyai makna. Penerapan teori bilangan bulat
dalam kriptografi dan aplikasinya dalam kehidupan sehari-hari yang
6
berupa
deretan
karakter
atau
deretan
bilangan
bulat,
dijaga
kerahasiaannya. Hanya orang yang mengetahui kunci yang dapat
melakukan enkripsi dan deskripsi. Kunci ini analog fungsinya dengan
password pada sistem komputer, PIN pada ATM atau kartu kredit.
Bedanya jika password bertujuan untuk otorisasi akses, maka kunci pada
kriptografi ini digunakan oleh Julius Caesar, kaisar Romawi, untuk
menyandikan pesan uang ia kirim kepada gubernurnya. Pada Caesar
chiper, tiap huruf disubtitusi dengan huruf ketiga berikutnya dari susunan
alfabet. Dalamhal ini kuncinya adalah jumlah pergeseran huruf (yaitu 3).
Tiap huruf alfabet digeser 3 huruf ke kanan
pi : A B C D E F G H I J K L M N O P Q R S T U V W
X Y Z
ci : D E F G H I J K L M N O P Q R S T U V W X Y Z
A B C
Contoh :
Plainteks
: AWASI ASTERIX DAN TEMANNYA OBELIX
Cipherteks
: DZDVL DVWHULA GDQ WHPDQQBA REHOLA
Permulaan tahun 400 SM, tentara Sparta di Yunani menggunakan
Scytale yang terdiri dari kertas panjang dari daun papyrus yang dililitkan
pada sebuah silinder berdiameter tertentu (diameter silinder menentukan
hasil penyandian). Pesan ditulis secara horinzontal, baris perbaris. Bila
kertas dilepas maka huruf akan terlihat acak.
Gambar 2 Scytale
Untuk membaca pesan, penerima harus melilitkan kertas ke silinder yang
diameternya sama persis dengan milik pengirimnya.
7
3. Aplikasi Teori Bilangan Bulat pada Metode Barcode (Kode Baris)
Pada awal perkembangannya, penggunaan kode baris dilakukan
untuk membantu proses pemeriksaan barang-barang secara otomatis pada
pasar-pasar swalayan. Namun, pada saat ini kode baris sudah banyak
digunakan pada kartu identitas, kartu kredit, maupun untuk pemeriksaan
secara otomatis pada perpustakaan.
Gambar 3 Barcode
Pada dasarnya kode baris terdiri atas susunan garis-garis vertikal
hitam (bar) dan putih (spasi) dengan ketebalan yang berbeda-beda. Selain
itu, kode baris juga dapat digambarkan dengan angka 1 untuk
melambangkan garis hitam dan 0 untuk garis putih. Misalnya 0011001
merepresentasikan spasi-spasi-garisgaris-spasi-spasi-garis. Garis-garis ini
digambarkan berderet secara horisontal dan merupakan representasi
karakter-karakter
alpha-numerik
(alphabet
dan
numerik).
Untuk
membantu pembacaan kode baris secara manual, biasanya dicantumkan
juga angka-angka atau huruf-huruf di bawah kode baris tersebut. Fungsi
dari kode baris ini adalah menyimpan data-data spesifik seperti: kode
produksi, tanggal kadaluwarsa, maupun nomor identitas. Tujuan pokok
dari kode baris adalah mengidentifikasi sesuatu dengan memberi label
yang berisi kode baris.
B. Aplikasi Teori Bilangan dalam Bidang Sains
1. Bilangan imajiner dan atau bilangan kompleks ini sering dipakai di
bidang teknik elektro dan elektronika untuk menggambarkan sifat arus
AC (listrik arus bolak-balik) atau untuk menganalisa gelombang fisika.
8
2. Negatif dari logaritma berbasis 10 digunakan dalam kimia untuk
mengekspresikan
konsentrasi
ion
hidronium
(pH).
Contohnya,
konsentrasi ion hidronium pada air adalah pada suhu , sehingga pH-nya
7.
3. Satuan bel (dengan simbol B) adalah satuan pengukur perbandingan
(rasio), seperti perbandingan nilai daya dan tegangan. Kebanyakan
digunakan dalam bidang telekomunikasi, elektronik, dan akustik. Salah
satu sebab digunakannya logaritma adalah karena telingan manusia
mempersepsikan suara yang terdengar secara logaritmik. Satuan Bel
dinamakan untuk mengenang jasa Alexander Graham Bell, seorang
penemu di bidang telekomunikasi. Satuan desibel (dB), yang sama
dengan 0,1 bel, lebih sering digunakan.
4. Skala Richter mengukur intensitas gempa bumi dengan menggunakan
skala logaritma berbasis 10.
5. Dalam
astronomi, magnitudo yang
mengukur
terangnya
bintang
menggunakan skala logaritmik, karena mata manusia mempersepsikan
terang secara logaritmik.
C. Aplikasi Teori Bilangan dalam Bidang Musik
Teori bilangan dalam bidang musik dapat digunakan sebagai simbol not
pada nada. Yaitu bilangan asli yang dimulai dari 1 (satu) sampai 7 (tujuh).
Contohnya, 1= do, 2= re, 3=mi, 4= fa, 5=sol, 6=la, 7=si
D. Aplikasi Teori Bilangan dalam Bidang Filsafat
Filsafat membahas bilangan sebagai objek studi material artinya
filsafat menjadikan bilangan sebagai objek sasaran untuk menyelidiki ilmu
tentang bilangan itu sendiri. Objek material filsafat ilmu bilangan adalah
bilangan itu sendiri. Bilangan itu sendiri dimulai dari yang paling sederhana,
yakni bilangan asli, bilangan cacah, kemudian bilangan bulat, dan
seterusnya hingga bilangan kompleks. Sebagai objek formal filsafat,
bilangan dikaji hakikat. Pengkajian filosofi tentang bilangan misalnya
9
mengenai apa hakikat dari bilangan itu, bagaimana merealisasikan konsep
bilangan yang abstrak menjadi riil atau nyata, bagaimana penggunaan
bilangan untuk penghitungan dan atau pengukuran.
Seperti halnya filosofi pada angka 0. Angka 0 memilki arti dalam diri
dan kehidupan kita. Dengan adanya angka 0, kita dapat mengenal nilai
angka-angka lainnya. Angka 1 akan bernilai lebih besar jika diikuti angka 0
menjadi angka 10. Dalam skala 1-10, angka 10 merupakan nilai yang
sempurna. Angka 0 membuat angka 1 lebih bernilai, dan angka 1 bisa
membuat angka 0 ada nilainya, yaitu 0 satuan. Hal ini menunjukkan arti
bahwa sesuatu memiliki manfaat, dan kebermanfaatan itu bisa dinilai ketika
sesuatu tersebut mampu mengisi kekosongan dan menutupi kekurangan.
Tanpa memahami kekurangan, kita tidak akan menggali dan mencari, serta
memanfaatkan kelebihan kita untuk menutupi kekurangan tersebut. Tidak
akan ada yang sempurna tanpa adanya yang tak sempurna. Nilai manfaat
inilah yang menjadikan sesuatu bermakna dan penting dalam hidup kita
hingga bisa menyirnakan kekosongan tersebut. Jika kita resapi dan kita
hayati, fungsi dan nilai kehidupan kita terletak pada memberi manfaat.
Kebermanfaatan atau kebergunaan kita dimulai untuk diri sendiri, keluarga,
saudara, sahabat, masyarakat, bangsa dan negara serta agama kita
E. Aplikasi Teori Bilangan dalam Bidang Hiburan (Permainan)
1. Ambil tanggal lahir kamu lalu kali 4, hasilnya tambah 13, hasilnya kali
25 lalu kurangi dengan 200, hasilnya tambah dengan bulan lahir kamu
lalu hasilnya kali 2 terus kurangi dengan 40, hasilnya kali dengan 50
hasilnya lagi tambah dengan 2 digit terakhir tahun lahir kamu lalu
hasilnya kurangi dengan 10500..berapa hasilnya?
2. Ambil dua digit terakhir tahun lahir kamu dan tambahkan dengan
umurmu di tahun 2011. Berapa hasilnya? Selalu 111 kan?
3. Coba pilih sesuka hati Anda sebuah bilangan asli (bilangan mulai dari 1
sampai tak hingga). Sebagai contoh, katakanlah 141.985. Kemudian
hitunglah jumlah digit genap, digit ganjil, dan total digit bilangan
10
tersebut. Dalam kasus ini, kita dapatkan 2 (dua buah digit genap), 4
(empat buah digit ganjil), dan 6 (enam adalah jumlah total digit). Lalu
gunakan digit-digit ini (2, 4, dan 6) untuk membentuk bilangan
berikutnya, yaitu 246.
Ulangi hitung jumlah digit genap, digit ganjil, dan total digit pada
bilangan 246 ini. Kita dapatkan 3 (digit genap), 0 (digit ganjil), dan 3
(jumlah total digit), sehingga kita peroleh 303. Ulangi lagi hitung
jumlah digit genap, ganjil, dan total digit pada bilangan 303. (Catatan: 0
adalah bilangan genap). Kita dapatkan 1, 2, 3 yang dapat dituliskan
123. Jika kita mengulangi langkah di atas terhadap bilangan 123, kita
akan dapatkan 123 lagi. Dengan demikian, bilangan 123 melalui proses
ini adalah lubang hitam bagi seluruh bilangan lainnya. Semua bilangan
di alam semesta akan ditarik menjadi bilangan 123 melalui proses ini,
tak satu pun yang akan lolos.
Kesimpulannya,
banyak
sekali
orang
yang
belum
mengetahui
pengaplikasian Teori Bilangan dalam kehidupan sehari-hari. Masih banyak
aplikasi-aplikasi Teori Bilangan yang belum kita ketahui, pemaran diatas hanya
sebagian kecil yang penulis temui. Suatu ilmu akan bermakna bilamana kita
mengetahui pengaplikasiannya atau manfaat penggunaannya.
Manfaat dari essay ini adalah sebagai sarana menambah pengetahuan bagi
pembaca. Dengan membaca essay ini bisa menginspirasi pembaca untuk
mencari tahu mengenai aplikasi-aplikasi lain dari Teori Bilangan.
11
DAFTAR PUSTAKA
Essays, UK. (2013) Number system is used in IT applications. [Online]. Tersedia :
http://www.ukessays.com/essays/social-work/number-system-is-used-in-itapplications-social-work-essay.php. [15 juni 2015]
Qibthiah, M. (2012) Sejarah Teori Bilangan. [Online]. Tersedia : http://mariatulqibthiah.blogspot.nl/p/sejarah-teori-bilangan.html. [1 Juni 2015]
Rangkuti, R.K. (2013) Sejarah Teori Bilangan. Makalah Program Pasca Sarjana
Universitas Negeri Medan. Medan
Rinaldi, M. (2013) Teori Bilangan. PPT Teori Bilangan.
Suryanti, N. (2012) Sejarah Teori Bilangan. [ Online]. Tersedia :
https://matematikaoye.wordpress.com/sejarah-teori-bilangan-3/. [1 Juni
2015]
Wikipedia.
(2015)
Hexadesimal.
[Online].
Tersedia
:
https://en.m.wikipedia.org/wiki/Hexadecimal. [15 Juni 2015]