KONDUKTOR dan DIELEKTRIK

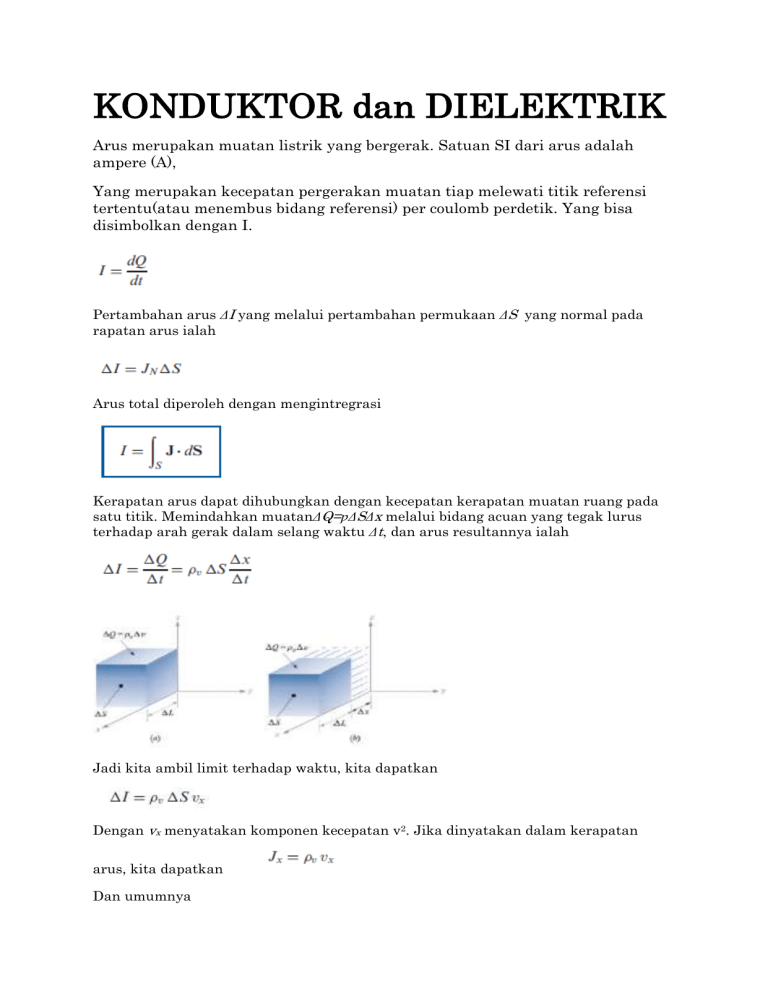
KONDUKTOR dan DIELEKTRIK
Arus merupakan muatan listrik yang bergerak. Satuan SI dari arus adalah
ampere (A),
Yang merupakan kecepatan pergerakan muatan tiap melewati titik referensi
tertentu(atau menembus bidang referensi) per coulomb perdetik. Yang bisa
disimbolkan dengan I.
Pertambahan arus ΔI yang melalui pertambahan permukaan ΔS yang normal pada
rapatan arus ialah
Arus total diperoleh dengan mengintregrasi
Kerapatan arus dapat dihubungkan dengan kecepatan kerapatan muatan ruang pada
satu titik. Memindahkan muatanΔQ=ƿΔSΔx melalui bidang acuan yang tegak lurus
terhadap arah gerak dalam selang waktu Δt, dan arus resultannya ialah
Jadi kita ambil limit terhadap waktu, kita dapatkan
Dengan vx menyatakan komponen kecepatan v2. Jika dinyatakan dalam kerapatan
arus, kita dapatkan
Dan umumnya

Konduktor
Sebuah konduktor memiliki limpahan muatan yang bebas untuk bergerak. Jika sebuah
konduktor terisolasi, seperti yang ditunjukkan pada Gambar 1(a). Ketika medan listrik
eksternal Ee diterapkan, muatan bebas positif didorong sepanjang arah yang sama
dengan medan listrik, sedangkan untuk muatan bebas negatif bergerak dalam arah
yang berlawanan. Perpindahan muatan ini berlangsung sangat cepat. Muatan bebas
biasanya melakukan dua hal. Pertama, mereka menumpuk di permukaan konduktor
dan membentuk muatan permukaan induksi. Kedua, muatan induksi membentuk
sebuah bidang induksi didalam medan Ei, dimana membatalkan muatan eksternal
yang diterapkan pada medan Ee. Hasilnya diilustrasikan pada Gambar 1(b). Ini
mengarah ke sifat penting dari konduktor yaitu :
Sebuah konduktor sempurna tidak mempunyai medan elektrostatik di dalamnya.
Sebuah konduktor disebut badan ekipotensial, menyiratkan bahwa potensi adalah sama
di mana-mana dalam konduktor. Hal ini didasarkan pada kenyataan bahwa E = – = 0.
Cara lain untuk melihat ini adalah dengan mengacu pada hukum Ohm, J = σE. Untuk
mempertahankan kuat arus terbatas J, dalam sebuah konduktor sempurna (σ à ∞),
mensyaratkan bahwa medan listrik di dalam konduktor harus dihilangkan. Dengan
kata lain, E à 0 karena σ à ∞ dalam sebuah konduktor sempurna. Jika beberapa
muatan dimasukkan di bagian dalam konduktor tersebut, muatan akan bergerak ke
permukaan dan terdistribusi sendiri dengan cepat dan dengan sedemikian rupa bahwa
medan di dalam konduktor hilang. Menurut hukum Gauss, jika E = 0, kuat
muatan Pv harus nol. Dan dapat disimpulkan lagi bahwa konduktor yang sempurna
tidak mempunyai medan elektrostatik,
Gambar 1(a) Konduktor terisolasi di bawah pengaruh suatu medan listrik, (b)
konduktor memiliki medan listrik nol dalam kondisi statis
Berdasarkan hukum Ohm
,
kita akan memperoleh resistansi dari bahan hantaran. Misalkan konduktor memiliki
penampang seragam S dan panjang €. Arah medan listrik E yang dihasilkan adalah
sama dengan arah aliran muatan positif atau arus I. Arah ini berlawanan dengan arah
aliran elektron. Medan listrik yang digunakan adalah seragam dan besarnya yaitu :
Sejak konduktor memiliki penampang yang seragam, dengan mensubtitusikan kedua
persamaan diatas kedalam persamaan ke persamaan di bawah ini
m
aka akan menghasilkan sebuah persamaan:
Ole
h karena itu :
atau
(2)
SEMIKONDUKTOR
• Germanium, silikon dan selinium adalah contoh material semikonduktor
• Pembawa arus dalam material semikonduktor adalah elektron dan hole
• Mobilitas elektron dan hole pada silikon berturut-turut 0,12 dan 0,025
• Mobilitas elektron dan hole dari germanium berturut-turut 0,36 dan 0,17
• Konsentrasi elektron dan hole pada bahan tergantung pada temperatur
• Pada 300K, kerapatan muatan volume elektron dan hole untuk silikon adalah0,0024
C/m3 dan 3,0 C/m3 sedangkan untuk germanium adalah
• Rumus konduktivitas semikonduktor :
Sifat Bahan Dielektrik
• Dielektrik dalam medan listrik dapat dipandang sebagai susunan dwikutub
mikroskopik dalam ruang hampa yg terdiri dari muatan positif dan negatif
yang pusatnya tidak berimpit
• Muatan tsb bukan muatan bebas (terikat oleh gaya atomik dan molekular) dan tak
memberikan proses konduksi
• Dielektrik gas, cair, padat (kristal/bukan) memiliki kemampuan menyimpan
energilistrik
• Penyimpanan ini terjadi krn pergeseran relatif kedudukan dwikutub. Pergeseran ini
dapat menimbulkan gejala transien
• Sumber energinya adalah medan eksternal
• Bahan dielektrik polar (berkutub) mempunyaipergeseran yang permanen antara pusat muatan
positif dan pusat muatan negatif
• Molekul tak berkutub (nonpolar) tidak mempunyai susunan dwikutub sebelum medan eksternal
dikenakan padanya
• Kekuatan pergeseran dwikutub dalam bahan dielektrik diukur dengan P (polarisasi)
Kapasitansi
Kapasitansi atau kapasitans adalah ukuran jumlah muatan listrik yang disimpan (atau dipisahkan)
untuk sebuah potensial listrik yang telah ditentukan. Bentuk paling umum dari piranti penyimpanan
muatan adalah sebuah kapasitor dua lempeng/pelat/keping. Jika muatan di lempeng/pelat/keping
adalah +Q dan –Q, dan V adalah tegangan listrik antar lempeng/pelat/keping, maka rumus
kapasitans adalah:
C adalah kapasitansi yang diukur dalam Farad
Q adalah muatan yang diukur dalam coulomb
V adalah voltase yang diukur dalam volt
Unit SI dari kapasitansi adalah farad; 1 farad = 1 coulomb per volt.
Energi
Energi (diukur dalam satuan joule) yang disimpan dalam sebuah kapasitor sama dengan kerja yang
telah dilakukan untuk mengisinya dengan muatan listrik. Anggap sebuah kapasitans sebagai C, yang
menyimpan muatan +q di sebuah lempeng dan -q di lempeng yang lain. Memindahkan sebuah
elemen muatan yang kecil
dari satu lempeng ke lempeng yang lain bertentangan dengan beda
potensial V = q/C memerlukan kerja
:
dimana
W adalah kerja yang diukur dalam joule
q adalah muatan yang diukur dalam coulomb
C adalah kapasitans yang diukur dalam farad
Kita bisa mengetahui energi yang tersimpan dalam sebuah kapasitas
dengan mengintegralkan persamaan ini. Dimulai dengan sebuah kapasitans tak bermuatan (q=0) dan
memindahkan muatan dari satu lempeng ke lempen yang lain sampai lempeng bermuatan +Q dan Q membutuhkan kerja W:
Dengan mengombinasikan persamaan di atas untuk kapasitansnya sebuah kapasitor pelat rata, kita
mendapatkan:
.
Kapasitor plat sejajar
Tapi coba kalau kita balik nanya, dari mana sih asal rumus kapasitansi kapasitor plat sejajar yang
punya persamaan:
Ok, sebelum kita membahas tentang kapasitor plat sejajar lebih jauh, gimana kalau kita kenalan dulu
sama yang namanya persamaan hukum Gauss untuk medan listrik. Hukum Gauss untuk medan listrik
itu adalah salah satu dari 4 persamaan Maxwell yang luar biasa banget itu. Isinya untuk yang
tampilan integral adalah:
Namun sebagai catatan, medan listrik dalam kapasitor plat sejajar itu kita ambil medan listrik yang
ideal aja, atau yang tegak lurus karena kita anggap kapasitor plat sejajar memiliki luasan yang tak
hingga. Nilai d (jarak antar kepingnya)-nya jauh lebih kecil dibandingkan A (luas)-nya. Atau kalau
dibandingkan kayak gambar di bawah ini, dan kita menggunakan yang A. Ya, sebenernya sih ini untuk
mempermudah kita bekerja dibandingkan kalau kita ngerjain sistem yang B (yang real kapasitor)
Kalau kita perhatiin dalam persamaan 1 Maxwell atau dalam hukum Gauss untuk medan listrik itu
kan persamaannya kayak gini:
Jadi, kalau kita selesaiin sistem itu maka jadinya adalah:
Dengan σ itu adalah rapat muatan per satuan luas. Atau mungkin kita lebih nyaman sama tampilan
yang seperti ini ya.
Sehingga
Q = E.A.ε
Ocre, kita kan udah nemu tuh persamaan untuk medan listrik di dalam kapasitor. Sekarang gimana
kalau kita nyari nilai potensialnya ya.. Inget kan, hubungan E sama V adalah:
V = E.d
Dimana nilai d itu berarti kalau dalam keeping sejajar adalah jarak antar kepingnya. Jadi kalau kita
masukin ke dalam persamaan kapasitansi jadinya adalah:
C = Q/V
Jadi,
Sehingga:
Jadi sebenarnya ε itu adalah permitivitas bahan atau suatu sifat elektrik dari suatu bahan. Nah,
kalau ε0 itu adalah nilai permitivitas dalam ruang hampa. So, yang kita temuin dari hukum Gauss itu
adalah rumus umum dari kapasitas kapasitor tanpa menentukan nilai permitivitasnya. Dalam artian,
kita bisa gunakan semua bahan dalam persamaan tersebut ga perlu menentukan apakan itu ruang
hampa atau bukan. Sedangkan kalau yang ada di atas banget itu, itu hanya berlaku kalau kapasitor
menggunakan bahan ruang hampa sebagai bahan dielektriknya.
Sehingga, dengan menggunakan persamaan kapasitansi itu kita bisa menentukan jenis bahan yang
terdapat antara keping sejajarnya. Dan aplikasi ini memungkinkan kita untuk menghitung kadar air
dalam suatu bahan atau menentukan jenis bahan berdasarkan karakteristik permitivitasnya.