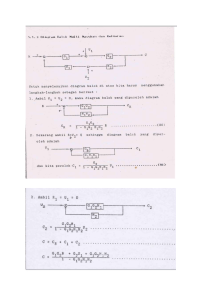
FUNGSI ALIH Fungsi Alih / Transfer Fungsi adalah perbandingan output terhadap input (Fungsi awal Nol) 𝐺(𝑠) = £output £input 𝐺(𝑠) = Y(s) X(s) DIAGRAM BLOK 1. Fungsi Alih Sistem Loop Tertutup (Diagram Blok mbah) 2. Fungsi Alih Loop Terbuka Gambar Fungsi Alih Sistem Loop Tertutup tidak ada feed back, dimana H(s) sejajar dengan G (s) B(s) E(s) = 𝐺(𝑠). 𝐻(𝑠) 3. Fungsi Alih Lintasan Maju Gambar Fungsi Alih Sistem Loop Tertutup, hanya ada lintasan maju dan tidak ada feed back, H(s) hilang dan yang ada G (s) C(s) E(s) 4. Fungsi Alih Loop Tertutup = 𝐺(𝑠) C(s) = G(s).E(s) E(s) = R(s) – B(s) = R(s) – H(s).C(s) Jadi C(s) = G(s). [ R(s) – H(s).C(s)] C(s) = G(s).R(s) – G(s).H(s).C(s); dimana G(s).H(s).C(s) adalah negative dan disimpan sebelah kiri sama dengan sehingga menajdi positif C(s) + G(s).H(s).C(s) = G(s).R(s) C(s) [ 1 + G(s).H(s) ] = G(s).R(s) Sehingga didapatkan ( rumus mbah ) 𝑪(𝒔) 𝑮(𝒔) = 𝑹(𝒔) 𝟏 + 𝑮(𝒔). 𝑯(𝒔) Langkah-langkah penyelesaian Blok Diagram Contoh soal 1 1. Gambar 1 adalah gambar blok diagram tidak bisa diselesaikan (sesuai blok diagram mbah), karena titik percabangan H2 ada berada diantara G3 dan G4 2. Pada gambar 2 /a, Pindahkan titik percabangan H2 setelah G4 dan terjadi perubahan H2 menjadi (H2/G4). Sehingga didapatkan blok diagram kecil pertama didalam lingkaran besar yakni G3, G4 dan H1 (semua positif). a. Karena G3 dan G4 sejajar/seri maka : Gt1 = G3 . G4 b. berlaku rumus mbah, dimana Gt1 = G(s) dan H1 = H(s), sehingga didapatkan : 𝐺𝑡1 𝐺𝑡2 = 1− 𝐺𝑡1.𝐻1 = 3. 𝐺3.𝐺4 1−𝐺3.𝐺4.𝐻1 Pada gambar 3/b, terdapat G2, Gt2 dan (H2/G4). a. G2 dan Gt2 sejajar/seri maka : Gt3 = G2 . Gt2; sehingga didapatkan 𝐺𝑡3 = 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 = 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 b. berlaku rumus mbah, dimana Gt3 = G(s) dan - (H2/G4) = H(s), sehingga didapatkan : 𝐺𝑡4 = 𝐺2. 𝐺3. 𝐺4 𝐺𝑡3 𝐻2 1 + 𝐺𝑡3. ( ) 𝐺4 = 1+ 𝐺2. 𝐺3. 𝐺4 𝐺𝑡4 = 𝐺2. 𝐺3. 𝐺4 𝐻2 .( ) 1 − 𝐺3. 𝐺4. 𝐻1 𝐺4 𝐺2. 𝐺3. 𝐺4 (1 − 𝐺3. 𝐺4. 𝐻1) 1+ (1 − 𝐺3. 𝐺4. 𝐻1) 𝐺2. 𝐺3. 𝐻2 . 1 − 𝐺3. 𝐺4. 𝐻1 (1 − 𝐺3. 𝐺4. 𝐻1) = 1 − 𝐺3. 𝐺4. 𝐻1 𝐺2. 𝐺3. 𝐻2 + . 1 − 𝐺3. 𝐺4. 𝐻1 1 − 𝐺3. 𝐺4. 𝐻1 𝐺2. 𝐺3. 𝐺4 (1 − 𝐺3. 𝐺4. 𝐻1) 𝐺𝑡4 = 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1 − 𝐺3. 𝐺4. 𝐻1 𝐺𝑡4 = ( 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 𝐺𝑡4 = ( ).( 1 − 𝐺3. 𝐺4. 𝐻1 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 ) ) 4. Gambar 4/c, terdapat G1, Gt4 dan H3 a. G1 dan Gt4 sejajar/seri maka : Gt5 = G1 . Gt4; sehingga didapatkan 𝐺2. 𝐺3. 𝐺4 𝐺𝑡5 = 𝐺1. ( 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 ) = ( 𝐺1. 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 ) b. berlaku rumus mbah, dimana Gt5 = G(s) dan – (H3) = H(s), sehingga didapatkan : 𝐺𝑡6 = 𝐺1. 𝐺2. 𝐺3. 𝐺4 𝐺𝑡5 1 + 𝐺𝑡3. 𝐻3 (1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) = 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 ) 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1+( 𝐺1. 𝐺2. 𝐺3. 𝐺4 ) 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺𝑡6 = 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 (1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) + (1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) ( 𝐺1. 𝐺2. 𝐺3. 𝐺4 (1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) 𝐺𝑡6 = 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 + 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 ( ) 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺𝑡6 = 𝐺1. 𝐺2. 𝐺3. 𝐺4 𝑥 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 + 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 𝐺𝑡6 = 𝐺1. 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 + 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 5. Gambar 5/d adalah Fungsi Alih, sehingga didapat loop kalang terbuka 𝐺(𝑠) = 𝐶(𝑠) 𝑅(𝑠) = 𝐺1. 𝐺2. 𝐺3. 𝐺4 1 − 𝐺3. 𝐺4. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 + 𝐺1. 𝐺2. 𝐺3. 𝐺4. 𝐻3 Langkah-langkah penyelesaian Blok Diagram Contoh soal 2 1. Gambar a adalah gambar blok diagram tidak bisa diselesaikan (sesuai blok diagram mbah), karena H2 berada pada titik penjumlahan ketiga, yang berada diantara G1 dan G2. 2. Pada gambar b, Pindahkan H2 yang berada pada titik penjumlahan ketiga ke titik penjumlahan kedua dan terjadi perubahan H2 menjadi (H2/G1) karena melompati G1. Sehingga didapatkan blok diagram kecil pertama didalam lingkaran besar yakni G 1, G2 dan H1 (semua positif). a. Karena G1 dan G2 sejajar/seri maka : Gt1 = G1 . G2 b. berlaku rumus mbah, dimana Gt1 = G(s) dan H1 = H(s), sehingga didapatkan : 𝐺𝑡1 𝐺𝑡2 = 1− 𝐺𝑡1.𝐻1 = 3. 𝐺1.𝐺2 1−𝐺1.𝐺2.𝐻1 Pada gambar c, terdapat G3, Gt2 dan - (H2/G1). a. G3 dan Gt2 sejajar/seri maka : Gt3 = G3 . Gt2; sehingga didapatkan 𝐺𝑡3 = 𝐺3. 𝐺1. 𝐺2 1 − 𝐺1. 𝐺2. 𝐻1 = 𝐺1. 𝐺2. 𝐺3 1 − 𝐺1. 𝐺2. 𝐻1 b. berlaku rumus mbah, dimana Gt3 = G(s) dan - (H2/G1) = H(s), sehingga didapatkan : 𝐺𝑡4 = 𝐺1. 𝐺2. 𝐺3 𝐺𝑡3 𝐻2 1 + 𝐺𝑡3. ( ) 𝐺1 (1 − 𝐺1. 𝐺2. 𝐻1) = 1+ 𝐺1. 𝐺2. 𝐺3. 𝐻2 .( ) 1 − 𝐺1. 𝐺2. 𝐻1 𝐺1 𝐺1. 𝐺2. 𝐺3 𝐺𝑡4 = (1 − 𝐺1. 𝐺2. 𝐻1) 1+ 𝐺2. 𝐺3. 𝐻2 . 1 − 𝐺1. 𝐺2. 𝐻1 𝐺1. 𝐺2. 𝐺3 (1 − 𝐺1. 𝐺2. 𝐻1) 𝐺𝑡4 = 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1 − 𝐺1. 𝐺2. 𝐻1 𝐺𝑡4 = ( 𝐺1. 𝐺2. 𝐺3 = (1 − 𝐺1. 𝐺2. 𝐻1) 1 − 𝐺1. 𝐺2. 𝐻1 𝐺2. 𝐺3. 𝐻2 + . 1 − 𝐺1. 𝐺2. 𝐻1 1 − 𝐺1. 𝐺2. 𝐻1 𝐺1. 𝐺2. 𝐺3 1 − 𝐺1. 𝐺2. 𝐻1 = ( ). ( ) 1 − 𝐺1. 𝐺2. 𝐻1 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 . 𝐺1. 𝐺2. 𝐺3 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 ) 4. Gambar d, terdapat Gt4 dan 1 berlaku rumus mbah, dimana Gt4 = G(s) dan 1 = H(s), sehingga didapatkan : 𝐺𝑡5 = 𝐺1. 𝐺2. 𝐺3 𝐺𝑡4 1 + 𝐺𝑡4. (1) = (1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) 𝐺1. 𝐺2. 𝐺3 ) 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1+( 𝐺1. 𝐺2. 𝐺3 (1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) 𝐺𝑡5 = 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺1. 𝐺2. 𝐺3 (1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) + (1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) 𝐺1. 𝐺2. 𝐺3 (1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2) 𝐺𝑡5 = 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻 + 𝐺1. 𝐺2. 𝐺3 ( ) 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 𝐺𝑡5 == ( 𝐺1. 𝐺2. 𝐺3 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 ) .( 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻2 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻 + 𝐺1. 𝐺2. 𝐺3 𝐺1. 𝐺2. 𝐺3 𝐺𝑡5 = ( 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻 + 𝐺1. 𝐺2. 𝐺3 5. ) Gambar e adalah Fungsi Alih, sehingga didapat loop kalang terbuka 𝐺(𝑠) = 𝐶(𝑠) 𝑅(𝑠) = ( 𝐺1. 𝐺2. 𝐺3 1 − 𝐺1. 𝐺2. 𝐻1 + 𝐺2. 𝐺3. 𝐻 + 𝐺1. 𝐺2. 𝐺3 ) )