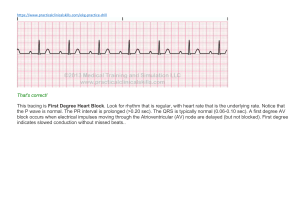
GRAPHING MOTION VIRTUAL LAB 2 AP PHYSICS 1 Name: _________________________________ Date: __________________________________ FORMATIVE GRADE ⌂ WEIGHT = 1 DIRECTIONS: Run http://www.thephysicsaviary.com/Physics/Programs/Labs/GraphingOfMotionLab/index.html And generate the following velocity vs. time graph. Answer the questions following. Now that you know your formulas for distance, velocity, and acceleration, answer the following questions below: 1. Find the distances travelled by the car in the following time intervals: Time interval Distance travelled (in m) 0 ≤ t ≤ 5 sec 5 ≤ t ≤ 7.5 sec 7.5 ≤ t ≤ 12 sec 12 ≤ t ≤ 19 sec 19 ≤ t ≤ 25 sec 25 ≤ t ≤ 30 sec 2. Find the formulas for velocity vs. time for each of the six segments above. Make the leftmost value of time zero and adjust when coming up with each new velocity formula. Time interval 0 ≤ t ≤ 5 sec Velocity V = 12 vs. time formula 5 ≤ t ≤ 7.5 sec (0 ≤ t ≤ 2.5 sec) Vf = 12 – (7/2.5)t 7.5 ≤ t ≤ 12 sec (0 ≤ t ≤ 5.5 sec) 12 ≤ t ≤ 19 sec (0 ≤ t ≤ 7 sec) 19 ≤ t ≤ 25 sec (0 ≤ t ≤ 6 sec) 25 ≤ t ≤ 30 sec (0 ≤ t ≤ 5 sec) 3. Graph (not sketch) d vs. t below. Label the pivotal points in the graph that correspond with the original graph above. The pivotal points are the six places where the graph changes behavior. 1000 900 800 700 600 500 400 300 200 100 4. Find the formula for distance vs. time for each of the six segments above. Make the leftmost value of time zero and adjust when coming up with each new velocity formula. Time interval 0 ≤ t ≤ 5 sec Distance vs. time formula Time interval 5 ≤ t ≤ 7.5 sec (0 ≤ t ≤ 2.5 sec) Distance vs. time formula Time interval 7.5 ≤ t ≤ 12 sec (0 ≤ t ≤ 5.5 sec) Distance vs. time formula Time interval 12 ≤ t ≤ 19 sec (0 ≤ t ≤ 7 sec) Distance vs. time formula Time interval 19 ≤ t ≤ 25 sec (0 ≤ t ≤ 6 sec) Distance vs. time formula Time interval 25 ≤ t ≤ 30 sec (0 ≤ t ≤ 5 sec) Distance vs. time formula 5. Graph (not sketch) a vs. t below. Label the pivotal points in the graph that correspond with the six segments of the original graph above. The pivotal points are where the graph changes behavior. 10 8 6 4 2 0 -2 -4 -6 -8 -10