Metode Biseksi

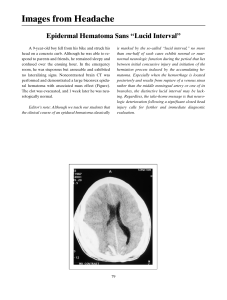
Bisection
Method
ꟷNon Linear Equation
Introduction of Bisection Method
The Bisection Method give a proof of a
practical method to find roots of
equations by “bi section”.
Bisection Method is formulated
based on prior theories and has been
stated as “ f (x) be a continuous function on
the interval [a, b]. If f (a) and f (b)
have opposite signs, then there is
an 𝛼 ∈ [a, b] such that f (𝛼) = 0
with a < 𝛼 < b”.
There will be 3 possibilities from this equation :
• If 𝑓 𝑎0 . 𝑓 𝑥0 < 0, the root lies in 𝑎0 and 𝑥0
• If 𝑓 𝑏0 . 𝑓 𝑥0 > 0, there is no root lies in 𝑥0
and 𝑏0
• If 𝑓(𝑥0 ) = 0, we’re already done since 𝑥0 is the
root of 𝑓 𝑥 .
Root 𝛼
The value of 𝛼 can be approximation with midpoint
equation of interval [a0 , b0] ;
a0 + b 0
𝑥𝑜 =
2
* assume that f (a) < 0, while
f (b) > 0, the other case being
handled similarly.
©First Group | Numeric Method | Mathematics Airlangga
University 2019
The red line shows the interval [an, bn].
For an example, we have made an C++
program to determine roots from the equation
©First Group | Numeric Method | Mathematics Airlangga
University 2019