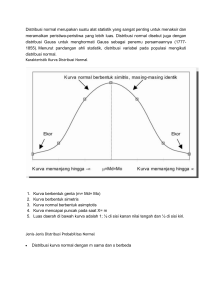
Siapa itu Gauss? Carl Friedrich Gauss (1777-1855) adalah seorang matematikawan berkebangsaan Jerman yang mempunyai kontribusi besar didalam bidang geometri, teori bilangan, teori fungsi dan teori probabilitas. Dia menemukan cara untuk menghitung lintasan asteroid, membuat penemuan dasar di dalam teori potensial (bidang elektromagnetik), dan orang pertama yang menggunakan telegraf (1833). Karena konstribusinya itu, dia mempunyai julukan “Prince of Mathematics”. Eliminasi Gauss Eliminasi gauss ditemukan oleh Carl Friedrich Gauss, metode ini dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan merepresentasikan (mengubah) menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk Eselon Baris melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik. Lalu apa itu eselon baris? dan bagaimana bentuknya? Bentuk Eselon Baris Suatu matriks memiliki bentuk eselon baris jika memenuhi 3 kriteria berikut : 1. Jika didalam baris terdapat elemen-elemen yang tidak semuanya nol, maka bilangan tak nol pertama di dalam baris tersebut adalah 1. Contoh : (Perhatikan setiap baris pada matriks berikut) Dari matriks diatas baris merah dan baris hijau memenuhi kriteria pertama, karena elemen-elemen pada baris merah atau hijau tidak semuanya nol dan bilangan (elemen) bukan nol pertama (dari kiri) di dalam baris tersebut adalah 1. Sedangkan pada baris biru tidak memenuhi kriteria pertama sebab bilangan (elemen) bukan nol pertama (dari kiri) bukan bernilai 1, melainkan bernilai -1. 2. Nah kalau ada baris-baris yang semua elemennya bernilai 0 semua, maka baris-baris tersebut harus dikelompokkan dan diletakkan dibagian bawah matriks. Contoh : Dari contoh diatas, matriks dengan elemen berwarna biru memenuhi kriteria kedua sebab terdapat baris yang semua elemennya 0 dan baris tersebut diletakkan di bagian bawah matriks. Sedangkan pada matriks berwarna merah, masih belum memenuhi kriteria kedua, sebab walaupun terdapat baris dengan elemen-elemennya 0, namun baris-baris tersebut tidak dikelompokkan dan tidak diletakkan di bagian bawah matriks tersebut. Pada matriks merah agar memenuhi kriteria kedua seharusnya : 3. Jika terdapat dua baris berurutan yang memenuhi kriteria pertama, maka angka 1 (pertama/utama) dari baris yang lebih rendah berada lebih kekanan dari angka 1(pertama/utama) baris yang diatasnya. Contoh : Pada matriks hijau sudah memenuhi kriteria ketiga, karena jelas angka 1 pertama (dari kiri) pada baris yang lebih rendah letaknya lebih kekanan dari angka 1 pertama dari baris yang diatasnya. Sedangkan pada matriks biru belum memenuhi sebab terdapat dua baris berurutan yang melanggar kriteria ketiga yaitu baris ke 2 dan 3. Dimana angka 1 pertama baris ketiga terletak tepat di bawah angka 1 pertama baris kedua. Setelah memahami ketiga kriteria (syarat) dari bentuk eselon baris. Berikut contoh matriks yang mempunyai bentuk eselon baris (memenuhi ketiga kriteria sekaligus). 4. Sifat ke-4 ini merupakan sifat khusus yaitu setiap kolom yang mengandung 1 utama maka elemen-elemen lain selain 1 utama bernilai nol. Berikut contoh matriks eselon baris tereduksi yang memenuhi keempat syarat di atas : Selanjutnya kita akan menerapkan metode eliminasi gauss dan subtitusi balik untuk memecahkan suatu sistem persamaan linear dengan operasi baris elementer. Disarankan sudah memahami penggunaan operasi baris elementer untuk pemecahan sistem persamaan linear. Pemecahan SPL dengan Eliminasi Gauss Gambaran diatas merupakan ilustrasi proses pemecahan Sistem Persamaan Linear (SPL), dimana urutan langkah-langkahnya dinamakan “Eliminasi Gauss” dan operasi yang dilakukan dinamakan “Operasi Baris Elementer (OBE)” dimana eliminasi gauss ini bertujuan membentuk Eselon Baris. Catatan : Pada proses pemecahan dengan metode eliminasi gauss pada umumnya memiliki macam-macam jalur atau alur operasi yang dilakukan, misalkan pada langkah awal bisa saja kita menemukan beberapa operasi alternatif dan kita bebas memilihnya. Karena terdapat banyak jalur atau alur operasinya maka jika anda mencoba dengan jalur lain (tidak seperti di contoh) kemungkinan anda akan menemukan bentuk sistem/matriks yang berbeda. Namun jangan khawatir selama operasi yang dilakukan menggunakan Operasi Baris Elementer dan dilakukan secara teliti, maka solusi(pemecahan) yang didapat akan sama dan itu merupakan hal yang wajar. Contoh 1 (Solusi Tunggal) Diberikan sistem persamaan linear sebagai berikut : 2x+5y+3z =12x+5y+3z=1 3x+4y+2z=-33x+4y+2z=−3 x+3y+z=2x+3y+z=2 Perintah : Tentukan pemecahan sistem persamaan linear di atas dengan metode eliminasi gauss. Penyelesaian : Mula-mula kita representasikan sistem tersebut kedalam bentuk matriks. Langkah 1 Kita akan membuat 1 pertama pada baris pertama dengan beberapa pilihan operasi : Langkah 2 Langkah 3 Langkah 4 Langkah 5 Contoh 2 (Banyak Solusi) Diberikan sistem persamaan linear sebagai berikut : 2x+10y+4z =-22x+10y+4z=−2 x+4y+5z=-3x+4y+5z=−3 3x+15y+6z=-33x+15y+6z=−3 Perintah : Tentukan pemecahan sistem persamaan linear di atas dengan metode eliminasi gauss. Penyelesaian : Kita representasikan kedalam bentuk matriks : Langkah 1 Langkah 2 Langkah 3 Contoh 3 (Tidak Punya Solusi) Diberikan sistem persamaan linear sebagai berikut : 3x+12y+15z=63x+12y+15z=6 2x+8y+10z=-62x+8y+10z=−6 4x+5y-6z =-24x+5y−6z=−2 Perintah : Tentukan pemecahan (bila ada) dari sistem persamaan linear di atas dengan metode eliminasi gauss. Penyelesaian : Seperti biasa kita representasikan dulu ke dalam bentuk matriks. Langkah 1 Langkah 2 Karena kontradiksi (berlawanan) dengan pernyataan persamaan (2), akibatnya persamaan (2) tidak mempunyai solusi. Karena persamaan (2) bagian dari sistem persamaan linear tersebut maka sistem persamaan linear tersebut juga tidak punya solusi. Mengingat kembali jika sistem persamaan linear awal (pada soal) dikenakan operasi baris elementer maka akan menghasilkan sistem persamaan linear baru yang memiliki pemecahan yang sama. Baca kembali : Pemecahan Sistem Persamaan Linear dengan Operasi Baris Elementer. Penerapan Eliminasi Gauss-Jordan Eliminasi gauss-jordan akan lebih terasa bermanfaat jika sistem persamaan linear tersebut terdiri dari banyak persamaan dan variabel, semisal sistem tersebut mempunyai 5 persamaan dan 5 variabel di dalamnya. Selain itu, eliminasi gauss dan eliminasi gaussjordan juga dapat diterapkan pada sistem persamaan taklinear tertentu (lihat pada contoh ke-2). Sebenarnya pemecahan SPL dengan metode eliminasi gauss-jordan sudah diterapkan pada postingan sebelumnnya, yaitu pada materi Pemecahan SPL dengan Operasi Baris Elementer yang mana terdapat 3 contoh unik (solusi tunggal, banyak solusi dan tidak punya solusi). Ketiga contoh tersebut dikerjakan dengan prosedur eliminasi gauss-jordan yang dilakukan secara jelas dan runtut. Sehingga sekarang agar lebih menarik kita akan mencoba variasi soal yang lebih unik. Contoh 1 (Linear) Diberikan sistem persamaan linear sebagai berikut : x+2y-3z=4x+2y−3z=4 3x-y+5z=23x−y+5z=2 4x+y+(k^2 -14)z=k+24x+y+(k2−14)z=k+2 Tentukan nilai kk agar SPL di atas : 1. Tidak mempunyai penyelesaian; 2. Tepat mempunyai satu penyelesaian; 3. Mempunyai tak hingga banyak penyelesaian; Penyelesaian : Pertama kita representasikan sistem persamaan linear tersebut kedalam bentuk matriks : Langkah 1 Langkah 2 Langkah 3 Kasus 2 Kesimpulan Contoh 2 (Tak Linear) Untuk membedakan sistem persamaan linear dengan sistem persamaan tak linear, bisa baca kembali Penjelasan Mengenai SIstem Persamaan Linear. Penyelesaian : Kalau kita perhatikan bentuk sistem persamaan tak linear di atas tidak beda jauh dengan sistem persamaan linear yang biasa kita kenal, sehingga jika kita representasikan kedalam bentuk matriks akan diperoleh : Langkah 1 Langkah 2 Langkah 3 Langkah 4 Jika kita perhatikan bentuk terakhir matriks di atas sudah memenuhi bentuk eselon baris, selanjutnya kita akan mengubahnya menjadi eselon baris tereduksi.