SOP and POS - Jaenal Arifin S.T., M.Eng
advertisement

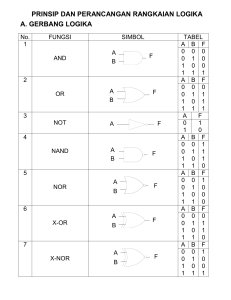
SUM OF PRODUCT, PRODUCT OF SUM DAN RANGKAIAN ARITMATIKA Bentuk SOP dan POS 1. SOP (Sum Of Product) -bentuk pernyataan dikatakan SOP bila semua perkalian yang ada merupakan perkalian variabel tunggal. -mudah dikenali karena pernyataan tesb terdiri atas suku2 penjumlahan dari perkalian. -untuk mendapatkan bentuk SOP, gunakan hukum kedua distributif. 2 Bentuk SOP dan POS Contoh : AC’ + B’DE + AB’E AB’D + BEFG + H (A+B)C’D + E’F bukan SOP - bentuk SOP selalu dapat direalisasikan langsung dengan satu atau lebih gerbang OR pada keluarannya. 3 Bentuk SOP dan POS 2. POS (Product of Sum) -bentuk pernyataan dikatakan memiliki bentuk POS bila semua penjumlahan merupakan penjumlahan variabel tunggal. -mudah dikenali karena pernyataan tersebut terdiri dari suku2 perkalian dari penjumlahan 4 Bentuk SOP dan POS Contoh : (A+B’)(C’+D+E)(A’+C+E) (A+B’)(C+D’+E)F ABC’(D+E’) (A+B’)(C+D’)+EF bukan POS - bentuk POS selalu dapat direalisasikan langsung dengan satu atau lebih gerbang AND pada keluarannya. 5 Gerbang Logika Yang Lain NOR (not OR) 74LS02 A Z B Notasi Z=(A+B)’ Z=(A+B) A B Z 0 0 1 0 1 0 1 0 0 1 1 0 6 Gerbang Logika Yang Lain EXOR (exclusive OR) 74LS86 A Z B Notasi Z=A’B+AB’ Z=A + B A B Z 0 0 0 0 1 1 1 0 1 1 1 0 7 Gerbang Logika Yang Lain EXNOR (exclusive not OR) Notasi Z=A’B’+AB Z=A + B 74LS266 A Z B A B Z 0 0 1 0 1 0 1 0 0 1 1 1 8 Gerbang Logika Yang Lain EXNOR (exclusive not OR) Notasi Z=A’B’+AB Z=A + B 74LS266 A Z B A B Z 0 0 1 0 1 0 1 0 0 1 1 1 9 Rangkaian Aritmatika Dengan menggabungkan AND, OR, NOT menurut cara yang sesuai, kita dapat membangun rangkaian yang melakukan penambahan dan pengurangan. Bekerja secara elektroniskerja sangat cepatbeberapa mikrodetik. 10 Rangkaian Aritmatika Tujuan Bab Ini : 1. Menyusun tabel kebenaran gerbang OR-ekslusif, penambah paro dan penambah penuh. 2. Menjelaskan bagaimana bilangan2 biner dapat ditambahkan dalam sebuah penambah biner jajar. 11 Rangkaian Aritmatika Dasar penambah gerbang XOR dan XNOR Z=AB’+A’B Keluaran terjadi 1 bila A atau B adalah 1, namun tidak kedua-duanya (mempunyai keluaran 1 hanya bila masukannya berbeda, keluaran 0 jika masukan2nya sama) 12 Rangkaian Aritmatika 74LS04 A A B 74LS08 74LS86 74LS32 Z Z 74LS08 74LS04 B Rangkaian setara XOR dapat digambarkan dengan 2 buah NOT, 2 buah AND dan 1 buah OR 13 Penambahan Mod-2 A B 74LS86 Z A B Z 0 0 0 0 1 1 1 0 1 1 1 0 14 Penambahan Mod-2 A B 74LS86 Z A B Z 0 0 0 0 1 1 1 0 1 1 1 0 •Gerbang EXOR atau XOR memberikan kepada kita sebuah fungsi baru untuk dipergunakan. Kita akan menggunakan lambang (+) untuk menyatakan fungsi ini. Z = A + B 15 Gerbang XNOR EXNOR (exclusive not OR) Notasi Z=A’B’+AB Z=A + B A B A 74LS266 Z B 74LS86 74LS04 Z Gerbang XOR diikuti sebuah inverter 16 Gerbang XNOR Gambar disamping menunjukkan sebuah pemeriksa paritas bagi bilangan 4 bit. Z=0 untuk paritas genap Z=1 untuk paritas ganjil D C B A 74LS86 74LS86 Z 74LS86 17 Pengecek Paritas 74LS86 D C B A 1 1 1 0 D C B A 1 0 0 1 74LS86 74LS86 74LS86 0genap Z 74LS86 Z 74LS86 Gambar disamping menunjukkan sebuah pemeriksa paritas bagi bilangan 4 bit. Z=0 untuk paritas genap Z=1 untuk paritas ganjil 1ganjil 18 Konverter Biner Gray Z3 Z4 Z5 Z6 74LS86 Z2 74LS86 Z1 74LS86 0 F 1 E C 74LS86 74LS86 1 D 0 B 0 A 1 1 1 0 1 0 1 19 74LS86 D2 C2 B2 A2 D1 74LS86 74LS86 74LS21 Z 74LS86 C1 B1 A1 Pembanding Dua Bilangan Biner 4 Bit 20 F E D C B A Inverter Terkendali (controlled) invert INV (‘0’) = 110001 Z6 Z4 Z3 Z2 ABCDEF=110001 74LS86 74LS86 74LS86 Z5 74LS86 74LS86 Z1 74LS86 INV (‘1’) = 001110 (one’s complement) 21 Penambah Paro (Half Adder) • Penambah Paro menambahkan 2 angka biner pada suatu saat. 74LS08 A Bawaan = AB B 74LS86 Jumlah = A + B Keluaran gerbang XOR merupakan jumlah dan keluaran gerbang AND merupakan bawaan (carry) 22 Penambah Paro (Half Adder) A=0, B=0 Jumlah = A + B = 0 + 0 = 0 Bawaan = AB = 0 . 0 = 0 A=0, B=1 Jumlah = A + B = 0 + 1 = 1 Bawaan = AB = 0 . 1 = 0 74LS08 A Bawaan = AB B 74LS86 Jumlah = A + B A=1, B=0 Jumlah = A + B = 1 + 0 = 1 Bawaan = AB = 1 . 0 = 0 A=1, B=0 Jumlah = A + B = 1 + 1 = 0 Bawaan = AB = 1 . 1 = 1 23 HALF ADDER A B Jumlah Bawaan 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 24 PENAMBAH PENUH (FULL ADDER) Dalam menambahkan 2 bilangan biner, mungkin ada bawaan dari satu kolom ke kolom berikutnya. Contoh: 111 +101 1100 Dalam kolom paling ringan (least significant) 1 + 1 = 0 dengan carry 1 25 PENAMBAH PENUH (FULL ADDER) Dalam kolom berikutnya, harus menambahkan 3 angka akibat adanya carry 1 + 0 + 1 = 0 dengan carry 1 Dalam kolom terakhir harus menambahkan 3 angka akibat adanya carry lagi 1 + 1 + 1 = 1 dengan carry 1 Untuk menambahkan bilangan2 biner secara elektronis, dibutuhkan suatu rangkaian yang dapat menangani 3 angka sekaligus. 26 PENAMBAH PENUH (FULL ADDER) Dengan menghubungkan 2 buah HALF ADDER dan sebuah gerbang OR maka didapat FULL ADDER, dapat menambahkan tiga angka biner pada suatu saat. A B C 74LS32 HA Carry HA Jumlah 27 PENAMBAH PENUH (FULL ADDER) A B C A B C A B C 1 1 0 1 1 1 0 1 0 HA HA HA Carry=1 0 HA Carry=1 0 HA Carry=0 1 HA 74LS32 Carry=1 Carry=0 0 Jumlah= 0 74LS32 Carry=1 Carry=0 1 Jumlah= 1 74LS32 Carry=0 1 Carry=0 Jumlah= 1 28 PENAMBAH PENUH (FULL ADDER) A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 JUMLAH 0 1 1 0 1 0 0 1 CARRY 0 0 0 1 0 1 1 1 29 PENGURANG PARO (HALF SUBTRACTOR) Pada pengurangan biner : 0 – 0 = 0 borrow 0 A B Selisih 0 – 1 = 1 borrow 1 0 0 0 0 0 1 1 1 1 0 1 0 1 1 0 0 1 – 0 = 1 borrow 0 1 – 1 = 0 borrow 0 Borrow 30 PENGURANG PARO (HALF SUBTRACTOR) Keluaran selisih adalah 0 jika masukan A dan B sama, 1 jika berbeda XOR gate Keluaran pinjaman (borrow) bernilai 1 jika A=0 dan B=1 mengANDkan A dan B 74LS86 A Selisih = A + B B 74LS08 74LS04 Borrow = AB 31 PENGURANG PENUH (FULL SUBTRACTOR) Pengurang paro hanya menangani 2 bit biner pada suatu saat dan hanya dapat digunakan pada kolom paling ringan (least significant). Untuk menangani kolom yang lebih tinggi digunakan pengurang penuh menggunakan 2 buah pengurang paro dan sebuah OR. A B Input Borrow HS 74LS32 Borrow HS Borrow Borrow Selisih 32