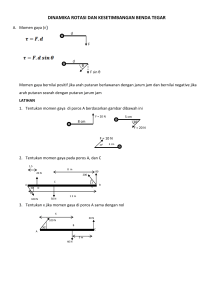
KESEIMBANGAN & DINAMIKA ROTASI Nikmah MAN Kota Palangka Raya Kompetensi Dasar 3.1 Menerapkan konsep torsi, momen inersia, titik berat, dan momentum sudut pada benda tegar (statis dan dinamis) dalam kehidupan sehari-hari 4.1 Membuat karya yang menerapkan konsep titik berat dan keseimbangan benda tegar Kegiatan Pembelajaran • Mengamati demonstrasi mendorong benda dengan posisi gaya yang berbedabeda untuk mendefinisikan momen gaya. • Mendiskusikan penerapan keseimbangan benda titik, benda tegar dengan menggunakan resultan gaya dan momen gaya, penerapan konsep momen inersia, dinamika rotasi, dan penerapan hukum kekekalan momentum pada gerak rotasi. • Mengolah data hasil percobaan ke dalam grafik, menentukan persamaan grafik, menginterpretasi data dan grafik untuk menentukan karakteristik keseimbangan benda tegar • Mempresentasikan hasil percobaan tentang titik berat Materi • • • • • Momen gaya Momen inersia Keseimbangan benda tegar Titik berat Hukum kekekalan momentum sudut pada gerak rotasi A. Torsi atau Momen Gaya • besarnya momen gaya adalah: = F x d = F x d sin θ • Jika 2 gaya atau lebih yang bekerja terhadap suatu proses dirumuskan: tot = 1 + 2 + … + n Contoh soal Momen Gaya (Torsi) 1. UN 2012/2013, Paket 56, Nomor 8 UN 2012/2013, Paket 55, Nomor 8 2. UN 2012/2013, Paket 58, Nomor 8 BSE , Setya Nurachmandani, 171 BSE , Bambang Hatyadi, 120 Kopel • Kopel adalah pasangan dua buah gaya yang sama besar, sejajar dan berlawanan arah. Kopel penyebab sebuah benda berotasi. • Momen kopel merupakan hasil kali vektor antara vektor gaya dan vektor lengan gaya. 3. B. Momen Inersia • Momen inersia partikel Contoh momen inersia • BSE bambang Haryadi, 123 • Soal UN 2012/2013, Paket 60, No : 7 • Soal UN 2012/2013, Paket 56, Nomor 7 A B C • Buku Erlangga, Hal 221, No. 3 D • BSE, Bambang Haryadi, 123 • Perhatikan gambar di bawah ini ! Empat titik materi yang massanya masingmasing 2 gram terletak pada bidang Cartesius. Bila sistem partikel ini diputar terhadap sumbu putar sumbu y, maka hitunglah momen inersianya ! 5. • Momen Inersia benda tegar Contoh momen inersia benda tegar 1. Bola pejal (M = 5 kg) berjari-jari 10 cm berputar pada sumbu yang melalui pusat massanya. Momen inersianya sebesar ... Kg.m2 A. 10-2 C. 3 x 10-2 E. 5 x 10-2 B. 2 x 10-2 D. 4 x 10-2 2. Sebatang kayu panjangnya 100 cm dan bermassa 800 g. Tentukan momen inersia batang kayu itu, jika batang kayu tersebut berputar dengan sumbu putarnya : a. Di tengah-tengah b. di ujung • Contoh : 3. Momen inersia bola pejal terhadap garis singgungnya (gunakan teorema sumbu sejajar) seperti pada gambar berikut adalah .... A. 7/5 MR2 B. 5/2 MR2 C. 3/2 MR2 D. 5/7 MR2 E. 3/2 MR2 4.Momen inersia silinder pejal terhadap garis singgungnya (gunakan teorema sumbu sejajar) seperti pada gambar berikut adalah .... A. 7/5 MR2 B. 5/2 MR2 C. 3/2 MR2 D. 5/7 MR2 E. 2/3 MR2 5. UN Fisika 2008 P04 No. 10 Batang AB homogen panjangnya 6 m dengan massa 4 kg diputar melalui sumbu putar yang terletak 2 m dari ujung A tegak lurus terhadap AB. Momen inersia batang AB adalah .... kgm2 A. 16 B. 12 1 I ml 2 md 2 12 C. 10 D. 7 1 I 4.6 2 4.12 12 E. 4 I 12 4 16 Contoh Soal hubungan momen gaya dan percepatan sudut 1. Sebuah bola pejal yang berdiameter 10 cm diputar terhadap sumbunya, jika bola pejal memiliki percepatan sudut 30 rad/s2 dan massa 4 kg, maka momen gaya yang bekerja pada bola pejal tersebut ialah ... Nm A. 2,40 C. 1,20 E. 0,12 B. 1,50 D. 0,15 2. Sebuah silinder pejal yang berdiameter 10 cm diputar terhadap sumbunya, jika silinder memiliki percepatan sudut 30 rad/s2 dan massa 4 kg, maka momen gaya yang bekerja pada silinder tersebut ialah ... Nm A. 0,15 C. 1,50 E. 15,0 B. 0,30 D. 3,00 3. UN Fisika 2010 P04 No. 7 Sebuah katrol dari benda pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol dengan tali dan gesekan disumbu putarnya diabaikan. Jika momen inersia katrol I = β dan tali ditarik dengan gaya tetap F, maka hubungan yang tetap untuk menyatakan percepatan tangensial katrol adalah.... A. α = F.R. β B. α = F.R. β2 C. α = F.(R. β)−1 D. α = F.R. (β)−1 E. α = (F.R) −1. β 4. UN Fisika 2012 A86 No. 7 Sebuah katrol dari benda pejal dengan tali dililitkan pada sisi luarnya ditampilkan seperti gambar. Gesekan katrol diabaikan. Jika momen inersia katrol I = β dan tali ditarik dengan gaya tetap F, maka nilai F setara dengan.... A. F = α . β . R B. F = α . β2 . R C. F = α . (β .R)−1 D. F = α . β . (R)−1 E. F = R . (α . β)−1 Hukum Kekekalan Momentum Sudut • Momentum sudut didefinisikan sebagai perkalian antara momen inersia dan kecepatan sudut. Secara matematis, ditulis sebagai berikut L = I. ω • dengan: I = momen inersia (kgm2), ω = kecepatan sudut (rad/s), L = momentum sudut (kgm2/s). • Momentum sudut merupakan besaran vektor karena memiliki besar dan arah. Arah momentum sudut dapat ditentukan dengan aturan tangan kanan, seperti yang ditunjukkan pada Gambar • L = kmrv = 2/3 . 0,3. 0,2. 5 = 0,2 Contoh Hukum Kekekalan Momentum Sudut 1. Sebuah piringan silinder pejal homogen mulamula berputar pada porosnya dengan kecepatan sudut 9 rad/s. Bidang piringan sejajar bidang horizontal. Massa dan jari-jari piringan 0,6 kg dan 0,2 m. Bila di atas piringan diletakkan cincin yang mempunyai massa dan jari-jarinya 0,6 kg dan 0,1 m, pusat cincin tepat di atas pusat piringan, maka tentukan kecepatan sudut saat piringan dan cincin bersama-sama berputar. Perubahan Momentum sudut • L = I. = . t 2. Pada sebuah benda bekerja gaya selama 0,25 s, sehingga menghasilkan torsi sebesar 2,5 x 10-2 Nm. Torsi tersebut mengakibatkan perubahan momentum angular benda sebesar ... kgm2 A. 2,5 x 10-2 C. 10 x 10-2 E. 6,25 x 10-3 B. 10 x 10-4 D. 6,25 x 10-2 Pemecahan Masalah Dinamika Rotasi dengan Hukum Kekekalan Energi Misalkan suatu partikel bermassa m bergerak melingkar dengan kecepatan sudut ω, dan jarijari lintasan r. Besar energi kinetik partikel: Dan memiliki kecepatan linear yang besarnya v = ω r EK = EK = EK = Dimana momen inersia adalah EK = Sehingga energi kinetik rotasi benda adalah I = momen inersia (kg.m2) ω = kecepatan sudut (rad/s) Ek rot = energi kinetik rotasi (J) Benda menggelinding • Benda yang menggelinding umumnya berbentuk: 1. Bola pejal (I = 2/5 mR2) 2. Bola tipis berongga (I = 2/3 mR2) 3. Silinder pejal (I = ½ mR2) 4. Silinder tipis berongg (I = mR2) 5. Silinder berongga ( ½ m (R12 + R22) v • Jika dituliskan I k .m.R dan R Ektot = ½ mv2 + ½ Iω2 2 Ektot Ektot 1 2 1 2 mv 2 mv 2 1 2 1 2 v k .m.R R 2 k .m.v 2 2 Ektot 1 2 mv 2 1 k Contoh Ek bidang datar 1. Bola pejal terbuat dari besi menggelinding pada lantai datar dengan laju 15 m/s. Massa bola 2 kg dan berdiameter 40 cm. Energi kinetik total bola adalah ...J A. 90 B. 225 C. 315 D. 400 E. 525 2. Sebuah silinder pejal bertranslasi dan berotasi dengan kecepatan linier dan kecepatan sudut masing-masing v dan ω. Energi kinetik total silinder pejal tersebut adalah .... A. ½ mv2 C. 7/10 mv2 E. 10/9 mv2 B. ¾ mv2 D. 5/2 mv2 Contoh Ek pada bidang miring 1. Sebuah silinder pejal dengan massa 4 kg dan radius 6 cm menggelinding tanpa slip menuruni jalur dengan laju 2 m/s. Energi kinetik totalnya adalah ... joule A. 4 C. 12 E. 20 B. 8 D. 16 2. Sebuah bola pejal dengan massa 5 kg dan radius 6 cm menggelinding tanpa slip menuruni jalur dengan laju 2 m/s. Energi kinetik totalnya adalah ... joule A. 28 C. 14 E. 6 B. 12 D. 7 Hukum kekekalan energi untuk benda menggelinding pada bidang miring Contoh kecepatan benda menggelinding pada bidang miring 1. Sebuah silinder pejal menggelinding pada bidang miring 30o terhadap bidang datar dengan panjang lintasan 5,4 m. Besar kecepatan silinder saat mencapai dasar bidang miring adalah ... m/s A. 5 B. 6 C. 7 D. 8 E. 9 2. Bola pejal bermassa 10 kg mula-mula diam kemudian dilepaskan dari ujung sebuah bidang miring 30o terhadap bidang datar dengan panjang lintasan 56 m. Jari-jari bola adalah 1 meter. Maka kecepatan bola saat tiba di ujung bawah bidang miring ... m/s A. 40 B. 28 C. 20√2 D. 20 E. 2√7 3.Bola pejal bermassa 2 kg menggelinding pada bidang miring. Di titik A kecepatan bola sebesar 2 m/s. Jika hA =dan hB berturut-turut 3 m dan 1,5 m. Tentukan kecepatan bola di B ! • (g = 10 m/s2) A vB 25,4 B hA hB 30o Percepatan benda menggelinding bidang datar • Dinamika gerak lurus : F – fgesek = m.a • Dinamika rotasi a τ = I. α R f gesek F a f gesek .R k .m.R . R f gesek k .m.a F kma m.a F m.a kma F a m1 k 2 Contoh Percepatan benda menggelinding 1. Sebuah silinder pejal massa 2 kg (I = ½ MR2) berada pada lantai kasar diberi gaya 30 N pada pusat massanya sehingga silinder bergerak. Percepatan linier silinder adalah ... m/s2 A. 9 B. 10 C. 12 D. 15 E. 30 2. Sebuah bola pejal massa 2 kg (I = 2/5 MR2) berada pada lantai kasar diberi gaya 28 N pada pusat massanya sehingga bola bergerak. Percepatan linier bola adalah ... m/s2 A. 9 B. 10 C. 12 D. 15 E. 30 Percepatan benda menggelinding pada bidang miring Contoh percepatan benda mengglinding pada bidang miring 1. Sebuah silinder pejal menggelinding dari puncak bidang miring yang sudut elevasinya 30o. Jika percepatan gravitasi 10 m/s2, maka percepatan translasi pusat massa silinder adalah ... m/s2 A. 2,5 B. 3,0 C. 3,3 D. 3,6 E. 4,0 2. Sebuah bola pejal menggelinding dari puncak bidang miring yang sudut elevasinya 30o. Jika percepatan gravitasi 10 m/s2, maka percepatan translasi pusat massa bola adalah ... m/s2 A. 2,5 B. 3,0 C. 3,3 D. 3,6 E. 4,0 Aplikasi Hukum II Newton pada Gerak Rotasi a. Gerak Rotasi pada Katrol - KESETIMBANGAN BENDA TEGAR Contoh Soal Keseimbangan Contoh keseimbanga rotasi Contoh Soal keseimbangan 1.Batang AB panjangnya 5 meter, beratnya 20 N ditumpu pada titik P, AP = 2 m. Pada titik B diberikan beban 50 N, maka supaya batang AB dalam keseimbangan mendatar di titik A harus diberikan gaya sebesar .... A. 55 N C. 75 N E. 100 N B. 60 N D. 80 N 2.Batang AB massanya 5 kg panjangnya 6 m diberi penompang pada jarak 1 m dari ujung A. Pada ujung B diberikan beban 4 kg, agar batang seimbang, ujung A harus diberikan beban ... kg A. 10 C. 20 E. 30 B. 15 D. 25 Contoh keseimbangan translasi dan rotasi NA A NB D 4m W fs C 3m B Fx = 0 NA – fs = 0 NA = fs = s. NB Fy = 0 NB – w = 0 NB = w = m. g = 12. 10 = 120 N = 0 (pusat torsi pada titik B) A - w = 0 NA dAB. Sin = w. dBD. Sin s..w. 5. 4/5 = w. 2. 3/5 s. 4 = 2. 0,6 s = 0,5. 0,6 = 0,3 TITIK BERAT Contoh soal titik berat 1. UN Fisika 2009 P45 No. 5 Letak titik berat bidang homogen di samping ini terhadap titik O adalah ... A. (2, 2) cm B. (2, 3) cm C. (2, 4) cm D. (3, 2) cm E. (3, 3) cm 2. UN Fisika 2008 P4 No. 9 Benda bidang homogen pada gambar dibawah ini, mempunyai ukuran AB=BC=√13 cm. Koordinat titik beratnya terhadap titik E adalah.... A. (1 ; 1,7) cm B. (1 ; 3,6) cm C. (2 ; 3,8) cm D. (2 ; 6,2) cm E. (3 ; 3,4) cm 3. UN Fisika 2010 P37 No. 9 Perhatikan gambar bidang homogen di bawah ini.Koordinat titik berat benda bidang (simetris) terhadap titik O adalah.... A. (2; 4,0) cm B. (2; 3,6) cm C. (2; 3,2) cm D. (2; 3,0) cm E. (2; 2,8) cm 4.UN Fisika 2011 P12 No. 12 Perhatikan gambar! Letak titik berat bidang tersebut terhadap AB adalah.... A. 5 cm B. 9 cm C. 11 cm D. 12 cm E. 15 cm 5. UN Fisika 2012 A86 No. 8 Perhatikan gambar! Letak titik berat bidang homogen terhadap titik O adalah.... A. (0, 8 5/8) B. (0, 7 5/8) C. (0, 5 6/11) D. (0, 4 6/11) E. (0, 3 5/8) 6.UN Fisika 2009 P04 No. 7 Sebuah bidang homogen ABCDE seperti pada gambar! Letak titik ordinat bidang yang diarsir terhadap sisi AB adalah..... A. 1 4/15 cm B. 3 5/8 cm C. 3 4/13 cm D. 5 3/5 cm E. 5 6/13 cm • Analogi gerak translasi dan rotasi