main

KATA PENGANTAR
Segala puji syukur kehadirat Allah SWT yang telah melimpahkan nikmatNya, sehingga
penulisan buku ajar yang berjudul ”Pengantar Metode Numerik” dapat diselesaikan
dengan baik.
Buku ajar ini disusun untuk memenuhi kebutuhan mahasiswa di dalam mengikuti
mata kuliah Metode Numerik, yang isinya disusun secara sistematis dan dilengkapi dengan contoh-contoh soal beserta penyelesainnya yang bertujuan untuk mempermudah
mahasiswa dalam mempelajari materi-materi kuliah yang telah diberikan.
Pada setiap akhir bagian atau sub-sub diberikan latihan-latian soal yang dimaksudkan untuk memperdalam dan memperluas pemahaman mahasiswa, sehingga hasil
yang dicapai menjadi optimal.
Mudah-mudahan dengan adanya buku ajar ini dapat memberikan manfaat kepada
pembaca, khususnya mahasiswa yang mengambil mata kuliah Metode Numerik, dan
sekaligus dapat memberikan kontribusi terhadap pengembangan kurikulum Jurusan
Matematika, Fakultas Sains dan Teknologi UIN SUSKA Riau.
Penulis menyadari bahwa dalam penulisan buku ajar ini masih terdapat kekurangan. Untuk itu, penulis berharap adanya masukan, saran dan kritik yang membangun
dalam rangka penyempurnaan penulisan buku selanjutnya.
Terakhir, ucapan terima kasih kepada pihak-pihak yang telah memberikan masukan, kritikan dan sarannya, semoga menjadi amal kebaikan di sisi Allah SWT.
Pekanbaru, September 2008
Penulis
i
ii
DAFTAR ISI
KATA PENGANTAR
i
DAFTAR ISI
iii
DAFTAR GAMBAR
vii
DAFTAR TABEL
ix
1 KONSEP DASAR
1
1.1
Pengantar Kalkulus Dasar . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2
Evaluasi Polinomial
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.3
Representasi Bilangan Komputer . . . . . . . . . . . . . . . . . . . . . .
14
2 ANALISIS GALAT
1
19
2.1
Definisi dan Pengertian . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
2.2
Sumber Galat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
2.3
Sumber Galat Numerik . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
2.4
Orde Hampiran . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
2.5
Perambatan Galat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3 PENYELESAIAN SISTEM LINEAR
39
3.1
konsep Dasar Sistem Persamaan Linear . . . . . . . . . . . . . . . . . .
39
3.2
Elemninasi Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
3.3
Faktorisasi Matriks LU
. . . . . . . . . . . . . . . . . . . . . . . . . . .
48
3.4
Metode Iterasi untuk Sistem Linear . . . . . . . . . . . . . . . . . . . . .
53
4 AKAR-AKAR PERSAMAAN NONLINEAR
iii
59
4.1
Metode Bagidua . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
4.2
Metode Newton-Raphson . . . . . . . . . . . . . . . . . . . . . . . . . .
67
4.3
Metode Secant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
5 INTERPOLASI
83
5.1
Pengantar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83
5.2
Interpolasi Polinom Lagrange . . . . . . . . . . . . . . . . . . . . . . . .
86
5.2.1
Interpolasi Linear . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
5.2.2
Interpolasi Kuadratik . . . . . . . . . . . . . . . . . . . . . . . .
91
5.2.3
Interpolasi Derajat Tinggi . . . . . . . . . . . . . . . . . . . . . .
94
5.3
Selisih Terbagi Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
5.4
Galat Interpolasi Polinom . . . . . . . . . . . . . . . . . . . . . . . . . . 107
5.5
Polinom Newton-Gregory . . . . . . . . . . . . . . . . . . . . . . . . . . 108
5.5.1
5.6
Polinom Newton-Gregory Maju . . . . . . . . . . . . . . . . . . . 108
Interpolasi Splin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
6 INTEGRASI NUMERIK
123
6.1
Pengertian dan Konsep Dasar . . . . . . . . . . . . . . . . . . . . . . . . 123
6.2
Metode Pias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
6.3
6.4
6.2.1
Kaidah Titik Tengah (Midpoint Rule) . . . . . . . . . . . . . . . 125
6.2.2
Kaidah Trapesium(Trapesium Rule) . . . . . . . . . . . . . . . . 126
Metode Newton-Cotes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
6.3.1
Kaidah Trapesium . . . . . . . . . . . . . . . . . . . . . . . . . . 132
6.3.2
Kaedah Simpson 1/3 . . . . . . . . . . . . . . . . . . . . . . . . . 133
6.3.3
Kaedah Simpson 3/8 . . . . . . . . . . . . . . . . . . . . . . . . . 137
6.3.4
Kaedah Boole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
Penggunaan Ekstrapolasi . . . . . . . . . . . . . . . . . . . . . . . . . . 142
6.4.1
Ekstrapolasi Richardson . . . . . . . . . . . . . . . . . . . . . . . 142
6.4.2
Ekstrapolasi Aitken . . . . . . . . . . . . . . . . . . . . . . . . . 145
6.5
Integrasi Numerik Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
6.6
Integral Tak Wajar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
7 PENYELESAIAN PERSAMAAN DIFERENSIAL BIASA SECARA
iv
NUMERIK
7.1
7.2
161
Persamaan Diferensial Orde Satu . . . . . . . . . . . . . . . . . . . . . . 161
7.1.1
Persamaan Dengan Variabel Terpisah . . . . . . . . . . . . . . . 161
7.1.2
Persamaan Homogen . . . . . . . . . . . . . . . . . . . . . . . . . 163
Metode Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
7.2.1
Tafsiran Metode Euler . . . . . . . . . . . . . . . . . . . . . . . . 165
7.2.2
Analisis Galat Metode Euler . . . . . . . . . . . . . . . . . . . . 166
7.3
Metode Heun (Perbaikan Metode Euler) . . . . . . . . . . . . . . . . . . 173
7.4
Metode Taylor Orde Tinggi . . . . . . . . . . . . . . . . . . . . . . . . . 178
7.5
Metode Runge-Kutta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
7.6
Metode Banyak Langkah . . . . . . . . . . . . . . . . . . . . . . . . . . . 188
7.6.1
Metode Adam-Bashford . . . . . . . . . . . . . . . . . . . . . . . 189
7.6.2
Metode Adam-Moulton . . . . . . . . . . . . . . . . . . . . . . . 190
DAFTAR PUSTAKA
195
v
vi
DAFTAR GAMBAR
1.1
Pendekatan polinomial Taylor orde ke-1, 3 dan 5 terhadap fungsi f (x) =
ex disekitar x0 = 0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2
Pendekatan polinomial Taylor orde ke-1, 3 dan 5 terhadap fungsi f (x) =
ex disekitar x0 = 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3
8
Pendekatan polinomial Taylor orde ke-3 dan 5 terhadap fungsi f (x) =
ln(x + 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1
6
Pendekatan polinomial Taylor orde ke-1, 2 dan 3 terhadap fungsi f (x) =
ln(x) di sekitar x0 = 0. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4
5
9
Skematik metode Bagidua pada kurva y = f (x) yang memotong sumbu
x di α. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
61
4.2
Kurva y = f (x) yang mempunyai akar berjumlah ganjil. . . . . . . . . .
64
4.3
Polinom yang mempunyai akar ganda . . . . . . . . . . . . . . . . . . .
65
4.4
Interval [a, b] yang memuat titik singular kurva y = f (x) . . . . . . . . .
65
4.5
Skematik metode Newton-Raphson pada kurva y = f (x) yang memotong
sumbu x di α. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.6
Konvergensi yang terjadi pada metode Newton . . . . . . . . . . . . . .
71
4.7
Skematik metode Secant pada kurva y = f (x) yang memotong sumbu x
di α. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1
79
Interpolasi (garis tebal) dan ekstrapolasi (garis tipis) terhadap titik-titik
yang diberikan. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
5.2
Interpolasi linear y = P1 (x) . . . . . . . . . . . . . . . . . . . . . . . . .
87
5.3
Interpolasi kuadratik y = P2 (x)
. . . . . . . . . . . . . . . . . . . . . .
91
5.4
Interpolasi polinomial kuadratik y = P2 (x) terhadap fungsi f = 1/x . .
95
vii
5.5
Interpolasi kubik y = P3 (x) . . . . . . . . . . . . . . . . . . . . . . . . .
5.6
y = l(x), interpolasi linear sesepenggal . . . . . . . . . . . . . . . . . . . 116
5.7
y = P6 (x), interpolasi linear derajat enam . . . . . . . . . . . . . . . . . 117
5.8
y = q(x), interpolasi kuadratik sesepenggal . . . . . . . . . . . . . . . . 117
6.1
Luasan daerah yang dibatas oleh kurva y = f (x) di dalam interval [a, b]. 123
6.2
Luasan daerah yang dibatas oleh kurva y = f (x) di dalam interval [a, b]
dengan kaidah Titik Tengah dengan satu sub-interval
6.3
97
. . . . . . . . . . 125
Luasan daerah yang dibatas oleh kurva y = f (x) di [a, b] dengan kaidah
Titik Tengah . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
6.4
Luasan daerah yang dibatas oleh kurva y = f (x) pada interval [a, b]
dengan kaidah Trapesium. . . . . . . . . . . . . . . . . . . . . . . . . . . 127
6.5
Luasan daerah yang dibatas oleh kurva y = f (x) pada interval [a, b]
dengan n sub-interval. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
6.6
Pendekatan Polinom P1 (x) terhadap Luasan daerah yang dibatas oleh
kurva y = f (x) di dalam interval [0, h] dengan Kaidah Trapesium . . . . 132
6.7
Pendekatan Polinom P2 (x) terhadap Luasan daerah yang dibatas oleh
kurva y = f (x) di dalam interval [0, h] dengan kaedah Simpson 1/3 . . . 135
6.8
Integral f (x) pada interval [−1, 1] yang didekati dengan kuadratur Gauss 147
6.9
Kurva y = f (x) singular pada sisi kiri x = a. . . . . . . . . . . . . . . . 153
6.10 Tranformasi bentuk fungsi y = f (x) . . . . . . . . . . . . . . . . . . . . 156
7.1
Kurva persamaan
x2
9
+
y2
4
= C dengan C = 1 dan C = 2. . . . . . . . . 162
viii
DAFTAR TABEL
2.1
Nilai-nilai persamaan (2.2) menggunakan enam angka . . . . . . . . . .
24
2.2
Nilai-nilai persamaan (2.5) menggunakan enam angka . . . . . . . . . .
25
2.3
Nilai-nilai persamaan (2.6) menggunakan tiga digit aritmetik . . . . . .
31
3.1
Konvergensi Iterasi jacobi untuk sistem linear (5.4) . . . . . . . . . . . .
55
3.2
Konvergensi Iterasi Gauss-Seidel untuk sistem linear (3.28) . . . . . . .
57
4.1
Hasil hampiran metode bagidua untuk f (x) = ex − 5x2 dengan toleransi
ε = 0, 001 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2
Hasil hampiran metode bagidua untuk f (x) =
x6
63
− x − 1 = 0 dengan
toleransi ε = 0, 001 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
4.3
Perhitungan akar persamaan f (x) = x6 − x − 1 dengan nilai awal x0 = 1, 5 72
4.4
Perhitungan akar persamaan f (x) = ex − 5x2 dengan nilai awal x0 = 1 .
4.5
Perbadingan kecepatan konvergensi Newton-Raphson baku dan modifikasi pada kasus f (x) = x3 − 5x2 + 7x − 3 dengan nilai awal x0 = 0 . .
4.6
81
Hasil perhitungan enam suku pertama polinomial Taylor terhadap fungsi
f (x) = ex disekitar x = 0 . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2
77
Perbadingan kecepatan konvergensi Newton-Raphson baku dan modifikasi pada kasus f (x) = x3 − 5x2 + 7x − 3 dengan nilai awal x0 = 0 . .
5.1
76
Perbadingan kecepatan konvergensi Newton-Raphson baku dan modifikasi pada kasus f (x) = x3 + 4x2 − 10 dengan nilai awal x0 = 1, 5 . . .
4.7
73
84
Hasil perhitungan enam suku pertama polinomial Taylor terhadap fungsi
f (x) = 1/x disekitar x0 = 1 . . . . . . . . . . . . . . . . . . . . . . . . .
ex
85
5.3
Perkiraann nilai-nilai dari fungsi
. . . . . . . . . . . . . . . . . . . . .
90
5.4
Nilai-nilai dari f (x) = ex . . . . . . . . . . . . . . . . . . . . . . . . . . .
97
ix
5.5
Selisih terbagi Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
5.6
Nilai-nilai f (x) = ex . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
5.7
Tabel Selisih Terbagi Newton orde 4 . . . . . . . . . . . . . . . . . . . . 106
5.8
Tabel Selisih Terbagi Newton orde 4 . . . . . . . . . . . . . . . . . . . . 111
5.9
Selisih Terbagi Pusat Newton . . . . . . . . . . . . . . . . . . . . . . . . 112
5.10 Tabel Selisih Terbagi Newton orde 4 . . . . . . . . . . . . . . . . . . . . 113
5.11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
6.1
Nilai-nilai f (xi ) untuk f (x) = ex dengan lebar sub-interval 0, 2 . . . . . 130
6.2
Nilai-nilai dari kaedah Trapesium . . . . . . . . . . . . . . . . . . . . . . 144
6.3
Hasil pendekatan kuadratur Gauss-Legendre untuk n = 2, 3, 4, 5 dan n = 6150
6.4
Nilai hampiran G(x) dengan h = 0, 25 . . . . . . . . . . . . . . . . . . . 155
7.1
Metode Euler dengan h = 0, 1 . . . . . . . . . . . . . . . . . . . . . . . . 169
7.2
Metode Euler dengan h = 0, 05 . . . . . . . . . . . . . . . . . . . . . . . 169
7.3
Metode Euler dengan h = 0, 1 . . . . . . . . . . . . . . . . . . . . . . . . 170
7.4
Metode Euler dengan h = 0, 05 . . . . . . . . . . . . . . . . . . . . . . . 171
7.5
Metode Heun dengan h = 0, 1 untuk solusi y = 2xy . . . . . . . . . . . 176
7.6
Metode Heun dengan h = 0, 05 untuk solusi y = 2xy . . . . . . . . . . . 177
7.7
Metode Heun dengan h = 0, 1 untuk solusi y = (x + y − 1)2 . . . . . . . 177
7.8
Metode Heun dengan h = 0, 05 untuk solusi y = (x + y − 1)2 . . . . . . 178
7.9
Metode Runge-Kutta dengan h = 0, 1 untuk solusi y = 2xy . . . . . . . 186
7.10 Perbandingan metode Euler, Heun dan Runge-Kutta untuk solusi y =
2xy dengan h = 0, 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187
7.11 Perbandingan metode Adam-Bashfor 4 langkah dan Adam-Moulton 3
langkah untuk solusi y = y − t2 + 1 dengan h = 0, 2 . . . . . . . . . . . 192
x
BAB 1
KONSEP DASAR
1.1
Pengantar Kalkulus Dasar
Pengembangan metode numerik tidak terlepas dari peran serta beberapa definisi
dan teorema dalam kalkulus yang berkenaan dengan fungsi-fungsi polinomial f (x). Oleh
karena itu, beberapa defenisi dan teorema akan dibahas kembali sebagai berikut.
Teorema 1.1 Nilai Tengah
Jika f (x) adalah fungsi kontinu pada interval [a, b] dan didefenisikan m = inf f (x)
a≤x≤b
dan M = sup f (x) maka sebarang ξ pada interval [m, M ], sehingga paling sedikit
a≤x≤b
satu titik ζ di dalam interval [a, b] akan dipenuhi f (ξ) = ζ.
Teorema 1.2 Nilai Rata-rata
Jika f (x) adalah fungsi kontinu pada interval [a, b] dan terdeferensialkan pada interval
(a.b), maka paling sedikit ada satu titik ξ dalam (a, b) yang memenuhi f (b) − f (a) =
f (ξ)(b − a).
Teorema 1.3 Integral Nilai Rata-rata
Jika w(x) adalah fungsi tak negatif dan terintegralkan pada interval [a, b] dan misalkan
f (x) kontinu pada [a, b], maka
b
b
w(x)f (x)dx = f (ξ)
a
untuk semua ξ ∈ [a, b]
w(x)dx
a
.
2
Bab 1 Konsep Dasar
Pada persolaan matematika, terdapat beberapa fungsi f (x) yang bentuknya
komplek sehingga tidak dapat ditentukan nilai eksaknya dengan cara yang lebih sederhana. Misalnya f (x) = ex , dan kita akan mengalami kesulitan untuk menghitung nilai
f (x) tanpa bantuan komputer atau kalkulator. Untuk itu, fungsi f (x) akan didekati
dengan polinom hampiran, karena polinom adalah fungsi yang paling mudah dipahami
kelakuannya.
Misalkan f kontinu dan terdeferensiabel untuk f , f , f (3) , · · · pada selang [a, b].
Jika diberikan x0 ∈ [a, b], maka untuk nilai-nilai x di sekitar x0 , maka f (x) dapat
diperluas,
(x − x0 ) (x − x0 ) (x − x0 ) f (x0 ) +
f (x0 ) +
f (x0 ) + · · ·
1!
2!
3!
(x − x0 ) (n)
f (x0 ) + · · ·
(1.1)
+
n!
f (x) = f (x0 ) +
Oleh karena deret Taylor tak terhingga banyaknya, maka untuk hampiran orde
ke-n, disebut deret Taylor terpotong yang ditulis,
(x − x0 ) (x − x0 ) (x − x0 ) f (x0 ) +
f (x0 ) +
f (x0 ) + · · ·
1!
2!
3!
(x − x0 ) n
(1.2)
f (x0 ) + R(n) (x)
+
n!
f (x) = f (x0 ) +
dengan
Rn (x) =
(x − x0 )n+1 (n+1)
f
(ξ(x)), x0 < ξ < x
(n + 1)!
disebut galat atau sisa orde ke-n. Dengan demikian deret Taylor yang dipotong sampai
suku orde ke-n dapat ditulis kembali dalam bentuk,
f (x) = Pn (x) + Rn (x)
dengan,
Pn (x) =
n
(x − x0 )k (k)
f (x0 )
k=1
k!
Dalam hal ini, Pn (x) disebut Polinomial Taylor ke-n untuk f di sekitar x0 dan
Rn (x) disebut suku sisa (galat pemotongan) yang berhubugan dengan Pn (x). Deret
tak hingga Taylor diperoleh dengan mengambil limit Pn (x) untuk n → ∞ yang disebut
deret Taylor untuk f di sekitar x0 . Untuk kasus khusus, jika fungsi f (x) diperluas di
1.1 Pengantar Kalkulus Dasar
3
sekitar x0 = 0, maka deretnya disebut deret MacLaurin, sehingga persamaan (1.2)
menjadi,
x
x
x
x f (0) + f (0) + f (0) + · · · + f (n) (0)
1!
2!
3!
n!
+Rn (x)
f (x) = f (0) +
(1.3)
Teorema 1.4 Teorema Taylor
Jika f (x) mempunyai n + 1 turunan kontinu pada interval [a, b] untuk beberapa n ≥ 0
dan bila x, x0 ∈ [a, b], maka
f (x) ≈ Pn (x) + Rn+1 (x)
(1.4)
dengan
Pn (x) = f (x0 ) + (x − x0 )f (x0 ) +
(x − x0 )2 (x − x0 )n (n)
f (x0 ) + · · · +
f (x0 )
2!
n!
(1.5)
dan
Rn+1 (x) =
=
1 x
(x − t)n f (n+1) (t)dt
n x0
(x − x0 )n+1 (n+1)
f
(ξ(x))
(n + 1)!
(1.6)
Deret Taylor tersebut menjadi konsep dasar metode numerik. Beberapa pendekatan numerik dihasilkan dari pemenggalan deret Taylor.
Contoh 1.1
Dekati fungsi
f (x) = ex
dengan polinomial orde ke-1, 3 dan 5 disekitar x0 = 0.
Penyelesaian:
f (x) = ex , f (x) = ex , f (x) = ex , · · · , f (5) (x) = ex . Berdasarkan persamaan (1.2),
4
Bab 1 Konsep Dasar
pendekatan deret Taylor orde ke-1,
(x − 0) (x − 0)2 ζ
+
e
1!
2!
1 2 ξ
x e
= 1 +
x
+
2
ex = e0 +
P1
R1
dan pendekatan polinomial Taylornya adalah,
ex ≈ 1 + x
Pendekatan deret Taylor orde ke-3,
(x − 0) 0 (x − 0)2 0 (x − 0)3 0 (x − 0)4 ζ
e +
e +
e +
e
1!
2!
3!
4!
1
1
x4
= 1 + x + x2 + x3 + eζ
2
6 24 ex = e0 +
P3
R3
dan pendekatan polinomial Taylornya adalah,
1
ex ≈ 1 + x + x2
2
Pendekatan polinomial Taylor orde ke-5,
(x − 0) 0 (x − 0)2 0 (x − 0)3 0 (x − 0)4 0
e +
e +
e +
e
1!
2!
3!
4!
(x − 0)5 0 (x − 0)6 ζ
e +
e
+
5!
6!
1
1
1
1 5
x5 ζ
x +
e
= 1 + x + x2 + x3 + x4 +
2
6 24
120 720
ex = e0 +
P5
R5
dan pendekatan polinomialnya adalah,
1
1
1
1 5
x
ex ≈ 1 + x + x2 + x3 + x4 +
2
6
24
120
Gambar 1.1 menunjukkan secara geometri daripada pendekatan polinomial Taylor orde ke-1, 3, dan 5 terhadap fungsi f (x) = ex .
1.1 Pengantar Kalkulus Dasar
5
Y
f (x) = ex
12
9
P5 x
6
P3 x
P1 x
3
X
-2
-1
0
1
2
Gambar 1.1 Pendekatan polinomial Taylor orde ke-1, 3 dan 5 terhadap fungsi
f (x) = ex disekitar x0 = 0.
Contoh 1.2
Dekati fungsi
f (x) = ex
dengan polinomial orde ke-1, 2 dan 5 disekitar x0 = 1.
Penyelesaian:
f (x) = ex , f (x) = ex , f (x) = ex , · · · , f (4) (x) = ex . Berdasarkan persamaan (1.2),
pendekatan polinomial Taylor orde ke-1 disekitar x0 = 1
(x − 1) f (x0 )
1!
= e1 + (x − 1)e1
P1 (x) = f (x0 ) +
= xe
Pendekatan polinomial Taylor orde ke-2
(x − 1) (x − 1)2 f (x0 ) +
f (x0 )
1!
2!
= e + (x − 1)e + (x − 1)2 e
P2 (x) = f (x0 ) +
= e(1 + x − 1 + x2 − 2x − 1)
= e(−1 − x + x2 )
Pendekatan polinomial Taylor orde ke-5,
P5 (x) = f (x0 ) +
(x − x0 ) (x − x0 )2 (x − x0 )5 (5)
f (x0 ) +
f (x0 ) + · · · +
f (x0 )
1!
2!
5!
6
Bab 1 Konsep Dasar
(x − 1) 1 (x − 1)2 1 (x − 1)3 1 (x − 1)4 1 (x − 1)5 1
e +
e +
e +
e +
e
1!
2!
3!
4!
5!
1
1
= e 1 + (x − 1) + (x2 − 2x + 1) + (x3 − 3x2 + 3x − 1)
2
6
= e1 +
1
1
(x5 − 5x4 + 10x3 − 10x2 + 5x1 )
+ (x4 + 4x3 + 6x2 + 4x + 1) +
24
120
17
1
5
1 5
4
+ x + x2 + x3 +
x
= e
30 24
6
12
120
Gambar 1.2 menunjukkan secara geometri daripada pendekatan polinomial Taylor orde
ke1, 3, dan 5 terhadap fungsi f (x) = ex di sekitar x0 = 1.
P5 x
Y
f (x) = ex
12
P2 x
9
P1 x
6
3
X
-2
-1
0
1
2
Gambar 1.2 Pendekatan polinomial Taylor orde ke-1, 3 dan 5 terhadap fungsi
f (x) = ex disekitar x0 = 1.
Contoh 1.3
Diketahui fungsi f (x) = ln(x), tentukan polinomial Taylor orde ke-1 dan 2 untuk
mendekati fungsi tersebut pada titik x0 = 1 dan kemudian hitung pada x = 2.
Penyelesaian:
Dari soal diketahui f (x) = ln(x), maka f (x) = x−1 , f (x) = −x−2 dan f (x) = 2x−3 .
Ole karena itu, polinomial Taylor orde ke-1,
ln(x) ≈ P1 (x) = ln(1) + (x − 1)(1) = 0 + (x − 1)
1.1 Pengantar Kalkulus Dasar
7
= x−1
dan polinomial Taylor orde ke-3, adalah
(x − 1)2
(x − 1)2
(−1) +
(2)
2!
3!
1
1
= (x − 1) − (x − 1)2 + (x − 1)3
2
3
1 3 3 2
11
=
x − x + 3x −
3
2
6
ln(x) ≈ P3 (x) = ln(1) + (x − 1)(1) +
Dari uraian di atas, maka nilai ln(2) dapat ditentukan dengan menggunakan pendekatan
polinomial Taylor untuk orde ke-1 di atas,
ln(2) ≈ P1 (2) = (2 − 1) = 1
dan
1
1
ln(2) ≈ P3 (2) = (2 − 1) − (2 − 1)2 + (2 − 1)3
2
3
1
1
= 1 − (1) + (1)
2
3
2
=
3
Gambar 1.3 menunjukkan secara geometri daripada pendekatan polinomial Taylor orde
ke-1, 2, dan 3 terhadap fungsi f (x) = ln(x) di sekitar x0 = 0.
Contoh 1.4
Dekati fungsi
f (x) = ln(x + 1)
dengan polinomial orde-3 dan 5 di sekitar x0 = 0.
Penyelesaian:
Dari soal,
f (x) = ln(x + 1), maka,
f (x) = (x + 1)−1 , f (x) = −(x + 1)−2 , f (x) = 2(x + 1)−3 , · · · , f (5) (x) =
24(x + 1)−5 .
8
Bab 1 Konsep Dasar
Y
8
P3 (x)
6
-1
4
P1 (x)
2
f (x) = ln(x + 1)
0
X
0
1
2
3
4
5
-2
-4
P2 (x)
Gambar 1.3 Pendekatan polinomial Taylor orde ke-1, 2 dan 3 terhadap fungsi
f (x) = ln(x) di sekitar x0 = 0.
Dengan menggunakan rumusan polinomial Taylor, diperoleh,
(x − 0)
(x − 0)2
(0 + 1) +
(−(0 + 1)−2 )
1!
2!
(x − 0)3
(x − 0)3
+
(2(0 + 1)−3 ) +
(24(ξ + 1)−6 )
3!
3!
1
1
1
= 1 + x(1) + x(−1) + x3 (2) + x4 (6(ξ + 1)−4 )
2
6
24
1 2 1 3 1 4
= 1 + x − x + x − x (ξ + 1)−4
2
3 4
ln(x + 1) = ln 0 + 1 +
P3
R3
sehingga pendekatan P3 (x) terhadap f (x) diberikan oleh,
1
1
ln(x + 1) ≈ P3 (x) = 1 + x − x2 + x3
2
3
Deret Taylor orde ke-5 untuk x0 = 0 adalah
(x − 0)
(x − 0)2
(0 + 1) +
(−(0 + 1)−2 ) + · · ·
1!
2!
(x − 0)5
(x − 0)6
+
(24(0 + 1)−5 ) +
(−120(ξ + 1)−6 )
5!
6!
x2 x3 x4 x5 x6
+
−
+
= 1+x−
− (ξ + 1)−6
2
3
4
5
6 ln(x + 1) = ln 0 + 1 +
P5
R5
sehingga pendekatan P5 (x) terhadap f (x) diberikan oleh,
n(x + 1) ≈ P5 (x) = 1 + x −
x2 x3 x4 x5
+
−
+
2
3
4
5
1.1 Pengantar Kalkulus Dasar
9
Gambar 1.4 menunjukkan secara geometri daripada pendekatan polinomial Taylor orde
ke1, 3, dan 5 terhadap fungsi f (x) = ex .
Galat Deret Taylor
Y
P5 (x)
8
4
P3 (x)
f (x) = ln(x + 1)
-1
0
X
0
1
2
-4
Gambar 1.4 Pendekatan polinomial Taylor orde ke-3 dan 5 terhadap fungsi
f (x) = ln(x + 1).
Teorema 1.5 (Teorema Taylor)
Asumsikan bahwa f (x) mempunyai n + 1 derivatif pada interval [a, b]. Misalkan
terdapat x0 ∈ [a, b], untuk polinomial Taylor Pn (x) pada persamaan (1.2), maka
Rn (x) = f (x) − Pn (x)
yang melambangkan sisa pendekatan polinomial Pn (x) terhadap f (x), ditulis
Rn (x) =
(x − x0 )n+1 (n+1)
f
(ξ)
(n + 1)!
dengan ξ adalah titik tak diketahui diantara x0 dan x
Misalkan f (x) = ex dan x0 = 0, maka polinomial Taylornya adalah
Pn (x) = 1 + x +
n
1 2
1
1 j
x + · · · + xn =
x
2!
n!
j!
j=0
(1.7)
10
Bab 1 Konsep Dasar
dan dari teorema di atas, galat pendekatan yang diberikan adalah
ex − Pn (x) =
xn+1 ξ
e ,
(n + 1)!
n≥0
(1.8)
dengan ζ di antara 0 dan x. Pada kasus tertentu, ambil x = 1, maka dari persamaan
(5.17),
e ≈ Pn (1) = 1 + 1 +
1
1
1
+ + ··· +
2! 3!
n!
dan dari persamaan (1.8) diperoleh,
e − Pn (1) = Rn (1) =
eξ
,
(n + 1)!
0<ζ<1
Dari defenisi yang diberikan pada kalkulus, maka dengan mudah diperoleh batas, e < 3.
Hal ini mengakibatkan batas Rn (1) adalah
3
e
1
≤ Rn (1) ≤
<
(n + 1)!
(n + 1)!
(n + 1)!
Dengan menggunakan ketaksamaan diperoleh e0 ≤ eζ < e1 . Jika dimisalkan galat yang
ditimbulkan oleh pendekatan Pn (1) terhadap fungsi e adalah
Rn (1) ≤ 10−9 , maka
batas orde minimalnya agar tingkat kesalahan memenuhi persamaan di atas, maka
3
≤ 10−9
(n + 1)!
3
≤ 10−9
1 · 2 · 3 · · · (n − 2)(n − 1)(n)(n + 1)
n ≥ 12
Jadi P12 (1) adalah cukup akurat untuk pedekatan terhadap e dengan galat 10−9 .
1.1 Pengantar Kalkulus Dasar
11
Latihan
1.1
1. Dengan menggunakan deret Maclaurin, bandingkan nilai-nilai log(x) untuk orde2, 3, dan 4 pada interval
2 3
3, 2
2. Dekati fungsi-fungsi berikut dengan menggunakan deret Taylor linear dan kuadratik.
√
a f (x) =
x, a = 1
b f (x) = sin x, a = π/4
c f (x) = ecos (x) , a = 0
3. Gunakan deret Taylor orde-n di x0 = 0 untuk mendekati fungsi-fungsi berikut.
a. f (x) = 1/(1 − x)
b. f (x) = sin(x)
√
c. f (x) = 1 + x
4. Gunakan deret Taylor orde 3 dan 4 untuk mendekati f (x) = (1/x)(log(1 + x)
5. Gunakan polinomial Taylor untuk menghampiri cos 42◦ di sekitar x0 = π/4 dengan
akurasi 10−6
6. Tentukan polinomial Taylor kedua P2 (x) untuk fungsi ex cos(x) yang diekspan di
sekitar x0 = 0.
a. Gunakan P2 (0, 5) untuk mendekati f (0, 5), dan tentuka batas atas galat
|f (0, 5) − P2 (0, 5)| dengan menggunakan rumus galat polinomial Taylor dan
bandingkan hasilnya dengan nilai sebernarnya.
1
b. Dekati
0
P2 (x)dx
7. Misalkan f (x) = (1 − x)−1 dan x0 = 0. Tentukan polinomial Pn (x) = f (x) yang
diekspand disekitar x0 . Tentukan nilai n untuk Pn (x) mendekati f (x) dengan
galat maksimum 10−6 pada interval [0; 0, 5]
12
Bab 1 Konsep Dasar
8. Misalkan f (x) = ex dan x0 = 0. Tentukan polinomial Pn (x) = f (x) yang diekspad
disekitar x0 . Tentukan nilai n untuk Pn (x) mendekati f (x) dengan galat maksimum 10−6 pada interval [0; 0, 5]
2
9. Tentukan polinomial Taylor ke-empat untuk mendekati fungsi f (x) = xex yang
diekspad disekitar x0 = 0.
a. Tentukan batas maksimum |f (x) − P4 (x)| pada interval [0; 0, 4]
0,4
b. Dekati
0
0,4
f (x)dx dengan menggunakan
0
P4 (x)dx
10. Polinomial P2 (x) = 1 − 12 x2 digunakan untuk mendekati f (x) = cos(x) pada
1 1
interval − , . Tentukan batas galat maksimum tersebut.
2 2
11. Misalkan f (x) = 2x cos(2x) − (x − 2)2 dan x0 = 0.
a. Tentukan polinomial Taylor ke-2, P2 (x), untu menghampiri f (0, 4)
b. Dengan menggunakan P2 (x), tentukan batas atas untuk galat |f (0, 4)−P2 (x)|
c. Tentukan polinomial Taylor ke-5, untuk menghampiri f (0, 4)
d. Gunakan polinomial Taylor P5 (x) untuk menentukan batas atas galat |f (0, 4)−
P5 (x)|
1.2
Evaluasi Polinomial
Mengevaluasi polinomial kadang-kadang muncul pada kasus-kasus tertentu. Sekarang
pertimbangkanm suatu polinomial berikut.
p(x) = 3 − 4x + 5x2 − 6x3 + 7x4 − 8x5
Dari perspektif seorang programer, cara yang paling sederhana adalah dengan mengevaluasi setiap suku secara terpisah. Mengevaluasi dengan cara seperti ini akan banyak
membutuhkan perhitungan. Misalkan suku axk membutuhkan k perkalian, maka jumlah perkalian yang akan dilakukan pada kasus di atas adalah
1 + 2 + 3 + 4 + 5 = 15 perkalian
1.2 Evaluasi Polinomial
13
dalam mengvaluasi polinomial p(x). Cara kedua yang dapat dilakukan adalah dengan
menyederhanakan bentuk pangkat. Cara ini lebih efesien dibandingkan dengan cara
pertama. Jadi bentuk
x3 = x(x2 ),
x4 = x(x3 ),
x5 = x(x4 )
Jadi setiap suku axk membutuhkan dua perkalian untuk k > 1, sehingga evaluasi p(x)
menggunakan
1 + 2 + 2 + 2 + 2 = 9 perkalian
Cara ketiga biasa disebut perkalian bersarang. Bentuk polinom di atas dapat ditulis
kembali dalam bentuk,
p(x) = 3 + x(−4 + x(5 + x(−6 + x(7 − 8x))))
Jumlah perkalian yang dibutuhkan hanya 5, dan ini membuktikan bahwa cara ketiga
lebih menghemat dibandingkan cara kedua.
Perkalian bersarang ini dapat dikembangkan terhadap polinom dengan orde yang
lebih tinggi. Pertimbangkan polinom berorde-n,
p(x) = a0 + a1 x + a2 x2 + a3 x3 + · · · + an xn , a0 = 0
(1.9)
Jika kita menggunakan cara kedua, maka kita akan membutuhkan 2n − 1 perkalian,
sedangkan jika menggunakan perkalian bersarang, maka kita tulis kembali dalam bentuk,
p(x) = a0 + x(a1 + x(a2 + · · · + x(xn−1 + an x) . . .)
(1.10)
Dengan cara ini, kita hanya menggunakan n perkalian dan ini menghemat sampai 50%
lebih dibandingkan dengan metode kedua.
Contoh 1.5
Evaluasi polinomial Taylor p5 (x) untuk log(x) disekitar x0 = 1
Penyelesaian:
Secara umum, bentuk polinomial Taylor orde ke-5 dari log(x) adalah,
1
1
1
1
log(x) = p5 (x) = (x − 1) − (x − 1)2 + (x − 1)3 − (x − 1)4 + (x − 1)5
2
3
4
5
(1.11)
14
Bab 1 Konsep Dasar
Misalkan z = (x − 1), maka
1
1
1
1
p5 (x) = z − z 2 + z 3 − z 4 + z 5
2
3
4
5
1
1
1
1
+z − = z
= z 1+z − +z
2
3
4
5
1.3
Representasi Bilangan Komputer
Perhitungan yang dilakukan oleh kalkulator atau komputer akan sangat berbeda
dengan perhitungan yang dilakukan oleh kita pada materi kalkulus atau aljabar. Kita
√
akan mudah menghitung 2 + 2 = 4, 42 = 16 dan ( 3)2 = 3. Hal ini akan berbeda
√
jika dihitung dengan menggunakan perhitungan komputer. Untuk menghitung ( 3)2 ,
√
komputer akan menghitung terlebih dahulu bentuk 3 selanjutnya mengkuadratkan√
nya. Pada perhitungan komputer, 3 menghasilkan nilai desimal yang tidak terhingga,
sehingga nilai tersebut merupakan nilai pendekatan. Hal ini dapat dipahami karena
√
3 = 1, 7320508 . . ..
Oleh karena keterbatasan desimal pada komputer, maka dalam memberikan nilai pendekatan ini, komputer melakukan pemotongan (chopping) atau pembulatan
(Rounding) sehingga memunculkan kesalahan yang secara umum dikenal dengan nama
kesalahan pemotongan (chopping error) dan kesalahan pemotongan (rounding error).
Untuk mempresentasikan bilangan real, komputer menggunakan sistem bilangan
titik kambang (floating point number) dengan basis bilangan 2 (biner), basis bilangan 8
(octal) dan basis bilangan 16 (heksadecimal), dengan format
x = σ · (d1 d2 · · · dt )β · β e
(1.12)
dengan
a1 = 0 dan 0 ≤ ai ≤ β, a1 disebut titik radik
σ adalah tanda dengan nilai σ = +1 atau σ = −1 dan β adalah basis
e adalah bilangan bulat dengan L ≤ e‘U dimana L, U masing-masing nilai terkecil dan terbesar.
(d1 d2 · · · dt )β adalah mantisa
Penggunaan bilangan dengan basis-basis 2, 8 dan 16 cukup sulit, oleh karena itu bilan-
1.3 Representasi Bilangan Komputer
15
gan mesin dinormalkan ke dalam bentuk bilangan titik kambang desimal yang ditulis
x = ±.d1 d2 · · · dk × 10n ,
1 ≤ d1 ≤ 9,
0 ≤ di ≤ 9,
(1.13)
untuk setiap i = 2, 3, . . . , k Untuk sembarang bilangan real positif y dapat dinormalisasi
ke dalam bentuk,
y = 0, d1 d2 . . . dk dk+1 dk+2 . . . × 10n
Jika kita akan melakukan pemotongan terhadap y dengan pemotongan dk+1 dk+2 . . .,
maka diperoleh,
A = 0, d1 d2 . . . dk . . . × 10n
Cara ini disebut pemotongan bilangan. Pada metode ini, jika nilai dk+1 ≥ 5, kita dapat
menambahkan nilai satu pada dk , dan jika dk+1 ≤ 5 kita menghilangkannya kecuali k
bilangan pertama. Cara ini disebut pembulatan bilangan.
Definisi 1.1 Galat Mutlak dan Relatif
Jika p∗ adalah aproksimasi terhadap p, galat mutlak |p − p∗ | dan galat relatif
dengan p = 0
|p − p∗ |
|p|
Contoh 1.6
Persamaan kuadratik menyatakan bahwa akar-akar persamaan ax2 + bx + c = 0, a = 0
adalah
x1 =
−b +
√
b2 − 4ac
2a
dan x2 =
−b −
√
b2 − 4ac
2a
Selanjutnya, hitunglah x2 + 62, 10x + 1 = 0.
Penyelesaian:
Persamaan di atas mempunyai akar-akar persamaan sejati,
x1 = −0, 01610723
dan x2 = −62, 08390
Pada persamaan ini, nilai b2 sangat besar dibandingkan dengan 4ac, oleh karena itu pembilang pada perhitungan untuk x1 melibatkan operasi penjumlahan dari dua bilangan
16
Bab 1 Konsep Dasar
yang hampir sama nilainya. Misalkan kita akan menghitung x1 dengan menggunakan
empat digit pemotongan,terlebih dahulu kita hitung,
b2 − 4ac =
(62, 10)2 − 4, 000 =
3856 − 4, 000 =
√
3852 = 62, 06
dan
√
b2 − 4ac
2a
−62, 10 + 62, 06
=
2, 000
−0, 04000
= −0, 02000
= =
2, 000
A(x1 ) =
−b +
Jika nilai x1 sejati adalah x1 = −0, 01611, maka galat relatifnya cukup besar,
| − 0, 01611 + 0, 02000|
≈ 2, 4 × 10−1
| − 0, 01611|
Selanjutnya, untuk menentukan x2 , kita akan melibatkan pengurangan dua bilangan
√
yang hampir sama, yaitu −b dan − b2 − 4ac,
√
−b + b2 − 4ac
A(x2 ) =
2a
−62, 10 − 62, 06
=
2, 000
−124, 2
= −62, 10
=
2, 000
Jika nilai sejati x2 = −62, 08, maka galat relatif adalah
| − 62, 08 + 62, 10|
≈ 3, 2 × 10−4
| − 62, 08|
Untuk memperoleh akurasi pendekatan lebih dari empat digit untuk x1 , maka kita akan
mengubah bentuk rumusan akar kuadratik dengan merasionalkan pembilang (bukan
dalam bentuk akar), yaitu:
x1 =
=
=
−b +
√
b2 − 4ac
2a
√
−b − b2 − 4ac
√
−b − b2 − 4ac
b2 − (b2 − 4ac)
√
2a(−b − b2 − 4ac)
−2c
√
b + b2 − 4ac
(1.14)
1.3 Representasi Bilangan Komputer
17
Dengan menggunakan (1.14), maka
A(x1 ) =
−2, 000
−2, 000
=
= −0, 01610
62, 10 + 62, 06
124, 2
dengan galat relatif,
| − 0, 01611 − (−0, 01610)|
≈ 6, 2 × 10−4
| − 0, 01611|
Teknik merasionalkan pembilang juga diterapkan untuk menentukan x2 , yaitu
x2 =
−2c
√
b − b2 − 4ac
(1.15)
Tetapi, bentuk (1.15) memunculkan galat relatif yang besar. Hal ini disebabkan karena
pada penyebut terdapat operasi pengurangan (karena b bernilai positif), sehingga nilai
penyebut menjadi kecil,
A(x2 ) =
degan galat relatif
−2, 000
−2, 000
=
= −50, 000
62, 10 − 62, 06
0, 04000
| − 62, 08 − 50, 000|
≈ 1, 9 × 10−1
| − 62, 08|
18
Bab 1 Konsep Dasar
BAB 2
ANALISIS GALAT
Sebagian besar numerik digunakan untuk menyelesaian persoalan-persoalan yang berkaitan dengan perhitungan komputer. Oleh karena pada sub-bab sebelumnya telah dijelaskan bahwa perhitungan dengan menggunakan komputer memberikan atau memunculkan galat yang disebut galat pemotongan dan galat pembulatan. Selain itu, galat
juga muncul yang disebabkan oleh suatu metode atau kaedah yang memang memberikan
sumber kesalahan.
2.1
Definisi dan Pengertian
Galat dalam pengertian umum disefinisikan,
galat = nilai sejati - nilai pendekatan
sedangkan galat relatif adalah ukuran galat yang berhubungan dengan size nilai sejati
yang ditulis,
galat relatif =
galat
nilai sejati
Misalkan x̂ pendekatan dari nilai sejati x, maka galat ditulis,
ε = x − x̂
Bentuk ungkapan di atas sering juga disebut galat mutlak. Ukuran galat ε yang diperoleh tidak menunjukkan seberapa besar galat jika dibandingan dengan nilai sejati x.
Sebagai contoh, jika seorang memperoleh galat sebesar 1 cm terhadap pengkuruan meja
dan pensil yang masing-masing panjangnya 100 cm dan 10 cm. Galat sebesar 1 cm yang
diperoleh dari pengukuran pensil lebih berarti daripada galat yang diperoleh dari pengukuran meja. Untuk mengatasi intepretasi ini, maka galat dinormalkan terhadap nilai
20
Bab 2 Analisis Galat
sejatinya. Galat yang diperoleh dengan cara seperti ini disebut galat relatif, ditulis
εr =
x − x̂
x
Jika galat ε dinormalkan terhadap nilai hampiran x̂, maka galat ini disebut galat relatif
hampiran, ditulis,
εrh =
x − x̂
x̂
Sebagai ilustrasi, perhatikan contoh berikut.
Contoh 2.1
Misalkan x = 10/3, dan x̂ = 3, 3333
Penyelesaian:
Galat (ε),
10
− 3, 3333
3
1
10.0000 99999
−
=
=
30000
30000
30000
= 0, 00003333 · · ·
ε = x − x̂ =
Galat relatif (εr ),
x − x̂
ε
=
x
x
3
1/30000
=
=
10/3
300000
= 0, 00001
εr =
Galat relatif hampiran (εrh ),
εrh =
=
=
ε
x − x̂
=
x̂
x̂
1/300000
1/30000
=
0, 3333
3333/10000
1
99999
2.1 Definisi dan Pengertian
21
Contoh 2.2
Tentukan galat, galat relatif, dan galat relatif hampiran jika diberikan y = 1.000.000
dan ŷ = 999.996.
Penyelesaian:
Galat,
ε = y − ŷ = 1.000.000 − 999.996
= 4
dan galat relatif,
ε
y − ŷ
=
y
y
4
=
1.000.000
= 0, 000004
εr =
galat relatif hampiran,
εrh =
=
=
ε
y − ŷ
=
ŷ
ŷ
4
999.996
1
24999
Latihan
2.1
1. Hitung galat mutlak dan galat relatif dari hampiran p terhadap p∗ :
a. p = π, p∗ = 22/7
b. p = e, p∗ = 2, 718
c. p = e10 , p∗ = 22000
d. p = 8!, p∗ = 39900
e. p = π, p∗ = 3, 1416
√
f. p = 2, p∗ = 1, 414
g. p = 10π , p∗ = 1400
√
h. p = 9!, p∗ = 18π(9/e)9
2. Tentukan perhitungan secara (i) eksak, (ii) menggunakan tiga digit aritmetika
pemotongan, (iii) tiga digit aritmetik pembulatan, dan (iv) galat relatif dari (ii)
dan (iii).
22
Bab 2 Analisis Galat
4 1
+
5 3 3
3
1
−
+
c.
3 11
20
a.
4 1
·
5 3
3
3
1
d.
−
−
3 11
20
b.
3. Gunakan tiga digit aritmetik pembulatan, pada perhitungan berikut. Dengan
menentukan nilai sejati (minimal lima digit), hitunglah galat relatif dan galat
absolutnya.
2.2
a. 133 + 0, 921
b. 133 − 0, 499
c. (121 − 0, 327) − 119
13/14 − 6/7
e.
2e− 5,4
2
9
g.
9
7
d. (121 − 119) − 0, 327
f. −10π + 6e −
h.
3
62
π − 22/7
1/17
Sumber Galat
Misalkan kita akan menyelesaikan sebuah persoalan matematika yang melibatkan
proses komputerisasi, maka galat biasanya akan muncul pada proses ini, bahkan kadangkadang beberapa jenis galat muncul. Berikut ini beberapa sumber galat yang mungkin
muncul pada penyelesain persoalan matematika.
1. Persamaan matematika digunakan untuk merepresentasikan suatu penomena fisika,
dan proses mengubah dari bentuk penomena fisika ke bentuk rumusan matematika disebut pemodelan matematika. Pemodelan seperti ini memunculkan galat
terhadap persoalan yang akan diselesaikan.
Pertimbangkan persamaan pertumbuhan populasi berikut,
N (t) = N0 ekt
(2.1)
dengan N (t) adalah populasi pada waktu t, N0 adalah populasi awal, dan k adalah
suatu konstanta positif. Untuk beberapa kasus, selama t masih terbatas, maka
model tersebut masih dapat digunakan, namun untuk kasus t → ∞ atau t yang
sangat besar sekali, maka model menjadi overestimate.
2. Pada pengukuran data-data penomena fisika, maka data-data tersebut mengandung galat. Sebagai contoh adalah kecepatan cahaya pada keadaan ruang hampa,
2.2 Sumber Galat
23
yaitu
c = (2, 997925 + ) · 1010 cm/sec,
|| ≤ 0, 000003
Oleh karena data yang digunakan mengadung galat, maka perhitungan-perhitungan
yang melibatkan data-data fisika juga akan memunculkan galat. Numerik tidak
dapat menghilang galat dari data tersebut, bahkan akibat adanya galat pada data
tersebut, dapat menimbulkan pengulangan/akumulasi galat pada proses perhitungan. Numerik hanya dapat meminimalkan galat yang ditimbulkan.
3. Galat yang ditimbulkan oleh mesin itu sendiri akibat keterbatasan digit yang
tersedia. Ini biasanya akan berkaitan dengan galat pemotongan dan galat pembulatan.
4. Galat yang ditimbulkan oleh hampiran oleh suatu bentuk formulasi atau rumusan matematika. Bentuk-bentuk ungkapan matematika yang cukup sulit atau
kompleks biasanya digunakan suatu pendekatan dengan polinomial atau metode
tertentu. Akibatnya, galat aka muncul.
Pertimbangkan evaluasi integral dari fungsi berikut,
1
I=
2
ex dx
0
Fungsi ini tidak mempunyai derivatif, jadi secara eksplisit fungsi ini tidak dapat diintegralkan. Oleh karena itu, langkah yang dapat diambil adalah denga melakukan
pendekatan, sala satunya adalah pendekatan dengan menggunakan deret Taylor,
2
ex ≈ 1 + x2 +
sehingga
1
2!
3!
4!
+ 6+ 8
4
x
x
x
2!
3!
4!
+ 6+ 8
4
x
x
x
0
dan bentuk di atas dapat dengan meudah dievaluasi. Galat pada persamaan diI≈
1 + x2 +
atas disebut galat pendekatan matematika.
Kehilangan Angka Penting Galat
Untuk memahami pengertian kehilangan bilangan galat, perhatikan persoalan berikut.
Diberikan suatu fungsi,
√
√
f (x) = x x + 1 − x
(2.2)
24
Bab 2 Analisis Galat
untuk sembarang bilangan x. Jika kita ambil beberapa nilai x yang terus membesar dan
menggunakan enam (6) angka penting, maka hasil dari perhitungan komputer diperlihatkan pada Tabel Dari tabel diperoleh bahwa, galat semakin besar seiring membe-
Tabel 2.1 Nilai-nilai persamaan (2.2) menggunakan enam angka
x
f (x) komputasi
1
10
100
1000
10000
100000
0,414210
1,54340
4,99000
15,8000
50,0000
100,000
f (x) sejati
0,414114
1,54347
4,98756
15,8074
49,9988
158,113
sarnya nilai x. Hal ini terjadi karena terjadi kehilangan angka penting pada perhitungan
persamaan tersebut. Misalkan kita ambil x = 100, maka
√
x+1−
√
x=
√
101 −
√
100 = 0, 0499000
(2.3)
Perhitungan pada persamaan (2.3) kehilangan angka penting galat. Tiga angka akurasi
√
√
√
dari x + 1 = 101 hilang karena adanya operasi pengurangan oleh sqrtx = 100.
Kehilangan akurasi ini disebabkan oleh bentuk fungsi f (x) dan keterbatasan aritmetik
pada komputer/kalkulator.
Untuk itu, langkah yang paling umum dilakukan adalah dengan mengubah ben√
tuk f (x). Misalkan f (x), di mana penyebut dan pembilang dikalikan dengan x + 1 +
√
x, dan kita peroleh,
√
√
√
√
x+1+ x
x+1+ x
·√
f (x) = x
√
1
x+1+ x
1
= x√
√
x+1+ x
x
= √
√
x+1+ x
(2.4)
2.2 Sumber Galat
25
Bentuk f (x) terakhir tidak kehilangan angka penting galat jika dievaluasi. Jika kita
ambil x = 100, maka
100
100
√
=
20,
0499
100 + 100
= 4, 98756
f (100) =
√
Untuk menghindari kehilangan angka penting pada galat, maka ungkapan-ungkapan
matematik di ubah sedemikan rupa sehingga tidak ada operasi pengurangan diantara
dua bilangan yang hampir sama nilainya. Untuk lebih jelasnya, perhatikan kembali
contoh berikut ini.
Contoh 2.3
Diberikan sebuah fungsi berikut.
f (x) =
1 − cos(x)
x2
(2.5)
untuk nilai x mendekati 0.
Penyelesaian:
Fungsi f (x) pada persamaan di atas akan kehilangan angka penting apabila nilai x
menjadi kecil. Perbandingan nilai eksak dan hasil perhitungan komputer (karena keterbatasan digit) diperlihatkan pada Tabel (2.5). Pada saat kita mengevaluasi fungsi
Tabel 2.2 Nilai-nilai persamaan (2.5) menggunakan enam angka
x
f (x) komputasi
0.1
0.01
0.001
0.0001
0.00001
0,4995834800
0,4999950000
0,5001000000
0,5100000000
0,0000000000
f (x) sejati
0,4995834722
0,4999958333
0,4999999583
0,4999999996
0,5000000000
f (0, 01), makak komputer akan menghitung,
cos(0, 01) = 0, 9999500005
26
Bab 2 Analisis Galat
dengan sembilan angka penting akurasinya, selanjutnya
1 − cos(0, 01) = 1, 0000000000 − 0, 9999500005
= = 0, 0000499995
Hasil operasi pengurangan kedua bilangan hanya menghasilkan lima (5) angka
penting, dan kehilangan empat (4) angka penting. Pembagian dengan x2 = 0, 0001
diberikan pada tabel 2.2).
Untuk menghindari kehilangan angka penting, dapat dilakukan dengan mengubah f (x) ke dalam betuk rumusan yang lain, dengan tujuan menghindari pengurangan dua buah bilangan yang hampir sama nilainya.
Salah satu alternatif yang dapat digunakan adalah deret Taylor. Jika kita ambil
pendekatan deret Taylor sampai orde ke-6 untuk cos(x),
cos(x) = 1 −
x2 x4 x6
+
−
+ R6 (x)
2!
4!
6!
dan
R6 (x) =
x8
cos(ζ)
8!
dengan ζ adalah bilangan tak diketahui terletak diantara 0 dan x. Oleh karena itu,
f (x) =
=
x2 x4 x6
1
+
−
+ R6 (x)
1
−
1
−
x2
2!
4!
6!
x2 x4 x6
1
−
+
−
cos(ζ)
2!
4!
6!
8!
Selanjutnya akan kita evaluasi fungsi f (x),
untuk x = 0, maka
f (0) =
untuk |x| ≤ 0, 1, maka
f (x) ≈
dengan keakurasian
1
2
x2 x4
1
−
+
2!
4!
6!
x6
10−6
cos(ζ) ≤
= 2, 5 × 10−11
8!
8!
Ini adalah cara yang cukup baik untuk mengevaluasi fungsi pada persamaan (2.5).
2.2 Sumber Galat
27
Contoh 2.4
Tentukan rumusan yang tepat agar tidak kehilangan angka penting untuk fungsi berikut
untuk tiga angka penting.
x2 + 80x + 1 = 0
Penyelesaian:
Dengan menggunakan rumus kuadratik diperoleh,
√
−b ± b2 − 4ac
x1 , x2 =
2a
−0, 800 × 102 ± 0, 640 × 104 − 0, 400 × 101
=
0, 200 × 101
−0, 800 × 102 ± 0, 640 × 104 − 0, 00 × 104
=
0, 200 × 101
√
2
−0, 800 × 10 ± 102 0, 640
=
0, 200 × 101
−0, 800 × 102 ± 102 × 0, 800
=
0, 200 × 101
Dari perhitungan di atas diperoleh,
x1 =
−0, 800 × 102 − 102 × 0, 800
= −0, 800 × 102
0, 200 × 101
x2 =
−0, 800 × 102 + 102 × 0, 800
= 0, 000 × 10−9
0, 200 × 101
dan
Dari hasil yang diperoleh, terlihat bahwa x2 sangat besar, sehingga kita perlu
mencari formulasi untuk menentukan akar-akar persamaan kuadratik tersebut. untuk
x1 , kita gunakan rumusan
x1 =
−b −
√
b2 − 4ac
,
2a
dan untuk x2 kita gunakan rumusan
x2 =
c
ax1
Dengan menggunakan bentuk ungkapan yang terakhir diperoleh,
x2 =
c
ax1
28
Bab 2 Analisis Galat
1
−0, 800 × 102
= −0, 125 × 10−1
=
Untuk membuktikan bahwa x1 dan x2 yang diperoleh adalah akar-akar persamaan
kuadratik, akan kita uji,
(x − x1 )(x − x2 ) = (x − (−0, 800 × 102 ))(x − (−0, 125 × 10−1 ))
= x2 + 80x + 1
Dari contoh soal di peroleh bahwa nilai b = 80 dan 4ac = 4 sehingga selisih b2
√
dengan b2 − 4ac memberikan nilai digit signifikan (tidak ada kehilangan digit).
Contoh 2.5
Diberikan suatu fungsi berikut,
f (x) = (x + )2/3 − x2/3
dengan ≤ 0, 001. Ubah sedemikian rupa fungsi f (x) sehingga tidak terjadi operasi
pengurang dengan dua angka yang hampir sama!
Penyelesaian:
Untuk menghindari terjadinya pengurangan di antara dua bilangan yang nilainya hampir sama adalah dengan mengalikan penyebut dan pembilang dengan (x + )2/3 + x2/3 ,
sehingga
f (x) = (x + )2/3 − x2/3 ×
(x + )2/3 − x2/3 =
2.3
(x + )2/3
2
(x + )2/3 + x2/3
(x + )2/3 + x2/3
− (x2/3 )2
(x + )2/3 + x2/3
Sumber Galat Numerik
a. Galat Pemotongan (Truncation Error)
Galat pemotongan biasanya mengacu kepada penggunaan hampiran sebagai pengganti
2.3 Sumber Galat Numerik
29
formula eksak. Maksudnya, ungkapan matematika yang lebih kompleks ”diganti” dengan formula yang lebih sederhana. Untuk penyederhanaan permasalahan biasanya perhatian hanya ditujukkan pada beberapaa suku dari deret taylor, sedangkan suku lainnya
diabaikan. Pengabaian ini menyebabkan terjadinya galat, yang biasa disebut galat pemotongan. Tipe galat pemotongan ini bergantung kepada metode komputasi yang digunakan untuk penghampiran. Misalkan, diberikan fungsi, f (x) = cos(x) yang dihampiri
dengan deret Taylor untuk x0 = 0 sampai orde ke-6,
x2 x4 x6 x8 x10
+
−
−
+ ···
cos(x) = 1 −
+
2! 4!
6! 8! 10!
nilai hampiran galat pemotongan
x2 x4 x6
+
−
+ R6 (x)
= 1−
2!
4!
6!
Jumlah suku-suku pada galat pemotongan tidak dapat dihitung secara pasti, tetapi
dapat dihampiri dengan rumus suku sisa pada persamaan (1.1), sehingga galat pemotongan orde ke-6 untuk cos(x) adalah
R6 (x) =
x3
cos(ξ), 0 < ξ < x
7!
Nilai R6 yang tepat tidak pernah kita peroleh, karena kita tidak mengetahui
nilai ξ yang sebenarnya. Untuk itu, yang dapat dilakukan adalah menentukan nilai
maksimum dari galat pemotongan.
Contoh 2.6
Gunakan deret Taylor orde 4 disekitar x0 = 1 untuk menghampiri ln(0, 9) dan berikan
taksiran untuk galat pemotongan maksimum yang dibuat.
Penyelesaian:
Jika f (x) = ln(x), maka turunannya adalah,
f (x) = ln(x)
→ f (1) = 0,
f (x) = 1/x
→ f (1) = 1,
30
Bab 2 Analisis Galat
..
.
f (4) (x) = −6/x4
→ f (4) (1) = −6,
f (5) (x) = 24/x5
→ f (5) (ξ) = 24/ξ 5
Deret Taylor untuk fungsi f (x) = ln(x) orde 4,
ln(x) = (x − 1) −
(x − 1)2 (x − 1)3 (x − 1)4
+
−
+ R4 (x)
2
3
4
dan untuk ln(0, 9), deret Taylornya adalah,
(−0, 1)2 (−0, 1)3 (−0, 1)4
+
−
+ R4 (x)
2
3
4
= −0, 1053583 + R4 (x)
ln(0, 9) = −0, 1 −
dan galat pemotongan R4 (x) diberikan oleh,
24 (−0,˙ 1)5
|R4 (0, 9) < max 5 ξ
5!
dan nilai max|24/ξ 5 | di dalam selang 0, 9 < ξ < 1 terletak pada ξ = 0, 9, maka
24 (−0,˙ 1)5
0, 95 5!
|R4 (0, 9) < max b. Galat Pembulatan
Perhitungan di dalam permasalahan numerik hampir sebagaian besar menggunakan
bilangan ril. Oleh karena keterbatasan komputer di dalam menyediakan bilangan ril,
sehingga tidak semua bilangan ril dapat disajikan. Akibatnya, muncul galat yang diakibatkan oleh pemotongan digit bilangan. Galat yang demikian disebut galat pembulatan.
Sebagai contoh, hasil bagi 2/3 menghasilkan nilai 0, 6666666666 . . .. Di dalam
mesin komputer, bilangan real seperti ini tidak dapat disajikan secara tepat. Komputer
hanya mampu menyajikan sejumlah digit (bit). Bilangan real yang panjangnya melebihi
jumlah digit yang dapat direpresentasikan oleh komputer akan dibulatkan ke bilangan
terdekat.
Misalnya, komputer hanya dapat merepresenatasikan bilangan real 0, 6666666666 . . .
ke dalam 6 digit berarti, maka representasi bilangan 1/6 = 0, 6666666666 . . . di komputer 6-digit adalah0, 666667.
2.3 Sumber Galat Numerik
31
c. Galat Total
Galat akhir dari suatu perhitungan secara numerik merupakan jumlah galat pemotongan dan galat pembulatan. Misalkan deret Taylor menghampiri cos(x) di x0 = 0 sampai
orde 4,
x2 x4 x6 x8 x10
+
−
+
−
+ ···
2!
4!
6!
8!
10!
x2 x4
= 1−
+
− +R4 (x)
2!
4!
cos(x) = 1 −
Untuk cos(0, 2) diperoleh,
cos(0, 2) ≈ 1−
(1)
0, 22 0, 24
+
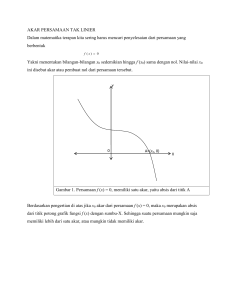
= 0, 9800666666666 . . . ≈ 0, 98006667 (8 digit penting)
2
24
(2)
Galat pada (1) adalah galat pemotongan karena cos(0, 2) dihampiri sampai orde 4, dan
galat pada (2) adalah galat pembulatan (hasil hampiran dibulatkan sampai 8 digit penting).
Contoh 2.7
Evaluasi fungsi
f (x) = x3 − 6x2 + 3x − 0, 149
(2.6)
pada x = 4, 71 dengan menggunakan tiga digit aritmetik
Penyelesaian:
Dari perhitungan diperoleh nilai-nilai f (4, 71) yang ditunjukkan pada Tabel Dari Tabel
Tabel 2.3 Nilai-nilai persamaan (2.6) menggunakan tiga digit aritmetik
Nilai
x
x2
x3
6x2
3x
Ecxact
tiga digit(chooping)
tiga digit(rounding)
4,71
4,71
4,71
22,1841
22,1
22,2
104,487111
104
105
133,1046
132
133
14,13
14,1
14,1
32
Bab 2 Analisis Galat
di atas dapat diperoleh nilai-nilai, nilai sejati :
f (4, 71) = 104, 487111 − 133, 1046 + 14, 13 − 0, 149 = −14, 636489
Tiga digit (galat pemotongan/chooping error):
f (4, 71) = 104 − 132 + 14, 1 − 0, 149 = −14, 0
Tiga digit (galat pembulatan/rounding error):
f (4, 71) = 105 − 133 + 14, 1 − 0, 149 = −14, 0
Jadi galat relatif tiga digit dari kedua sumber galat adalah
−14, 63648 + 14, 0 ≈ 0, 04
−14, 636489 Galat relatif yang dihasilkan dari evaluasi fungsi secara langsung bernilai cukup besar.
Untuk itu, dapat diambil alternatif cara untuk memperkecil galat relatif tersebut. Salah
satunya adalah menggunakan perkalian bersarang, sehingga persamaan (2.6) dibentuk
menjadi,
f (x) = x63 − 6x2 + 3x − 0, 149 = ((x − 6)x + 3)x − 0, 149
Dengan mengevaluasi fungsi dengan perkalian bersarang, galat relatif diberikan oleh,
−14, 636489 + 14, 5 ≈ 0, 0093
−14, 636489
tiga digit (chopping): −14, 636489 + 14, 6 ≈ 0, 0025
tiga digit (rounding) : −14, 636489
Perkalian bersarang dapat mereduksi galat relatif untuk pendekatan chopping,
sedangkan untuk pendekatan rounding lebih baik lagi dan dapat mereduksi galat relatif
sampai 90
2.4
Orde Hampiran
Di dalam metode numerik, fungsi f (x) yang rumit sering digantikan dengan
fungsi hampiran yang lebih sederhana. Misalkan f (h) dihampiri dengan fungsi p(h).
Jika |f (h)−p(h)| ≤ M |hn | dengan M adalah konstanta real dan M > 0, maka dikatakan
p(h) menghampiri f (h) dengan orde penghampiran O(hn ) dan ditulis,
f (h) = p(h) + O(hn )
2.4 Orde Hampiran
33
dan O(hn ) dapat diartikan sebagai orde galat hampiran fungsi. Karena h umumnya
cukup kecil, sehingga semakin tinggi nilai n maka galat akan semakin kecil, yang berarti semakin teliti penghampiran fungsinya. Metode yang berorde O(h2 ) lebih teliti
hasilnya daripada metode yang berorde O(h). Ketelitian juga bergantung kepada nilai
h. Misalnya, Pada metode orde O(h3 ), jika ukuran h baru dijadikan setengah kali h
semula, maka galat baru menjadi seperdelapan kali galat semula.
Andaikan suatu fungsi dihampiri oleh deret Taylor,
xi+1 = xi + h, i = 0, 1, 2, . . .
adalah titi-titik selebar h, maka hampiran f (xi+1 ) disekitar xi adalah
(xi+1 − xi ) (xi+1 − xi )2
f (xi ) +
f ”(xi ) + · · ·
1!
2!
(xi+1 − xi )n (n)
f (xi ) + Rn (xi+1 )
+
n!
h
h2
hn (n)
= f (xi ) + f (xi ) + f ”(x2 ) + · · · +
f (xi ) + Rn (xi+1 )
1!
2!
n!
f (xi+1 ) = f (xi ) +
(2.7)
dengan
hn+1 (n+1)
f
(t)
(n + 1)!
= O(hn+1 ), xi < t < xn+1
Rn (xi+1 ) =
Jadi, kita dapat menuliskan kembali persamaan (2.7) dalam bentuk,
f (xi+1 ) =
n
hk
k=0
k!
f (k) (xi ) + O(hn+1 )
Sebagai contoh.
eh = 1 + h +
h2
2!
ln(x + 1) = x −
sin(h) = h −
h3
3!
+
x2
2
+
h3
3!
+
h5
5!
+
x3
3
+
h4
4!
+ O(h5 )
x4
x5
6
4 + 5 + O(h )
O(h7 ), (bukan O(h6 ),
−
karena suku orde ke 6 adalah 0)
Contoh 2.8
Pertimbangkan ekspansi deret Taylor berikut.
eh = 1 + h +
h2 h3
+
+ O(h4 )
2!
3!
(2.8)
34
Bab 2 Analisis Galat
dan
cos(h) = 1 −
h2 h4
+
+ O(h6 )
2!
4!
Hitunglah orde hampiran dari jumlah dan perkalian keduanya. Penyelesaian:
Untuk penjumlahan,
eh + cos(h) =
h2 h3
h2 h4
+
+ O(h4 ) + 1 −
+
+ O(h6 )
1+h+
2!
3!
2!
4!
= 2+h+
Oleh karena
O(h4 ) +
h3
h4
+ O(h4 ) +
+ O(h6 )
3!
4!
h4
= O(h4 )
4!
dan O(h4 ) + O(h6 ) = O(h4 )
maka
eh + cos(h) = 1 + h +
h2 h3
+
2!
3!
dan orde hampirannya adalah O(h4 ). Sedangkan perkaliannya,
h
(e )(cos(h)) =
h2 h3
+
+ O(h4 )
1+h+
2!
3!
=
h2 h3
+
1+h+
2!
3!
h2 h4
+
+ 1−
2!
4!
= 1+h−
h2 h4
+
+ O(h6 )
1−
2!
4!
h2 h4
h2 h3
+ + + 1+h+
+
1−
2!
4!
2!
3!
h7
h3 5h4 h5 h6
−
−
+
+
+ O(h4 ) + O(h6 ) + O(h4 )O(h6 )
3
24
24 48 144
O(h4 )O(h6 ) = O(h10 )
−
O(h6 )
O(h4 ) + O(h4 )O(h6 )
Oleh karena
dan
h7
5h4 h5 h6
−
+
+
+ O(h4 ) + O(h6 ) + O(h4 )O(h6 ) = O(h4 )
24
24 48 144
maka
eh cos(h) = 1 + h −
h3
+ O(h4 )
3
2.5 Perambatan Galat
2.5
35
Perambatan Galat
Bilangan titik kambang adalah bilangan yang disajikan dalam bentuk sejumlah
digit berarti yang sudah tetap, yaitu
±d1 d2 d3 d4 d5 . . . dn × B p
dengan:
d1 d2 d3 d4 d5 . . . dn adalah digit atau bit mantisa yang nilainya 0 sampai B − 1,
n adalah panjang digit (bit) mantisa
B adalah basis sistem bilangan yang dipakai
p adalah pangkat (berupa bilangan bulat)
Misalnya, bilagan real 245,7654 dinyatakan dalam bentuk 0, 2457654 × 103
Galat yang dikandung dalam bilangan titik kambang merambat pada hasil komputasi. Misalkan terdapat dua bilangan a dan b dengan nilai hampiran masing-masing
â dan b̂. Jika galt dari a dan b masing-masing a dan b , maka dapat ditulis,
a = â + a
dan b = b̂ + b
Jika diberikan operasi penjumlah pada dua bilangan tersebut,
a + b = (â + a ) + (b̂ + b )
= (â + b̂) + (a + b )
Jika operasi aritmetika dilakukan secara terus-menerus dalam perhitungan komputasi,
maka galat akan merambat dan terjadi penumpukan galat yang besar kemungkinan
mengakibatkan penyimpangan hasil terhadap nilai sebernarnya.
36
Bab 2 Analisis Galat
Latihan
2.2
1. Kadang-kadang kehilangan signifikasi galat dapat dihindari dengan menyusun
kembali suku-suku dari suatu fungsi atau menggunakan identitas dari trigonometri
atau aljabar. Tentukan rumusan yang sesuai untuk fungsi-fungsi berikut untuk
menghindari kehilangan angka penting.
a. ln(x + 1) − ln(x) untuk x yang cukup besar
√
b. x2 + 1 − x untuk x yang cukup besar
c. cos2 (x) − sin2 (x) untuk x ≈
d.
1+cos(x)
2
π
4
untuk x ≈ π
2. Jika diberikan p = p̂ + p , q = q̂ + q , r = r̂ + r , bagaimana pendapat anda untuk
kasus berikut ini.
a. Jumlah tiga bilangan p + q + r
b. Perkalian tiga bilangan pqr
3. Diberikan ekspansi deret Taylor,
1
= 1 + h − h2 + h3 + O(h4 )
1−h
dan
cos(h) = 1 −
h2 h4
+
+ O(h6 )
2!
4!
Hitunglah orde hampiran untuk penjumlahan dan perkalian
4. Diberikan ekspansi deret Taylor,
eh = 1 + h +
h2 h3 h2
+
+
+ O(h5 )
2!
3!
2!
dan
sin(h) = h −
h3
+ O(h5 )
3!
Hitunglah orde hampiran untuk penjumlahan dan perkalian
2.5 Perambatan Galat
37
5. Asumsikan bahwa a = 0 dan b2 − 4ac > 0 dan pertimbagkan persamaan kuadratik
ax2 + bx + c = 0 yang mana akar-akarnya dihitung dengan menggunakan rumus,
√
−b + b2 − 4ac
x1 =
2a
dan
√
b2 − 4ac
2a
Tunjukkan bahwa akar-akar persamaan tersebut juga dapat dihitung dengan mengx2 =
−b −
gunakan rumus,
x1 =
−2c
√
b + b2 − 4ac
dan x2 =
−2c
√
b − b2 − 4ac
6. Dengan menggunakan rumus pada soal di atas, hitunglah nilai x1 dan x2 untuk
persamaan kuadratik berikut.
a. x2 − 1.000.001x + 1 = 0
b. x2 − 10.000.001x + 1 = 0
c. x2 − 100.000.001x + 1 = 0
d. x2 − 1000.000.001x + 1 = 0
7. Dengan menggunakan tiga digit aritmetika, hitunglah
a. x2 + 100x − 4 = 0
b. x2 − 60x + 2 = 0
c.
1 2
3x
−
123
4 x
+
1
6
d.
1 2
3x
+
123
4 x
−
1
6
e. 1, 002x2 − 11, 01x + 0, 01265
f. 1, 002x2 + 11, 01x + 0, 01265
8. Turunkan rumusan berikut ini,
Ax2 + 2Bx + C = 0
dan temukan rumusan yang dapat dilakukan agar akar-akar fungsi tersebut mempunyai galat yang cukup kecil
38
Bab 2 Analisis Galat
9. evaluasi fungsi-fungsi berikut jika mendekati 0
1
1
−
x+1 x
b. cos(x + ) − cos(x)
√
c. (x + 1)1/3 − x1/3
a.
1
1
d. √ − √
x
x+1
e. tan(x + ) − tan(x)
2
1
1
− +
f.
x+1 x x−1
BAB 3
PENYELESAIAN SISTEM LINEAR
Sistem dari persamaan linear sering kita jumpai dibeberapa bidang terapan, misalnya
pada persoalan matematika, statistik, fisika, biologi, rekayasa, sains sosial dan bisnis.
Pada bab ini dibahas bagaimana menyelesaikan persoalan-persoalan sistem persamaan
linear serentak yang berasal dari dunia nyata.
3.1
konsep Dasar Sistem Persamaan Linear
Salah satu topik yang dipelajari pada aljabar linear elementer adalah menyele-
saikan dua buah persamaan linear berikut,
ax + by = c
dx + ey = f
(3.1)
Koefisien-koefisien a, b, . . . f adalah konstanta yang diberikan, tugas kita adalah menentukan nilai x dan y. Dengan menggunakan metode substitusi atau metode eleminasi,
maka persamaan (4.2) dapat diselesaikan. Persoalan muncul ketika persamaan linear
yang dilibatkan sangat banyak, maka metode substitusi atau metode elemeninasi akan
mengalami kesulitan.
Jika terdapat n buah persamaan linear, dengan x1 , x2 , . . . xn , dapat dibentuk
sebuah sistem persamaan linear sebagai berikut.
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
a21 x1 + a22 x2 + a23 x3 + · · · + a2n xn = b2
..
..
..
..
..
.
.
.
.
.
an1 x1 + an2 x2 + an3 x3 + · · · + ann xn = bn
(3.2)
40
Bab 3 Penyelesaian Sistem Linear
Untuk mempermudah penyelesaian persamaan linear yang melibatkan n buah persamaan, maka dengan menggunakan matriks, maka persamaan (3.3) dapat dibentuk
menjadi,
Ax = b
di mana
⎛
⎜
⎜
A=⎜
⎜
⎝
a11
a21
..
.
· · · a1n
· · · a2n
..
.
a12
a22
..
.
an1 an2 · · · ann
⎞
⎟
⎟
⎟,
⎟
⎠
(3.3)
⎛
⎜
⎜
x=⎜
⎜
⎝
x1
x2
..
.
⎞
⎟
⎟
⎟,
⎟
⎠
⎛
⎜
⎜
b=⎜
⎜
⎝
xn
b1
b2
..
.
⎞
⎟
⎟
⎟
⎟
⎠
bn
Andaikan bahwa n = 1, maka persamaan (??) menjadi,
a11 x1 = b1
(3.4)
Jika a11 = 0, maka persamaan (3.4) mempunyai solusi unik, yaitu x1 = b1 /a11 , tetapi
jika a11 = 0, maka persamaan (3.4) tidak mempunyai penyelesaian untuk b1 = 0, dan
untuk kasus b1 = 0 maka x1 adalah penyelesaian untuk setiap nilai x1 .
Dari persamaan (3.3), diketahui bahwa matriks x merupkan penyelesaian dari
sistem persamaan linear (3.3). Jika matriks A adalah matriks non-singular (mempunyai
invers), maka penyelesaian persamaan (3.3) dapat ditulis dalam bentuk,
x = A−1 b
(3.5)
Untuk kasus n = 1, maka A−1 = 1/a11 sehingga penyelesaian dari (3.3) adalah
x1 =
1
b1
a11
Contoh 3.1
Selesaikan sistem persamaan linear berikut.
2x1 + 3x2 = 8
5x1 + 4x2 = 12
Penyelesaian:
Sistem persamaan linear di atas dapat diubah ke dalam bentuk matriks,
2 3
5 4
x1
x2
=
8
13
3.1 Konsep Dasar Sistem Persamaan Linear
41
dimana
A=
2 3
5 4
,
x=
x1
x2
,
b=
8
13
Oleh karena matriks koefisien merupakan mariks non-singular (det(A) = 0 ),
maka sistem persamaan linear di atas mempunyai penyelesaian unik, yaitu
x = A−1 b
dan diperoleh
x1 = 1,
x2 = 2
atau
x=
1
2
Contoh 3.2
selesaikan sistem persamaan linear berikut.
2x1 + 3x2 = 4
4x1 + 6x2 = 7
Sistem persamaan linear di atas dapat diubah ke dalam bentuk matriks,
2 3
4 6
x1
x2
=
4
7
dimana
A=
2 3
4 6
,
x=
x1
x2
,
b=
4
7
Det(A) = 0, maka matriks A adalah matriks singular, dan oleh karena
b=
4
7
maka sistem persamaan linear di atas tidak mempunyai penyelesaian untuk x1 dan x2
Seandaikan jika,
b=
4
8
maka dua persamaan pada sistem persamaan linear adalah sama, karena
2x1 + 3x2 = 4
dan
(2)2x1 + (2)3x2 = (2)4
42
Bab 3 Penyelesaian Sistem Linear
sehingga penyelesaian diperoleh hanya melibatkan satu persamaan yaitu,
2x1 + 3x2 = 4
dengan penyelesaian
x1 =
4 − 3c
,
2
x2 = c
untuk semua bilangan real c, sehingga penyelesaian dari sistem persamaan linear tidak
berhingga.
3.2
Elemninasi Gauss
Metode yang paling sering digunakan untuk menyelesaian sistem non-singular
dari suatu sistem persamaan linear adalah eleminasi Gauss. Metode ini cukup sederhana dan efektif. Ide pokok pada metode ini adalah bagaimana mengeleminasi variabelvariabel x1 , x2 , . . . , xn untuk memanipulasi persamaan (3.3) sehingga diperoleh bentuk
yang sederhana, selanjutnya akan mudah untuk diselesaikan. Beberapa operasi matematika yang biasa digunakan pada metode tersebut adalah perkalian dengan konstanta
bukan nol, pengurangan suatu persamaan dengan persamaan lainnya, dan mengubah
baris.
Pandang kembali sistem persamaan linear (??) dalam bentuk,
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
a21 x1 + a22 x2 + a23 x3 + · · · + a2n xn = b2
..
..
..
..
..
.
.
.
.
.
(1)
an1 x1 + an2 x2 + an3 x3 + · · · + a(1)
nn xn = bn
(1)
Misalkan a11 = 0, maka kita dapat mengeleminasi x1 dari setiap persamaan den(1)
(1)
gan mengalikan ai1 /a11 terhadap persamaan pertama. Hasil dari elemeninasi dilambangkan dengan superskrip 2. Pada setiap persamaan bentuk,
(1)
mi1 =
ai1
(1)
a11
dan
(2)
(1)
(1)
aij = aij − mij a1j ,
j = 1, 2, . . . , n
3.2 Eleminasi Gauss
43
serta
(2)
bi
(1)
(1)
= bi − mi1 b1
(2)
Perkalian persamaan pertama ditentukan untuk membuat ai1 = 0 (elemninasi
x1 dari persamaan ke-i, untuk i = 2, 3, . . . , n. Selanjutnya susun kembali matriks hasil
eleminasi x1 , yaitu
(1)
(1)
(1)
(1)
(1)
(2)
(2)
(2)
(2)
(2)
(2)
(2)
(2)
(2)
(2)
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
a22 x2 + a23 x3 + · · · + a2n xn = b2
a32 x2 + a33 x3 + · · · + a3n xn = b3
..
..
..
..
.
.
.
.
(2)
an2 x2 + an3 x3 + · · · + a(2)
nn xn = bn
Selanjutnya eleminasi x2 dari persamaan ke-i untuk i = 3, 4, . . . , n. Misalkan
(2)
a22
= 0, maka untuk i = 3, 4, . . . , n kita ambil,
mi2 =
ai2
(2)
,
ai2
dan kemudian
(3)
(2)
(2)
aij = aij − mi2 a2j ,
j = 2, 3, . . . , n
dan
(3)
bi
(2)
(2)
= bi − mi2 b2
memberikan hasil,
(1)
(1)
(1)
(1)
(1)
(2)
(2)
(2)
(2)
(2)
(2)
(2)
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
a22 x2 + a23 x3 + · · · + a2n xn = b2
a33 x3 + · · · + a3n xn = b3
..
..
..
.
.
.
(2)
(2)
an3 x3 + · · · + a(2)
nn xn = bn
(3)
Eleminasi x3 dari persamaan i = 4, 5, . . . , n dengan memisalkan a33 = 0.
(1)
(2)
(3)
(n)
Elemen-elemen (a11 , a22 , a33 , . . . , ann disebut elemen pivot. Jika eleminasi dilakukan
44
Bab 3 Penyelesaian Sistem Linear
terhadap persamaan-persamaan linear sampai elemen-elelmen pivot hilang, maka akan
menghasilkan bentuk sistem persamaan linear
(1)
(1)
(1)
(1)
(1)
(2)
(2)
(2)
(2)
(3)
(3)
(3)
a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn = b1
a22 x2 + a23 x3 + · · · + a2n xn = b2
a33 x3 + · · · + a3n xn = b3
..
..
.
.
(3.6)
(n)
a(n)
nn xn = bn
Proses reduksi terhadap persamaan (3.3) menjadi (3.6) disebut eleminasi, dan koefisien
matriks pada persamaan (3.6) disebut matriks segitiga atas, yang ditulis
U = (uij )
yang mana uij = 0 , jika i > j atau ditulis
⎛
⎜
⎜
⎜
⎜
U=⎜
⎜
⎜
⎜
⎝
(1)
(1)
(1)
(1)
(1)
+ · · · + a1(n−1) + a1n
⎞
a11
+ a12
+ a13
0
+ a22
+ a23
(2)
(2)
+ · · · + a2(n−1) + a2n ⎟
⎟
0
..
.
0
+
+ a33
..
.
0
+ · · · + a3(n−1) + a3n
..
..
.
.
(3)
···
0
a3n
(2)
0
..
.
0
(2)
(3)
(3)
(3)
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Penyelesaian untuk x1 , x2 , . . . , xn dilakukan dengan mensubstitusikan kembali. Jika
(n)
ann = 0, maka penyelesaian untuk xn adalah
(n)
bn
xnn =
(n)
ann
selanjutnya nilai xn digunakan untuk menyelesaian xn−1 ,
(n−1)
(n−1)
(n−1)
(n−1)
a(n−1)(n−1) xn−1 + a(n−1)n x(n−1)n = bn−1
atau
(n−1)
(n−1)
(n−1)
(n−1)
a(n−1)(n−1) xn−1 + a(n−1)n x(n−1)n = bn−1
atau
(n−1)
(n−1)
a(n−1)(n−1) xn−1 + a(n−1)n
(n)
bn
(n)
ann
(n−1)
= bn−1
x(n−1)(n−1) =
1
a(n−1)(n−1)
bn−1 −
(n)
(n−1) bn
a(n−1)n (n)
ann
3.2 Eleminasi Gauss
45
Jika langkah tersebut secara menerus dilakukan, maka dapat ditulis secara umum,
⎛
⎞
n
1
(k)
(k)
akj xj ⎠
xk = (k) ⎝ak −
akk
j=k+1
(3.7)
Contoh 3.3
selesaikan sistem persamaan linear berikut.
1
x1 + x2 + x3 =
x1 + 2x2 + 4x3 = −1
x1 + 3x2 + 9x3 =
1
(3.8)
Elemenasi x1 pada persamaan kedua dan ketiga dengan mengurangkan persamaan pertama terhadap kedua persamaan, diperoleh,
x1 +
x2 + x3 =
1
x2 + 3x3 = −2
2x2 + 8x3 =
0
(3.9)
Eleminasi x2 pada persamaan ketiga dengan mengurankan 2 kali persamaan kedua
terhadap persamaan ketiga, diperoleh
1
x1 + x2 + x3 =
x2 + 3x3 = −2
2x3 =
4
(3.10)
Dengan menggunakan algoritma substitusi-ulang diperoleh,
4
=2
2
= −3(2) − 2 = −8
x3 =
x2
x1 = 6 + 1 = 7
Contoh 3.4
Selesaikan sistem berikut
1, 133x1 + 5, 281x2 = 6, 414
24, 14x1 − 1, 210x2 = 22, 93
(3.11)
Kalikan m21 = 24, 14/1, 133 = 21, 31 terhadap baris pertama dan kurangkan terhadap
baris kedua, dan dengan menggunakan empat digit perhitungan diperoleh koefisien
46
Bab 3 Penyelesaian Sistem Linear
baru,
(2)
a22
= −1, 210 − 21, 31(5, 281) = −1, 210 − 112, 5
= −113, 7
(2)
a23
= 22, 93 − 21, 31(6, 414) = 22, 93 − 136, 7
= −113, 8
dan diperoleh sistem segitiga atas,
1, 133x1 + 5, 281x2 =
6, 414
− 113, 7x2 = −113, 8
(3.12)
Dengan menggunakan algoritma substitusi-ulang, diperoleh
−113, 8
= 1, 001
−113, 7
6, 414 − 5, 286
6, 414 − 5, 281(1, 001)
=
=
1, 133
1, 133
= 0, 9956
x2 =
x1
Penyelesaian dari sistem persamaan linear di atas adalah x1 = 1, 000 dan x2 =
1, 000. Untuk dapat menentukan solusi yang sebenarnya, maka dilakukan dengan mengubah baris, sehingga sistem yang baru adalah sebagai berikut.
24, 14x1 − 1, 210x2 = 22, 93
1, 133x1 + 5, 281x2 = 6, 414
(3.13)
Kalikan m21 = 1, 133/24, 14 = 0, 04693 terhadap baris pertama dan hasilnya kurangkan
terhadap baris kedua, dan diperoleh koefisien baru,
(2)
a22
= 5, 281 − 0, 04693(−1, 210) = 5, 281 + 0, 05679
= 5, 338
(2)
a23
= 6, 414 − 0, 04693(22, 93) = 6, 414 − 1, 076
= 5, 338
sehingga diperoleh sistem segitiga atas, yaitu
24, 14x1 − 1, 210x2 = 22, 93
5, 338x2 = 5, 338
(3.14)
3.2 Eleminasi Gauss
47
Dengan menggunakan algoritma substitusi-ulang diperoleh,
x2 = 5, 338/5, 338
x1
= 1, 000
22, 93 + 1, 210(1, 000)
=
24, 14
= 1, 000
Latihan
3.1
Tunjukkan bahwa Ax = b adalah ekivalen terhadap bentuk sistem segitiga atas atas
Ux = y dan tentukan penyelesaian.
2x1 + 4x2 − 6x3 = −4
1. x1 + 5x2 + 3x3 = 10
x1 + 3x2 + 2x3 =
5
2x1 + 4x2 − 6x3 = −4
3x2 + 6x3 = 12
3x3 =
3
x1 + x2 − 6x3 = 7
2. −x1 + 2x2 + 9x3 = 2
x1 − 2x2 + 3x3 = 10
x1 +
3.
2x1 − 2x2 + 5x3 = 6
2x1 + 3x2 + x3 = 13
−x1 + 4x2 − 4x3 = 3
4.
−5x1 + 2x2 − x3 = −1
x1 + 0x2 + 3x3 =
5
3x1 + x2 + 6x3 = 17
x2 − 6x3 = 7
3x2 + 15x3 = 9
12x3 = 12
2x1 − 2x2 +
5x2 −
−5x1 +
5x3 =
6
4x3 =
7
0, 9x3 = 1, 8
2x2 −
x3 = −1
0, 4x2 + 2, 8x3 = 4, 8
− 10x3 = −10
5. Tentukan parabola y = A + Bx − Cx2 yang melalui (1, 4), (2, 7) dan (3, 14)
6. Tentukan parabola y = A + Bx + Cx2 yang melalui (1, 6), (2, 5) dan (3, 2)
7. Tentukan parabola y = A + Bx + Cx2 yang melalui (1, 2), (2, 2) dan (4, 8).
8. Tentukan penyelesaian dari sistem linear berikut.
x1
2x1
5x1
−3x1
+ x2
− x2
+ 2x2
+ 0x2
+ 0x3
+ 5x3
+ x3
+ 2x3
+
+
+
+
4x4
0x4
2x4
6x4
=
3
=
2
=
5
= −2
48
Bab 3 Penyelesaian Sistem Linear
9. Tentukan solusi dari sistem linear berikut.
x1 − x2
2x1 − 3x2 − x3
2x2 + 2x3 + 3x4
2x3 − 4x4
= 7
= 9
= 10
= 12
10. Tentukan penyelesaian sistem linear berikut.
x1 +
2x1 −
3.3
x2
x2 + 5x3
3x2 − 4x3 + 2x4
2x3 + 6x4
=
5
= −9
= 19
=
2
Faktorisasi Matriks LU
Pada sub-bab sebelumnya, kita telah mempelajari bagaimana menyelesaikan sis-
tem persamaan linear dengan menggunakan metode eleminasi Gauss yang menghasilkan
segitiga atas. Pada pembahasan kali ini, kita akan memperkenalkan konsep faktorisasi
dari matriks koefisien A yang diberikan menjadi perkalian matriks segitiga-atas U dengan elemen-elemen diagonal tidak nol dan mariks segitiga bawah L yang mempunyai
elemen-elemen diagonal 1. Untuk mengilustrsikan, berikut diberikan contoh faktorisasi
matriks berukuran 4 × 4.
Definisi 3.1
Sebuah matriks non-singular A mempunyai faktorisasi triangular jika matriks tersebut
dapat dibentuk sebagai suatu perkalian matrik segigita bawah L dan matriks segitiga
atas U,
A = LU
(3.15)
atau ditulis dalam bentuk matriks
⎛
⎜
⎜
⎜
⎝
a11
a21
a31
a41
a12
a22
a32
a42
a13
a23
a33
a43
a14
a24
a34
a44
⎞
⎛
⎟ ⎜
⎟ ⎜
⎟=⎜
⎠ ⎝
1
0
0
m21
1
0
m31 m32
1
m41 m42 m43
0
0
0
1
⎞⎛
⎟⎜
⎟⎜
⎟⎜
⎠⎝
u11 u12 u13
0 u22 u23
0
0 u33
0
0
0
u14
u24
u34
u44
⎞
⎟
⎟
⎟ (3.16)
⎠
Oleh karena matrisk A adalah non-singular, menyebabkan ukk = 0 untuk semua k dan
elemen-elemen dari matriks L dan U masing-masing adalah mij dan uij .
3.3 Faktorisasi Matriks LU
49
Penyelesaian Sistem Linear
Misalkan matriks koefisien A untuk sistem linear Ax = b yang mempunyai
faktorisasi triangular (3.15), dan selanjutnya selesaikan bentuk,
LUX = B
(3.17)
yang diperoleh dengan mendefinsikan Y = U X dan selesaikan dua buah sistem, yaitu:
penyelesaiann untuk Y,
LY = B
(3.18)
UX = Y
(3.19)
dan penyelesaian untuk X,
Jika matriks Y didefinisikan,
⎛
⎜
⎜
⎝
Y=⎜
y1
y2
y3
y4
⎞
⎟
⎟
⎟
⎠
maka bentuk sistem LY = B ditulis,
y1
m21 y1
m31 y1
m41 y1
+
+
y2
+ m32 y2 +
y3
+ m42 y2 + m43 y3 + y4
=
=
=
=
b1
b2
b3
b4
(3.20)
Selesaikan (3.20) untuk menentukan y1 , y2 , y3 dan y4 dan gunakan untuk menyelesaikan
sistem,
u11 x1 + u12 x2 + u13 x3 + u14 x4
u22 x2 + u23 x3 + u24 x4
u33 x3 + u34 x4
u44 x4
Contoh 3.5
Selesaikan sistem berikut.
4x1 + 3x2 − x3 = −2
−2x1 − 4x2 + 5x3 = 20
7
x1 + 2x2 + 6x3 =
=
=
=
=
y1
y2
y3
y4
(3.21)
50
Bab 3 Penyelesaian Sistem Linear
Penyelesaian:
Dari soal di atas, diperoleh matriks koefisiennya adalah
⎛
⎞
4
3 −1
⎜
⎟
A = ⎝ −2 −4 5 ⎠
1
2
6
Selanjutnya, kita akan mengkontruksi matriks koefisien A menjadi faktorisasi matriks
segitiga LU. Matriks L akan dikontruksi dari matriks identitas yang diletakan sebelah
kiri matriks A,
⎛
⎞⎛
⎞
1 0 0
4
3 −1
⎜
⎟⎜
⎟
A = ⎝ 0 1 0 ⎠ ⎝ −2 −4 5 ⎠
0 0 1
1
2
6
Baris 1 digunakan untuk mengeleminasi elemen-elemen A pada kolom 1 di bawah a11 .
Kalikan m21 = 0, 5 dan m31 = 0, 25 pada baris 1 yang kemudian kurangkan terhadap
baris 2 dan 3, diperoleh,
⎛
⎞⎛
⎞
1
0 0
4
3
−1
⎜
⎟⎜
⎟
A = ⎝ −0, 5 1 0 ⎠ ⎝ 0 −2, 5 4, 5 ⎠
0, 25 0 1
0 1, 25 6, 25
Baris 2 digunakan untuk mengeleminasi elemen-elemen A pada kolom 2 dibawah a22 .
Kalikan m32 = 0, 5 pada baris 2 yang kemudian kurangkan terhadap baris 3. Pengalinya
di masukan dalam matriks sebelah kiri, dan diperoleh matriks faktorisasi A, yaitu,
⎛
⎞⎛
⎞
1
0
0
4
3
−1
⎜
⎟⎜
⎟
1
0 ⎠ ⎝ 0 −2, 5 4, 5 ⎠
A = ⎝ −0, 5
0, 25 −0, 5 1
0
0
8, 5
Dari hasil faktorisasi matriks A, ini berarti
⎛
⎞
1
0
0
⎜
⎟
1
0 ⎠
L = ⎝ −0, 5
0, 25 −0, 5 1
⎛
Tentukan y1 , y2 dan y3 dengan menyelesaikan bentuk
B
⎞ ⎛ LY
⎞ = ⎛
⎞
1
0
0
y1
−2
⎜
⎟⎜
⎟
⎜
⎟
1
0 ⎠ ⎝ y2 ⎠ = ⎝ 20 ⎠
⎝ −0, 5
y3
0, 25 −0, 5 1
7
⎛
⎞
4
3
−1
⎜
⎟
dan U = ⎝ 0 −2, 5 4, 5 ⎠
0
0
8, 5
3.3 Faktorisasi Matriks LU
51
atau
y1
= −2
−0, 5y1 +
y2 = 20
7
0, 25y1 − 0, 5y2 + y3 =
Dengan menggunakan substitusi maju, diperoleh nilai-nilai y1 , y2 dan y3 , yaitu:
y1 = −2
y2 = 20 + 0, 5(−2) = 19
y3 = 7 − 0, 25(−2) + 0, 5(19) = 17
Selanjutnya tulis sistem,
UX
Y
⎞ = ⎛
⎞
4
3
−1
x1
−2
⎜
⎟⎜
⎟
⎜
⎟
⎝ 0 −2, 5 4, 5 ⎠ ⎝ x2 ⎠ = ⎝ 19 ⎠
x3
0
0
8, 5
17
⎛
⎞⎛
atau
4x1 +
3x2 −
x3 = −2
−2, 5x2 + 4, 5x3 = 19
8, 5x3 = 17
Gunakan substitusi mundur dan diperoleh,
x3 =
x2 =
x1 =
17
=2
8, 5
1
(19 − 4, 5(2)) = −4
−2, 5
1
(−2 − 3(−4)) = 3
4
Latihan
3.2
1. Selesaikan LY = B, UX = Y dan verifikasi bahwa B = AX untuk (a) BT =
(−4, 10, 5) dan (b) BT = (20, 49, 32), di mana A = LU adalah
⎛
⎞
⎛
2 4 −6
1
⎜
⎟ ⎜ 1
3 ⎠=⎝ 2
⎝ 1 5
1
1 3
2
2
⎞⎛
⎞
0 0
2 4 −6
⎟⎜
⎟
6 ⎠
1 0 ⎠⎝ 0 3
1
0 0
3
3 1
52
Bab 3 Penyelesaian Sistem Linear
2. Selesaikan LY = B, UX = Y dan verifikasi bahwa B = AX untuk (a) BT =
(7, 2, 10) dan (b) BT = (25, 35, 7), di mana A = LU adalah
⎛
⎞
⎛
⎞⎛
⎞
1
1 6
1
0 0
1 1 6
⎜
⎟ ⎜
⎟⎜
⎟
2 9 ⎠ = ⎝ −1
1 0 ⎠ ⎝ 0 3 15 ⎠
⎝ −1
1 −2 3
1 −1 1
0 0 12
3. Selesaikan LY = B, UX = Y dan verifikasi bahwa B = AX untuk (a) BT =
(6, 13, 3) dan (b) BT = (3; 1, 5; −1, 5), di mana A = LU adalah
⎛
⎞
⎛
⎞⎛
⎞
2 −2
5
1
0 0
2 −2
5
⎜
⎟ ⎜
⎟⎜
⎟
3
1 ⎠=⎝
1
1 0 ⎠⎝ 0
5 −4 ⎠
⎝ 2
−1
4 −4
−0, 5 0, 6 1
0
0 0, 9
4. Tentukan
⎛ faktorisasi
−5 2 −1
⎜
3
(a) ⎝ 1 0
3 1
6
matriks segitiga A = LU dari
berikut ini.
⎞
⎛ matriks-matriks
⎞
5. Tentukan
⎛ faktorisasi
4
2
1
⎜
5 −2
(a) ⎝ 2
1 −2
7
matriks segitiga A = LU dari
berikut ini.
⎞
⎛ matriks-matriks
⎞
⎟
⎠
(b)
⎟
⎠
(b)
1 0
3
⎟
3 1
6 ⎠
−5 2 −1
⎜
⎝
1 −2
7
⎟
2
1 ⎠
2
5 −2
⎜
⎝ 4
6. Selesaikan LY = B, UX = Y dan verifikasi bahwa B = AX untuk (a) BT =
(8, −4, 10, −4) dan (b) BT = (28, 13, 23, 4), di mana A = LU adalah
⎛
⎜
⎜
⎜
⎝
4
1
2
1
⎞
⎛
8
4
0
1
⎜ 1
5
4 −3 ⎟
⎟ ⎜ 2
⎟=⎜
3
1
3 ⎠ ⎝ 14
1
4 −2
2
4
0
1
2
3
1
3
⎞⎛
0 0
4
⎜ 0
0 0 ⎟
⎟⎜
⎟⎜
1 0 ⎠⎝ 0
− 12 1
0
8
3
0
0
⎞
4
0
3 −3 ⎟
⎟
⎟
4
4 ⎠
0
1
7. Tentukan faktorisasi matriks segitiga A = LU untuk matriks berikut ini.
⎛
⎜
⎜
⎜
⎝
1
1 0 4
2 −1 5 0
5
2 1 2
−3
0 2 6
⎞
⎟
⎟
⎟
⎠
8. Hukum Kirchhoff mengatakan bahwa jumlah arus yang masuk dan keluar adalah
sama, yang diberikan pada sistem persamaan linear berikut.
R3 I2 +
R4 I3 = E1
(R1 + R3 + R4 )I1 +
R3 I1 + (R2 + R3 + R5 )I2 −
R5 I3 = E2
R4 I1 −
R5 I2 + (R4 − R5 + R6 )I3 = 0
3.4 Metode Iterasi untuk Sistem Linear
53
Selesaikan sistem di atas untuk I1 , I2 dan I3 jika:
(a) R1 = 1, R2 = 1, R3 = 2, R4 = 1, R5 = 2, R6 = 4 dan E1 = 23, E2 = 29
(b) R1 = 1, R2 = 0, 75, R3 = 1, R4 = 2, R5 = 1, R6 = 4 dan E1 = 12, E2 = 21, 5
(c) R1 = 1, R2 = 2, R3 = 4, R4 = 3, R5 = 1, R6 = 5 dan E1 = 41, E2 = 38
3.4
Metode Iterasi untuk Sistem Linear
Pada sub-bab ini akan dikembangkan metode penyelesaian sistem persamaan
linear dengan menggunakan iterasi titik tetap, yaitu Iterasi Jacobi dan Iterasi Gauss
Seidel.
a. Iterasi Jacobi
Pada metode iterasi Jacobi, sistem persamaan linear dibentuk menjadi persamaa-persamaan
eksplisit, yang selajutnya dijadikan sebagai model iterasi. Nilai awal akan diberikan untuk menghitung nilai konstanta-konstanta tak diketahui pada iterasi pertama, begitu
seterusnya.
Pertimbangkan sistem persamaan linear berikut ini.
a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3
(3.22)
Persamaan (3.22) dapat ditulis dalam bentuk,
x =
y =
z =
1
(d1 − b1 y − c1 z)
a1
1
(b2 − a2 x − c2 z)
b2
1
(b1 − a3 x − b3 y)
c3
(3.23)
Secara persamaan-persamaan di atas dapat diubah ke dalam Iterasi Jacobi,
xi+1 =
yi+1 =
zi+1 =
Contoh 3.6
1
(d1 − b1 yi − c1 zi )
a1
1
(d2 − a2 xi − c2 zi )
b2
1
(d3 − a3 xi − b3 yi )
c3
(3.24)
54
Bab 3 Penyelesaian Sistem Linear
Selesaikan sistem persamaan berikut.
4x − y + z =
7
4x − 8y + z = −21
−21x + y + 5z =
15
(3.25)
dengan nilai awal (x0 , y0 , z0 ) = (1, 2, 2).
Penyelesaian:
Tulis persamaan di atas dalam bentuk,
x =
y =
z =
1
(7 + y − z)
4
1
(21 + 4x + z)
8
1
(15 + 2x − y)
5
Dan jika ditulis dalam bentuk iterasi Jacobi,
xi+1 =
yi+1 =
zi+1 =
1
(7 + yi − zi )
4
1
(21 + 4xi + zi )
8
1
(15 + 2xi − yi )
5
Selanjutnya, substitusikan x0 = 1, y0 = 2, z0 = 2 ke dalam persamaan iterasi Jacobi,
x1 =
y1 =
z1 =
1
(7 + 2 − 2) = 1, 75
4
1
(21 + 4+) = 3, 375
8
1
(15 + 2 − 2) = 3, 00
5
Jika kita lakukan langkah-langkah yang sama secara menerus, maka iterasi kelihatannya
konvergen sebagaimana yang ditunjukkan pada Tabel (3.1).
b. Iterasi Gauss-Seidel
Metode iterasi Gauss-Seidel yang digunakan untuk menentukan penyelesaian sistem
persamaan linear mempunyai prinsip kerja yang sama dengan metode iterasi jacobi,
tetapi iterasi yang dilakukan dengan menggunakan metode Gauss-Seidel lebih cepat
pada kasus-kasus penyelesaian yang konvergen.
Pada iterasi Gauss-Seidel, xi+1 digunakan untuk menggantikan xi pada perhitungan yi+1 , dan nilai-nilai xi+1 , yi+1 juga digunakan untuk menggantikan xi dan yi
pada perhitungan zi+1 .
3.4 Metode Iterasi untuk Sistem Linear
55
Tabel 3.1 Konvergensi Iterasi jacobi untuk sistem linear (5.4)
i
xi
yi
zi
0
1
2
3
4
..
.
1,0
1,75
1,84375
1,9625
1,99062500
..
.
2,0
3,375
3,875
3,925
3,97656250
..
.
2,0
3,0
3,025
2,9625
3,00000000
..
.
15
..
.
1,99999993
..
.
2,00000000
3,99999985
..
.
4,00000000
3,00093750
..
.
3,00000000
19
Sekarang, pandang kembali persamaan
a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3
(3.26)
Persamaan pada sistem (3.26) dapat diubah menjadi bentuk iterasi Gauss-Seidel, yaitu,
xi+1 =
yi+1 =
zi+1 =
1
(d1 − b1 yi − c1 zi )
a1
1
(d2 − a2 xi+1 − c2 zi )
b2
1
(d3 − a3 xi+1 − b3 yi+1 )
c3
(3.27)
Contoh 3.7
Pertimbangkan kembali persamaan pada contoh soal (5.4),
4x − y + z =
7
4x − 8y + z = −21
−21x + y + 5z =
15
dengan P0 = (x0 , y0 , z0 ) = (1, 2, 2).
Penyelesaian:
(3.28)
56
Bab 3 Penyelesaian Sistem Linear
Proses iterasi Gauss-Seidel yang diberikan adalah,
xi+1 =
yi+1 =
zi+1 =
1
(7 + yi − zi )
4
1
(21 + 4xi+1 + zi )
8
1
(15 + 2xi+1 − yi+1 )
5
Dengan mensubstitusikan y0 = 2 dan z0 = 2 diperoleh nilai x1 ,
x1 =
7+2−2
= 1, 75
4
dan substitusikan x1 = 1, 75 dan z0 = 2 kedalam persamaan kedua, dan diperoleh,
1
y1 = [15 + 2(1, 75) − 3, 75] = 3, 75
8
Selanjutnya, substitusikann x1 = 1, 75 dan y1 = 3, 75 ke dalam persamaan ketiga dan
diperoleh,
1
z1 = (15 + 291, 75) − 3, 75) = 2, 95
5
Dari iterasi pertama diperoleh P1 = (x1 , y1 , z1 ) = (1, 75; 3, 75; 2, 95)
Dari hasil perhitungan terlihat bahwa P1 lebih dekat ke nilai sebenarnya (2, 4, 3)
dibandingkan dengan P0 dan lebih baik dibandingan dengan iterasi jacobi.
Jika barisan terus-menerus dilakukan iterasi, terlihat hasil yang konvergen ke
(2, 4, 3) sebagaimana terlihat pada Tabel (3.2).
Latihan
3.3
1. Gunakan iterasi Jacobi dan Iterasi Gauss-Seidel untuk menentukan Pi (i = 1, 2, 3)
dengan P0 = (x0 , y0 , z0 ) = (0, 0, 0) untuk sistem linear berikut. Apakah jacobi
dan Gauss-seidel konvergensi ke penyelesaian yang dimaksud?
(a)
4x − y = 15
x + 5y = 9
(b)
8x − 3y = 10
−x + 4y = 6
(c)
−x + 3y = 1
6x − 2y = 2
(d)
2x + 3y = 1
7x − 2y = 1
3.4 Metode Iterasi untuk Sistem Linear
57
Tabel 3.2 Konvergensi Iterasi Gauss-Seidel untuk sistem linear (3.28)
i
xi
yi
zi
0
1
2
3
..
.
1,0
1,75
1,95
1,995625
..
.
2,0
3,375
3,96875
3,996099375
..
.
2,0
2,950
2,98625
2,99903125
..
.
1,99999983
1,99999998
2,00000000
3,99999988
3,99999999
4,00000000
2,99999996
3,00000000
3,00000000
8
9
10
2. Gunakan iterasi Jacobi dan Iterasi Gauss-Seidel untuk menentukan Pi (i = 1, 2, 3)
dengan P0 = (x0 , y0 , z0 ) = (0, 0, 0) untuk sistem linear berikut. Apakah jacobi
dan Gauss-seidel konvergensi ke penyelesaian yang dimaksud?
5x − y + z = 10
2x + 8y − z = 11
−x + y + 4z = 3
(b)
2x + 8y − z = 11
5x − y + z = 10
−x + y + 4z = 3
x − 5y − z = −8
(c) 4x + y − z = 13
2x − y − 6z = −2
(d)
4x + y − z = 13
x − 5y − z = −8
2x − y − 6z = −2
(a)
3. Pertimbangkan sistem linear berikut.
5x + 3y = 6
4x − 2y = 8
Dapatkanh, baik metode iterasi jacobi maupun Gauss-Seidel dapat menentukan
penyelesaian dari persamaan linear di atas?
4. Dapatkah iterasi Jacobi digunakan untuk menyelesaian sistem persamaan linear
berikut.
2x + y − 5z = 9
x − 5y − z = 14
7x − y − 3z = 26
58
Bab 3 Penyelesaian Sistem Linear
5. Pertimbangkan sistem linear triagonal berikut ini dan asumsikan bahwa matriks
koefisien adalah matriks diagonal.
d1 x1 + c1 x2
a1 x1 + d2 x2
a2 x2
+
+
..
.
c2 x3
d3 x3
an−2 xn−2
+
c3 x4
..
.
+ dn−1 xn−1
an−1 xn−1
=
=
=
..
b1
b2
b3
..
.
.
+ cn−1 xn = bn−1
+
dn xn = bn
Tulislah algoritma yang dapat digunakan untuk menyelesaikan persoalan tersebut.
BAB 4
AKAR-AKAR PERSAMAAN NONLINEAR
Pada persoalan matematika, kita sering ditemukan masalah di dalam menentukan akar
dari suatu persamaan yang berbentuk
f (x) = 0
(4.1)
Penyelesaian suatu persamaan pada dasarnya adalah nilai-nilai variabel bebas yang
membuat nilai fungsi menjadi nol. Jika α adalah suatu akar persamaan dari fungsi f (x),
maka f (α) = 0. Pada kasus ini, fungsi f (x) adalah tak linear yang dapat berbentuk:
1. Persamaan aljabar
Persamaan aljabar biasanya berbentuk polinom,
an xn + an−1 xn−1 + · · · + a2 x2 + aa x + a0 = 0
dengan an = 0, n ≥ 2
2. Persamaan Transenden
Persamaan transenden adalah persamaan yang melibatkan fungsi-fungsi trigonometri,
eksponen dan logaritma, misalnya
e2x−3 − 4 sin(3x2 + 2) = 0
ln(x + 2) − 3 = 0
log(3x − 2) + cos(x + 1) = 0
3. Persamaan campuran
Persamaan yang melibatkan persamaan aljabar dan persamaan transenden
x2 cos(x + 1) − 3x6 = 0
60
Bab 4 Akar-Akar Persamaan Nonlinear
x3 e + ex (x−3 ) = 0
e2x
2 −1
x4 − tan(x − 4) = 0
Untuk menentukan penyelesaian suatu persamaan, banyak cara dilakukan. Beberapa teknik telah digunakan, misalnya dengan menggunakan grafik atau memebuat
tabulasi atau kedua-duanya digunakan secara bersama-sama.
Pada kenyataanya, banyak persamaan non linear yang cukup sulit untuk menentukan solusinya. Hal ini terjadi ketika tidak terdapat rumusan untuk menentukan solusi
secara analisis. Untuk itu, kita gunakan metode pendekatan dengan melibatkan iterasi
(yang secara umum pendekatan terbaik akan digunakan) untuk menentukan solusi persamaan non linear.
Misalkan diberikan suatu fungsi
f (x) = 0
(4.2)
dan s dikatakan solusi dari persamaan (4.2) jika
f (s) = 0
(4.3)
atau secara geomteri dapat ditentukan nilai s sebagai solusi dari f (x), dengan menentukan absis perpotongan sumbu-X dengan kurva f (x).
Pada sub-bab ini, akan diberikan suatu pendekatan untuk menentukan solusi
persamaan nolinear.
4.1
Metode Bagidua
Misalkan f adalah fungsi kontinu terdefinisi pada interval [a, b] dengan f (a) dan
f (b) saling berlawanan tanda sebagaimana ditunjukkan pada Gambar 4.1.
Dengan menggunakan teorema Kalkulus lanjut, terdapat α di dalam (a, b) dengan f (α) = 0. Misalkan kita ambil interval [a, b] dan α terletak di dalamnya sehingga
f (a)f (b) < 0. Pada setiap kali iterasi, interval [a, b] dibagi dua di x = c dengan
c = (a + b)/2 sehingga terdapat dua sub-interval, yaitu [a, c] dan [c, b]. Selang yang
diambil untuk iterasi adalah selang yang memuat akar α yang memenuhi f (a)f (c) < 0
atau f (b)f (c) < 0.
Selang yang baru lagi dibagi dua dengan cara yang sama. Begitu seterusnya
sampai ukuran selang baru menjadi sangat kecil. Iterasi akan dihentikan jika memenuhi
4.1 Metode Bagidua
61
Y
f (x)
a
c
•
α
b
X
Gambar 4.1 Skematik metode Bagidua pada kurva y = f (x) yang memotong
sumbu x di α.
kondisi sebagai berikut.
1. Lebar interval baru lebih kecil dari nilai toleransi lebar interval yang diberikan,
|a − b| < ε.
2. Nilai fungsi hampiran di f (c) = 0
3. Galat relatif hampiran akar |(cn+1 − cn )/cn+1 | < δ, yang mana δ adalah galat
relatif yang diinginkan dan n = 0, 1, 2, · · ·
Metode Bagidua secara konsep sudah cukup jelas, tetapi konvergensi sangat lamban
(membutuhkan banyak iterasi N untuk menghasilkan galat, |p − pn |, yang cukup kecil).
Algoritma untuk menentukan akar persamaan diberikan sebagai berikut.
INPUT titik ujung a,b; toleransi TOL, jumlah iterasi N
OUTPUT akar pendekatan
Algoritma
1. set i=1
2. while i<=N do 3-6
3. def alpha := (a+b)/2
4. if f(alpha) = 0 atau |b-a| < TOL , maka
c adalah akar persamaan dan berhenti.
5. set i = i + 1
6. jika f(b)f(c) < 0 , maka a:=c ,
selain itu,
7. b:=c , kembali ke 2
62
Bab 4 Akar-Akar Persamaan Nonlinear
Teorema 4.1
Jika f ∈ [a, b] dan andaikan f (a) · f (b) < 0, metode Bagidua dapat digeneralisasi
terhadap barisan {pn } yang menghampiri p dengan kriteria-kriteria berikut,
|pn − p| ≤
b−a
,
2n
n≥1
Contoh 4.1
Tentukan akar persamaan
(x) = ex − 5x2
di dalam interval [0, 1] dan ε = 0, 001.
Penyelesaian:
Dengan menggunakan menggunakan algoritma metode Bagidua, diperoleh nilai-nilai
yang ditunjukkan pada tabel berikut.
Contoh 4.2
Tentukan akar-akar pendekatan dari
f (x) = x6 − x − 1 = 0
pada interval [1, 2].
Penyelesaian:
Dengan menggunakan algoritma Bagidua, diperoleh tabel sebagai berikut.
Contoh 4.3
Hitunglah banyaknya iterasi yang dibutuhkan untuk menyelesaikan
f (x) = x3 + 4x − 10 = 0
dengan akurasi = 10−3 , gunakan a1 = 1 dan b1 = 2
Penyelesaian:
4.1 Metode Bagidua
63
Tabel 4.1 Hasil hampiran metode bagidua untuk f (x) = ex − 5x2 dengan
toleransi ε = 0, 001
i
a
c
b
f (a)
f (c)
f (b)
selang
lebar
0
1
2
3
4
5
6
7
8
9
10
0,0000
0,5000
0,5000
0,5000
0,5625
0,5938
0,5938
0,6016
0,6016
0,6016
0,6045
0,5000
0,7500
0,6250
0,5625
0,5937
0,6094
0,6016
0,6055
0,6035
0,6045
0,6050
1,0000
1,0000
0,7500
0,6250
0,6250
0,6250
0,6094
0,6094
0,6055
0,6055
0,6055
1,0000
0,3987
0,3987
0,3987
0,1730
0,4081
0,4081
0,0156
0,0156
0,0074
0,0033
0,3987
-0,6955
-0,6955
0,1730
0,0481
0,0175
0,0156
-0,0009
0,0074
0,0033
0,0012
-2,2817
-2,2817
-0,6955
-0,0849
-0,0849
-0,0849
-0,0174
-0,0174
-0,0009
-0,0009
-0,0009
[c,b]
[a,c]
[a,c]
[c,b]
[c,b]
[a,c]
[c,b]
[a,c]
[c,b]
[c,b]
[c,b]
0,5000
0,2500
0,1250
0,0625
0,0313
0,0156
0,0078
0,0039
0,0020
0,0010
0,0005
Tabel 4.2 Hasil hampiran metode bagidua untuk f (x) = x6 −x−1 = 0 dengan
toleransi ε = 0, 001
i
1
2
3
4
5
6
7
8
9
10
a
b
c
1,0000
1,0000
1,0000
1,1250
1,1250
1,1250
1,1250
1,1328
1,1328
1,1328
2,0000
1,5000
1,2500
1,2500
1,1875
1,1562
1,1406
1,1406
1,1367
1,1348
1,5000
1,2500
1,1250
1,1875
1,1562
1,1406
1,1328
1,1367
1,1348
1,1338
b−c
0,5000
0,2500
0,1250
0,0625
0,0312
0,0156
0,0078
0,0039
0,0020
0,00098
f (α)
8,8906
1,5647
-0,0977
0,6167
0,2333
0,0616
-0.0196
0,0206
0,0004
-0,0096
Metode Bagidua akan menghasilkan akar-akar persamaan jika |p − pn | ≤ . Dari soal
64
Bab 4 Akar-Akar Persamaan Nonlinear
ditentukan bahwa = 10−3 . Oleh karena itu,
|pn − p| ≤
b1 − a1
(2 − 1)
=
< 10−3
n
2
2n
dengan menggunakan logaritma,
log(2−n ) < log(10−3 )
−n log(2) < −3
3
n>
≈ 9, 96
log(2)
Kasus yang Mungkin Terjadi
1. Jumlah akar lebih dari satu
Bila dalam selang [a, b] terdapat lebih dari satu akar (banyaknya akar ganjil)
sebagaimana ditunjukkan pada Gambar 4.2.
Y 6
a
b-
X
Gambar 4.2 Kurva y = f (x) yang mempunyai akar berjumlah ganjil.
2. Akar ganda
Untuk beberapa fungsi yang mempunyai akar kembar atau imajiner, metode bagi
dua tidak dapat menemukan aka-akar polinom.Hal ini disebabkan karena tidak
terdapat perbedaan tanda pada ujung-ujung selang yang baru, sebagaimana ditunjukkan pada Gambar 4.3(a) dan Gambar 4.3(b).
3. Singularitas
Pada suatu fungsi f (x), kadang kala terdapat nilai yang tidak terdefinisi pada x
4.1 Metode Bagidua
65
Y 6
Y 6
a
b -X
a
(a) Polinom yang tidak mempunyai
akar
b -X
(b) Polinom yang mempunyai akar
kembar
Gambar 4.3 Polinom yang mempunyai akar ganda
tertentu. Jika selang [a, b] memuat titik singular, maka iterasi metode bagidua
tidak pernah berhenti. Hal ini disebabkan karena metode bagidua menganggap
titik singular sebagai akar polinom.
Y 6
a
b
X
-
Gambar 4.4 Interval [a, b] yang memuat titik singular kurva y = f (x)
Batas galat yang diperoleh dari metode biseksi (bagi dua) adalah sebagai berikut.
Misalkan an , bn dan cn masing-masing melambangkan nilai-nilai ke-n yang dihitung dari a, b dan c. Untuk itu, diperoleh
1
bn+1 − an+1 = (bn − an ),
2
n≥1
dan
bn − an =
1
2n−1
(b − a),
n≥1
(4.4)
66
Bab 4 Akar-Akar Persamaan Nonlinear
dimana b − a menujukkan panjang interval awal kita mulai. Oleh karena itu, akar-akar
persamaan berada pada interval [an , cn ] atau [cn , bn ], maka
1
|α − cn | ≤ cn − an = bn − cn = (bn − an )
2
(4.5)
Batas galat untuk cn diperoleh dari kombinasi persamaan 4.4,
|α − cn | ≤
1
(b − a)
2n
(4.6)
Persamaan 4.6 menunjukkan iterasi cn yang konvergen menuju α apabila n → ∞
Untuk membatasi banyaknya iterasi (n) yang akan dilakukan dalam perhitungan, maka kita butuhkan suatu nilai ε sebagai batas dari galat,
|α − cn | ≤ ε
sehingga
1
(b − a) ≤ ε
2n
atau
b−a
ε
2n ≥
Dengan menggunakan logaritma pada kedua sisi diperoleh,
n≥
ln
b−a
ε
(4.7)
ln 2
Latihan
4.1
1. Gunakan metode Bagidua untuk menentukan penyelesaian fungsi f (x) = x3 −
7x2 + 14x − 6 = 0 dengan akurasi 10−2 pada interval:
a. [0, 1]
b. [1; 3, 2]
c.[3, 2; 4]
2. Gunakan metode Bagidua untuk menentukan penyelesaian fungsi f (x) = x4 −
2x3 − 4x2 + 4x + 4 = 0 dengan akurasi 10−2 pada interval:
a. [−2, −1]
b.[0, 2]
c.[2, 3]
d. [−1, 0]
3. Gunakakan metode Bagidua untuk menentukan penyelesaian f (x) = tan(x) − x =
0 dengan akurasi 10−3 pada interval [4; 4, 5]
4.2 Metode Newton-Raphson
67
4. Gunakakan metode Bagidua untuk menentukan penyelesaian f (x) = 2 + cos(ex −
2) − ex = 0 dengan akurasi 10−3 pada interval [0, 5; 1, 5]
5. Gunakakan metode Bagidua untuk menentukan penyelesaian fungsi-fungsi berikut
dengan akurasi 10−3 .
a. x − 2−x = 0,
0 ≤ x ≤ 1,
b. ex − x2 + 3x − 2 = 0,
0≤x≤1
c. 2x cos(2x) − (x + 1)2 = 0
− 3 ≤ x ≤ −2,
d. x cos(x) − 2x2 + 3x − 1 = 0
6. Tentukan hampiran terhadap
√
3
0, 2 ≤ x ≤ 0, 3
−1 ≤ x ≤ 0
1, 2 ≤ x ≤ 1, 3
25 dengan keakurasian 10−4 dengan menggunakan
metode Bagidua. (petunjuk: pertimbangkan f (x) = x3 − 25).
7. Tentukan hampiran
√
3 dengan akurasi 10−4 dengan menggunakan metode Bagidua.
8. Dengan menggunakan teorema, tentukan batas iterasi yang dibutuhkan untuk
menghampiri penyelesaian x3 − x − 1 = 0 denagn ketelitian 10−4 pada interval
[1, 4].
9. Dengan menggunakan teorema, tentukan batas iterasi yang dibutuhkan untuk
menghampiri penyelesaian x3 + x − 4 = 0 denagn ketelitian 10−4 pada interval
[1, 2].
10. Misalkan {pn } adalah suatu barisan yang didefinisikan pn =
bahwa lim (pn − pn−1 ) = 0, tetapi {pn } divergen.
n
1
k=1
k
. Tunjukkan
n→∞
4.2
Metode Newton-Raphson
Metode Newton-Raphson
1
adalah metode yang paling terkenal dan paling
banyak digunakan dalam bidang sains dan rekayasa. Hal ini karena metode NewtonRaphson konvergensinya paling cepat.
1
Beberapa buku menyebutnya metode Newton. Joseph Raphson (1648-1715) adalah matematikawan
Inggris yang mempublikasikan metode Newton
68
Bab 4 Akar-Akar Persamaan Nonlinear
Y
(x0 , f (x0 ))
f (x)
(x1 , f (x1 ))
O
α•
X
x2
x0
x1
Gambar 4.5 Skematik metode Newton-Raphson pada kurva y = f (x) yang
memotong sumbu x di α.
Pertimbangkan fungsi y = f (x) yang memotong sumbu-x di α dan sebuah garis
lurus memotong sumbu-x di x1 dan menyinggung y = f (x) titik (x0 , f (x0 )), maka
kemiringan garis tersebut dapat dihitung,
m=
f (x0 ) − 0
x0 − x1
Titik singgung kurva y = f (x) pada x = x0 adalah kemiringan m, sehingga dapat
ditulis,
f (x) =
f (x0 ) − 0
x0 − x1
atau
x1 = x0 −
f (x0 )
f (x0 )
(4.8)
Oleh karena x1 terletak di antara x0 dan α (akar-akar persamaan), artinya x1 lebih
dekat ke akar persamaan, maka selanjutnya kita tentukan derivatif y = f (x) di x = x1 .
Kemiringan garis yang menyinggung y = f (x), juga memotong sumbu-x di x2 , maka
derivatif untuk y = f (x) di x = x1 , ditulis,
f (x) =
f (x1 − 0
x1 − x2
atau
x2 = x1 −
f (x1 )
f (x1 )
(4.9)
4.2 Metode Newton-Raphson
69
dan
f (x2 )
f (x2 )
x3 = x2 −
(4.10)
Pengulangan proses ini akan memperoleh barisan x1 , x2 , x3 , . . ., yang akan menghampiri
akar persamaan α. Oleh karena itu, secara umum rumus penghampiran metode NewtonRaphson ditulis,
xn+1 = xn −
f (xn )
,
f (xn )
n = 0, 1, 2, . . .
(4.11)
Pengulangan proses hampiran tersebut akan berhenti jika memenuhi kondisi sebagai
berikut.
1. |xn+1 − xn | < ε, yang mana ε adalah nilai toleransi yang diberikan
x
n+1 − xn 2. < δ dengan δ adalah galat relatif yang diinginkan
xn+1 Selain dengan menggunakan tafsiran geomteri, penurunan rumusan Newton juga dapat
dilakukan dengan menggunakan interpolasi polinomial Taylor. Pertimbangkan sebuah
deret Taylor orde satu untuk f (x) yang diekspan disekitar x0 sebagai berikut.
f (x) = f (x0 ) + (x − x0 )f (x0 ) +
1
(x − x0 )2 f (ξ(x))
2!
(4.12)
di mana ξ(x) terletak di antara x dan x0 . Oleh karena α adalah akar-akar persamaan
f (x) yang akan ditentukan maka f (α) = 0, sehingga x = α.
Selanjutnya gantikan x dengan α pada polinomial Taylor akan memberikan
f (α) = f (x0 ) + (α − x0 )f (x0 ) +
1
(α − x0 )2 f (ξ(α))
2!
(4.13)
Pada metode Newton di asumsikan bahwa galat mutlak |α − x0 | sangat kecil, sehingga
bentuk (α − x0 )2 diabaikan (karena nilainya yang sangat kecil) dan dengan memotong
deret Taylor sampai orde satu akan diperoleh,
f (α) ≈ f (x0 ) + (α − x0 )f (x0 )
0 ≈ f (x0 ) + (α − x0 )f (x0 )
dan penyelesaian untuk α diberikan oleh
α ≈ x0 −
f (x0 )
f (x0 )
(4.14)
70
Bab 4 Akar-Akar Persamaan Nonlinear
Jika kita generalisai dengan mengasumsikan bahwa penyelesaian tersebut merupakan
suatu deret xn dengan x0 sebagai nilai pendekatan awal, maka bentuk ungkapan pada
persamaan (4.14) dapat ditulis secara umum,
f (xn )
, n = 0, 1, 2, . . .
f (xn )
Teorema 4.2 Algoritma Newton-Raphson
xn+1 = xn −
(4.15)
Untuk menentukan akar f (x) = 0, diberikan dua nilai x0 dan dengan menggunakan
iterasi
xn+1 = xn −
f (xn )
f (xn )
Algoritma metode Newton adalah sebagai berikut.
INPUT nilai awal x0, toleransi tol
OUTPUT akar persamaan
Algoritma
1. repeat x_lama <--x
x:=x-f(x)/f_aksen(x)
kembali ke 2
2. | x-x_lama| < tol
3. tulis akar x
Secara umum, metode Newton-Raphson kekonverenannya sangat cepat, seperti
ditunjukkan pada Gambar 4.5. Namun, karena metode Newton-Raphson termasuk
pada kelompok metode terbuka, maka dalam beberapa kasus, iterasinya justru menjadi
divergen. Hal ini biasa terjadi jika tidak tepat dalam menentukan titik awal (x0 ), seperti
yang ditunjukkan pada Gambar 4.6.
Untuk kasus di atas, menentukan titik awal harus tepat. Salah dalam menentukan titik awal akan mengakibatkan iterasi menjadi divergen. Pemilihan titik awal
sebaiknya dekat dengan akar-akar persamaan. Untuk itu, membuat sketsa grafik akan
sangat membantuk sekali dalam menentukan titik awal.
Pada kasus persamaan nonlinear yang tidak mempunyai akar, iterasi yang terjadi akan divergen berisolasi.
Analisis Galat
4.2 Metode Newton-Raphson
Y 6
71
TT
T
T
T
T
T
T
T
X
T
x0
x2 x3T x1
Gambar 4.6 Konvergensi yang terjadi pada metode Newton
Asumsikan bahwa f (x) mempunyai turunan kedua untuk semua nilai x pada
interval yang memuat akar-akar persamaan α. Berdasarkan teorema Taylor, dapat kita
tuliskan
1
f (α) = f (xn ) + (α − xn )f (xn ) + (α − xn )2 f (ξn )
2
dengan ξn adalah titik sebarang diantara α dan xn . Dengan mengasumsikan bahwa
f (α) = 0 dan membaginya dengan f (xn ) kita peroleh,
0=
f (xn )
2 f (ξn )
+
(α
−
x
)
+
(α
−
x
)
n
n
f (xn )
2f (xn )
(4.16)
Dari persamaan 4.11, suku pertama pada ruas kanan adalah xn − xn+1 , dan kita punyai
0 = xn − xn+1 + (α − xn ) + (α − xn )2
f (ξn )
2f (xn )
(4.17)
dan penyelesaian untuk α − xn+1 adalah
α − x+1 =
−f (ξn )
(α − xn )2
2f (xn )
(4.18)
Rumusan pada persamaan di atas menyebutkan bahwa galat pada iterasi xn+1 adalah
sebanding dengan kuadrat galat pada xn . Ketika galat awal cukup kecil, maka hal
ini menunjukkan galat akan terus menurun secara cepat. Persamaan 4.18 juga dapat
digunakan untuk memberikan pembuktikan matematis secara formal dari konvergensi
metode Newton.
72
Bab 4 Akar-Akar Persamaan Nonlinear
Contoh 4.4
Tentukan nilai akar persamaan f (x) = x6 − x − 1
Penyelesaian:
f (x) = x6 − x − 1, maka turunannya adalah f (x) = 6xx − 1 dan iterasinya adalah,
xn+1 = xn −
x6n − xn − 1
6x5n − 1
Andaikan digunakan nilai tebakan awal, x0 = 1, 5, dan toleransi ε = 0, 000001, maka
akan diperoleh nilai-nilai xn untuk n = 0, 1, . . . , 6 yang diberikan pada tabel berikut.
Tabel 4.3 Perhitungan akar persamaan f (x) = x6 − x − 1 dengan nilai awal
x0 = 1, 5
n
xn
f (xn )
0
1
2
3
4
5
6
1,5
1,30049088
1,18148042
1,13945559
1,13477763
1,13472415
1,13472414
8,89E+1
2, 54E + 1
5, 38E − 1
4, 92E − 2
5, 50E − 4
6, 80E − 8
−4, 00E − 9
xn − xn−1
−2, 00E − 1
−1, 19E − 1
−4, 20E − 2
−4, 68E − 3
−5, 35E − 5
−1, 00E − 8
Contoh 4.5
Tentukan nilai akar persamaan f (x) = ex − 5x2
Penyelesaian:
f (x) = ex − 5x2 , maka turunannya adalah f (x) = ex − 10x dan iterasinya adalah,
xn+1 = xn −
exn − 5xn
exn − 10xn
Andaikan digunakan nilai tebakan awal, x0 = 1, 5, dan toleransi ε = 0, 001, maka akan
diperoleh nilai-nilai xn untuk n = 0, 1, . . . , 3 yang diberikan pada tabel berikut. Contoh
di atas memperlihatkan bahwa metode Newton-Raphson memerlukan hanya sedikit iterasi dibandingkan dengan metode bagidua.
4.2 Metode Newton-Raphson
73
Tabel 4.4 Perhitungan akar persamaan f (x) = ex − 5x2 dengan nilai awal
x0 = 1
|xn − xn−1 |
n
xn
0
1
2
3
0,500000
0,618976
0,605444
0,605267
–
0,118976
0,013532
0,000177
Contoh 4.6
Buatlah rumusan iterasi Newton untuk menghitung akar kuadrat x dari bilangan positif
c dan gunakan untuk c = 2
Penyelesaian:
Dari soal kita punya x =
√
c, maka f (x) = x2 − c = 0 dan f (x) = 2x. Dengan
menggunakan rumusan metode Newton diperoleh,
x2n − c
2xn
2
1 xn + c
2
xn
1
c
xn +
2
xn
xn+1 = xn −
=
=
(4.19)
Jika kita masukan nilai c = 2 ke dalam persamaan (4.19), maka akan diperoleh nilainilai,
x= 1, 500000
x2 = 1, 416667
x3 = 1, 414216
Contoh 4.7
Gunakan metode Newton pada persamaan
f (x) = x3 + x − 1 = 0
x4 = 1, 414214
74
Bab 4 Akar-Akar Persamaan Nonlinear
dengan nilai awal x0 = 1
Penyelesaian:
Jika f (x) = x3 + x − 1 = 0, maka f (x) = 3x2 + 1, sehingga dengan menggunakan
rumusan Newton diperoleh,
x3n + xn − 1
3x2n + 1
2
xn (3xn + 1) x3n + xn − 1
−
3x2n + 1
3x2n + 1
2x3n + 1
, n = 0, 1, 2, . . .
3x2n + 1
xn+1 = xn −
=
=
(4.20)
Untuk nilai awal x0 = 1, maka akan memberikan,
x1 = 0, 750000,
x2 = 0, 686047,
x3 = 0, 682340,
x4 = 0, 682328
Modifikasi Metode Newton-Raphson
Pada pembahasan terdahulu telah diberikan bahwa untuk kasus akar ganda,
metode bagidua dan metode tertutup lainnya tidak berhasil menemukan karena f (a)f (b)
bernilai positif. Metode terbuka, seperti metode Newton-Raphson dapat diterapkan
pada kasus seperti ini.
Dalam menentukan hasil pada polinom akar-akar ganda, kecepatan konvergensi
metode Newton-Raphson tidak lagi kuadratis, tetapi berjalan secara linear. Untuk itu,
diberikan alternatif dengan memisalkan
u(x) =
f (x)
f (x)
dan
u (x) =
=
=
f (x) f (x)
f (x)f (x) − f (x)f (x)
[f (x)]2
2
[f (x)] − f (x)f (x)
[f (x)]2
Oleh karena
xi+1 = xi −
u(xi )
u (xi )
(4.21)
4.2 Metode Newton-Raphson
75
maka,
x1+i = xi −
f (xi )/f (xi )
([f (xi )]2 − f (xi )f (xr ))/([f (xi )]2 )
atau
xi+1 = xi −
f (xi )f (xi )
[f (xi )]2 − f (xi )f (xi )
(4.22)
Contoh 4.8
Hitunglah akar dari
f (x) = x3 − 5x2 + 7x − 3
dengan menggunakan metode Newton-Raphson baku dan Newton-Rapshon modifikasi,
dengan tebakan awal x0 = 0.
Penyelesaian:
Jika
f (x) = x3 − 5x2 + 7x − 3,
maka
f (x) = 3x2 − 10x + 7
dan f (x) = 6x − 10.
Dengan menggunakan rumus Newton-Raphson diperoleh,
xi+1 = xi −
x3i − 5x2i + 7xi − 3
3x2 − 10xi + 7
dan untuk metode Newton-Raphson dimodifikasi diperoleh,
xi+1 = xi −
3
xi − 5x2i + 7xi − 3 3x2 − 10xi + 7
(3x2 − 10xi + 7)2 − (6xi − 10)(x3i − 5x2i + 7xi − 3)
Hasil perhitungan dari metode Newton-Rapshon baku dan Newton-Raphson modifikasi
diberikan pada Tabel 4.5.
Dari Kedua metode, ternyata konvergensi iterasi menuju ke x = 1. Namun terlihat
perbedaan pada jumlah iterasi yang dilakukan, yang mana metode Newton-Raphson
modifikasi dua lebih cepat konvergensinya dibandingkan dengan metode Newton-Raphson
baku.
Namun tidak semua persoalan menunjukkan bahwa metode Newton-Raphson
yang dimodifikasi lebih cepat konvergensinya di bandingkan dengan metode NewtonRaphson. Contoh berikut akan memberikan pemahaman tentang hal tersebut lebih
mendalam.
76
Bab 4 Akar-Akar Persamaan Nonlinear
Tabel 4.5 Perbadingan kecepatan konvergensi Newton-Raphson baku dan
modifikasi pada kasus f (x) = x3 − 5x2 + 7x − 3 dengan nilai awal
x0 = 0
n
0
1
2
3
4
5
6
xn (baku)
0,000000000
0,428571429
0,685714286
0,832865400
0,913328983
0,955783293
0,977655101
xn (modifikasi)
000000000
1,105263158
1,003081664
1,000002382
Contoh 4.9
Selesaikan fungsi berikut ini
f (x) = x3 + 4x2 − 10 = 0
dan selanjutnya bandingkan hasil akar-akarnya dengan menggunakan metode NewtonRaphson dan metode Newton-Raphson yang dimodifikasi, jika salah satu akarnya adalah
x = 1, 36523001.
Penyelesaian:
Dari soal,
f (x) = x3 + 4x2 − 10,
maka
f (x) = 3x2 + 8x dan f (x) = 6x + 8,
sehingga rumusan untuk metode Newton-Rapson adalah
(i)
xn = xn−1 −
x3n−1 + 4x2n−1 − 10
,
3x2n−1 + 8xn−1
dan rumusan untuk metode Newton-Raphson dimodifikasi,
(ii)
xn = xn−1 −
(x3n−1 + 4x2n−1 − 10)(3x2n−1 + 8xn−1 )
(3x2n−1 + 8xn−1 )2 − (x3n−1 + 4x2n−1 − 10)(6xn−1 + 8)
4.2 Metode Newton-Raphson
77
Untuk nilai awal x0 = 1, 5, tiga iterasi pertama menunjukkan konvergensi yang cukup
cepat sebagaimana ditunjukkan pada Tabel 4.6.
Tabel 4.6 Perbadingan kecepatan konvergensi Newton-Raphson baku dan
modifikasi pada kasus f (x) = x3 + 4x2 − 10 dengan nilai awal
x0 = 1, 5
xi
1
2
3
xn−1
1,37333333
1,36526201
1,36523001
xn
1,35689898
1,36519585
1,36523001
Latihan
4.2
1. Tentukan akar-akar persamaan berikut.
a. x + cos x = 0
b. e−x + sin x − 2 = 0
c. 1 − x − e−2x = 0
d. 2x + tan x = 0
e. 2x2 − e−x = 0
2. Carilah akar-akar persamaan x5 = x + 0, 2 dengan metransformasikan persamaan
tersebut ke bentuk xn+1 = g(xn ) dengan mengambil nilai awal x0 = 0
3. Pada persoalan no. 2, jika bentuk persamaan tersebut ditulis dalam bentuk x =
√
5
x + 0, 2 dan melakukan iterasi dengan mengambil nilai tebakan awal x = 1,
tentukan akas-akar persamaan.
4. Apa yang terjadi, jika pada soal no.2 transformasi yang dibuat adalah x = x5 −0, 2
dengan nilai awal x0 = 1
5. Gunakan metode Newton dari fungsi-fungsi berikut dengan akurasi 6 (enam) digit
a. sin x = cot x,
x0 = 1
78
Bab 4 Akar-Akar Persamaan Nonlinear
b. x = cos x,
x0 = 1
c. x3 − 5x + 3 = 0,
d. x + ln x = 2,
x0 = 2
x0 = 2
6. Buatlah iterasi Newton untuk akar pangkat tiga dan kemudian hitung
√
3
7 dengan
mengambil nilai awal x0 = 2 dan keakurasian enam digit.
√
7. Buatlah rumusan iterasi Newton untuk k c, (c > 0) dan gunakan rumusan terse√ √ √ √
but untuk menghitung 2, 3 2, 4 2, 5 2 dengan mengambil nila awal x0 = 1 dan
keakurasian enam digit.
8. Gunakan Metode Newton dengan keakurasisn 10−4 untuk menyelesaikan persoalanpersoalan berikut.
a. x3 − 2x2 − 5 = 0, [1, 4]
b. x3 + 3x2 − 1 = 0, [−3, −2]
c. x − cos x = 0, [0, π/2]
d. x − 0, 8 − 0, 2 sin x = 0, [0, π/2]
9. Gunakan metode Newton pada persamaan-persamaan berikut dengan nilai awal
x0 yang telah diberikan dan lakukan 3 langkah.
a. x3 − 5x + 3 = 0,
b.
x4
−
x3
x0 = 2
− 2x − 34 = 0,
x0 = 3
c. x3 − 3, 9x2 + 4, 79x − 1, 881 = 0,
d. sin x = cot x,
x0 = 1 e.
e−x
x0 = 1
= tan x,
x0 = 1
10. Tunjukkan bahwa soal no. 9(a) dapat diubah dalam bentu x = (x3 + 3)/5. Selesaikan dengan menggunakan iterasi sebanyak 4 langkah dan nilai awal x0 = 1.
11. Gunakan metode Newton dengan akurasi 10−5 untuk menyelesaikan masalahmasalah berikut.
a. ex + 2−x + 2 cos x − 6 = 0,
1≤x≤2
b. ln(x − 1) + cos(x − 1) = 0,
1, 2 ≤ x ≤ 2
c. x2 − 2xe−x + e−2x = 0, 0 ≤ x ≤ 1
√
√
d. cos(x + 2) + x(x/2 + 2) = 0, −2 ≤ x ≤ −1
e. x3 − 3x2 (2−x ) = 3x(4−x ) − 8−x = 0,
0≤x≤1
4.3 Metode Secant
79
f. e6x + 3(ln 2)2 e2x − e4x ln 8 − (ln 2)3 = 0,
g. (x − 2)2 − ln x = 0,
h. ex − 3x2 = 0,
i. sin x −
e−x
0≤x≤1
1 ≤ x ≤ 2, 3 ≤ x ≤ 4
0 ≤ x ≤ 13 ≤ x ≤ 5
0 ≤ x ≤ 1, 3 ≤ x ≤ 4, 6 ≤ x ≤ 7
= 0,
12. Gunakan metode Newton dengan akurasi 10−5 untuk menyelesaikan persoalan
berikut.
1 1 2
1
+ x − x sin x − cos 2x,
2 4
2
0=
x0 =
π
2
Jelaskan apa yang terjadi pada hasil iterasi tersebut, dan cobakan untuk x0 = 5π
dan x0 = 10π
13. Persamaan x2 −10 cos x = 0 mempunyai dua penyelesaian 1, 3793646 dan −1, 3793646.
Gunakan metode Newton untuk mendekati penyelesaian tersebut pada akurasi
10−5 dengan nilai awal:
4.3
a. x0 = 100
b. x0 = 50
c. x0 = −25
d. x0 = 25
e. x0 = 50
f. x0 = −100
Metode Secant
Misalkan fungsi y = f (x) memotong sumbu-x di α dan sebuah garis memotong
kurva y = f (x) di x1 dan x0 seperti yang ditunjukkan pada Gambar 4.7.
Y
f (x)
x1
x2
x3
•
α
x0
X
Gambar 4.7 Skematik metode Secant pada kurva y = f (x) yang memotong
sumbu x di α.
80
Bab 4 Akar-Akar Persamaan Nonlinear
Nilai x2 ditentukan dengan menghitung kemiringan garis {(x1 , f (x1 )), (x2 , 0)}
dan kemiringan garis {(x2 , 0), (x0 , f (x0 ))} dan ini memberikan
f (x1 ) − f (x0 )
0 − f (x1 )
=
.
x1 − x0
x2 − x1
Penyelesain persamaan diatas untuk x2 diberikan oleh,
x2 = x1 − f (x1 )
x1 − x0
f (x1 ) − f (x0 )
(4.23)
Jika proses perhitungan berulang dilakukan dengan cara yang sama, maka dengan
menggunakan x0 , x1 akan diperoleh barisan x2 , x3 , . . . yang akan menghampiri akar persamaan α dan persamaan (4.23) menjadi,
xn+1 = xn − f (xn )
xn − xn−1
f (xn ) − f (xn−1 )
(4.24)
Iterasi metode Secant akan dihentikan jika memenuhi kondisi sebagai berikut.
1. |xn+1 − xn | < , di mana adalah toleransi
x
n+1 − xn 2. < δ di mana δ adalah galat hampiran.
xn+1
Teorema 4.3 Algoritma Metode Secant
Untuk menentukan akar f (x) = 0, diberikan dua nilai x0 dan x1 dan dengan
menggunakan iterasi
xn+1 = xn −
f (xn ) − xn−1
f (xn ) − f (xn−1 )
.
Algoritma metode Secant adalah sebagai berikut.
Contoh 4.10
Tentukan penyelesaian positif dari f (x) = x − 2 sin x = 0 dengan menggunakan metode
Secant, dengan mengambil titik awal x0 = 2 dan x1 = 1, 9
Penyelesaian:
Dari formula Secant diperoleh,
xi+1 = xi −
(xi − 2 sin xi )(xi − xi−1 )
xi − xi−1 + 2(sin xi−1 − sin xi )
4.3 Metode Secant
81
INPUT tebakan awal x0,x1, toleransi tol
OUPUT akar persamaan
Algoritma
1. repeat x_lama <--x1
x:=x-(f(x1)*(x1-x0)/(f(x1)-f(x0))
x0<--x1
x1<--x
kembali ke 1
2. | x-xlama| < e
3. tulis akar x
atau
xi+1 = xi −
Ni
Di
dengan
Ni = (xi − 2 sin xi )(xi − xi−1 ) dan Di = xi − xi−1 + 2(sin xi−1 − sin xi )
Hasil perhitungan secara numerik diperlihatkan pada Tabel 4.7
Tabel 4.7 Perbadingan kecepatan konvergensi Newton-Raphson baku dan
modifikasi pada kasus f (x) = x3 − 5x2 + 7x − 3 dengan nilai awal
x0 = 0
n
xn−1
xn
Nn
Dn
xn+1 − xn
1
2
3
2,000000
1,900000
1,895747
1,900000
1,895747
1,895494
-0,000740
-0,000002
0
-0,174005
-0,006986
-0,004253
-0,000252
0
Latihan
4.3
1. Gunakan metode Newton-Raphson untuk menyelesaikan persoalan-persoalan berikut.
a. sin x = cot x,
b. x = cos x,
x0 = 1
x0 = 1
82
Bab 4 Akar-Akar Persamaan Nonlinear
c. x3 − 5x + 3 = 0,
d. x + ln x = 2,
x0 = 2
x0 = 2
e. ex + 2−x + 2 cos x − 6 = 0,
untuk
[1, 2]
f. ln(x − 1) + cos(x − 1) = 0,
untuk
[1, 3; 2]
g. 2x cos 2x − (x − 2)2 = 0,
untuk
[2, 3]
2. Gunakan metode Secant untuk menyelesaikan persoalan-persoalan berikut.
a. x3 − 5x + 3 = 0,
x0 = 0.5, x1 = 2, 0
b. e−x − tan x = 0,
x0 = 1, x1 = 0, 7
c. sin x = cot x,
d. x = cos x,
x0 = 1, x1 = 0, 5
x0 = 0, 5, x1 = 1
e. cos x = x = 0,
x0 = 0.5, x1 = 1
f. x + ln(x) = 2,
x0 = 1, x1 = 2
BAB 5
INTERPOLASI
5.1
Pengantar
Polinomial Taylor sering digunakan sebagai pendekatan dalam menginterpolasi
suatu fungsi, dan oleh karena pada pendekatan Taylor hanya menggunakan satu titik,
maka pendekatan ini masih mempunyai kelemahan. Pendekatan dengan menggunakan
polinomial Taylor hanya akurat hanya disekitar titik tersebut. Oleh karena itu, perlu
suatu pendekatan dengan melibatkan banyak titik, yang biasa disebut Polinomial Lagrange.
Pada polinomial Taylor yang diberikan pada bab sebelumnya, yang menggambarkan sala satu asas untuk membangun bagian analisis numerik. Polinomial Taylor
cukup baik untuk digunakan terhadap suatu fungsi yang diberika pada titik tertentu,
yang memfokuskan keakuratannya hanya disekitar titik tersebut. Polinomial yang baik
membutuhkan banyak titik untuk memberikan pendekatan yang cukup akurat pada
interval tertentu.
Sebagai contoh, misalkan kita akan menghitung enam suku pertama terhadap
fungsi ex disekitar x0 = 0 dengan menggunakan polinomial Taylor, yang diberikan oleh,
P0 (x) = 1,
P1 (x) = 1 + x,
x2
,
2
x2
P3 (x) = 1 + x +
+
2
x2
P4 (x) = 1 + x +
+
2
x2
P5 (x) = 1 + x +
+
2
P2 (x) = 1 + x +
x3
,
6
x3
+
6
x3
+
6
x4
,
24
x4
x5
+
24 120
84
Bab 5 Interpolasi
Nilai-nilai dari hasil pendekatan polinomial Taylor diberikan pada Tabel 5.1 untuk beberapa nilai x.
Tabel 5.1 Hasil perhitungan enam suku pertama polinomial Taylor terhadap
fungsi f (x) = ex disekitar x = 0
x
P0 (x)
P1 (x)
P2 (x)
P3 (x)
P4 (x)
P5 (x)
ex
-2,0
-1,5
0
1,0
2,0
1,00000
1,00000
1,00000
1,00000
1,00000
-1,00000
-0,50000
1,00000
2,00000
3,00000
1,00000
0,62500
1,00000
2,50000
5,00000
-0,33333
0,06250
1,00000
2,66667
6,33333
0,33333
0,27344
1,00000
2,70833
7,00000
0,06667
0,21016
1,00000
2,71667
7,26667
0,13534
0,22313
1,00000
2,71828
7,38906
Dari tabel tersebut dapat kita lihat bahwa semakin tinggi orde pendekatan, maka
galat yang dihasilkan akan semakin kecil. Namun hal ini tidak terjadi pada semua kasus.
Pertimbangkan contoh yang cukup ekstrim untuk menunjukkan bahwa orde pada
polinomial Taylor tidak berlaku untuk beberapa kasus. Gunakan polinomial Taylor
untuk mengiterpolasi fungsi f (x) = 1/x disekitar titik x = 1.
P0 (x) = 1,
P1 (x) = 1 + −(x − 1),
P2 (x) = 1 + −(x − 1) + (x − 1)2 ,
P3 (x) = 1 + −(x − 1) + (x − 1)2 − (x − 1)3 ,
P4 (x) = 1 + −(x − 1) + (x − 1)2 − (x − 1)3 + (x − 1)4 ,
P5 (x) = 1 + −(x − 1) + (x − 1)2 − (x − 1)3 + (x − 1)4 − (x − 1)5
..
.
Secara umum, bentuk polinomial diatas dapat ditulis,
Pn (x) = f (1) +
=
n
f (1) f (1)
f n (1)
+
(x − 1)2 + · · · +
(x − 1)n
k!
2!
n!
(−1)k (x − 1)k
k=0
Nilai-nilai dari pendekatan Taylor diberikan pada Tabel 5.2.
5.1 Pengantar
85
Tabel 5.2 Hasil perhitungan enam suku pertama polinomial Taylor terhadap
fungsi f (x) = 1/x disekitar x0 = 1
x
P0 (x)
P1 (x)
P2 (x)
P3 (x)
P4 (x)
P5 (x)
P6 (x)
P7 (x)
f (x) = 1/x
3
1
-1
3
-5
11
-21
43
-85
3,33333
Dari tabel 5.2, jelas terlihat bahwa nilai-nilai meningkat secara drastis, namun
jauh dari nilai yang diinginkan.
Dari beberapa kasus yang terjadi pada pendekatan polinomial Taylor, maka dikenalkan Polinomial yang menggunakan beberapa titik sebagai informasi untuk menentukan pendakatan.
Polinomial ini mengembangkan interpolasi terhadap suatu fungsi dibeberapa
titik terhubung, sehingga interpolasinya berdasarkan titik yang telah ditentukan terlebih
dahulu. Semakin dekat jarak antar titik, maka semakin akurat hasil pendekatannya.
Interpolasi adalah proses penentuan dan evaluasi fungsi yang mana grafik atau
kurvanya di peroleh dari sekumpulan titik. Titik-titik tersebut mungkin muncul atau
diperoleh dari persoalan-persoalan fisika, atau dari fungsi yang tidak diketahui. Interpolasi fungsi biasanya dipilih dari fungsi terbatas yang digunakan untuk menyelesaikan
persoalan dari sebagian besar teori hampiran.
Nilai-nilai yang diperoleh biasanya berupa pasangan terurut yang ditulis,
(x0 , f0 ), (x1 , f1 ), (x2 , f2 ), · · · (xn , fn )
Masalah yang muncul dari sekumpulan data-data atau titik-titik yang diberikan
adalah menentukan nilai diantara data-data tersebut. Salah satu solusi yang dapat
dilakukan adalah mencari fungsi dengan mencocokan (fit) titik-titik data di dalam tabel
tersebut. Pendekatan seperti ini disebut pencocokan kurva (curve fitting). Fungsi yang
diperoleh dengan cara seperti ini adalah kurva hampiran. Pencocokan kurva tidak
hanya untuk menentukan suatu fungsi, tetapi juga digunakan untuk mempermudah
perhitungan numerik yang lainnya, seperti menghitung nilai turunan dan integral.
Pencocokan kurva merupakan metode yang mencocokan sekumpulan titik data
86
Bab 5 Interpolasi
dengan kurva (curve fitting) fungsi, yang dilakukan dengan dua cara:
1. Regresi
Misalnya, terdapat titik-titik hasil pengukuran yang mengandung derau (noise)
atau galat yang cukup berarti. Strategi yang digunakan adalah menentukan kurva
yang mewakili kecenderungan (trend) titik data, sehingga selisih antara titik data
dengan titik hampirannya dikurva sekecil mungkin. Metode ini disebut regresi
kuadrat terkecil.
2. Interpolasi
Bila data diketahui mempunyai ketelitian tinggi, maka kurva cocokannya dibuat
melalui setipa titik, dan dikatakan bahwa kita menginterpolasi titik-titik dengan
sebuah fungsi.Bila fungsi cocokan yang digunakan berbenuk polinom, maka polinom tersebut dinamakan polinom interpolasi
5.2
Interpolasi Polinom Lagrange
Jika pada suatu data terdapat n+1 buah titik yang berbeda, yaitu (x0 , y0 ), (x1 , y1 ),
(x2 , y2 ), (x3 , y3 ), · · · , (xn , yn ), maka polinom Pn (x) yang menginterpolasi semua titiktitik dapat ditentukan, sehingga
yi = Pn (xi ),
untuk
i = 1, 2, 3, · · · , n
Nilai yi dapat berasal dari fungsi matematika f (x), seperti ln x, sin x, fungsi Bessel,
fungsi Gamma, dan sebagainya, sehingga yi = f (xi ), sedangkan Pn (x) adalah fungsi
hampiran terhadap f (x). Perhatikan Gambar 5.1.
Setelah interpolasi Pn (x) ditemukan, maka Pn (x) dapat digunakan untuk menghitung perkiraan nilai-nilai yang terletak diantara x0 dan xn , biasa disebut mengiterpolasi,
atau memperkirakan nilai-nilai yang terletak di luar x0 , biasa disebut ekstrapolasi.
5.2.1
Interpolasi Linear
Sebagian besar orang menggunakan interpolasi di dalam aljabar elementer yang mana
menggunakan tabel fungsi logaritma atau trigonometri untuk menentukan nilai lain
yang tidak diberikan pada tabel. Bentuk interpolasi yang digunakan tersebut adalah
5.2 Interpolasi Polinom Lagrange
87
Y 6
(xn−1 , yn−1 )
s
(x1 , y1 )
s s(x2 , y2 )
s(xn , yn )
s
s(x0 , y0 )
(x3 , y3 )
X
-
Gambar 5.1 Interpolasi (garis tebal) dan ekstrapolasi (garis tipis) terhadap
titik-titik yang diberikan.
interpolasi linear, yang merupakan pengantar dari sebagai besar interpolasi yang digunakan sekarang.
Misalkan diberikan dua titik (x0 ), y0 ) dan (x1 , y1 ) dengan x0 = x1 , selanjutnya
kita tarik garis lurus yang melewati kedua titik tersebut, sebagaimana ditunjukkan pada
Gambar 5.2.
Y
(x1 , y1 )
•
• P1 (x)
f (x)
(x0 , y0 ) •
X
x0
x
x1
Gambar 5.2 Interpolasi linear y = P1 (x)
Polinom yang mengiterpolasi kedua titik itu adalah persamaan garis lurus yang
berbentuk,
P1 (x) = a0 + a1 (x)
(5.1)
Koefisien a0 dan a1 dicari dengan proses menyulihan (x0 , y0 ) dan (x1 , y1 ) ke
88
Bab 5 Interpolasi
dalam persamaan (5.1), diperoleh dua persamaan linear,
y0 = a0 + a1 x0
y1 = a0 + a1 x1
Dan dengan mengeleminasi kedua persamaan tersebut, diperoleh,
y1 − y 0
, dan
x1 − x0
x1 y0 − x0 y1
a0 =
x1 − x0
a1 =
(5.2)
(5.3)
Substitusikan persamaan (5.2) dan (5.3) ke dalam persamaan (5.1), maka diperoleh,
x1 y0 − x0 y1 (y1 − y0 )x
+
h
x1 − x0
x1 − x0
x1 y0 − x0 y0 + x0 y0 − x0 y1 + y1 x − y0 x
=
x1 − x0
y0 (x1 − x0 ) + y1 (x − x0 ) − y0 (x − x0 )
=
x1 − x0
(y1 − y0 )
= y0 +
(x − x0 )
x1 − x0
P1 (x) =
(5.4)
Bentuk terakhir dapat diubah menjadi,
(x − x0 )
(x − x0 )
+ y1
(x1 − x0 )
(x1 − x0 )
(x − x0 )
y0 (x1 − x0 ) − y0 (x − x0 )
+ y1
=
(x1 − x0 )
(x1 − x0 )
(x − x1 )
(x − x0 )
+ y1
= y0
(x0 − x1 )
(x1 − x0 )
P1 (x) = y0 − y0
(5.5)
atau
P1 (x) = y0 L0 (x) + y1 L1 (x)
dengan
L0 (x) =
(x − x1 )
(x0 − x1 )
L1 (x) =
(5.6)
(x − x0 )
(x1 − x0 )
Persamaan (5.6) disebut polinomial Lagrange Linear.
Oleh karena grafik polinomial linear yang berbentuk garis lurus tersebut dihitung dengan (x0 , y0 ) dan (x1 , y1 ), sehingga dapat kita katakan interpolasi untuk yn pada
titik xn , n = 0, 1
5.2 Interpolasi Polinom Lagrange
89
Contoh 5.1
Misalkan diberikan titik-titik (1, 1) dan (4, 2), tentukan interpolasi linearnya.
Penyelesaian:
Garis yang melalui titik (1, 1) dan (4, 2), maka interpolasi linearnya adalah
P1 (x) =
=
(4 − x)(1) + (x − 1)(2)
4−1
x+2
3
Contoh 5.2
Diketahui data jumlah penduduk Amerika Serikat sebagai berikut.
Tahun
Jumlah penduduk (juta)
1960
179,3
1970
203,2
Tentukan jumlah penduduk pada tahun 1968.
Penyelesaian:
179, 3 + 203, 2 − 179, 3(x − 1960)
1970 − 1960
382, 5 − 179, 3(x − 1960)
=
10
= 38, 25 − 17, 93(x − 1960)
P1 (x) =
P1 (1968) = 38, 25 − 17, 93(1968 − 1960)
= 198, 4
Jadi, perkiraan jumlah penduduk Amerika Serikat pada tahun 1968 adalah 198,4 juta
jiwa.
Contoh 5.3
Tentukan nilai e0,826 dari perkiraan nilai-nilai yang diberikan pada Tabel 5.3.
Penyelesaian:
90
Bab 5 Interpolasi
Tabel 5.3 Perkiraann nilai-nilai dari fungsi ex
x
ex
0,80
0,81
0,82
0,83
0,84
2,225541
2,247908
2,270500
2,293319
2,316367
Untuk menentukan nilai e0,826 , maka terlebih dahulu ditentukan polinom linear yang
diambil dari titik x = 0, 82 dan x = 0, 83,
(0, 83 − x)(2, 270500) + (x − 82)(2, 293319)
0, 83 − 0, 82
0, 00399342 + 0, 022819x
=
0, 01
= 0, 399342 + 2, 2819x
P1 (x) =
dan nilai untuk x = 0, 826 adalah
P1 (0, 286) = 2, 2841914
Contoh 5.4
Hitunglah nilai ln 9, 2 sampai dengan 4 desimal dari titik-titik ln 9, 0 = 2, 1972 dan
ln 9, 5 = 2, 2513 dengan menggunakan pendekatan polinomial Lagrange linear.
Penyelesaian:
Dari soal yang diberikan dapat diperoleh informasi sebagai berikut.
x0 = 9, 0 ; x1 = 9, 5 ; y0 = 2, 1972 ; y1 = 2, 2513
. Dari persamaan (5.6) diperoleh
(x − x1 )
(x − 9, 5)
=
(x0 − x1 )
9, 0 − 9, 5
= −2, 0(x − 9, 5)
L0 (x) =
L0 (9, 2) = −2, 0(9, 2 − 9, 5)
= 0, 6
5.2 Interpolasi Polinom Lagrange
91
(x − 9, 0)
(x − x0 )
=
(x1 − x0 )
9, 5 − 9, 0
= 2, 0(x − 9, 0)
L1 (x) =
L0 (9, 2) = 2, 0(9, 2 − 9, 0)
= 0, 4
Jadi,
ln(9, 2) ≈ P1 (9, 2) = L0 (9, 2)y0 + L1 (9, 2)y1
= (0, 6)(2, 1972) + (0, 4)(2, 2513)
= 2, 2188
5.2.2
Interpolasi Kuadratik
Sebelumnya kita telah mempelajari polinom linear sebagai dasar untuk pengembangan
bentuk-bentuk polinom dengan pangkat yang lebih tinggi. Pada kenyataannya, pendekatan dengan polinom lienar kurang baik. Untuk pendekatan dengan polinom yang
lebih tinggi akan banyak membantu menyelesaikan persoalan-persoalan yang muncul.
Y
(x2 , y2 )
•
(x1 , y1 )
• •
P2 (x)
f (x)
(x0 , y0 ) •
X
x0
x1 x
x2
Gambar 5.3 Interpolasi kuadratik y = P2 (x)
Misalkan diberikan tiga titik (x0 , y0 ), (x1 , y1) dan (x3 , y3 ). Kita akan membentuk
polinomial kuadratik dari tiga titik tersebut, yaitu
P2 (x) = a0 + a1 (x) + a2 x2
(5.7)
92
Bab 5 Interpolasi
Selanjutnya subsitusikan titik-titik (x0 , y0 ), (x1 , y1) dan (x3 , y3 ) ke dalam persamaan
(5.7), sehingga diperoleh tiga buah persamaan dengan tiga parameter tak diketahui,
yaitu a0 , a1 dan a2 , dengan persamaan,
y0 = a0 + a1 x0 + a2 x20
y1 = a0 + a1 x1 + a2 x21
y2 = a0 + a1 x2 + a2 x22
Dengan menyelesaikan sistem persamaan di atas secara serentak untuk a0 , a1 dan a3 ,
maka diperoleh,
P2 (x) = y0 L0 (x) + y1 L1 (x) + y2 L2 (x)
(5.8)
dengan
L0 (x) =
L1 (x) =
L2 (x) =
(x − x1 )(x − x2 )
(x0 − x1 )(x0 − x2 )
(x − x0 )(x − x2 )
(x1 − x0 )(x1 − x2 )
(x − x0 )(x − x1 )
(x2 − x0 )(x2 − x1 )
Bentuk persamaan (5.8) adalah rumus Lagrange untuk interpolasi kuadratik dan polinomial L0 (x), L1 (x), L2 (x) adalah fungsi dasar Lagrange. Persamaan (5.8) dapat dibentuk
kembali menjadi bentuk umum,
1
P2 (x) = y0 + µ(y1 − y0 ) + (µ − 1) [(y2 − y1 ) − (y1 − y0 )]
2
atau
1
P2 (x) = P1 (x) + (µ − 1) [(y2 − y1 ) − (y1 − y0 )]
2
(5.9)
dengan µ = (x − x0 )/(x1 − x0 ).
Contoh 5.5
Hitung interpolasi kuadratik dari nilai-nilai Tabel 5.3 untuk x = 0, 826.
Penyelesaian:
Untuk menghitung e0,826 , kita akan pilih tiga titik yang berdekatan dari tabel, yaitu
x0 = 0, 82;
x1 = 0, 83;
x2 = 0, 84.
5.2 Interpolasi Polinom Lagrange
93
Dari tiga titik diperoleh,
x − x0
x1 − x0
0, 826 − 0, 82
=
0, 83 − 0, 82
= 0, 6
µ =
sedangkan untuk y1 − y0 = 0, 022819
dan
y2 − y1 = 0, 023048
Interpolasi kuadratik berdasarkan rumus pada persamaan (5.9), diperoleh
1
P2 (x) = P1 (x) + (0, 6)(0, 6 − 1)90, 023048 − 0, 022819)
2
= 2, 2841914 − 0, 00002748
= 2, 2841639
Contoh 5.6
Hitunglah ln 9, 2 sampai empat desimal dari titik-titik ln 9, 0 = 2, 1972, ln 9, 5 = 2, 2513
dan ln 11, 0 = 2, 3979 dengan menggunakan pendekatan polinomial kuadratik.
Penyelesaian:
Dari soal yang diberikan, dan dengan menggunakan persamaan (5.9dapat kita tentukan,
(x − 9, 5)(x − 11, 0)
= x2 − 20, 5x + 104, 5
(9, 0 − 9, 5)(9, 0 − 11, 0)
L0 (9, 2) = 0, 5400
L0 (x) =
1
(x − 9, 0)(x − 11, 0)
=−
(x2 − 20x + 99)
(9, 5 − 9, 0)(9, 5 − 11, 0)
0, 75
L1 (9, 2) = 0, 4800
L1 (x) =
1
(x − 9, 0)(x − 9, 5)
= − (x2 − 18, 5x + 85, 5)
(11 − 9, 0)(11 − 9, 5)
3
L2 (9, 2) = −0, 0200
L2 (x) =
jadi,
ln(9, 2) ≈ P2 (9, 2) = (0, 5400)(2, 1972) + (0, 4800)(2, 2513) − (0, 0200)(2, 3979)
= 2, 2192
94
Bab 5 Interpolasi
Contoh 5.7
Diberikan x0 = 2, x1 = 2, 5 dan x2 = 4, tentukan interpolasi kuadratik dari f (x) = 1/x
untuk x = 3.
Penyelesaian:
Langkah pertama yang harus dilakukan adalah menentukan koefisien polinomial
L0 (x) =
L1 (x) =
L2 (x) =
(x − 2, 5)(x − 4)
= (x − 6, 5)x + 10
(2 − 2, 5)(2 − 4)
(−4x + 24)x − 32
(x − 2)(x − 4)
=
(2, 5 − 2)(2, 5 − 4)
3
(x − 4, 5)x + 5
(x − 2)(x − 2, 5)
=
(4 − 2)(4 − 2, 5)
3
Oleh karena,
f (x0 ) = f (2) = 0, 5, f (x1 ) = f (2, 5) = 0, 4, f (x2 ) = f (4) = 0, 25, maka
P (x) =
2
yk Lk (x)
k=0
= 0, 5((x − 6, 5)x + 10) + 0, 4(
(−4x + 24)x − 32
(x − 4, 5)x + 5
) + 0, 25(
)
3
3
= (0, 05x − 0, 425)x + 1, 15
Jadi, f (x) diperoleh dengan pendekatan P (x), untuk itu
f (3) ≈ P (x) = 0, 325
5.2.3
Interpolasi Derajat Tinggi
Sekarang kita pertimbangkan kasus secara umum. Andaikan diberikan sejumlah (n +
1) data atau titik (x0 , y0 ), (x1 , y1 ), . . . , (xn , yn ) dan semua titik-titik tersebut adalah
berbeda, maka interpolasi polinomial derajat ≤ n diberikan oleh
Pn (x) = y0 L0 (x) + y1 L1 (x) + · · · + yn Ln (x)
yang mana setiap Li (x) adalah polinomial derajat n yang diberikan oleh,
Li (x) =
(x − x0 ) · · · (x − xi−1 )(x − xi+1 ) · · · (x − xn )
(xi − x0 ) · · · (xi − xi−1 )(xi − xi+1 ) · · · (xi − xn )
(5.10)
5.2 Interpolasi Polinom Lagrange
95
Y
5
3
f (x)
1
•
P2 (x)
O
1
2
3
X
4
5
6
7
Gambar 5.4 Interpolasi polinomial kuadratik y = P2 (x) terhadap fungsi f =
1/x
untuk 0 ≤ i ≤ n. Pembagi-pembaginya sama dengan pembilangan pada x = xi, yang
mana Li (x) memenuhi,
Li (xj ) = δij ,
0≤j≤n
(5.11)
untuk i = 0, 1, . . . , n. Dengan menggunakan persamaan (5.11), dengan substitusi langsung x = xj , diperoleh
Pn (xj ) = yj ,
Teorema 5.1
j = 0, 1, . . . , n
(5.12)
96
Bab 5 Interpolasi
Jika x0 , x1 , . . . , xn adalah (n + 1) bilangan yang berbeda dan f adalah fungsi kontinu
yang dihitung pada setiap nilai tersebut, maka terdapat polinomial P berderajat
paling tinggi n yang memenuhi
f (xk ) = P (xk ),
untuk setiap k = 0, 1, . . . , n
dan polinomial ini diberikan oleh,
P (x) = f (x0 )L0 (x) + f (x1 )L1 (x) + · · · + f (xn )Ln (x) =
n
f (xk )Ln (x)
(5.13)
k=0
di mana
Lk (x)
=
=
(x − x0 )(x − x1 )(x − x2 ) · · · (x − xk−1 )(x − xk+1 ) · · · (x − xn )
(xk − x0 )(xk − x1 )(xk − x2 ) · · · (xk − xk−1 )(xk − xk+1 ) · · · (xk − xn )
n
(x − xi )
(5.14)
(x
k − xi )
i=0
i=0
Teorema 5.2
Jika x0 , x1 , . . . , xn adalah (n + 1) bilangan yang berbeda pada interval [a, b]
dan f ∈ C n+1 [a, b], maka untuk setiap x dalam [a, b] dan sebuah bilangan ξ(x)
pada (a, b) terdapat,
f (x) = P (x) +
f n+1 (ξ(x))
(x − x0 )(x − x1 ) · · · (x − xn ),
(n + 1)!
(5.15)
dengan P adalah interpolasi polinomial yang diberikan pada persamaan (5.13)
Perlu diperhatikan bahwa, galat dari polinomial Lagrange hampir sama dengan
bentuk galat polinomial Taylor. Galat polinomial Taylor pada derajat ke-n disekitar
x0 , diberikan oleh
f (n+1) (ξ(x))
(x − x0 )n+1
(n + 1)
sedangan galat polinomial Lagrange pada derajat ke-n menggunakan semua informasi
dari x1 , x2 , . . . , xn di sekitar (x − x0 )n . Jadi galat menggunakan perkalian dari (n + 1
suku (x − x0 ), (x − x1 ), (x − x2 ), . . . , (x − xn ) yang diberikan oleh
f (n+1) (ξ(x))
(x − x0 )(x − x1 ), · · · , (x − xn )
(n + 1)
5.2 Interpolasi Polinom Lagrange
97
30
20
10
–1
1
2
3
4
5
x
–10
–20
Gambar 5.5 Interpolasi kubik y = P3 (x)
Contoh 5.8
Gunakan Tabel 5.4untuk menghitung nilai pendekatan f (1, 5) dengan menggunakan
Polinomial Lagrenge dan bandingkan! Polinomial Linear
Tabel 5.4 Nilai-nilai dari f (x) = ex
x
ex
1,0
1,3
1,6
1,9
2,2
0,7651977
0,6200860
0,4554022
0,2818186
0,1103623
Oleh karena 1,5 berada diantara 1,3 dan 1,6 , kita akan menggunakan polinomial linear,
yaitu x0 = 1, 3 dan x1 = 1, 6. Nilai-nilai interpolasi polinomial pada 1,5 diberikan oleh,
P1 (x) = y0 L1 (x) + y1 L1 (x)
(x − x1 )
(x − x0 )
= y0
+ y1
(x0 − x1 )
(x1 − x0 )
98
Bab 5 Interpolasi
P1 (1, 5) = 0, 6200860y
(1, 5 − 1, 3)
(1, 5 − 1, 6)
+ 0, 4554022
(1, 3 − 1, 6)
(1, 6 − 1, 3)
= 0, 5102968
Polinomial kuadratik
Kita gunakan titik-titik x0 = 1, 3; x1 = 1, 6 dan x2 = 1, 9, dan
(1, 5 − 1, 3)(1, 5 − 1, 9)
(1, 5 − 1, 6)(1, 5 − 1, 9)
+ (0, 4554022)
(1, 3 − 1, 6)(1, 3 − 1, 9)
(1, 6 − 1, 3)(1, 6 − 1, 9)
(1, 5 − 1, 3)(1, 5 − 1, 6)
+(0, 2818186)
(1, 9 − 1, 3)(1, 9 − 1, 6)
= 0, 5112857
P2 (1, 5) = (0, 6200860)
alternatif lain, kita ambil x0 = 1, 0; x1 = 1, 3 dan x2 = 1, 6, diperoleh
Pˆ2 (1, 5) = 0, 5124715
Polinomial kubik
Pada pendekatan polinomial pangkat tiga, terdapat dua alternatif,
ambil empat titik, yaitu x0 = 1, 3; x1 = 1, 6; x2 = 1, 9 dan x3 = 2, 2, dan diperoleh
P3 (1, 5) = 0, 5118302
Alternatif lain, kita ambil empat titik, yaitu x0 = 1, 0; x1 = 1, 3; x2 = 1, 6 dan x3 = 1, 9,
maka diperoleh
Pˆ3 (1, 5) = 0, 5118127
Untuk polinomial pangkat empat, hanya satu alternatif dan kita akan menggunakan
semua titik, yaitu x0 = 1, 0; x1 = 1, 3; x2 = 1, 6; x3 = 1, 9 dan x4 = 2, 2, maka diperoleh,
P4 (x) = 0, 5118200
Jika nilai sejati f (1, 5) = 0, 5118277, maka dapat kita tentukan dari beberapa pendekatan yang telah digunakan, mana pendekatan yang paling akurat,
|P1 (1, 5) − f (1, 5)| ≈ 1, 53 × 10−3 ,
|P2 (1, 5) − f (1, 5)| ≈ 5, 42−4 ,
|Pˆ2 (1, 5) − f (1, 5)| ≈ 6, 44 × 10−4 ,
|P3 (1, 5) − f (1, 5)| ≈ 2, 5 × 10−6 ,
5.2 Interpolasi Polinom Lagrange
99
|Pˆ3 (1, 5) − f (1, 5)| ≈ 1, 50 × 10−5 ,
|P4 (1, 5) − f (1, 5)| ≈ 7, 7 × 10−6
Latihan
5.1
1. Gunakan interpolasi Lagrange untuk mengiterpolasi polinomial berderajat satu,
dua, tiga dan empat pada setiap persoalan berikut.
a. f (8, 4) jika f (8) = 16, 63553, f (8, 1) = 17, 61549,
f (8, 3) = 17, 56492, f (8, 6) = 18, 50515, f (8, 7) = 18, 82091
b. f (0, 25) jika f (0) = −1, f (−0, 1) = −0, 62049958, f (0, 2) = −0, 28398668,
f (0, 3) = 0, 00660095, f (0, 4) = 0, 24842440
c. f (0, 9) jika f (0, 5) = −0, 3440983, f (0, 6) = −0, 17694460,
f (0, 7) = 0, 01375227, f (0, 8) = 0, 22363362, f (1, 0) = 0, 65809197
d. f (1, 15) jika f (1) = 1, 684370, f (1, 1) = 1, 949477,
f (1, 2) = 2, 199796, f (1, 3)2, 439189, f (1, 4) = 2, 670324
2. Gunakan hasil interpolasi data-data pada soal no 1(a),(b),(c) dan bandingkan
dengan fungsi-fungsi berikut untuk menentukan batas galat
a. f (x) = ln(x)
b. f (x) = x3 + 4, 001x2 + 4, 002x + 1, 101
c. f (x) = x cos x − 2x2 + 3x − 1
3. Buatlah interpolasi polinomial Lagrange dari fungsi-fungsi berikut berdasarkan
titik-titik yang diberikan.
a. f (x) = e2x cos(3x),
x0 = 1,
d. f (x) = cos(x) + sin(x),
4. Misalkan f (x) = ex ,
untuk menghitung:
x1 = 0, 3 x2 = 0, 6
x0 = 2, 0 x1 = 2, 4 x2 = 2, 6
b. f (x) = sin(ln(x)),
c. f (x) = ln(x),
x0 = 0,
x1 = 1, 1 x2 = 1, 2 x3 = 1, 4
x0 = 0,
x1 = 0, 25 x2 = 0, 5 x3 = 1, 0
0 ≤ x ≤ 2. Gunakan nilai-nilai yang diberikan berikut
100
Bab 5 Interpolasi
a. Hampiran interpolasi linear f (0, 25) dengan x0 = 0 dan x1 = 0, 5
b. Hampiran interpolasi linear f (0, 75) dengan x0 = 0, 5 dan x1 = 1
c. Untuk soal (a) dan (b), gunakan hampiran interpolasi kuadratik dengan x0 =
0, x1 = 1 dan x2 = 2
d. Yang manakah hampiran yang lebih baik?
x
0,0
0,5
1,0 2,0
y 1,00000 1,64872 2,71828
7,38906
5. Diberikan titik-titik (0, 2), (1, 1), tentukan:
(a) Interpolasi garis lurus dari data tersebut
(b) Interpolasi fungsi f (x) = a + bex ,
petunjuk : temukan a dan b sehingga f (0) = 2, f (1) = 1
(c) Interpolasi fungsi f (x) = a/(b + x)
6. Dengan menggunakan Tabel 5.3, tentukan interpolasi linear untuk:
(a) e0,865
(b) e5/6
Bandingkan yang diperolehnya terhadap nilai sebenarnya.
7. Hitunglah fungsi P (x) = a+b cos(πx)+c sin(πx) yang diinterpolasi oleh data-data
sebagai berikut.
x
y
0
2
1
2
5
1
4
8. Misalkan xj = j untuk j = 0, 1, 2, 3 dan diketahui bahwa
P0,1 (x) = x + 1,
P1,2 (x) = 3x − 1,
P1,2,3 (1, 5) = 4
tentukan P0,1,2,3 (1, 5)
Petunjuk :
P0,1,2,3 (x) artinya interpolasi yang menggunakan titik x0 , x1 , x2 , x3
9. Misalkan xj = j untuk j = 0, 1, 2, 3 dan diketahui bahwa
P0,1 (x) = 2x + 1,
tentukan P0,1,2,3 (2, 5)
P0,2 (x) = x + 1,
P1,2,3 (2, 5) = 3
5.3 Selisih Terbagi Newton
101
10. Buatlah interpolasi polinomial kuadratik untuk data {(−2, −15), (−1, −8), (0, −3)}.
Tentukan nilai nol P2 (x) untuk x = 0. Apakah P2 (x) mempunyai nilai maksimum?
11. Untuk n = 3, jelaskan mengapa
L0 (x) + L1 (x) + L2 (x) + L3 (x) = 1
untuk semua nilai x
12. Sebuah permasalahan yang diperumum, tentukan polinomial kuadratik Q(x) yang
mana
Q(0) = −1,
5.3
Q(1) = −1,
Q (1) = 4
Selisih Terbagi Newton
Iterasi interpolasi digunakan untuk mengeneralkan pendekatan polinomial der-
ajat yang lebih tinggi untuk titik-titik tertentu. Metode selisih terbagi akan diperkenalkan pada sub-bab ini secara ringkas.
Misalkan bahwa Pn (x) adalah polinomial Lagrange ke-n yang dekat dengan
fungsi f pada bilangan-bilangan berbeda x0 , x1 , x2 , . . . , xn , maka selisih terbagi f yang
berkaitan dengan x0 , x1 , x2 , . . . , xn ,
Pn (x) = a0 + a1 (x − x0 ) + a2 (x − x0 )(x − x1 ) + · · ·
an (x − x0 )(x − x1 )(x − x2 ) · · · (x − xn−1 )
(5.16)
untuk konstanta a0 , a1 , a2 , . . . , an .
Untuk menghitung konstanta a0 , maka kita akan mengevaluasi persamaan (5.16)
pada x0 dan hanya meninggalkan konstanta a0 ,
Pn (x0 = f (x0 ) = a0 + a1 (0) + a2 (0) + · · · + an (0)
f (x0 ) = a0
(5.17)
Dengan cara yang sama, kita akan mengevaluasi Pn (x) pada x = x1 ,
Pn (x1 ) = f (x1 ) = a0 + a1 (x1 − x0 ) + a2 (0) + a3 (0) + · · · + an (0)
f (x1 ) = a0 + a1 (x1 − x0 )
(5.18)
102
Bab 5 Interpolasi
dengan mensubstitusikan a0 = f (x0 ), maka persamaan di atas, maka
f (x1 ) = f (x0 ) + a1 (x1 − x0 )
atau
a1 =
f (x1 ) − f (x0 )
(x1 − x0 )
Bentuk di atas dapat ditulis,
f [x0 , x1 ] =
f [x1 ] − f [x0 ]
x1 − x0
(5.19)
Bentuk ungkapan pada persamaan (5.19) disebut selisih terbagi orde pertama. Jika
selisih terbagi ke-0 dari fungsi f yang berkaitan dengan xi adalah f [xi ], atau lebih
sederhana
f [xi ] = f (xi )
maka selisih terbagi pertama dari fungsi f terhadap xi dan xi+1 dilambangkan dengan
f [xi , xi+1 ], dan didefinisikan
f [xi , xi+1 ] =
f [xi+1 ] − f [xi ]
xi+1 − xi
Dengan cara yang sama, polinom kuadratik dapat dinyatakan dalam bentuk,
P2 (x2 ) = f (x2 ) = a0 + a1 (x2 − x0 ) + a2 (x2 − x0 )(x2 − x1 )
f (x2 ) − a0 − a1 (x2 − x0 )
a2 =
(x2 − x0 )(x2 − x1 )
f (x1 ) − f (x0 )
f (x2 ) − f (x0 ) −
(x2 − x0 )
(x1 − x0 )
=
(x2 − x0 )(x2 − x1 )
f (x2 ) − f (x0 ) f (x1 ) − f (x0 )
−
x2 − x0
x1 − x0
=
x2 − x1
(5.20)
Dengan melakukan manipulasi aljabar diperoleh,
f (x2 ) − f (x0 ) f (x1 ) − f (x0 )
−
f [x2 , x1 ] − f [x1 , x0 ]
x2 − x1
x1 − x0
=
a2 =
x2 − x0
x2 − x0
atau
f [x0 , x1 , x2 ] =
f [x2 , x1 ] − f [x1 , x0 ]
x2 − x0
(5.21)
(5.22)
5.3 Selisih Terbagi Newton
103
Secara umum selisih terbagi kedua dari fungsi f terhadap xi , xi+1 dan xi+2 , ditulis
f [xi , xi+1 , xi+2 ] =
f [xi+1 , xi+2 ] − f [xi+1 , xi ]
xi+2 − xi
Untuk selanjutnya, terdapat n + 1 bilangan real yang berbeda, x0 , x1 , x2 , · · · , xn , maka
dapat didefinsikan
f [x0 , x1 , x2 , · · · , xn ] =
f [x1 , x2 , · · · , xn ] − f [x0 , x1 , · · · , xn−1 ]
xn − x0
(5.23)
Bentuk seperti ini disebut selisih terbagi orde-n, dan kadang-kadang disebut
juga selisih terbagi Newton. Hubungan beda terbadi orde tinggi dengan derivatif
yang brekorespondensi dengan orde diberikan pada teorema berikut.
Teorema 5.3
Misalkan n ≥ 1 dan diasumsikan f (x) adalah n kali terdiferensiabel pada interval a ≤
x ≤ b dan x0 , x1 , x2 , . . . adalah n + 1 bilangan real yang berbeda pada [a, b], maka
f [x0 , x1 , . . . , xn ] =
untuk titik c yang
x0 , x1 , x2 , . . . , xn
terbentang
diantara
1 (n)
f (c)
n!
maksimum
dan
minimum
bilangan
Setelah diperoleh nilai-nilai
f [x0 ], f [x0 , x1 ], f [x0 , x1 , x2 ], . . . , f [x0 , x1 , x2 , . . . , xn ],
maka polinomial pada persamaan (5.17) dapat diubah kembali menjadi,
Pn (x) = f [x0 ] + f [x0 , x1 ](x − x0 ) + f [x0 , x1 , x2 ](x − x0 )(x − x1 ) + · · · +
f [x0 , x1 , x2 , . . . , xn ](x − x0 )(x − x1 ) · · · (x − xn−1 )
(5.24)
atau
Pn (x) = f [x0 ] +
n
f [x0 , x1 , . . . , xk ](x − x0 )(x − x1 ) · · · (x − xk−1 )
(5.25)
k=1
Bentuk persamaan terakhir biasa disebut interpolasi selisi terbagi Newton. Perhitungan selisih terbagi dapat diperoleh dari tabulasi data pada Tabel 5.5.
104
Bab 5 Interpolasi
Tabel 5.5 Selisih terbagi Newton
x
f (x)
x0
f [x0 ]
x1
f [x1 ]
ST1
ST2
ST3
ST4
f [x0 , x1 ]
f [x0 , x1 , x2 ]
f [x1 , x2 ]
x2
f [x2 ]
f [x0 , x1 , x2 , x3 ]
f [x1 , x2 , x3 ]
f [x2 , x3 ]
x3
f [x3 ]
x4
f [x4 ]
x5
f [x5 ]
f [x0 , x1 , x2 , x3 , x4 ]
f [x1 , x2 , x3 , x4 ]
f [x2 , x3 , x4 ]
f [x3 , x4 ]
f [x1 , x2 , x3 , x4 , x5 ]
f [x2 , x3 , x4 , x5 ]
f [x3 , x4 , x5 ]
f [x4 , x5 ]
Contoh 5.9
Misalkan f (x) = cos(x), x0 = 0, 2, dan x1 = 0, 3
f [x0 , x1 ] =
cos(0, 3) − cos(0, 2)
≈ 0, 2473009
0, 3 − 0, 2
dengan
f (c) ≈ − sin(0, 2498936)
dan untuk
f
x0 + x1
2
= − sin(0, 25) ≈ 0, 2474040
Contoh 5.10
Misalkan f (x) = cos(x), x0 = 0, 2, x1 = 0, 3, x2 = 0, 4 Tentukan selisih terbagi orde 2.
Penyelesaian:
f (x2 ) − f (x1 )
x2 − x1
cos(0, 4) − cos(0, 3)
=
0, 4 − 0, 3
≈ −0, 3427550
f [x1 , x2 ] =
5.3 Selisih Terbagi Newton
105
dan
f (x1 ) − f (x0 )
x1 − x0
cos(0, 3) − cos(0, 2)
=
0, 3 − 0, 2
≈ −0, 34273009
f [x0 , x1 ] =
Selisih terbagi orde ke-2,
f [x1 , x2 ] − f [x0 , x1 ]
x2 − x0
0, 3427550 − (−0, 2473009)
≈
0, 4 − 0, 2
= −0, 4772705
f [x0 , x1 , x2 ] =
Contoh 5.11
Gunakan semua titik-titik yang diberikan pada Tabel 5.6 untuk mengiterpolasi f (1, 5)
dengan menggunakan selisih terbagi Newton.
Penyelesaian:
Tabel 5.6 Nilai-nilai f (x) = ex
x
ex
1,0
1,3
1,6
1,9
2,2
0,7651977
0,6200860
0,4554022
0,2818186
0,1103623
Dengan menggunakan metode selisih terbagi Newton, diperoleh tabel sebagai berikut.
Bilangan-bilangan tebal pada tabel diatas merupakan koefisien dari polinom P4 (x).
Oleh karena itu, persamaan polinomnya adalah,
P4 (x) = 0, 7651977 − 0, 4837057(x − 1, 0) − 0, 1087339(x − 1, 0)(x − 1, 3)
+0, 0658784(x − 1, 0)(x − 1, 3)(x − 1, 6)
+0, 001825(x − 1, 0)(x − 1, 3)(x − 1, 6)(x − 1, 9)
106
Bab 5 Interpolasi
Tabel 5.7 Tabel Selisih Terbagi Newton orde 4
i
x
f [xi ]
ST1
0
1,0
0,7651977
1
1,3
0,6200860
2
1,6
0,4554022
3
1,9
0,2818186
ST2
ST3
ST4
-0,4837057
-0,1087339
-0,5489460
0,0658784
-0,0494433
-0,5786120
0,0018251
0,0680685
0,0118183
-0,5715210
4
2,2
0,1103623
Untuk x = 1, 5, maka
P4 (1, 5) = 0, 5118200
Latihan
5.2
1. Misalkan x0 = 0, 85, x1 = 0, 87, x2 = 0, 89 Dengan menggunakan Tabel 5.3 hitunglah
a. f [x0 , x1 ],
b. f [x1 , x2 ],
c. f [x0 , x1 , x2 ]
2. Hampiri fungsi f (x) = cos(x) dengan polinom interpolasi derajat tiga di dalam
selang[0, 0; 1, 2]. Gunakan empat titik x0 = 0, 0; x1 = 0, 4; x2 = 0, 8 dan x3 = 1, 2.
Perkirakan nilai P (0, 5) dan bandingkan nilai sejatinya.
3. Diberikan data di bawah ini, tentukan f [x0 , x1 ] dan f [x0 , x1 , x2 ]. Kemudian hitung
P1 (0, 15) dan P2 (0, 15)
n
0
1
2
xn
0,1
0,2
0,3
f (xn )
0,2
0,24
0,30
5.4 Galat Interpolasi Polinom
107
4. Diberikan data sebagai berikut. Tentukan f [x0 , x1 ] dan f [x0 , x1 , x2 ] dan kemudian
hitunglah P2 (0, 8) dan P2 (0, 9).
n
0
1
2
xn
0,5
1,0
2,0
f (xn )
0,479
0,841
0,909
5. Hitunglah P2 (7, 4) dan P3 (6, 5) dengan menggunakan data berikut.
n
0
1
2
3
5.4
xn
6,0
7,0
7,5
7,7
f (xn )
0,1506
0,3001
0,2663
0,2346
Galat Interpolasi Polinom
Polinom interpolasi Pn (x) merupakan hampiran terhadap fungsi yang asli f (x).
Pn (x) dan f (x) tidak sama, walaupun di titik-titik tertentu Pn (xi ) dan f (xi ) sama
untuk n = 0, 1, 2, . . . , n Oleh karena itu, muncul adanya galat diantara keduanya,yaitu
E(x) = f (x) − Pn (x)
(5.26)
Mengingat f (xi ) = Pn (xi ) untuk i = 0, 1, 2, . . . , n, maka harus berlaku juga,
E(xi ) = f (xi ) − Pn (xi ) = 0
(5.27)
E(x) dapat juga ditulis dalam bentuk,
E(x) = f (x) − Pn (x) = (x − x0 )(x − x1 ) · · · (x − xn )R(x)
atau
f (x) − Pn (x) − (x − x0 )(x − x1 ) · · · (x − xn )R(x) = 0
Dan galat dari interpolasi diberikan oleh,
E(x) = (x − x0 )(x − x1 ) · · · (x − xn )
atau
E(x) = Qn+1 (x)
f (n+1) (c)
(n + 1)!
f (n+1) (c)
(n + 1)!
(5.28)
(5.29)
108
Bab 4 Interpolasi
Rumus galat ini berlaku untuk semua metode interpolasi, baik interpolasi linear,
kuadratik, atau interpolasi dengan derajat lebih tinggi. Misalkan kita akan menginterpolasi dua titik dengan polinom Lagrange, maka galat interpolasinya adalah
E(x) =
5.5
(x − x0 )(x − x1 )
f ”(c)
2
(5.30)
Polinom Newton-Gregory
Pada pembahasan terdahulu telah kita pelajari tentang selisih terbagi Newton,
yang melibatkan selisih dua nila fungsi pada jarak yang sama. Polinom Newton-Gregory
merupakan kasus khusus dari polinom Newton untuk titik-titik yang berjarak sama dan
dilakukan pada selang waktu yang teratur.
Untuk titik-titik yang berjarak yang sama, rumus polinom Newton menjadi lebih
sederhana dan lebih mudah dibentuk dan tidak melibatkan pembagian pada proses
pembentukanya.
5.5.1
Polinom Newton-Gregory Maju
Misalkan terdapat x0 , x1 , x2 , . . . , xn yang merupakan nilai yang berjarak sama, maka
interpolasi Newton dapat dibentuk kembali menjadi ungkapan yang lebih sederhana.
Jika h = xi+1 − xi untuk i = 0, 1, 2, . . . , n − 1 dan x = x0 + sh, maka selisih x − xi dapat
ditulis kembali −xi = (s − i)h sehingga bentuk polinomial dapat juga ditulis,
P( x) = Pn (x0 + sh) = f [x0 ] + shf [x0 , x1 ] + s(s − 1)h2 f [x0 , x1 , x2 ]
= + · · · + s(s − 1) · · · (s − n + 1)hn f [x0 , x1 , . . . , xn ]
n
=
s(s − 1) · · · (s − k + 1)hk f [x0 , x1 , . . . , xk ]
k=0
Dengan menggunakan simbol binomial,
s
k
=
s(s − 1) · · · (s − k + 1)
k!
maka persamaan (5.31) dapat ditulis kembali menjadi,
Pn x = pn (x0 + sh) =
n
k=0
s
k
k!hk f [x0 , x1 , . . . , xk ]
(5.31)
4.5 Polinom Newton-Gregory
109
Dengan menggunakan simbol ∆ yang dikenalkan ole metode ∆2 Aitken,
f [x0 , x1 ] =
f [x0 , x1 , x2 ] =
f (x1 ) − f (x0 )
1
= ∆f (x0 )
x1 − x0
h
1 ∆f (x1 ) − ∆f (x0 )
1
= 2 ∆2 f (x0 )
2h
h
2h
secara umum ditulis,
f [x0 , x1 , . . . , xk ] =
1
∆2 f (x0 )
k!h2
(5.32)
Rumus Selisih maju Newton
Pn (x) =
n
k=0
s
k
∆k f (x0 )
(5.33)
Jika titik-titik di atur kembali dalam urutan mundur, xn , xn−1 , . . . , x0 , dengan menggunakan rumus polinomial Taylor memberikan,
Pn (x) = f [xn ] = f [xn−1 , xn ](x − xn ) + f [nn−2 , xn−1 , xn ](x − xn )(x−n−1 )
+ · · · + f [x0 , x1 , . . . , xn ](x − xn )(x − xn−1 ) · · · (x − x1 )
(5.34)
Dengan menggunakan jarak yang sama x = xn + sh dan x = xi + (s − n − i)h yang
menghasilkan
Pn (x) = Pn (xn + sh)
= f [xn ] + shf [xn−1 , xn ] + s(s + 1)h2 f [xn−2 , xn−1 , xn ] + · · ·
+s(s + 1) · · · (s + n − 1)hn f [x0 , x1 , . . . , xn ]
Bentuk ungkapan terakhir disebut rumus selisih terbagi mundur Newton.
Definisi 5.1
Diberikan barisan pn ∞
n=0 , mendefinisikan selisih mundur ∇pn oleh,
∇pn ≡ pn − pn−1 ,
n≥1
Untuk pangkat tinggi didefinisikan secara rekursif oleh,
∇k pn = ∇(∇k−1 pn ).
(5.35)
110
Bab 4 Interpolasi
Dari definisi di atas mengakibatkan
f [xn−1 , xn ] =
f [xn−2 , xn−1 , xn ] =
1
∇f (xn )
h
1 2
∇ f (xn )
2h2
dan secara umum ditulis,
f [xn−k , xn−k−1 , . . . , xn−2 , xn−1 , xn ] =
1
∇k f (xn )
k!hk
Jika bentuk di atas di masukan dalam bentuk polinomial Pn (x), maka akan memberikan
s(s + 1) 2
∇ f (xn ) + · · ·
2
s(s + 1)(s + 2) · · · (s + n − 1) n
∇ f (xn )
n!
Pn (x) = f [xn ] + s∇f (xn ) +
=
(5.36)
Jika kita misalkan,
−s
k
=
−s(−s − 1)(−s − 2) · · · (−s − k + 1)
k!
= (−1)k
s(s + 1) · · · (s + k − 1)
k!
(5.37)
dan
−s
1
Pn (x) = f (xn ) + (−1)1
n
+(−1)
−s
2
∇f (xn ) + (−1)2
∇2 f (xn )
−s
2
∇2 f (xn ) + · · ·
(5.38)
dan diperoleh rumus baku
Pn (x)
n
k=0
(−1)k
−s
k
∇k f (xn )
(5.39)
Contoh 5.12
Pertimbangkan tabel data berikut.
Jika kita akan menghampiri f (x) di x = 1, 1, sangat berasalan apabila kita
menggunakan x0 = 1, 0; x1 = 1, 3; x2 = 1, 6; x3 = 1, 9; x4 = 2, 2, paling tidak kita akan
gunakan data-data yang paling dekat dengan x = 1, 1, hal ini akan mengakibatkan
4.5 Polinom Newton-Gregory
111
Tabel 5.8 Tabel Selisih Terbagi Newton orde 4
x
f [xi ]
1,0
0, 7651977
1,3
0,6200860
ST1
ST2
−0, 4837057
0,4554022
0, 0658784
0,2818186
2,2
0, 1103623
0, 0018251
-0,0494433
-0,5786120
1,9
ST4
−0, 1087339
-0,5489460
1,6
ST3
0, 0680685
0, 0118183
−0, 5715210
h = 0, 3 dan s = 13 . Oleh karena itu, rumusan yang digunakan adalah selisih terbagi
Newton maju untuk data-data yang bergaris atas,
1
P4 (1, 1) = P4 1, 0) + (0, 3)
3
1
2
1
= 0, 7651997 + (0, 3)(−0, 4837057) +
−
(0, 3)2 (−0, 1087339)
3
3
3
2
5
1
−
−
(0, 3)3 (0, 0658784)
+
3
3
3
2
5
8
1
−
−
−
(0, 3)4 (0, 0018251)
+
3
3
3
3
= 0, 7196480
Ketika kita akan menghampiri f (2, 0), maka kita akan menggunakan data-data yang
paling dekat dengan x = 2, 0. Hal ini mengakibatkan h = 0, 3 dan s = − 23 . Oleh karena
itu, rumusan yang digunakan adalah selisih terbagi Newton mundur untuk data-data
yang bergaris bawah,
2
P4 (2, 0) = P4 (2, 2 − (0, 3))
3
2
2
= 0, 1103623 − (0, 3) (−0, 5715210) −
3
3
2 1
(0, 3)3 (0, 0680685)
−
3 4
4
7
2 1
(0, 3)4 (0, 0018251)
−
3 3
3
3
1
(0, 3)2 (0, 0118183)
3
112
Bab 4 Interpolasi
= 0, 2238754
Rumus Newton selisih terbagi, baik selisih terbagi maju maupun selisih terbagi
mundur tidak memperhatikan pendekatan nilai x.
Sebuah rumus selisih terbagi pusat, dengan memilih x0 yang dekat dengan titik
yang dihampiri dan kemudian tentukan secara langsung titik-titik dibawah x0 sebagai
x1 , x2 , x3 , . . . dan titik-titik di atas titik x − 0 sebagai x−1 , x−2 , . . .. Gunakan bentuk
tersebut, maka rumus Stirling diberikan oleh,
sh f [x−1 , x0 ] + f [x0 , x1 ]
2
s(s2 − 1)h3 +s2 h2 f [x−1 , x0 , x1 ] +
f [x−1 , x0 , x1 , x2 ] + f [x−2 , x−1 x0 , x1 ] + · · ·
2
+s2 (s2 − 1)(s2 − 4) · · · (s2 − (m − 1)2 )h2m f [x−m , x−m−1 , . . . , x0 , x1 , . . . , xm ]
s(s2 − 1) · · · (s2 − m2 )h2m+1 f [x−m , x−m−1 , . . . , x0 , . . . , xm+1 ]
2
(5.40)
+f [x−m−1 , . . . , x0 , . . . , xm ]
Pn (x) = P2m+1 (x) = f [x0 ] +
Jika n = 2m + 1 adalah ganjil, dan n = 2m adalah genap, maka hapus suku-suku
terakhir yang ditunjukkan pada Tabel 5.9.
Tabel 5.9 Selisih Terbagi Pusat Newton
x
f (x)
x−2
f [x0 ]
ST1
ST2
ST3
ST4
f [x0 , x1 ]
x−1
f [x1 ]
f [x0 , x1 , x2 ]
f [x1 , x2 ]
x0
f [x2 ]
f [x0 , x1 , x2 , x3 ]
f [x1 , x2 , x3 ]
f [x2 , x3 ]
x1
f [x3 ]
f [x0 , x1 , x2 , x3 , x4 ]
f [x1 , x2 , x3 , x4 ]
f [x2 , x3 , x4 ]
f [x3 , x4 ]
x2
f [x4 ]
Contoh 5.13
Gunakan rumusan selisih terbagi pusat orde ke-4 untuk menghampiri f (1, 5) dari datadata yang diberikan pada Tabel 5.10 berikut.
4.5 Polinom Newton-Gregory
113
Penyelesaian:
Untuk menghampiri f (x) di x = 1, 5, maka akan kita gunakan data-data yang lebih
Tabel 5.10 Tabel Selisih Terbagi Newton orde 4
x
f [xi ]
1,0
0,7651977
1,3
0,6200860
1,6
0,4554022
1,9
0,2818186
ST1
ST2
ST3
ST4
-0,4837057
-0,1087339
-0,5489460
0,0658784
-0,0494433
-0,5786120
0,0018251
0,0680685
0,0118183
-0,5715210
2,2
0,1103623
dekat ke x = 1, 5. Dari tabel jelas terlihat bahwa x = 1, 6 lebih dekat ke x = 1, 5.
Untuk itu x = 1, 6 di jadikan sebagai x0 , selanjutnya x−2 = 1, 0, x−1 = 1, 3, x1 = 1, 9
dan x2 = 2, 2. Dengan menggunakan rumusan Stirling, diperoleh h = 0, 3, x0 = 1, 6
dan s = − 13 , menjadi
1
(0, 3))
3
1
0, 3
(−0, 5489460) − 0, 5786120)
= 0, 4554022 + −
3
2
1
1
1 2
+
−
−
− 1 (0, 3)3 (0, 0658784 + 0, 0680685)
2
3
3
f (1, 5) ≈ P4 (1, 6 + −
1 2
+ −
3
= 0, 5118200
1
−
3
− 1 (0, 3)4 (0, 0018251)
114
Bab 4 Interpolasi
Latihan
5.3
1. Gunakan rumusan selisi terpusat untuk mengkontruksi interpolasi polinomial berderajat satu, dua, tiga dan empat dari data-data berikut.
a. f (8, 4), jika f (8) = 16, 63553, f (8, 1) = 17, 61549, f (8, 3) = 17, 56492,
f (8, 6) = 18, 50515, f (8, 7) = 18, 82091
b. f (0, 9) jika f (0, 5) = −0, 34409873, f (0, 6) = −0, 17694460, f (0, 7) = 0, 01375227,
f (0, 8) = 0, 22363362, f (1, 0) = 0, 65809197
2. Gunakan rumus selisih maju Newton untuk membuat interpolasi polinom derajat
satu, dua, tiga, dan tiga dari data-data berikut.
a. f (0, 25) jika f (0) = −1, f (0, 1) = −0, 62049958, f (0, 2) = 0, 28398668,
f (0, 3) = 0, 00660095, f (0, 4) = 0, 24842440
b. f (1, 15), jika f (1) = 1, 684370, f (1, 1) = 1, 949477, f (1, 2) = 2, 199796,
f (1, 3) = 2, 439189, f (1, 4) = 2, 670324
3. Gunakan rumus selisih mundur Newton untuk membuat interpolasi polinom derajat satu, dua, tiga, dan tiga dari data-data berikut.
a. f (0, 25) jika f (0) = −1, f (0, 1) = −0, 62049958, f (02) = −0, 28398668,
f (0, 3) = 0, 00660095, f (0, 4) = 0, 24842440
b. f (π/2) jika f (1, 1) = 1, 964760, f (1, 2) = 2, 572152, f (1, 3) = 3, 602102,
f (1, 4) = 5, 797884, f (1, 5) = 14, 10142
4. Gunakan selisih terbagi Newton untuk mengiterpolasi polinom dereajat empat
dari data pada tabel berikut.
xn
0,0
0,1
0,3
0,6
1,0
f (xn )
-6,00000
-5,89483
-5,65014
-5,17788
-4,28172
5.5 Interpolasi Splin
115
5. Hampiri f (0, 05) dengan menggunakan selisih terbagi maju Newton untuk data
yang diberikan pada tabel berikut.
x
f (x)
0,0
1,00000
0,2
1,22140
0,4
1,49182
0,6
1,82212
0,8
2,22554
a. Gunakan rumus selisih terbagi mundur Newton untuk f (0, 65)
b. Gunakan rumus Stirling untuk menghampiri f (0, 43)
6. Polinomial derajat empat P (x) memenuhi ∆4 P (0) = 24, ∆3 P (0) = 6, dan
∆2 P (0) = 0 di mana ∆P (x) = P (x + 1) − P (x). Hitunglah ∆2 P (10).
7. Diberikan data-data untuk polinomial P sebagai berikut .
x
P (x)
0
2
1
-1
2
4
jika semua selisih terbagi orde tiga adalah 1, hitunglah koefisien dari x2 pada P (x)
8. Diberikan data-data untuk polinomial P sebagai berikut.
x
P (x)
0
4
1
9
2
15
3
18
Jika semua selisih terbagi maju orde-4 adalah 1, hitunglah koefisien x3 pada polinomial P (x).
9. Diberikan
Pn (x) = f [x0 ] + f [x0 , x1 ](x − x0 ) + a2 (x − x0 )(x − x1 )
+a3 (x − x0 )(x − x1 )(x − x2 ) + · · ·
an (x − x0 )(x − x1 )(x − x2 ) · · · (x − xn−1 ).
Gunakan Pn (x2 ) untuk menunjukkan bahwa a2 = f [x0 , x1 , x2 ].
116
5.6
Bab 5 Interpolasi
Interpolasi Splin
Misalkan diberikan suatu data (nilai fungsi atau titik pada bidang xy), yaitu
(x0 , f0 ), (x1 , f (x1 )), . . . , (xn , f (xn )) yang dapat diinterpolasi oleh polinomial Pn (x) berderajat n atau lebih kecil sehingga kurva Pn (x) melalui n + 1 titik (xi , f (xi )). Untuk lebih
memahami definisi fungsi spline, akan kita mulai dengan persoalan interpolasi dari data
yang diberikan pada Tabel 5.11.
Tabel 5.11
x
0
1
2
2,5
3
3,5
4
y
2,5
0,5
0,5
1,5
1,5
1,125
0
Metode interpolasi yang paling sederhana adalah menghubungkan dengan garis
dari satu titik ke titik lainnya, sebagaimana ditunjukkan pada Gambar 5.6. Cara
seperti ini biasanya disebut Interpolasi linear sesepenggal. Fungsi-fungsi interpolasi
yang bersekutu dilambangkan dengan l(x)
Y
•
2
•
•
•
1
O
•
•
1
2
3
•
4
X
Gambar 5.6 y = l(x), interpolasi linear sesepenggal
Contoh 5.14
Pemilihan interpolasi berikutnya adalah menggunakan interpolasi polinomial. Terdapat
tujuh titik dan oleh karena itu, kita akan mempertimbangkan polinomial interpolasi
derajat enam, P6 (x), yang grafiknya ditunjukkan pada Gambar 5.8.
Pilihan ketiga adalah menghubungkan titik-titik tersebut dengan menggunakan
5.5 Interpolasi Splin
117
Y 6
4
3
2
1
O
1
2
3
4
X
-
Gambar 5.7 y = P6 (x), interpolasi linear derajat enam
interpolasi polinomial kuadratik. Sebut saja fungsi q(x) pada interval 0 ≤ x ≤ 4. Pada
setiap sub-interval [0, 2], [2, 3] dan [3, 4], q(x) adalah interpolasi polinomial kuadratik.
Y
6
r
2
r
r
r
1
O
r
r
1
2
3
X
r4
Gambar 5.8 y = q(x), interpolasi kuadratik sesepenggal
Untuk menyelesaikan masalah secara umum, misalkan terdapat n titik (xi , yi ),
dengan asumsi
x1 < x2 < · · · < xn
dan misalkan a = xi , b = xn . Kita akan menentukan sebuah fungsi dalam bentuk s(x)
yang terdefinisi pada [a, b] yang menginterpolasi data-data
s(xi ) = yi ,
i = 1, 2, 3, . . . , n
118
Bab 5 Interpolasi
Untuk lebih menghaluskan fungsi s(x), kita membutuhkan s (x) dan s (x) yang kontinu.
Pada persoalan ini, syarat adanya solusi s(x) yang unik jika memenuhi syaratsyarat sebagai berikut.
1. s(x) adalah polinomial kubik untuk setiap sub-interval [xj−1 , xj ], untuk j =
2, 3, . . . , n
2. s (x1 ) = s (xn ) = 0
Fungsi s(x) disebut f ungsisplinekubikalami yang menginterpolasi data-data (xi , yi ).
Kita akan memberikan sebuah metode untuk membangun s(x) dan kemudian menerapkannya terhadap tabel 5.11.
Misalkan diberikan variabel-variabel M1 , M2 , . . . , Mn dengan
Mi ≡ s (xi ),
i = 1, 2, . . . , n
Kita akan mengungkapkan s(x) ke dalam bentuk Mi yang tidak diketahui, dan kemudian
kita akan menghasilkan sebuah sistem persamaan linear dari Mi yang akan dihitung.
Oleh karena s(x) adalah kubik pada setiap interval [xj−1 , xj ], fungsi s (x) adalah
linear pada interval tersebut. Sebuah fungsi linear dihitung dengan menggunakan dua
titi, yaitu
s (xj−1 ) = Mj−1 ,
dan
s (x) =
s (xj ) = Mj
(xj − x)Mj−1 + (x − xj − 1)Mj
,
xj − x−1
xj−1 ≤ x ≤ xj
(5.41)
Selanjutnya kita akan membentuk antiderivatif orde-2 s (x) pada interval [xj−1 , xj ] dan
menerapkan syarat interpolasi
s(xj−1 ) = yj−1
Dengan memanipulasi, diperoleh polinomial kubik,
s(x) =
(xj − x)yj−1 + (x − xj−1 )yj
(xj − x)3 Mj−1 + (x − xj−1 )3 Mj
+
6(xj − xj−1 )
xj − xj−1
1
− (xj − xj−1 )[(xj − x)Mj−1 + (x − xj−1 )Mj ]
(5.42)
6
5.5 Interpolasi Splin
119
untuk xj−1 ≤ x ≤ xj . Rumusan spline 5.42 dihitung pada interval [x1 , x2 ], . . . , [xn−1 , xn ]
dan di set sedemkian rupa pada interval [xj−1 , xj ] dan [xj , xj+1 ] sehingga berhimpit
pada titik x = xj yang menyebabkan interpolasi s(xj ) = yj . Kondisi seperti ini akan
menyebabkan s(x) menjadi kontinu pada interval [a, b]. Dengan cara yang sama, rumusan pada 5.41 juga kontinu pada interval [a, b]. Oleh karena itu, s (x) uga kontinu pada
[a, b], dan rumusan s (x) pada [xj−1 , xj ] dan [xj , xj+1 ] dibutuhkan untuk menghitung
nilai-nilai pada titik x = xj untuk j = 2, 3, . . . , n − 2. Hasil terahir yang diperoleh
berupa sistem persamaan linear,
xj − xj−1
Mj−1 +
6
xj+1 − xj−1
xj+1 − xj
Mj +
Mj+1
3
6
yj+1 − yj
yj − yj−1
=
−
, j = 2, 3, . . . , n − 1
xj+1 − xj
xj − xj−1
(5.43)
Pada sistem persamaan linear 5.43, terdapat n−2 persamaan yang secara serentak akan
diselesaiakan dengan mengasumsikan bahwa,
M 1 = Mn = 0
(5.44)
Sistem persamaan linear 5.43 disebut sistem triagonal, dan terdapat sebuah metode
khusus untuk menyelesaikannya.
Contoh 5.15
Hitunglah interpolasi splin kubik alami berikut ini.
(1, 1), 2,
1
1
1
, 3,
, 4,
2
3
4
(5.45)
Dari contoh soal, diperoleh jumlah titik-titiknya adalah n = 4 dan untuk semua selisih
selang adalah x2 − x1 = x3 − x2 = x4 − x3 = 1. Berdasarkan sistem linear 5.43 dengan
j = 2, 3
Langkah awal untuk menyelesaikan persoalan ini adalah menentukan nilai Mj .
Oleh karena telah diasumsikan bahwa M1 = Mn = 0, maka M0 = M4 = 0. Selanjutnya
kita akan menghitung nilai Mj untuk j = 2, 3.
Untuk j = 2,
x2 − x1
x3 − x1
x3 − x2
M1 +
M2 +
M3 =
6
3
6
2
1
1
M1 + M2 + M 3 =
6
3
6
y 3 − y2
y2 − y1
−
x3 − x2 x2 − x1
1
3
(5.46)
120
Bab 5 Interpolasi
dan untuk j = 3,
x4 − x2
x4 − x3
x3 − x2
M2 +
M3 +
M4 =
6
3
6
2
1
1
M2 + M3 + M 4 =
6
3
6
y 4 − y3
y3 − y2
−
x4 − x3 x2 − x2
1
12
(5.47)
Oleh karena M1 = M4 = 0, maka persamaan (5.46) dan (5.47) menjadi,
2
M2 +
3
1
M2 +
6
1
M3 =
6
2
M3 =
3
1
3
1
12
(5.48)
(5.49)
Penyelesaian sistem persamaan liner dengan variabel tak diketahui M2 dan M3 . Dengan
menggunakan metode substitusi, diperoleh,
1
M2 = ,
2
M3 = 0
1
, M3 = 0 dan M4 = 0, ke dalam persamaan (5.42),
2
dan diperoleh sistem persamaan non linear,
Substisutikan nilai M1 = 0, M2 =
⎧
3
1 3 1 2 1
⎪
⎪
x
x
x
+
−
−
⎪
⎪
12
4
3
2
⎪
⎪
⎪
⎪
⎪
⎨
s(x) =
−
17
1 3 3 2 7
x = x − x+
12
4
3
6
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩ − 1 x+ 7
12
12
1≤x≤2
2≤x≤3
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
3≤x≤4 ⎭
(5.50)
5.5 Interpolasi Splin
121
Latihan
5.4
1. Kontruksi spline kubik untuk data-data berikut.
f (x)
17,56492
18,50515
a.
x
8,3
8,6
c.
x
−0, 5
−0, 25
0
e.
x
1,2
1,3
1,4
1,5
f (x)
−0, 0247500
0,3349375
1,1010000
x
b. 0,8
1,0
f (x)
0,22363362
0,65809197
x
3,0
d.
3,1
3,2
f (x)
−4, 240058
−3, 496909
−2, 596792
x
1,0
1,1
1,2
1,3
1,4
f (x)
2,572152
3,602102
5,797884
14,10142
f (x)
1,684370
1,949477
2,199796
2,439189
2,670324
2. Gunakan data-data pada soal no.1 untuk mengkontruksi spline kubik dan hampiri
f (x) dan f (x), hitung juga galat yang dihasilkan.
a. f (x) = x ln(x);, hampiri f (8, 4) dan f (8, 4)
b. f (x) sin(ex − 2); hampiri f (0, 9) dan f (0, 9)
c. f (x) = x cos x − 2x2 + 3x − 1; hampiri f (0, 25) dan f (0, 25)
d. f (x) = ln(ex − 2); hampiri f (1, 15) dan f (1, 15)
3. Diberikan data populasi penduduk (dalam ribuan) Amerika Seikat dari tahun 1940
sampai 1990.
Tahun
Penduduk
(dalam ribuan)
1940
1950
1960
1970
1980
1990
132.165
151.326
179.232
203.302
226.542
249.633
Gunakan interpolasi spline kubik untuk menghampiri populasi penduduk Amerika
Serikat pada tahun 1930, 1965, dan 2000.
122
Bab 5 Interpolasi
4. Sebuah kedaraan bergerak sepanjang jalan lurus dari suatu titik tertentu. Datadata pada tabel berikut diperoleh dari observasi di mana satuan waktu adalah detik (t), satuan jarak adalah meter (m), dan kecepatan adalah meter/detik (m/det).
Waktu
Jarak
Kecepatan
0
0
75
3
225
77
5
383
80
8
623
74
13
993
72
BAB 6
INTEGRASI NUMERIK
6.1
Pengertian dan Konsep Dasar
Di dalam kalkulus, integral merupakan salah satu cara untuk menentukan suatu
luasan di di bawah kurva y = f (x) yang dibatasi oleh x = a dan x = b. Menurut
teorema dasar kalkulus, jika F (x) adalah anti turunan f (x), maka integral f (x) dalam
interval [a, b] ditulis,
b
f (x)dx = F (x)
a
b
a
= F (b) − F (a)
(6.1)
Fungsi-fungsi yang dapat diintegralkan adalah fungsi-fungsi kontinu sederhana seperti
polinomial, eksponensial, atau trigonometri. Fungsi sederhana ini mudah dihitung integralnya secara eksak dengan menggunakan metode analitik. Metode-metode analitik
untuk menghitung fungsi tersebut sudah tersedia.
Y
y = f (x)
X
O
a
b
Gambar 6.1 Luasan daerah yang dibatas oleh kurva y = f (x) di dalam interval
[a, b].
124
Bab 6 Integrasi Numerik
Contoh 6.1
Berikut adalah beberapa rumusan untuk menghitung integral suatu fungsi.
axn+1
+C
(n + 1)
1
eax dx = (eax ) + C
a
1
dx = ln|x| + C
x
axn dx =
cot2 xdx = − cot x − x + C
Namun untuk fungsi-fungsi yang kompleks dan rumit, metode analitik kadang
tidak dapat menyelesaikan persoalan, oleh karena itu penyelesaiannya diperoleh dengan
menggunakan perhitungan secara numerik.
contoh
√
2
2 + cos(1 + x) 0,5x
e dx
0
1 + 0, 5 sin(x)
Persoalan integrasi numerik adalah menghitung f (x) secara numerik integral
tentu dalam interval [a, b],
b
I=
f (x)dx
(6.2)
a
Fungsi f (x) diberikan secara eksplisit dalam bentuk persamaan maupun secara
empirik dalam bentuk tabel nilai.
Terdapat tiga pendekatan dalam menurunkan rumus integrasi numerik. Pendekatan pertama adalah tafsiran geometri integral tentu. Daerah integrasi dibagi atas
sejumlah pias (strip) yang berbentuk segiempat. Luas daerah dihampiri dengan luas
seluruh pias. Integrasi yang diturunnkan dengan pendekatan demikian disebut metode
pias.
Pendekatan kedua adalah berdasarkan polinom interpolasi. Fungsi f (x) sebagai fungsi integran dihampiri dengan polinom interpolasi Pn (x). Oleh karena polinom
mudah diintegralkan, maka integrasi dilakukan terhadap polinom. Rumus integrasi
numerik yang diturunkan dengan pendekatan ini golongkan dalam metode NewtonCote.
Pendekatan yang ketiga, sama tidak menggunakan titik-titik diskrit untuk sebagaimana kedua pendekatan sebelumnya. Nilai integral diperoleh dengan mengevalu-
6.2 Metode Pias
125
asi nilai fungsi pada sejumlah titik-titik tertentu di dalam selang [−1, 1], mengalikannya dengan suatu konstanta, kemudian menjumlahkan keseluruhan perhitungan. Pendekatan demikian dinamakan Kuadratur Gauss.
6.2 Metode Pias
6.2.1 Kaidah Titik Tengah (Midpoint Rule)
Pandang sebuah pias berbentuk segi empat dengan panjang x = x0 dan x = x1 dan
titik tengah absis sebesar x = x0 + (x1 − x0 )/2, maka luas segi empat yang ditunjukkan
pada Gambar 6.2 adalah
x1 − x0
M (f ) = f x0 +
(x1 − x0 )
2
Jika lebar selang x1 − x0 = h, maka
h
M (f ) = f x0 +
h
2
sehingga luas daerah yang dibatas oleh fungsi f (x) pada interval [a, b] dapat diaproksimasi,
x1
x0
Y
f (x)dx ≈ f x0 +
h
h ≈ hf (x 1 )
2
2
(6.3)
6
y = f (x)
O
a = x0
ξ1
b = x1
X
-
Gambar 6.2 Luasan daerah yang dibatas oleh kurva y = f (x) di dalam interval
[a, b] dengan kaidah Titik Tengah dengan satu sub-interval
Gambar 6.2 menunjukkan aproksimasi luas pias terhadap fungsi f (x) pada interval [a, b]. Pendekatan luas yang dilakukan dengan cara tersebut biasanya disebut
126
Bab 6 Integrasi Numerik
aproksimasi dengan menggunakan metode pias, dan persamaan (6.3) di atas biasa disebut kaidah titik tengah. Jika selang [a, b] dibagi menjadi n buah pias, sehingga terdapat
x0 , x1 , x2 , . . . , xn , maka gabungan dari n pias adalah,
b
f (x)dx =
x1
x0
a
f (x)dx +
x2
x1
f (x)dx + · · · +
xn
f (x)dx
xn−1
h
3h
(2n − 1)h
h + f x0 +
h + · · · + f x0 +
h
≈ f x0 +
2
2
2
atau dapat kita tulis kembali menjadi,
b
a
f (x)dx ≈ f (ξ1 )h + f (ξ2 )h + · · · + f (ξn )h
= h
n
f (ξi )
(6.4)
i=0
dengan
ξi = x0 + (i − 1/2)h, dan i = 1, 2, 3, . . . , n
Y
6
y = f (x)
O
x0 ? x1 ? x2 ? x3 · · ·
ξ0
ξ1
ξ2
xn−1 ? xn
X
-
ξn−1
Gambar 6.3 Luasan daerah yang dibatas oleh kurva y = f (x) di [a, b] dengan
kaidah Titik Tengah
6.2.2
Kaidah Trapesium(Trapesium Rule)
Pada permulaan bab ini telah dijelaskan pengertian integral secara umum, yang pada
pada dasarnya merupakan integral Reimann, ditulis,
b
I(f ) =
f (x)dx
a
6.2 Metode Pias
127
Pada kaedah trapesium, metode yang dikembangkan merupakan pendekatan polinomial
linear, yaitu dengan menggunakan dua titik.
Pandang sebuah daerah yang dibatasi oleh fungsi f (x) dan interval [a, b] sebagaimana ditunjukkan pada Gambar 6.4. Misalkan, a = x0 dan b = x1 , maka luas daerah
yang di arsir adalah luas trapesium,
T (f ) =
=
I(f ) =
x1
x0
1
[f (x0 ) + f (x1 )](b − a)
2
b−a
[f (x0 ) + f (x − 1)]
2
f (x)dx ≈
(b − a)
[f (x0 ) + f (x1 )]
2
(6.5)
Y
y = f (x)
y = P1 (x)
X
O
a = x0
b = x1
Gambar 6.4 Luasan daerah yang dibatas oleh kurva y = f (x) pada interval
[a, b] dengan kaidah Trapesium.
Contoh 6.2
Aproksimasi dengan menggunakan kaedah Trapesium fungsi f (x) berikut pada interval
[0, 1],
1
I=
0
dx
1+x
Penyelesaian:
Dengan menggunakan persamaan (6.5), diperoleh
⎡
⎤
1 + 21
3
⎣
⎦ = = 0.75
T1 (f ) = (1 − 0)
2
4
128
Bab 6 Integrasi Numerik
Dari perhitungan secara eksak, diperoleh nilai I = log(2) = 0.75, sehingga galat yang
diperoleha adalah,
I − T1 ≈ −0, 0569
Untuk meningkatkan pendekatan yang lebih baik, maka selang atau interval [a, b] dipecahpecah menjadi sub-selang yang lebih kecil. Semakin banyak sub-selang, maka semakin
baik pendekatannya, sebagaimana ditunjukkan pada Gambar 6.5.
Y
y = f (x)
O
x2 · · · xn−1 b = xn
a = x0 x1
X
Gambar 6.5 Luasan daerah yang dibatas oleh kurva y = f (x) pada interval
[a, b] dengan n sub-interval.
Luas daerah dibawah kurva f (x) pada interval [a, b] merupakan luas hampiran
dari seluruh luas segiempat, sehingga
b
a
f (x)dx ≈
x1
x0
f (x)dx +
x2
f (x)dx +
x1
x3
x2
f (x)dx + · · · +
xn−1
f (x)dx
xn
h
h
[f (x0 ) + f (x1 )] + [f (x0 ) + f (x2 )]
2
1
h
+ · · · + [f (xn−1 ) + f (xn )]
2
h
[f (x0 ) + 2f (x1 ) + 2f (x2 ) + 2f (x3 ) + · · · + 2f (xn−1 ) + f (xn )]
=
2
n−1
h
=
f0 + 2
fi + fn
(6.6)
2
i=1
≈
Bentuk terakhir biasa disebut kaedah trapesium. Secara umum, galat diberikan oleh
1
E(f ) =
(n + 1)!
b
n
a
i=0
i=0
(x − xi )f (n+1) (ξ(x))dx
(6.7)
6.2 Metode Pias
129
Oleh karena kaedah trapesium menggunakan satu sub interval (n = 1), maka galat pada
interval a = x0 dan b = x1 adalah
E(f ) =
=
1 x1 f (ξ(x))(x − x0 )(x − x1 )dx
2 x0
x1
x1 1 (x − x0 )(x − x1 )dx = f (ξ)
x2 − (x0 + x1 ) + x1 x0 dx
f (ξ)
2
x0
x0
=
=
x1
x3 (x1 + x0 ) 2
1 f (ξ)
−
x + x0 x1 x
2
3
2
1 f (ξ)
2
x0
x31
(x1 + x0 ) 2
−
x1 + x0 x1 x1 −
3
2
x30 (x1 + x0 ) 2
−
x0 + x0 x1 x0
3
2
1 x1 (x1 + x0 )
x0 (x1 + x0 )
f (ξ) x21
−
+ x0 − x20
−
+ x1
=
2
3
2
3
2
1
h3
= =
− f (ξ)
2
6
= −
h3 f (ξ)
12
(6.8)
Oleh karena suku galat melibatkan f , maka galat akan menjadi nol (kaedah trapesium
menghasilkan nilai eksak) ketika fungsi f (x) bernilai nol pada turunan keduanya, yang
berarti fungsi f (x) adalah fungsi linear atau berorde lebih kecil.
Jika interval [a, b] dibagi menjadi n buah sub-interval dengan titik-titik a =
x0 , x1 , x2 , . . . , xn , maka galat yang terjadi adalah
Etot (f ) =
1
2
x1
x0
f (ξ(x))(x − x0 )(x − x1 )dx
1 x2 f (ξ(x))(x − x1 )(x − x2 )dx
+
2 x1
..
.
1 xn f (ξ(x))(x − xn−1 )(x − xn )dx
+
2 xn−1
h3
h3 f (ξ) + · · · + − f (ξ)
12
12
h3 = −n f (ξ)
12
= −
(6.9)
Oleh karena lebar sub-interval adalah h = (b − a)/n maka bentuk pada persamaan (6.9) dapat diubah menjadi,
Etot = −n
h3 f (ξ)
12
130
Bab 6 Integrasi Numerik
Tabel 6.1 Nilai-nilai f (xi ) untuk f (x) = ex dengan lebar sub-interval 0, 2
r
0
1
2
3
4
5
6
7
8
xi
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
f (xi )
6,050
7,389
9,025
11,023
13,464
16,445
20,086
24,533
29,964
= −n
b − a h3 12
(ξ)
n
f
h3
(b − a)f (ξ)
12
= O(h2 )
= −
(6.10)
Dari uraian di atas, diperoleh bahwa galat untuk n buah sub-interval dalam interval
[a, b] adalah,
b
a
n−1
h
f (x)dx =
f0 + 2
fi + fn O(h2 )
2
i=1
(6.11)
Galat total pada kaidah Trapesium sebanding dengan kuadrat lebar pias (h).
Jadi semakin kecil ukuran lebar sub-interval h, maka akan semakin kecil pula galatnya,
tetapi jumlah komputasinya semakin banyak.
Contoh 6.3
3,4
Hitung integral
1,8
ex dx dengan menggunakan kaedah trapesium dengan h = 0, 2 den-
gan mengambil 5 digit penting
Penyelesaian:
Jumlah pias n = (b − a)/h = (3, 4 − 1, 8)/0, 2 = 8
Nilai-nilai dari setiap xi ditunjukkan pada Tabel 6.1.
6.3 Metode Newton-Cotes
131
Nilai integrasinya adalah
3,4
1,8
h
[(f0 + 2f1 + 2f2 + · · · + 2f6 + 2f7 + 2f8 ]
2
0, 2
[6, 050 + 2(7, 389) + 2(9, 025) + · · · + 2(24, 533) + 29, 964]
≈
2
≈ 23, 994
(6.12)
dx ≈
sedangkan nilai integrasi sejatinya adalah
3,4
1,8
ex dx =
ex
x=3,4
x=1,8
= e3,4 − e1,8
= 23, 914
Galat kaidah trapesium,
E=−
h2
(b − a)f ”(t),
12
1, 8 < t < 3, 4
Oleh karena f (x) = ex dan f ”(x) = ex , maka
E=−
0, 22
(3, 4 − 1, 8)et ,
12
1, 8 < t < 3, 4
Karena fungsi f (x) = ex adalah fungsi yang menaik secara monoton di dalam
selang [1, 8; 3, 4], maka batas-batas galatnya ditentukan sebagai berikut,
E=−
6.3
⎧ 1,8
⎪
⎨ e (min) = −0, 0323(min)
1
(0, 2)2 (3, 4 − 1, 8)
⎪
12
⎩
e3,4 (maks) = −0, 1598(maks)
Metode Newton-Cotes
Metode N ewton − Cotes adalah metode yang paling umum digunakan untuk
menurunkan kaidah integrasi numerik, yang mana ide dasarnya adalah penggunaan
polinom Pn (x) untuk menghampiri fungsi f (x),
b
I=
a
f (x)dx ≈
b
a
Pn (x)dx
dengan
Pn (x) = a0 + a1 (x) + a2 x2 + · · · + an−1 xn−1 + an xn
(6.13)
132
Bab 6 Integrasi Numerik
Polinom yang digunakan dalam pembahasan ini adalah polinom Newton-gregory maju
yang ditulis dalam bentuk,
∆f0
∆2 f0
+ (x − x0 )(x − x1 )
+ ···
!!h
2!h2
∆n f0
+(x − x0 )(x − x1 ) . . . (x − xn−1 )
n!hn
Pn (x) = f0 + (x − x0 )
6.3.1
Kaidah Trapesium
Jika diberikan dua buah titik (0, f (x)) dan (h, f (h). Polinom interpoalasi yang melalui
dua titik adalah sebuah garis lurus. Luas daerah yang dihitung sebagai hampiran nilai
integrasi adalah daerah di bawah garis lurus tersebut (Gambar ??).
Y
y = f (x)
y = P1 (x)
X
O
a = x0
b = x1
Gambar 6.6 Pendekatan Polinom P1 (x) terhadap Luasan daerah yang dibatas
oleh kurva y = f (x) di dalam interval [0, h] dengan Kaidah Trapesium
Integrasi P1 (x) pada interval [0,h]adalah
I≈
0 f (x)dx ≈
h
≈
≈
≈
≈
h
P1 (x)dx
h
∆f0
f0 + x
dx
h
0
x=h
x2
∆f0 xf0 +
x=0
2h
h
hf0 + ∆f0
2
h
hf0 + (f1 − f0 )
2
6.3 Metode Newton-Cotes
133
≈
h
(f0 + f1 )
2
Jadi kaidah trapesium adalah,
h
0
f (x)dx ≈
h
(f0 + f1 )
2
(6.14)
sedangkan galatnya adalah
E=−
1 3
h f ”(t) = O(h3 ),
12
0<t<h
Untuk n buah pias, maka luas integrasi y = f (x) yang didekati polinom Pn (x)
dalam interval [a, b] diperoleh dengan menjumlahkan setiap hasil hampiran pada setiap
sub-interval [x0 , x1 ], [x1 , x2 ], . . . , [xn−1 , xn ], sehingga jumlah luas trapesium adalah
b
a
f (x)dx ≈
≈
≈
≈
6.3.2
x1
f (x)dx +
x0
x2
x1
f (x)dx +
x3
x2
f (x)dx + · · · +
xn
f (x)dx
xn−1
h
h
h
h
(f0 + f1 ) + (f1 + f2 ) + (f2 + f3 ) + · · · + (fn−1 + fn )
2
2
2
2
h
(f0 + 2f1 + 2f2 + · · · + 2fn−1 + fn )
2
n−1
h
f0 + 2
f i + fn
(6.15)
2
i=1
Kaedah Simpson 1/3
Pada kaedah trapesium, polinomial yang digunakan untuk mendekati nilai sejati adalah
polinomial linear, yaitu dengan menggunakan dua titik. Berdasarkan teori polinomial
yang telah dibahas pada bab sebelumnya, semakin banyak titik yang digunakan untuk
pedekatan, maka hasilnya akan semakin akurat. Untuk itu, berikut ini akan digunakan
pendekatan polinomial kuadratik, yaitu dengan menggunakan tiga titik yang berjarak
sama.
Misalkan suatu fungsi f (x) kontinu pada interval [a, b]. Jika terdapat titik c
yang membagi sama besar [a, b], dengan c = (a + b)/2, maka dengan menggunakan
interpolasi kuadratik diperoleh,
P2 (x) =
(x − a)(x − b)
(x − a)(x − c)
(x − c)(x − b)
f (a) +
f (c) +
f (b)
(a − c)(a − b)
(c − a)(c − b)
(b − a)(b − c)
(6.16)
134
Bab 6 Integrasi Numerik
sehingga
b
I(f ) =
a
f (x) ≈
=
b
P2 (x)dx
a
b
(x − c)(x
(x − a)(x − b)
− b)
f (a) +
f (c)
(a − c)(a − b)
(c − a)(c − b)
a
(x − a)(x − c)
f (b) dx
+
(b − a)(b − c)
(6.17)
Selanjutnya, kita akan mengevaluasi setiap sukunya. Jika lebar selang h =
(b − a)/2, maka b = a + 2h, (a − c) = −h dan (a − b) = −2h. Dengan mengambil
u = x − a, maka suku pertama dapat diubah dalam bentuk,
b
(x − c)(x − b)
a
(a − c)(a − b)
dx =
=
a+2h
1
(x − (a + h))(x − (a + 2h))dx
(−h)(−2h) a
a+2h
1
(u − h)(u − 2h)du
(−h)(−2h) a
=
1 u3 3 2
− u h + 2h2 u
2h2 3
2
=
h
3
2h
0
(6.18)
Untuk suku ke dua,
b
(x − a)(x − b)
a
(c − a)(c − b)
dx =
=
a+2h
1
(x − a)(x − (a + 2h))dx
(h)(−h) a
a+2h
1
u(u − 2h)du
−h2 a
=
=
=
2h
1 1 3
u − u2 h
−h2 3
1 −4 3
h
−h2 3
4
h
3
0
(6.19)
Untuk suku ketiga,
b
(x − a)(x − c)
a
(b − a)(b − c)
dx =
=
a+2h
1
(x − a)(x − (a + h))dx
(2h)(h) a
a+2h
1
u(u − h)du
2h2 a
=
2h
1 1 3 1 2
u − u h
2h2 3
2
0
6.3 Metode Newton-Cotes
135
=
=
2 3
h
3
1
2h2
h
3
(6.20)
Dari hasil evaluasi suku tersebut, maka persamaan (6.17) menjadi,
b
S2 (f ) =
a
P2 (x)dx =
h
f (a) + 4f
3
a+b
2
+ f (b)
(6.21)
Hasil lengkap dari persamaan terakir ditunjukkan pada Gambar 6.7. Jika interval [a, b]
Y
y = P2 (x)
y = f (x)
X
a
O
(a + b)/2
b
Gambar 6.7 Pendekatan Polinom P2 (x) terhadap Luasan daerah yang dibatas
oleh kurva y = f (x) di dalam interval [0, h] dengan kaedah Simpson 1/3
dibagi menjadi n sub interval dengan titik-titik a = x0 , x1 , x2 , . . . , xn = b, dan evaluasi
setiap tiga titik diberikan oleh,
x2
x2
h
f (x0 ) + 4f( x1 ) + f (x2 )
3
x0
x0
x4
x4
h
f (x)dx ≈
P2 (x)dx =
f (x2 ) + 4f( x3 ) + f (x4 )
3
x2
x2
..
.
xn
xn
h
f (x)dx ≈
P2 (x)dx =
f (xn−2 ) + 4f( xn−1 ) + f (xn )
3
xn−2
xn−2
f (x)dx ≈
P2 (x)dx =
b
I(f ) =
f (x)dx =
xn
a
=
x2
x0
f (x)dx
x
f (x)dx +
0 x4
x2
f (x)dx + · · · +
xn
xn−2
f (x)dx
136
Bab 6 Integrasi Numerik
h
f (x0 ) + 4f (x1 ) + 2f (x2 ) + 4f (x3 ) + 2f (x4 )
3
+ · · · + 2f (xn−2 ) + 4f (xn−1 ) + f (xn )
Sn (f ) =
(6.22)
Metode Simpson 1/3 diperoleh dengan mengintegralkan polinomial kuadratik, yaitu
menggunakan tiga titik. Jika polinomial P2 (x) diintegralkan pada interval a = x0 dan
b = x2 , dan terdapat x1 yang membagi interval menjadi dua sub-interval sama besar.
Oleh karena metode simpson 1/3 menggunakan dua sub-interval (n = 2), maka galat
simpson yang dihasilkan dapat diperoleh dengan menggunakan pendekatan polinomial
Taylor.
Misalkan f (x) diekspansi oleh polinomial Taylor orde ketiga terhadap x1 , dan
untuk setiap x pada [x0 , x2 ] terdapat sebuah bilangan ζ di dalam (x0 , x) sehingga
f (x) = f (x1 ) + f (x1 )(x − x1 ) +
+
f (x1 )
f (x1 )
(x − x1 )2 +
(x − x1 )3
2
6
f (4) (ζ(x))
(x − x1 )4
24
(6.23)
Bentuk integral dari persamaan diatas dapat ditulis,
x2
x0
f (x)dx = f (x1 )(x2 − x0 ) +
f (x1 )
(x − x1 )4
+
24
f (x1 )
f (x1 )
(x − x1 )2 +
(x − x1 )3
2
6
x2
x0
1
+
24
x2
x0
f (4) (ζ(x))(x − x1 )4 dx (6.24)
Oleh karena bentuk (x − x1 )4 tidak pernah negatif pada iterval [x0 , x2 ],maka menurut
teorema nilai rata-rata menyebabkan integral suku terakhir,
1
24
x2
x0
f
(4)
4
(ζ(x))(x − x1 ) dx =
=
f (4) (ζ)
24
x2
x0
(x − x1 )4 dx
f (4) (ζ)
(x − x1 )5
120
x2
(6.25)
x0
Oleh karena h = x2 − x1 = x1 − x0 , maka
(x2 − x1 )2 − (x0 − x1 )2 = (x2 − x1 )4 − (x0 − x1 )4 = 0,
(x2 − x1 )3 − (x0 − x1 )3 = h3 − (−h3 ) = 2h3 ,
(x2 − x1 )5 − (x0 − x1 )5 = h5 − (−h5 ) = 2h5
dan
6.3 Metode Newton-Cotes
137
Akibatnya, persamaan (6.24) dapat ditulis kembali menjadi,
x2
x0
Jika kita gantikan
f (x1 )
f (x)dx = 2hf (x1 ) +
h3 f (4) 5
f (x1 ) +
h
3
60
dengan pendekatan yang diberikan sub-bab sebelumnya, maka
kaedah Simspon diberikan oleh,
x2
f (x)dx =
x0
h
h5
f (x0 ) + 4f (x1 ) + f (x2 ) − f (4) (ζ)
3
90
(6.26)
Jika selang [a, b] dibagi menjadi n selang dan evaluasi kaedah Simpson 1/3 membutuhkan 2 buah selang, maka terdapat n/2 evaluasi kaedah Simspon, sehingga galat
totalnya adalah jumlahd dari galat-galat pada selang [x0 , x2 ], [x2 , x4 ], . . . , [xn−2 , xn ],
h5 (4)
f (ζ),
90 0
h5 (4)
= − f2 (ζ)
90
E0 = −
E2
..
.
En−2 = −
h5 (4)
f
(ζ)
90 n−2
dan galat totalnya,
Etot = E0 + E2 + E4 + · · · + En−2
h5 (4)
h5 (4)
h5 (4)
= − f0 (ζ) − f2 (ζ) − · · · − fn−2 (ζ)
90
90
90
h5 (4)
(4)
(4)
= −
f0 (ζ) + f2 (ζ) + · · · + fn−2 (ζ)
90
h5 n−2
(4)
= −
f (ζ)
90 i=0,2,4... i
h5 n
f (4) (ζ), a < ζ < b dan n = (b − a)/h
90 2
h4
(b − a)f (4) (ζ)
= −
180
= −
6.3.3
(6.27)
Kaedah Simpson 3/8
Pada sub-bab terdahulu. kita telah menurunkan formulasi kaedah Simpson 1/3. Selanjutnya, kita akan menentukan formulasi kaedah Simpson 3/8 yang menggunakan empat
titik, yaitu pendekatan polinomial kubik.
138
Bab 6 Integrasi Numerik
Misalkan sebua fungsi f (x) yang didekati oleh polinomial kubik P3 (x) yang
menggunakan empat titik berjarak sama, yaitu x0 , x1 , x2 , x3 dan polinomialnya adalah,
P3 (x) =
(x − x1 )(x − x2 )(x − x3 )
f (x0 ) +
(x0 − x1 )(x0 − x2 )(x0 − x3 )
(x − x0 )(x − x1 )(x − x3 )
f (x2 ) +
(x2 − x0 )(x2 − x1 )(x2 − x3 )
(x − x0 )(x − x2 )(x − x3 )
f (x1 )
(x1 − x0 )(x1 − x2 )(x1 − x3 )
(x − x0 )(x − x1 )(x − x2 )
f (x3 )
(x3 − x0 )(x3 − x1 )(x3 − x2 )
(6.28)
Selanjutnya kita akan hitung luas daerah pada [x0 , x3 ] dengan menggunakan polinomial
kubik P3 (x),
x3
I(f ) =
x
x0 3
≈
x0
x3
f (x)dx
P3 (x)dx
(x − x1 )(x − x2 )(x − x3 )
f (x0 )
(x
x0
0 − x1 )(x0 − x2 )(x0 − x3 )
x3
(x − x0 )(x − x2 )(x − x3 )
f (x1 )
+
x0 (x1 − x0 )(x1 − x2 )(x1 − x3 )
x3
(x − x0 )(x − x1 )(x − x3 )
f (x2 )
=
(x
x0
2 − x0 )(x2 − x1 )(x2 − x3 )
x3
(x − x0 )(x − x1 )(x − x2 )
f (x3 )
+
x0 (x3 − x0 )(x3 − x1 )(x3 − x2 )
=
(6.29)
Dengan cara yang sama seperti penurunan kaedah Simpson 1/3, maka diperoleh,
I(f ) =
x3
x0
f (x)dx ≈
3h
f (x0 ) + 3f (x1 ) + 3f (x2 ) + f (x3 )
8
(6.30)
Jika interval [a, b] dibagi menjadi n sub-interval dan n adalah kelipatan 3, maka luas
gabungan dengan menggunakan kaedah Simpson 3/8 adalah,
b
In (f ) =
a
f (x)dx ≈
x3
x0
f (x)dx +
x6
f (x)dx +
x3
x6
x3
f (x)dx + · · · +
xn
f (x)dx
xn−3
3h
f (x0 ) + 3f (x1 ) + 3f (x2 ) + f (x3 )
8
3h
+
f (x3 ) + 3f (x4 ) + 3f (x5 ) + f (x6 )
8
3h
+··· +
f (xn−3 ) + 3f (xn−2 ) + 3f (xn−1 ) + f (xn )
8
n−1
n−3
3h =
f (x0 ) + 3
fi (x) + 2
fi (x) + fn (x)
(6.31)
8
i=1
i=3,6,9,...
=
i=3,6,9,...
6.3 Metode Newton-Cotes
139
Sedangkan galat yang dihasilkan pada setiap evaluasi interpolasi polinomial kubik P3 (x)
adalah,
E=−
3 5 (4)
h f (ζ),
80
0 < ζ < 3h
(6.32)
Jika interval [a, b] di bagi menjadi n sub-interval yang merupakan kelipatan 3, maka
galat gabungan adalah
Etot = E1 + E2 + · · · + En/3
3
3
3
3
(4)
(4)
(4)
(4)
= − h5 f1 (ζ) − h5 f2 (ζ) − h5 f3 (ζ) − · · · − h5 fn/3 (ζ)
80
80
80
80
=
n/3 n/3
3h5 (4)
−3h5 (4)
f (ζ) = −
f (ζ)
i=1
80
80
3h5
3h5
i=1
n (4)
(b − a) (4)
= −
f (ζ) = −
f (ζ)
80 3
80
h
(b − a)h4 (4)
= −
f (ζ), a < ζ < b
80
(6.33)
6.3.4
Kaedah Boole
Kaedah Boole menggunakan 4 sub-interval untuk mengevaluasi luas dibawah kurva.
Untuk itu, polinom yang digunakan adalah interpolasi polinom derajat 4.
Misalkan sebua fungsi f (x) yang didekati oleh polinomial kubik P4 (x) yang
menggunakan empat titik berjarak sama, yaitu x0 , x1 , x2 , x3 , x4 dan polinomialnya adalah,
P3 (x) =
(x − x1 )(x − x2 )(x − x3 )(x − x4 )
f (x0 )
(x0 − x1 )(x0 − x2 )(x0 − x3 )(x0 − x4 )
(x − x0 )(x − x2 )(x − x3 )(x − x4 )
f (x1 )
+
(x1 − x0 )(x1 − x2 )(x1 − x3 )(x1 − x4 )
..
.
(x − x0 )(x − x1 )(x − x2 )(x − x4 )
f (x3 )
+
(x3 − x0 )(x3 − x1 )(x3 − x2 )(x3 − x4 )
(x − x0 )(x − x1 )(x − x2 )(x − x3 )
f (x4 )
+
(x4 − x0 )(x4 − x1 )(x4 − x2 )(x4 − x3 )
sehingga
x4
x0
f (x)dx ≈
x4
x0
P4 (x)dx
(6.34)
140
Bab 6 Integrasi Numerik
x4
=
x0
..
.
+
(x − x1 )(x − x2 )(x − x3 )(x − x4 )
f (x0 )dx
(x0 − x1 )(x0 − x2 )(x0 − x3 )(x0 − x4 )
x4
x0
(x − x0 )(x − x1 )(x − x2 )(x − x3 )
f (x4 )dx
(x4 − x0 )(x4 − x1 )(x4 − x2 )(x4 − x3 )
(6.35)
Dengan cara yang sama diperoleh,
x4
x0
f (x)dx ≈
2h
(7f (x0 ) + 32f (x1 ) + 12f (x2 ) + 32f (x3 ) + 7f (x4 ))
45
(6.36)
Persamaan (6.36) disebut kaedah Boole. Jika interval [a, b] dibagi menjadi n subinterval yang mana n merupakan kelipatan 4, maka kaedah Boole gabungan dituliskan
sebagai berikut.
b
f (x)dx =
x4
a
f (x)dx +
x0
≈
x8
x4
f (x)dx + · · · +
xn
f (x)dx
xn−4
2h
7f (x0 ) + 32f (x1 ) + 12f (x2 ) + 32f (x3 ) + 7f (x4 )
45
2h
+
7f (x4 ) + 32f (x5 ) + 12f (x6 ) + 32f (x7 ) + 7f (x8 )
45
..
.
2h
7f (xn−4 ) + 32f (xn−3 ) + 12f (xn−2 ) + 32f (xn−1 ) + 7f (xn )
45
=
n−1
n−2
2h
7f (x0 ) + 2 32
f (xi ) + 12
f (xi )
45
i=1,3,5,...
i=2,6,10,...
n−4
+7
f (xi ) + 7f (xn )
(6.37)
i=4,8,12,...
Latihan
6.1
1. Hampiri integral berikut dengan menggunakan aturan Trapesium.
1,5
a.
c.
e.
g.
x2 ln xdx
10,35
0π/4
0 3,5
3
x2
3x
e
√
1
b.
2
dx
−4
d.
sin 2xdx
f.
x
dx
−4
h.
x2
0
x2 e−x dx
π/4
01,6
x2 sin xdx
2x
dx
−4
2
1 π/4x
0
cos2 xdx
6.3 Metode Newton-Cotes
141
2. Hampiri integral-integral berikut dengan menggunakan kaedah trapesium, simpson, simpson 3/8 dan titik tengah. Bandingan dari kaedah-kaedah tersebut, manakah yang lebih baik.
0,1 √
a.
1 + xdx
05,5
c.
1,1
1
dx +
x
10
1
x
5,5
π/2
b.
dx
01
f.
0
(sin x)2 dx
x1/3 dx
3. Gunakan aturan Trapesium gabungan dengan n yang diberikan untuk menghampiri integral-integral berikut.
2
a.
c.
e.
g.
12
0
2
0 5
3
x ln xdx,
x2
n=4
2
dx,
+4
1
x2
−4
dx,
0
d.
n=8
f.
n=8
h.
2
4. Untuk mendekati
b.
n=6
e2x sin 3xdx,
√
−2
π
0
3
x3 ex dx,
x2 cos xdx,
x
x2 +
1 3π/8
0
n=4
4
dx,
n=6
n=8
tan xdx,
n=8
2
x2 e−x dx, dengan menggunakan
a. aturan trapesium gabungan dengan n = 8
b. aturan simpson gabungan dengan n = 8
c. aturan titik tengah gabungan dengan n = 8
5. Hitunglah niai n dan h yang diperlukan untuk menghampiri
2
0
dengan
10−4 ,
e2x sin 3xdx
dengan menggunakan:
a. aturan trapesium gabungan
c. aturan titik tengah gabungan
b. aturan simpson gabungan
6. Ulangan soal di atas untuk integral
π
0
x2 cos xdx
7. Hitunglah nilai n dan h yang diperlukan untuk menghampiri,
2
0
1
dx
x+4
142
Bab 6 Integrasi Numerik
dalam 10−5 dengan menggunakan:
a. aturan trapesium komposit
c. aturan titik tengah komposit
b. aturan simpson komposit
8. Persamaan
x
0
1
2
√ e−t /2 dt − 0, 45
2π
dan
1
2
f (x) = √ e−x /2 .
2π
Untuk mengevaluasi pada pendekatan pk , kita membutuhkan rumus kuadratur
untuk menghampiri,
pk
0
1
2
√ e−t /2 dt
2π
a. Tentukan sebuah solusi f (x) = 0 dengan akurasi 10−5 dan gunakan metode
Newton untuk p0 = 0, 5 dan aturan Simpson gabungan
b. Ulangan soal (a) dengan menggunakan aturan trapesium gabungan dan kemudian bandingan dengan aturan Simpson gabungan
6.4
Penggunaan Ekstrapolasi
Beberapa metode telah dipelajari untuk mendekati luas suatu daerah yang
menggunakan lebar sub-interval sama, h. Berdasarkan teori, luas pendekatan suatu
daerah akan bernilai eksak jika h = 0. Untuk itu, agar luas yang dihasilkan lebih baik,
salah satu cara yang digunakan adalah dengan memperkecil nilai h, atau ekstrapolasi
h = 0.
6.4.1
Ekstrapolasi Richardson
Pandang kembali kaedah trapesium,
b
I(f ) =
a
n
h
(b − a)f (ζ) 2
h
f (x)dx =
f0 + 2
fi + fn −
2
12
i=1
(6.38)
atau dapat ditulis sebagai
I(f ) = I(h) + ch2
(6.39)
143
6.4 Penggunaan Ekstrapolasi
dengan I(f ) adalah nilai integrasi sebenarnya, I(h) adalah nilai integrasi kaedah Trape(b − a)f (ζ) 2
sium dengan lebar selang h, dan c = −
h . Secara umum dapat ditulis,
12
If = Ih + chp
(6.40)
dengan c dan p adalah konstanta yang tidak bergantung kepada h. Nilai p dapat ditentukan langsung dari orde galat kaidah integrasi, misalnya, kaedah trapesium (O(h2 )),
maka p = 2, kaedah titik tengah (O(h2 )), maka p = 2, dan kaedah Simpson 1/3 (O(h4 )),
maka p = 4.
Ekstrapolasi Ricahrdson dilakukan untuk menghitung nilai integrasi yang lebih
baik dibandingkan dengan I.
Misalkan If adalah nilai integrasi yang lebih baik daripada Ih dengan jarak h,
maka
If = Ih + chp
(6.41)
Selanjutnya ekstrapolasi h menjadi 2h,maka integrasi numeriknya adalah,
If = I2h + c(2h)p
(6.42)
Dengan menghilang If pada persamaan (6.41) dan (6.42) diperoleh,
Ih + chp = I2h + c(2h)p
Ih + chp = I2h + c2p hp
Ih − I2h
c =
(2p − 1) hp
(6.43)
Sulihkan persamaan (6.43) ke dalam persamaan (6.41), dan diperoleh
If
Ih − I2h
= Ih +
hp
(2p − 1) hp
Ih − I2h
= Ih + p
2 −1
(6.44)
Ih − I2h
2p − 1
disebut faktor koreksi. Adanya faktor koreksi pada ekstrapolasi Richardson mempenPersamaan (??) disebut persamaan Ekstrapolasi Richardson, dan bentuk
garuhi nilai integrasi yang dihasilkan.
Kaedah trapesium yang digunakan untuk menghitung Ih dan I −2h dengan orde
galat p = 2, maka ekstrapolasi Richardson adalah,
1
If = Ih + [Ih − I2 h]
3
(6.45)
144
Bab 6 Integrasi Numerik
sedangkan untuk kaedah Simpson dengan orde galat p = 4, maka ekstrapolasi Richardsonnya adalah,
If = Ih +
1
[Ih − I2 h]
15
(6.46)
Perhatikan bahwa dari kedua kaedah yang digunakan, menunjukkan bahwa faktor koreksi pada kaedah Simspon lebih baik. Fakta ini menunjukkan bahwa orde galat pada
suatu kaedah memberikan pengaru terhadap faktor koreksi, dan nilai integrasi dapat
ditingkatkan dengan menambahkan faktor koreksi.
Contoh 6.4
Hitung kembali integral
1
0
1
dx
1+x
dengan menggunakan ekstrapolasi Richardson untuk kaedah trapesium dan h = 0, 125.
Penyelesaian:
Oleh karena h = 0, 125, maka jumlah sub-interval n = (1 − 0)/0, 125 = 8
Tabel 6.2 Nilai-nilai dari kaedah Trapesium
i
xi
fi
0
1
2
3
4
5
6
7
8
0
0,125
0,250
0,375
0,500
0,625
0,750
0,875
1,000
1
0,88889
0,80000
0,72727
0,66667
0,61538
0,57143
0,53333
0,50000
Dari tabel di atas dapat ditentukan nilai integrasi dengan kaedah trapesium
untuk h = 0, 125, yaitu
Ih =
7
h
f0 + 2
fi + f8
2
i=1
145
6.4 Penggunaan Ekstrapolasi
0, 125 1 + 2(0, 88889 + 0, 80000 + · · · + 0, 53333) + 0, 50000
2
= 0, 69412
=
sedangkan nilai integrasi dengan kaedah trapesium untuk 2h = 0, 250, yaitu
I2h =
3
2h
f0 + 2
f2i + f8
2
i=1
0, 125 1 + 2(0, 80000 + 0, 66667 + 0, 57143) + 0, 50000
2
= 0, 69702
=
Selanjutnya akan ditentukan nilai integrasi dengan menggunakan ekstrapolasi Richardson. Oleh karena orde galat dari kaedah trapesium adalah 2, maka rumusan ekstrapolasi
Richardson adalah
If
1
= Ih + (Ih − I2h )
3
1
= 0, 69412 + (0, 69412 − 0, 69702)
3
= 0, 69315
Sekarang kita bandingkan dengan nilai sejatinya,
1
0
1
dx = ln(1 + x)
1+x
1
0
= ln 2 − ln 1 = 0, 69314718
Jika kita ambila 5 angka dibelakang koma, maka
1
0
1
dx = 0, 69315
1+x
Dari hasil pembulatan nilai sejatinya, ternyata nilai integrasi ekstrapolasi Richardson
tepat sama dengan nilai sejatinya.
6.4.2
Ekstrapolasi Aitken
Ekstrapolasi Aitken muncul karena terdapat persoalan yang ditemukan pada ekstrapolasi, sehingga ekstrapolasi Richardson tidak dapat digunakan.
Pada ekstapolasi Richardson melibatkan orde galat dari suatu kaedah yang digunakan. Selanjutnya timbul masalah, bagaimana kalau orde galat tidak diketahui?
146
Bab 6 Integrasi Numerik
Untuk itu, kita akan menghilangkan orde galat p dan kita akan menggunakan tiga buah
nilai perkiraan integrasi, yaitu Ih , I2h dan I4h , sehingga nilai integrasinya adalah,
→
If
= Ih + chp ,
If
= I2h + c(2h)p ,
→
If
= I4h + c(4h)p ,
→
c=
If − Ih
hp
If − I2h
c=
(2h)p
If − I4h
c=
(4h)p
(6.47)
(6.48)
(6.49)
Hilangkan c pada persamaan (6.47) dan (6.48),
If − Ih
hp
If − Ih
If − I2h
=
=
If − I2h
(2h)p
hp
1
= p
p
p
2 h
2
(6.50)
seterusnya, hilangkan c pada persamaan (6.48) dan (6.49), diperoleh,
If − I2h
(2h)p
If − I2h
If − I4h
Eleminasi bentuk
=
=
If − I4h
(4h)p
2p hp
1
= p
4p hp
2
(6.51)
1
pada persamaan (6.50) dan (6.51),
2p
If − Ih
If − I2h
=
If
=
If − I2h
If − I4h
Ih I4h − (I2h )2
Ih − 2I2h + I4h
(Ih − I2h )2
= Ih −
Ih − 2I2h + I4h
(6.52)
Persamaan (6.52) disebut persamaan Ekstrapolasi Aitken.
6.5
Integrasi Numerik Gauss
Metode-metode integrasi numerik yang telah kita pelajari pada bab-bab se-
belumnya dihitung berdasarkan interpolasi linear, kuadratik dan kubik. Pada sub-bab
ini, kita akan pelajari metode integrasi numerik berdasarkan pada integrasi eksak polinomial berderajat tinggi dan tidak ada pembagian interval menjadi sub-interval.
Pendekatan integrasi yang berbeda dengan metode Newton-Cotes ini dikembangkan oleh Gauss dan dinamakan metode Kuadratur Gauss atau Gaussian Quadratur.
6.5 Integrasi Numerik Gauss
147
Metode ini tidak lagi menggunakan titik-titik yang berjarak sama, tetapi nilai integrasi
cukup diperoleh dengan menghitung nilai fungsinya pada titik tertentu.
Y
y = f (x)
X
−1
x1
O
x2
1
Gambar 6.8 Integral f (x) pada interval [−1, 1] yang didekati dengan
kuadratur Gauss
Perhatikan Gambar 6.8. Sebuah garis lurus di tarik dari kedua titik pada kurva
y = f (x), yaitu x1 dan x2 . Titik-titik tersebut di atur sedemikian rupa untuk menyeimbangkan galat positif dan galat negatif. Luas daerah yang dihitung sekarang adalah
luas daerah dibawah garis lurus,
1
If =
−1
f (x)dx = c1 f (x1 ) + c2 f (x2 )
(6.53)
dengan c1 , c2 , x1 dan x2 adalah nilai sembarang. Persamaan (??) disebut persamaan
kuadratur Gauss. Pada persamaan (6.8) mempunyai 4 buah variabel yang tidak
diketahui, untuk itu akan dibuat empat buah persamaan yang memuat c1 , c2 , x1 dan x2
dan dapat diselesaikan secara simultan.
Selanjutnya kita akan gunakan persamaan (6.53) untuk f (x) = 1, f (x) = x, f (x) =
x2 dan f (x) = x3 .
Untuk f (x) = 1, maka f (x1 ) = 1 dan f (x2 ) = 1 sehingga
1
−1
x
dx = c1 (1) + c2 (1)
1
−1
= c1 + c 2
2 = c1 + c2
(6.54)
148
Bab 6 Integrasi Numerik
Untuk f (x) = x, maka f (x1 ) = x1 dan f (x2 ) = x2 sehingga
1
−1
xdx = c1 (x1 ) + c2 (x2 )
1 2
x
2
1
= c1 (x1 ) + c2 (x2 )
−1
0 = c1 x1 + c2 x2
(6.55)
Untuk f (x) = x2 , maka f (x1 ) = x21 dan f (x2 ) = x22 sehingga
1
−1
x2 dx = c1 (x21 ) + c2 (x22 )
1 3
x
3
1
−1
2
3
= c1 (x21 ) + c2 (x22 )
= c1 x21 + c2 x22
(6.56)
Untuk f (x) = x3 , maka f (x1 ) = x31 dan f (x2 ) = x32 sehingga
1
−1
x3 dx = c1 (x31 ) + c2 (x32 )
1 4
x
4
1
−1
= c1 (x21 ) + c2 (x22 )
0 = c1 x31 + c2 x32
(6.57)
Dari hasil integral di atas, diperoleh empat persamaan nonlinear untuk empat variabel
tak diketahui, c1 , c2 , x1 , x2 . Dengan menggunakan eleminasi diperoleh,
c1 = c2 = 1
dan
1
x1 = √ ,
3
Jadi hasil yang dimaksud, adalah
1
1
x1 = − √
3
1
f (x)dx = f √
3
−1
−1
+f √
3
(6.58)
Persamaan
di atas disebut kaedah Gauss-Legendre 2 titik. Bentuk lain kuadratur gauss
1
selain
−1
f (x)dx adalah
∞
0
e−x f (x)dx,
∞
−∞
2
e−x f (x)dx
6.5 Integrasi Numerik Gauss
149
Untuk Gauss-Legendre 3 titik, dapat ditulis sebagai berikut
1
If =
−1
f (x)dx = c1 f (x1 ) + c2 f (x2 ) + c3 f (x3 )
(6.59)
dengan c1 , c2 , c3 , x1 , x2 dan x3 adalah variabel-variabel tak diketahui. Untuk itu akan
ditentukan variabel-variabel tersebut dengan membuat 6 persamaan yang melibatkan 6
variabel tak diketahui. Dengan mengasumsikan bahwa kuadratur Gauss bernilai tepat
untuk 6 fungsi, f (x) = 1, f (x) = x, f (x) = x2 , f (x) = x3 , f (x) = x4 dan f (x) = x5 .
Dengan menyelesaikan enam persamaan secara simultan, diperoleh,
c1 = 5/9,
dan
,
x1 = −
c2 = 8/9,
3
,
5
c3 = 5/9
,
x2 = 0,
x3 =
3
5
sehingga diperoleh rumusan Kuadratur Gauss-Legendre tiga titik,
, 1
5
f (x)dx = f −
9
−1
3
5
8
5
+ f (0) + f
9
9
, 3
5
(6.60)
Dari hasil yang diperoleh pada metode kuadratur Gauss dua titik dan tiga titik, dapat
dikembangkan untuk n titik yang diberikan oleh,
1
If =
−1
f (x)dx = c1 f (x1 ) + c2 f (x2 ) + c3 f (x3 ) + · · · + cn f (xn )
(6.61)
Hasil integrasi dari persamaan di atas menghasilkan 2n variabel tak diketahui, x1 , x2 , . . . , xn ,
c1 , c2 , . . . , cn , Dengan menerapkan terhadap terhadap f (x) = 1, x, . . . , x2n−1 terdapat
2n persamaan non linear,
2 = c1 + c 2 + · · · + cn
0 = c1 x1 + c2 x2 + · · · + cn xn
2
= c1 x21 + c2 x22 + · · · + cn x2n
3
0 = c1 x31 + c2 x32 + · · · + cn x3n
..
.
2
= c1 x2n−2
+ c2 x2n−2
+ · · · + cn x2n−2
n
1
2
2n − 1
0 = c1 x2n−1
+ c2 x2n−1
+ · · · + cn x2n−1
n
1
2
(6.62)
150
Bab 6 Integrasi Numerik
Tabel 6.3 Hasil pendekatan kuadratur Gauss-Legendre untuk n = 2, 3, 4, 5
dan n = 6
n
xi
ci
Galat Pemotongan
2
±0,5773502692
1,0000000000
≈ f (4) (ζ)
3
±0,7745966692
0,0000000000
0,5555555556
0,8888888889
≈ f (6) (ζ)
4
±0,8611363116
±0,3399810436
0,3478548451
0,6521451549
≈ f (8) (ζ)
5
±0,9061798459
±0,5384693101
0,0000000000
0,2369268851
0,4786286705
0,5688888889
≈ f (10) (ζ)
6
±0,9324695142
±0,6612093865
±0,2386191861
0,1713244924
0,3607615730
0,4679139346
≈ f (12) (ζ)
Tabel 6.3 menunjukkan hasil pendekatan kuadratur gauss-legendre untuk beberapa titik.
Penggunaan kaedah kudratur Gauss hanya dapat dilakukan pada interval [−1.1].
Persoalan akan muncul jika selang yang tersedia tidak demikian. Untuk itu, langkah
yang dapat diambil supaya persoalan dapat diselesaian adalah dengan mentranformasi
persoalan ke bentuk kuadratur Gauss.
Misalnya kita akan menghitung integral berikut ini.
b
f (x)dx
1
Untuk mentranformasi ke bentuk
a. selang [a, b] menjadi [−1.1]
−1
a
f (x)dx, maka harus dilakukan mengubah:
b. peubah x menjadi peubah t
c. diferensial dx menjadi dt
Dengan membandingkan kedua interval,
x−a
b−a
=
t − (−1)
1 − (−1)
6.5 Integrasi Numerik Gauss
151
t+1
x−a
=
b−a
2
2x − 2a = (t + 1)(b − a)
2x = a + b + bt − at
1
x =
((a + b) + (b − a)t)
2
(6.63)
dan
b−a
dt
(6.64)
2
Dari hasil transformasi variabel di atas dapat
ditulis kembali dengan menyulikan perdx =
b
samaan (6.63) dan (6.64) ke dalam bentuk
b
1
f (x)dx =
a
=
f (x)dx, yang ditulis
a
(a + b) + (b − a)t (b − a)
dt
f
2
2
−1
1
(a + b) + (b − a)t
(b − a)
f
dt
2
2
−1
Contoh 6.5
Hitunglah integral berikut.
2
1
(x2 + 1)dx
dengan menggunakan kaedah Gauss-Legendre 2 titik.
Penyelesaian:
Tentukan terlebih dahulu transformasi yang diperlukan.
1
((a + b) + (b − a)t)
2
1
((1 + 2) + (2 − 1)t)
=
2
= 1, 5 + 0, 5t
x =
dan dx = 0, 5dt, sehingga bentuk transformasinya adalah
2
1
(x2 + 1)dx =
1
−1
= 0, 5
(1, 5 + 0, 5t)2 + 1 0, 5dx
1
−1
2
(1, 5 + 0, 5t) + 1 dx
Dari bentuk di atas diperoleh bahwa
f (x) = (1, 5 + 0, 5t)2 + 1
(6.65)
152
Bab 6 Integrasi Numerik
maka
1
√
3
f
1
f −√
3
=
1
1, 5 + (0, 5) √
3
=
= 4, 1993587371
−1
1, 5 + (0, 5) √
3
= 2, 4673079295
sehingga hasil integralnya adalah,
2
1
(x2 + 1)dx = 0, 5
1
(1, 5 + 0, 5t)2 + 1 dx
−1
1
1
= 0, 5 f √
+ f −√
3
3
= 3, 33333333333
Jika nilai pendekatan kuadratur gauss-Legendre 2 titik di atas di bandingkan dengan
nilai sejatinya,
2
1
(x2 + 1)dx =
1 3
x
3
2
1
= 3, 3333333333
maka untuk 10 desimal, hasil pendekatan bernilai sama dengan nilai sejatinya.
Latihan
6.2
1. Hampiri integral-integral berikut dengan menggunakan kuadratur Gauss untuk
n = 2, dan bandingan hasilnya dengan nilai sebernarnya.
1,5
a.
c.
e.
g.
2
x ln xdx
10,35
0
π/4
0 3,5
3
1
b.
2
dx
2
x −4
d.
e3x sin 2xdx
f.
x
√
dx
2
x −4
h.
0
x2 ex dx
π/4
0
1,6
x2 sin xdx
2x
dx
x2 − 4
1 3π/4
0
2. Kerjakan lagi soal no. 1 untuk n = 3 dan n = 4
cos2 xdx
6.6 Integral Tak Wajar
6.6
153
Integral Tak Wajar
Pada umumnya perhitungan integral melibatkan interval terbatas,namun kadang
kala persoalan integral tak wajar muncul pada perhitungan numerik. Salah satu penyebab munculnya integral tak wajar adalah salah satu atau kedua-dua batas integral
adalah bilangan tak hingga, atau fungsi integranya tidak terdefinisi pada titik tertentu
yang ditunjukkan pada Gambar 6.9.
Y 6
a
b
X
-
Gambar 6.9 Kurva y = f (x) singular pada sisi kiri x = a.
Perhatian integral berikut,
b
a
dx
(x − a)p
akan konvergen jika dan hanya jika 0 < p < 1, dan pada kasus ini
b
a
(b − a)1−p
dx
=
(x − a)p
1−p
Misalkan f adalah suatu fungsi yang dapat ditulis dalam bentuk
f (x) =
g(x)
,
(x − a)p
dengan 0 < p < 1 dan g kontinu pada interval [a, b], maka integral tak wajar
b
f (x)dx
a
adalah ada. Selanjutnya kita akan menghampiri integral ini dengan menggunakan aturan Simpson gabungan. Jika g ∈ C 5 [a, b], kita akan membangun polinomial
154
Bab 6 Integrasi Numerik
orde 4, P4 (x) untuk fungsi g disekitar a,
P4 (x) = g(a) + g (a)(x − a) +
dan kita tulis
b
f (x) =
g (a)
g (a)
g (4) (a)
(x−)2 +
(x − a)3 +
(x − a)4
2!
3!
4!
b
g(x) − P4 (x)
(x − a)p
dan secara eksak kita dapat menghitung,
a
a
b
P4 (x)
a
dx +
b
P4 (x)
dx =
(x − a)p
=
sedangkan untuk
a
4 b (k)
g (a)
k=0 a
4
k!
kita definsikan,
G(x) =
(x − a)p
⎧
⎨ g(x) − P4 (x) ,
⎩
dx
(x − a)p
0,
(6.66)
(x − a)k−p dx
g (k) (a)
(b − a)k+1−p
k!(k
+
1
−
p)
k=0
b
g(x) − P4 (x)
a
(x − a)p
(6.67)
dx
jika a < x ≤ b,
jika x = a
(
Sehingga 0 < p < 1 dan P4 k)(a) sesuai dengan g (k) (a) untuk setiap k = 0, 1, 2, 3, 4 dan
G ∈ C 4 [a, b].
Contoh 6.6
Hampiri integral tak wajar berikut.
2 x
e
0
√ dx,
x
dengan menggunakan aturan Simpson gabungan dengan h = 0, 25 di sekitar a = 0
Penyelesaian:
Dari soal di atas kita peroleh, bahwa g(x) = ex . Untuk itu. kita akan hampiri g(x) = ex
dengan Polinomial Taylor orde 4, P4 (x) di sekitar x0 = 0,
g (a)
g (a)
g (4) (a)
(x−)2 +
(x − a)3 +
(x − a)4
2!
3!
4!
e0
e0
e0
= e0 + e0 (x − 0) + (x − 0)2 + (x − 0)3 + (x − 0)4
2!
3!
4!
x2 x3 x4
+
+
= 1+x+
2!
3!
4!
P4 (x) = g(a) + g (a)(x − a) +
6.6 Integral Tak Wajar
155
sehingga kita punya,
1
P4 (x)
0
√
1
1
=
x
0
1
x2 1x3 x4
√
+
+
1+x+
x
2!
3!
4!
1
1
1
x−/2 + x1/2 + x3/2 + x5/2 + x7/2
2
6
24
0
2
1
1
1 9/2
x
= lim 2x1/2 + x3/2 + x5/2 + x7/2 +
3
5
21
108
c→0+
1
1
2 1
+
= 2+ + +
3 5 21 108
≈ 2, 9235450
=
1
c
Dengan mengambil h = 0, 25, maka nilai-nilai hampiran dari
G(x) =
⎧
⎨ g(x) − P4 (x) ,
⎩
(x − a)p
0,
jika a < x ≤ b,
jika x = a
diberikan pada Tabel 6.4. Dengan menggunakan aturan Simpson Gabungan,
Tabel 6.4 Nilai hampiran G(x) dengan h = 0, 25
i
0
1
2
3
4
1
0
x
0,00
0,25
0,50
0,75
1,00
G(x)
0
0,0000170
0,0004013
0,0026026
0,0099485
h
[G(x0 ) + 4G(x0 ) + 2G(x2 ) + 4G(x3 ) + G(x4 )]
3
0, 25
[0 + 4(0, 0000170) + 2(0, 0004013) + 4(0, 0026026) + 0, 0099485
=
3
= 0, 0017691
G(x)dx ≈
Berdasarkan rumus
1 x
e
0
√ dx =
x
1
P4 (x)
0
√
x
1
dx +
0
G(x)dx
dan diperoleh hasil,
1 x
e
0
√ dx ≈ 2, 9235450 + 0, 0017691 = 2, 9253141
x
156
Bab 6 Integrasi Numerik
Y 6
Y6
y = f (x)
y = f (−z)
X
a
−b
b
(a) Kurva y = f (x) yang singular
pada sisi kanan x = b
−a
Z
-
(b) Kurva y = f (x) yang singular
pada sisi kiri z = −b
Gambar 6.10 Tranformasi bentuk fungsi y = f (x)
Persoalan di atas terjadi pada singular di titik batas kiri.Untuk menghampiri integral tak wajar yang singular pada titik sebelah kanan, kita akan menyederhanakan
teknik-teknik yang telah kita pelajari tetapi kita akan mengekspan bentuk pada titik b
menggantikan titik sebelah kiri a yang ditunjukkan pada Gambar Dengan melakukan
substitusi integral tak wajar dalam bentuk lain, yaitu
z = −x,
dz = −dx
untuk mengubah integral tak wajar ke dalam bentuk
b
−a
f (x)dx =
a
−b
(−z)dz
(6.68)
yang mempunyai kesingularan pada titik sebelah kiri. Integral tak wajar yang mempunyai singular di dalam interval, misalkan di titik c dengan a < c < b, maka integral
di ubah dalam bentuk jumlah integral, yaitu:
b
c
f (x)dx =
b
f (x)dx +
a
a
f (x)dx
c
Jenis integral tak wajar lainnya adalah bentuk integrasi yang melibatkan batas tak
hingga, yang secara dasar diberikan ole bentuk integral,
∞
f (x)dx,
a
yang akan di ubah dalam bentuk integral dengan singularits sebelah kiri dengan memisalkan
t = x−1 ,
dt = −x−2 dx,
oleh karena itu
dx = −x2 dx = −t−2 dt
6.6 Integral Tak Wajar
maka
157
∞
0
f (x)dx =
1/a
a
p
t (−t
−2
)dt = −
0
1
1/a
t2−p
dt
dengan menggunakan sifat-sifat integral,
∞
1/a
f (x)dx =
a
0
1
dt
t2−p
Dengan
cara yang sama, mengubah variabel t = x−1 terhadap integral tak wajar
∞
f (x)dx kedalam bentuk integral tak wajar dengan singularitas pada titik sebelah
a
kiri,
∞
1/a
f (x)dx =
0
a
1 −2
t dt =
t
f
1/a
0
1
dt
t
t−2 f
(6.69)
Contoh 6.7
Hampiri integral tak wajar berikut,
∞
I=
−3/2
x
1
1
sin
dx
x
dengan lebar h = 0, 125 Penyelesaian:
Dengan mengubah variabel kebentuk t = x−1 , maka kita peroleh
1
I=
0
t−1/2 sin tdt =
1
sin t
0
√ dx
t
sehingga
I=
1
sin t
√ dx =
t
0
1
P4 (t)
0
√
t
+
1
sin t − P4 (t)
√
0
t
Langkah pertama yang dilakukan adalah menggunakan hampiran polinomial
Taylor orde 4, P4 (t) terhadap sin t disekitar a = 0,
g (a)
g (a)
g (4) (a)
(t − a)2 +
(t − a)3 +
(t − a)4
2!
3!
4!
(− sin(0))
−(cos(0))
sin(0)
(t − 0)2 +
(t − 0)3 +
(t − 0)4
= sin(0) + cos(0)(t − 0) +
2!
3!
4!
1
t3
= t − t3
= t+
3!
6
P4 (t) = g(a) + g (a)(t − a) +
maka
1
P4 (t)
0
1
1
t1/2 − t5/2 dt
6
0
1
1
2 3/2
t − t7/2
=
3
21
0
= 0, 61904761
√ dt =
t
158
Bab 6 Integrasi Numerik
sedangkan
G(x) =
⎧
1
⎨ (sin t) − t + 6 t3
⎩
t1/2
0,
, jika 0 < t ≤ 1,
jika t = 0
Oleh karena h = 0, 125 maka jumlah sub-iterval adalah n = 8, sehingga dengan menggunakan aturan Simpson Gabungan diperoleh
1
0
G(t)dt =
1
(sin t) − t + 16 t3
≈
t1/2
0
h
[G(x0 ) + 4G(x1 ) + 2G(x2 ) + 4G(x3 ) + 2G(x4 )
3
+4G(x5 ) + 2G(x6 ) + 4G(x7 ) + G(x8 )
= 0, 0014890097
Untuk itu, hasil integral tak wajar adalah
I=
1
sin t
0
1 sin t − P (t)
1 P (t)
4
√ dx =
√ 4
√
+
t
t
t
0
0
= 0, 0014890097 + 0, 61904761 = 0, 62953661
dengan akurasi 4, 0 × 10−8
6.6 Integral Tak Wajar
159
Latihan
6.3
1. Gunakan aturan Simpson Gabungan dan n yang diberikan untuk menghampiri
integral tak wajar berikut,
1
a.
0
2
c.
1
−1/4
x
sin xdx,
n=4
b.
ln x
dx,
(x − 1)1/5
n=8
d.
1 2x
e
0
√
5
x2
dx,
1
cos 2x
x1/3
0
n=6
dx,
n=6
2. Gunakan aturan Simpson Gabungan dan n yang diberikan untuk menghampiri
integral tak wajar berikut,
1
a.
0
0
c.
1/2
e−x
√
dx,
1−x
−1
√
3
n=6
1
dx,
3x + 1
b.
0
2
n=6
d.
0
1
dx,
(2x − 1)/3
3
xex
dx,
(x − 1)2
n=4
n=8
3. Dengan menggunakan tranformasi t = x−1 , gunakan aturan Simpson Gabungan
dan n yang diberikan untuk menghampiri integral-integral tak wajar berikut.
∞
a.
c.
1
1
dx,
x2 + 9
∞
cos x
1
x3
dx,
∞
n=4
n=6
b.
d.
1
1
dx,
1 + x4
∞ −4
x
1
sin x
dx,
n=4
n=8
4. Tentukan polinomial Lagrange {L0 , L1 , L2 , L3 } yang diberikan oleh,
L0 (x) = 1,
L1 (x) = 1 − x,
L2 (x) = x2 − 4x + 2,
L3 (x) = −x3 + 9x2 − 18x + 6
menjadi ortoghonal pada interval (0, ∞) berkaitan dengan fungsi
e−x . Polinomial
∞
polinomial tersebut dapat digunakan untuk menghampiri
menyebabkan integral tak wajar ini ada.
0
e−x f (x)dx, yang
160
Bab 6 Integrasi Numerik
5. Misalkan sebuah benda massa m bergerak vertikal ke atas dengan titik awal pada
permukaan bumi x = R. Jika gaya gesekan udara di abaikan, dan kecepatan
benda v diberikan oleh,
2
v = 2gR
∞
0
z −2 dz,
dengan z =
x
R
dan g adalah gaya gravitasi bumi dengan nilai g = 9, 8m/s2 dan R = 3960 mil,
hampiri kecepatan benda v tersebut.
BAB 7
PENYELESAIAN PERSAMAAN DIFERENSIAL
BIASA SECARA NUMERIK
7.1 Persamaan Diferensial Orde Satu
7.1.1 Persamaan Dengan Variabel Terpisah
Pandang kembali persamaan difenrensial linear orde satu berikut,
f (x)
dy
=
dx
g(y)
Ubah persamaan di atas ubah dalam bentuk terpisah,
g(y)dy = f (x)dx
Persamaan di atas disebut persamaan terpisah. Dengan mengintegralkan setiap ruasnya, diperoleh,
g(y)dy =
f (x)dx + C
G(y) = F (x) + C
dengan G(y) dan F (x) masing-masing anti turunan dari g(y) dan f (x).
Contoh 7.1
Selesaikan persamaan diferensial berikut.
9yy + 4x = 0.
Penyelesaian:
(7.1)
162
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
Dengan memisahkan variabel akan diperoleh bentuk persamaan
9ydy = −4dx
Integralkan kedua ruas, diperoleh penyelesaian umum,
9 2
y = −2x2 + c,
2
x2 y 2
+
= C
9
4
(7.2)
dengan C = c/18 Persamaan di atas adalah keluarga dari persamaan ellips. Gambar
?? menunjukkan kurva persamaan ellips untuk beberapa nilai C.
2
y
1
–4
0
–2
2
4
x
–1
–2
Gambar 7.1 Kurva persamaan
x2
9
+
y2
4
= C dengan C = 1 dan C = 2.
Contoh 7.2 Masalah nilai awal
Selesaikan masalah nilai awal berikut.
y + 5x4 y 2 dx = 0,
y(0) = 1
Penyelesaian:
Dengan menggunakan variabel terpisah, diperoleh persamaan,
dy
= −54 dx
y2
7.1 Persamaan Diferensial Orde Satu
163
Integralkan kedua ruas,
dy
y2
1
−
y
= −
54 dx
= −x5 + c,
y =
x5
1
−c
Oleh karena syarat awal diberikan y(0) = 1, maka
y(0) =
1
= 1
0−c
1
= 1
−c
c = −1
sehingga penyelesaian khusus untuk masalah nilai awal tersebut adalah
y=
7.1.2
1
x5 + 1
Persamaan Homogen
Secara umum, persamaan diferensial (PD) orde satu ditulis,
a0 (x) +
dy
+ a1 (x)y = g(x)
dx
(7.3)
dengan a0 (x), a1 (x) dan g(x) adalah fungsi-fungsi x yang terdefenisi pada interval I.
Jika di andaikan bahwa a0 = 0, maka pembagian dengan a0 menghasilkan
y + p(x)y = f (x)
(7.4)
dengan p(x) = a1 (x)/a0 (x) dan f (x) = g(x)/a0 (x).
Agar persamaan (7.4) lebih sederhana dan mudah diselesaikan, maka dilakukan
penggantian p(x) dengan a, sehingga persamaan (7.4) menjadi
y + ay = f (x)
(7.5)
adalah tidak eksak. Selanjutnya, kalikan dengan eax (faktor integrasi) terhadap kedua
ruas persamaan (7.5),
164
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
eax (y + ay) = f (x)eax
adalah eksak. Pada kalkulus dasar, diperoleh bahwa
d
ax
dx (e y)
(7.6)
dy
= aeax y + eax dx
, maka
persamaan (7.5) ditulis kembali menjadi
d ax
(e y) = f (x)eax
dx
(7.7)
Dengan mengintegralkan persamaan di atas diperoleh
ax
e y=
f (x)eax dx + c
dengan c adalah konstanta tetap. Penyelesaian y dari persamaan di atas diberikan oleh,
y = e−ax
f (x)eax dx + ce−ax
(7.8)
Selanjutnya, persamaan (7.4) dapat juga di selesaikan dengan faktor integral fungsi µ(x)
yang memenuhi,
d
µ(x)y
dx
µ(x)y + µ(x)p(x)y = µ (x)y + µ(x)y µ(x)[y + p(x)y] =
Jika diasumsikan bahwa, y(x) = 0, maka
µ (x) = µ(x)p(x)
µ (x)
= p(x)
µ(x)
dµ(x) 1
= p(x)
dx µ(x)
Dengan menggunakan metode integral terpisah, diperoleh penyelesaian µ(x) >
0,
1
dµ(x) =
µ(x)
p(x)dx
p(x)dx
lnµ(x) =
-
µ(x) = e
p(x)dx
(7.9)
7.2 Metode Euler
165
-
Seterusnya faktor integrasi µ(x) = e
p(x)dx
dikalikan terhadap kedua ruas pada per-
samaan (7.4) dan diperoleh,
-
e
p(x)dx
-
(y + p(x)y) = f (x)e
p(x)dx
(7.10)
Pada kalkulus dasar diperoleh bahwa
d e
dx
p(x)dx
-
y(x) = e
p(x)dx y (x) + y(x)p(x)
maka
d e
dx
p(x)dx
-
p(x)dx
d e
-
e
-
y(x)
= e
-
y(x)
p(x)dx
p(x)dx
=
e
y(x) =
y(x) = e−
-
e
-
f (x)
p(x)dx
p(x)dx
p(x)dx
f (x) dx
f (x)dx + c
-
f (x)e
p(x)dx
+ ce−
-
p(x)dx
7.2 Metode Euler
7.2.1 Tafsiran Metode Euler
Diberikan persamaan diferensial orde satu,
dy
= f (x, y),
dx
dan y(x0 ) = y0
dan mempunyai penyelesaian φ(x). Misalkan h > 0 adalah tetap, maka dapat dibentuk
selang baru yang lebarnya sama,
xn = x0 + nh,
n = 0, 1, 2, . . .
Selanjutnya kita akan membentuk nilai yn yang mendekati penyelesaian φ(x) sebagai
berikut. Pada titi (x) , y0 ), maka kemiringan dari
dy
dx
= f (x, y) diberikan oleh dy/dx =
f (x0 , y0 ). Sehingga persamaan garis terhadap kurva pada titik awal (x0 , y0 ) diberikan
oleh,
y = y0 + (x − x0 )f (x0 , y0 )
(7.11)
166
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
Dengan menggunakan garis tangen untuk menghampiri φ(x), kita akan menemukan
titik x1 = x0 + h,
φ(x1 ) ≈ y1 = y0 + hf (x0 , y0 )
(7.12)
Selanjutnya, untuk titik x1, y1 , kita akan membentuk garis yang arah kemiringannya
diberikan oleh medan arah pada titik x1, y1 , yang artinya sama dengan f (x1 , y1 dan
akan muncul hampiran,
φ(x2 ) ≈ y2 = y1 + hf (x1 , y1 )
(7.13)
Jika proses inti terus dilakukan secara berulang, maka
φ(x3 ) ≈ y3 = y2 + hf (x2 , y2 )
φ(x4 ) ≈ y4 = y3 + hf (x3 , y3 )
..
.
φ(xi+1 ) ≈ yi+1 = yi + hf (xi , yi )
dengan i = 1, 2, 3, . . . , n
7.2.2
Analisis Galat Metode Euler
Meskipun metode Eluer sederhana, tetapi ia mengandung dua macam galat, yaitu galat
pemotongan (truncation error dan galat longgokan (cumulative error. Galat pemotongan dapat langsung ditentukan oleh,
1
Ep ≈ h2 y”(t) = O(h2 )
2
(7.14)
Galat pemotongan ini sebanding dengan kuadrat terkecil ukuran langkah h sehingga disebut juga galat perlangkah atau galat lokal. Semakin kecil nilai h yang berarti semakin banyak langkah perhitungannya, semakin kecil pula galat perhitungannya. Galat soulsi pada langkah ke-k adalah tumpukan galat dari galat-galat sebelumnya.
Galat yang terkumpul pada akhir langkah ke-k ini disebut galat longgokan. Jika langkah
dimulai dari x) = A sampai terakhir di xn = b, maka galat totalnya terkumpul di yn ,
yaitu,
Etotal =
n
1 2
h y”(t)
k=1
2
7.2 Metode Euler
167
h2
y”(t)
2
(b − a) 2
h y”(t)
2h
(b − a)
y”(t)h
2
= n
=
=
Contoh 7.3
Diketahui persamaan diferensial biasa,
dy
=x+y
dx
dan
y(0) = 1
Gunakan metode Euler untuk menghitung y(0, 10) dengan ukuran langkah h = 0, 05
dan h = 0, 02. Jumlah angka penting adalah 5. Diketahui penyelesaian persamaan
diferensial tersebut y(x) = ex − x − 1
Penyelesaian:
(a) Untuk h = 0, 05
Diketahui a = x0 = 0, b = 0, 10, h = 0, 05
Dalam hal ini, f (x, y) = x + y dan penerapan metode Euler pada persamaan diferensial
tersebut menjadi,
yi+1 = y1 + 0, 05(xi + yi )
Langkah-langkah yang dilakukan:
x0 = 0 → y0 = 1
x1 = 0, 05 → y1 = y0 + 0, 05(x0 + y0 ) = 1 + (0, 05)(0 + 1) = 1, 0050
x2 = 0, 10 → y2 = y1 + 0, 05(x1 + y1 ) = 1, 0050 + (0, 05)(0, 05 + 1, 0050)
= 1, 05775
Jika nilai sejati dari y(0, 10) = e0,10 − 0, 01 − 1 = 1, 1103, maka galatnya adalah
E(x) = 1, 1103 − 1, 05775 (b) Untuk h = 0, 02
Diketahui a = x0 = 0, b = 0, 10, h = 0, 02
Dalam hal ini, f (x, y) = x + y dan penerapan metode Euler pada persamaan diferensial
tersebut menjadi,
yi+1 = y1 + 0, 02(xi + yi )
Langkah-langkah yang dilakukan:
168
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
x0 = 0 → y0 = 1
x1 = 0, 02 → y1 = y0 + 0, 02(x0 + y0 ) = 1 + (0, 02)(0 + 1) = 1, 0200
x2 = 0, 04 → y2 = y1 + 0, 02(x1 + y1 ) = 1, 0200 + (0, 02)(0, 02 + 1, 0200) = 1, 0408
x3 = 0, 06 → y3 = 1, 0624
x4 = 0, 08 → y4 = 1, 0848
x5 = 0, 10 → y5 = 1, 1081
Jika nilai sejati dari
y(0, 10) = e0,10 − 0, 01 − 1 = 1, 1103, maka galatnya adalah
E(x) = 1, 1103 − 1, 1081 = 0, 0021
Contoh 7.4
Pertimbangkan masalah nilai awal berikut.
y = 2xy,
, y(1) = 1
Gunakan metode Euler untuk menghampiri y(1, 5) dengan h = 0, 1 dan h = 0, 05.
Penyelesaian:
Langkah pertama adalah mengidentifikasi bahwa f (x, y) = 2xy, oleh karena itu,
yn+1 = yn + h(2xn yn )
Untuk h = 0, 1,
Dari soal diperoleh x0 = 1, y0 = 1, maka dapat kita peroleh langkah ke-1,
y1 = y0 + h(2x0 y0 )
= 1 + (0, 1)[2(1)(1)]
= 1, 2
Nilai-nilai dari hasil iterasi ditunjukkan pada Tabel 7.1.
Selanjutnya, untuk h = 0, 05,maka x0 = 1 dan y0 = 1,
y1 = y0 + h(2x1 y1 )
= 1 + (0, 05)[2(1)(1)]
= 1, 1
7.2 Metode Euler
169
Tabel 7.1 Metode Euler dengan h = 0, 1
xn
yn
Nilai
sejati
1,00
1,10
1,20
1,30
1,40
1,50
1,0000
1,2000
1,4640
1,8154
2,2874
2,9278
1,0000
1,2337
1,5527
1,9937
2,6117
3,4904
Galat
% Galat
relatif
0,0000
0,0337
0,0887
0,1784
0,3244
0,5625
0,00
2,73
5,71
8,95
12,42
16,12
dan
y2 = y1 + h(2x1 y1 )
= 1, 1 + (0, 05)[2(1, 05)(1, 1)]
= 1, 12155
Nilai-nilai dari hasil iterasi ditunjukkan pada Tabel 7.2.
Tabel 7.2 Metode Euler dengan h = 0, 05
xn
yn
Nilai
sejati
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,0000
1,1000
1,2155
1,3492
1,5044
1,6849
1,8955
2,1419
2,4311
2,7714
3,1733
1,0000
1,1079
1,2337
1,3806
1,5527
1,7551
1,9937
2,2762
2,6117
3,0117
3,4904
Galat
% Galat
relatif
0,0000
0,0079
0,0182
0,0314
0,0483
0,0702
0,0982
0,1343
0,1806
0,2403
0,3171
0,00
0,072
1,47
2,27
3,11
4,00
4,93
5,90
6,92
7,98
9,08
Pada contoh di atas nila sejati adalah dihitung dari solusi yang diketahui y =
2
ex −1 .
Begitu juga dengan galat relatif persentase, dihitung berdasarkan
170
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
|nilai sejati − hampiran|
× 100
nilai sejati
Contoh 7.5
Gunakan metode Eluer untuk menghampiri nilai y(0, 5) dari penyelesaian
y = (x + y − 1)2 ,
y(0) = 2
Penyelesaian:
Untuk n = 0 dan h = 0, 1, kita punya
y1 = y0 + (0, 1)(x0 + y0 − 1)2
= 2 + (0, 1)(0 + 2 − 1)2 = 2, 1
Hasil perhitungan selanjutnya dapat dilihat pada Tabel 7.3 untuk h = 0, 1 dan Tabel
7.4 untuk h = 0, 05
Tabel 7.3 Metode Euler dengan h = 0, 1
xn
0,00
0,10
0,20
0,30
0,40
0,50
yn
2,0000
2,1000
2,2440
2,4525
2,7596
3,2261
Latihan
7.1
1. Gunakan metode Euler untuk menghampiri penyelesaian persamaan diferensial
berserta nilai awal berikut dengan h = 0, 1 dan h = 0, 05.
7.2 Metode Euler
171
Tabel 7.4 Metode Euler dengan h = 0, 05
xn
yn
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
a. y = 2x − 3y + 1,
b.
y
= 4x − 2y,
y(0) = 2;
c. y = 1 + y 2 ,
f. y = x + y 2 ,
y
g. y = xy − ,
x
h. y = y − y 2 ,
y(0, 5)
y(0) = 1;
y(0) = 0;
y(0, 5)
y(0, 5)
y(0) = 0;
2
y(1, 5)
y(0, 5)
y(0) = 0;
d. y = x2 + y 2 ,
e. y = e−y ,
y(1) = 5;
2,0000
2,0500
2,1105
2,1838
2,2727
2,3812
2,5142
2,6788
2,8845
3,1455
3,4823
y(0, 5)
y(1) = 1;
y(0, 5)
y(0) = 0, 5;
y(0, 5)
2. Gunakan metode Euler untuk menghampiri penyelesaian persamaan diferensial
berserta nilai awal berikut.
a. y = te3t − 2y,
0 ≤ y ≤ 1,
b. y = 1 + (t − y)2 ,
c.
y
= 1 + y/t,
y(0) = 0, h = 0, 5
2 ≤ t ≤ 3, ,
1 ≤ t ≤ 2,
y(2) = 1, h = 0, 5
y(1) = 2, h = 0, 25
d. y = cos 2t + sin 3t, 0 ≤ t ≤ 1,
, y(0) = 1, h = 0, 25
e. y = 2x − 3y
3. Berikut diberikan penyelesaian dari persamaan-persamaan diferensial pada soal
no. 1. Bandingan galat dari setiap soal!
a. y(t) = 15 te3t −
1 3t
25 e
+
1 −2t
25 e
b. y(t) = t +
1
1−t
172
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
c. y(t) = t ln t + 2t
1
2
d. y(t) =
sin 2t − 13 cos 3t +
4
3
4. Gunakan metode Euler untuk menghampiri penyelesaian setiap persamaan diferensial dan masalah
nilai awal berikut.
y
y 2
a. y = −
, 1 ≤ t ≤ 2, y(1) = 1, h = 0, 1
t
t y y 2
, 1 ≤ t ≤ 3, y(1) = 0, h = 0, 2
b. y = 1 +
t t
c. y = −(y + 1)(y + 3), 0 ≤ t ≤ 2, y(0) = −2, h = 0, 2
d. y = −5y + 5t2 + 2t,
y(0) = 13 , h = 0, 1
0 ≤ t ≤ 1,
5. Diberikan masalah nilai awal,
2
y = y + t2 et ,
t
1 ≤ t ≤ 2,
y(1) = 0
dengan penyelesaian sejati
y(t) = t2 (et − e)
a. Gunakan metode Euler dengan h = 0, 1 untuk mendekati penyelesaian tersebut dan bandingkan dengan nilai sebenarnya
b. Gunakan jawaban yang diperoleh dari (a) dan interpolasi linear untuk menghampiri nilai-nilai y berikut dan bandingkan dengan nilai sebernarnya.
(i) y(1, 04)
(ii) y(1, 55)
(iii) y(1, 97)
6. Diberikan masalah nilai awal,
y =
1
y
− − y2,
t2
t
1 ≤ t ≤ 2,
y(1) = −1
dengan penyelesaian sejati
y(t) = −
1
t
a. Gunakan metode Euler dengan h = 0, 05 untuk mendekati penyelesaian tersebut dan bandingkan dengan nilai y sebenarnya
b. Gunakan jawaban yang diperoleh dari (a) dan interpolasi linear untuk menghampiri nilai-nilai y berikut dan bandingkan dengan nilai sebernarnya.
(i) y(1, 052)
(ii) y(1, 555)
(iii) y(1, 978)
7.3 Metode Heun(Perbaikan Metode Euler)
173
7. Pada sebuah rangkaian yang menunjukkan tegangan V , resistensi R, induksi L,
dan kapasitas C pada rangkaian paralel, arus i memenuhi persamaan diferensial
berikut,
di
d2 V
1
1 dV
=C 2 +
+ V
dt
dt
R dt
L
Misalkan C = 0, 3 faraday, R = 1, 4 ohm, L = 1, 7 henri dan tegangan diberikan
oleh,
V (t) = e−0,06πt sin(2t − π)
Jika i(0) = 0, tentukan arus i untuk t = 0, 1j dengan j = 0, 1, 2, . . . , 100
7.3
Metode Heun (Perbaikan Metode Euler)
Metode Euler mempunyai ketelitian yang rendah, karena galatnya besar seband-
ing dengan h), sehingga perlunya perbaikan dengan mengurangi galatnya, dan hal ini
dilakukan dengan menggunakan metode Heun (mofified Euler’s method. Pada metode
Heun, penyelesaian awal dijadikan sebagai nilai perkiraan awal (prediktor) dan selanjutnya penyelesaian perkiraan awal diperbaiki dengan metode Heun (corrector). Pandang
suatu persamaan diferensial orde satu sebagai berikut.
dy
= y = f (x, y)
dx
Jika diintegrasikan kedua ruas persamaan dari dalam interval [xk , xk+1 ],
xk+1
f (x, y)dx =
xk
xk+1
y (x)dx
xk
= y(xk+1 ) − yxk
= yk+1 − yk
Nyatakan yk+1 diruas kiri dan suku-suku yang lainnya di ruas kana,
yk+1 = yk +
xk+1
f (x, y)dx
(7.15)
xk
Suku pada ruas kanan, dapat diselesaikan dengan menggunakan kaidah trapesium,
xk+1
xk
dx ≈
h
[f (xk , yk ) + f (xk+1 , yk+1 )]
2
(7.16)
Substitusikan persamaan (7.16) ke dalam persamaan (7.15) dan diperoleh,
yk+1 ≈ yk +
h
∗
[f (xk , yk ) + f (xk+1 , yk+1
)]
2
(7.17)
174
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
dengan
∗
yk+1
= yk + hf (xk , yk )
Bentuk persamaan di atas adalah metode Heun (Metode Euler-Cauchy yang
diperbaiki). Pada persamaan (7.17), suku ruas kanan mengandung yk+1 , dan ini merupakan penyelesaian awal (prediktor) yang dihitung dengan metodr Euler. Karena itu,
persamaan (7.17) dpat ditulis,
prediktor : y ( 0)r+1 = yr + hf (xr , yr )
(0)
corrector : yr+1 = yr + h/2[f (xr , yr ) + f (xr+1 , yr+1 )]
atau ditulis dalam bentuk umum,
yk+1 = yk +
h
[f (xk , yk ) + f (xk+1 , yk ) + hf (xk , yk )]
2
(7.18)
(0)
Analisis Galat Suku h/2[f (xr , yr )+f (xr+1 , yr+1 )] bersesuain dengan kaidah trapesium
pada integrasi numerik, sehingga galat untuk metode Heun sama dengan galat metode
trapesium, yaitu
h3
y”(t),
12
= O(h3 )
Ep ≈ −
xk < t < xk+1
(7.19)
sedangkan galat longgokannya adalah
EL =
n
k=1
−
1 3
h y”(t)
12
(b − a) 2
h y”(t)
12
= O(h2 )
= −
(7.20)
Galat longgokan metode Heun sebnding dengan h2 . Hal ini berarti penyelesaian persamaan diferensial biasa dari metode Heun lebih baik dari metode Euler, tetapi jumlah
komputasinya lebih banyak.
Contoh 7.6
Hitunglah hampiran metode Euler yang diberbaiki terhadap penyelesaian φ(x) = ex
dari
y = y,
y(0) = 1
7.3 Metode Heun(Perbaikan Metode Euler)
175
pada x = 1 dan lebar langkah h = 1, 10−1 , 10−2 , 10−3 , 10−4 Penyelesaian:
Kita mulai dengan x0 = 0 dan y0 = 1. Karena f (x, y) = y, maka persamaan (7.17)
menjadi
h
h2
[yn + (yn + hyn )] = yn + hyn + yn
2
2
yn+1 = yn +
yaitu,
yn+1 =
h2
1+h+
2
Oleh karena y0 = 1, maka diperoleh,
yn =
h2
1+h+
2
yn ,
(7.21)
n
,
n = 0, 1, 2, . . .
Untuk memperoleh pendekatan pada x = 1, kita harus mempunyai 1 = x0 + nh = nh
dan oleh karena itu n = 1/h. Disini hampiran Euler yang diperbaiki adalah e = φ(1)
yaitu
h2
1+h+
2
1/h
Contoh 7.7
Pertimbangkan masalah nilai awal berikut.
y = 2xy,
y(1) = 1
dengan menggunakan metode Euler diperbaiki untuk menghampiri pada y(1, 5) untuk
h = 0, 1 dan h = 0, 05
Penyelesaian:
Untuk h = 0, 1, dimulai dengan x0 = 1 maka
y1∗ = y0 + hf (x0 , y0 ) = 1 + (0, 1)[2(1)(1)] = 1, 2
dan
h
(f (x0 , y0 ) + f (x1 , y1∗ ))
2
0, 1
([2(1)(1)] + [2(1, 1)(1, 2)])
= 1+
2
= 1, 232
y1 = y0 +
176
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
Tabel 7.5 Metode Heun dengan h = 0, 1 untuk solusi y = 2xy
xn
yn
Nilai
sejati
1,00
1,10
1,20
1,30
1,40
1,50
1,0000
1,2320
1,5479
1,9832
2,5908
3,4509
1,0000
1,2337
1,5527
1,9937
2,6117
3,4904
Galat
% Galat
relatif
0,0000
0,0017
0,0048
0,0106
0,0209
0,0394
0,00
0,14
0,31
0,53
0,80
1,13
Nilai-nilai selanjutnya dapat dilihat pada Tabel 7.5. sedangkan untuk h = 0, 05 dengan
x0 = 1 maka
y1∗ = y0 + hf (x0 , y0 ) = 1 + (0, 05)[2(1)(1)] = 1, 1
dan
h
(f (x0 , y0 ) + f (x1 , y1∗ ))
2
0, 05
([2(1)(1)] + [2(1, 1)(1, 1)])
= 1+
2
= 1, 1077
y1 = y0 +
nilai-nilai selanjutnya dapat dilihat pada Tabel 7.6.
Contoh 7.8
Pertimbangkan masalah nilai awal berikut.
y = (x + y − 1)2 ,
y(0) = 2
dengan menggunakan metode Euler diperbaiki untuk menghampiri pada y(0, 5) untuk
h = 0, 1 dan h = 0, 05
Penyelesaian:
Untuk h = 0, 1, maka
y1∗ = y0 + h(x0 + y0 − 1)2 = 2 + (0, 1)(0 + 2 − 1)2 = 2, 1
7.3 Metode Heun(Perbaikan Metode Euler)
177
Tabel 7.6 Metode Heun dengan h = 0, 05 untuk solusi y = 2xy
xn
yn
Nilai
sejati
1,00
1,05
1,10
1,15
1,20
1,25
1,30
1,35
1,40
1,45
1,50
1,0000
1,1077
1,2332
1,3798
1,5514
1,7531
1,9909
2,2721
2,6060
3,0038
3,4795
1,0000
1,1079
1,2337
1,3806
1,5527
1,7551
1,9937
2,2762
2,6117
3,0117
3,4904
Galat
% Galat
relatif
0,0000
0,0002
0,0004
0,0008
0,0013
0,0020
0,0029
0,0041
0,0057
0,0079
0,0108
0,00
0,02
0,04
0,06
0,08
0,11
0,14
0,18
0,22
0,26
0,31
dan
h
(f (x0 , y0 ) + f (x1 , y1∗ ))
2
h
= y0 + [(x0 + y0 − 1)2 + (x1 + y1∗ − 1)2 ]
2
0, 1
[1 + 1, 44]
= 2+
2
= 2, 122
y1 = y0 +
untuk nilai-nilai selanjutnya dapat dilihat pada Tabel 7.7.
Tabel 7.7 Metode Heun dengan h = 0, 1 untuk solusi y = (x + y − 1)2
xn
yn
0,00
0,10
0,20
0,30
0,40
0,50
2,0000
2,1220
2,3049
2,5858
2,0378
3,8254
178
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
Sedangkan untuk h = 0, 05,
y1∗ = y0 + h(x0 + y0 − 1)2 = 2 + (0, 05)(0 + 2 − 1)2 = 2, 05
dan
h
(f (x0 , y0 ) + f (x1 , y1∗ ))
2
h
= y0 + [(x0 + y0 − 1)2 + (x1 + y1∗ − 1)2 ]
2
= 2, 0553
y1 = y0 +
untuk nilai-nilai selanjutnya dapat dilihat pada Tabel 7.8
Tabel 7.8 Metode Heun dengan h = 0, 05 untuk solusi y = (x + y − 1)2
7.4
xn
yn
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
2,0000
2,0553
2,1228
2,2056
2,3075
2,4342
2,5931
2,7953
3,0574
3,4057
3,8840
Metode Taylor Orde Tinggi
Metode Euler pada dasarnya diturunkan berdasarkan deret Taylor orde satu,
sehingga galat yang dihasilkan adalah O(h). Untuk meperbaiki penyelesaian persamaan
diferensial yang melibatkan suatu metode tertentu, maka diusahakan bagaimana agar
galat menjadi sekecil mungkin dengan melihat galat pemotongan lokal, yaitu O(hp ).
Untuk akan dibuat sedemikian rupa agar p sebesar mungkin.
Oleh karena metode Euler diturunkan dari deret Taylor orde satu, maka dari itu
dapat dikembangkan suatu metode yang memenuhi sifat-sifat konvergensi dari metode
selisih untuk nilai n yang lebih besar.
7.4 Metode Taylor Orde Tinggi
179
Misalkan penyelesaian y(t) dengan masalah nilai awal,
y = f (t, y),
a ≤ t ≤ b,
y(a) = α
mempunyai derivatif sebanyak (n + 1). Jika kita mengekspan penyelesaian tersebut,
y(t), di dalam suku-suku ke-n dari deret Taylor disekitar ti , akan kita peroleh,
y(ti+1 ) = y(ti ) + hy (ti ) +
+
h2 hn (n)
y (ti ) + · · · +
y (ti )
2
n!
hn+1 (n+1)
y
(ζi )
(n + 1)!
(7.22)
untuk ζi dalam (ti , ti+1 ).
Suksesif diferensiasi penyelesaian y(t) memberikan,
y (t) = f (t, y(t))
y (t) = f (t, y(t))
..
.
y (k) (t) = f (k−1) (t, y(t))
Substitusikan hasil di atas ke persamaan (7.22) dan memberikan,
y(ti+1 ) = y(ti ) + hf (ti , y(ti )) +
+
h2 hn (n−1)
f (ti , y(ti )) + · · · +
f
(ti , y(ti ))
2
n!
hn+1 (n)
f (ζi , y(ζi ))
(n + 1)!
(7.23)
Metode persamaan selisih yang berkorespondensi dengan persamaan (7.23) diperoleh
dengan menghilang suku terakhir yang memuat bentuk ζ. Metode ini disebut Metode
Taylor orde n: dan diperoleh,
w0 = α
w1 = w0 + hT (n) (t0 , w0 )
..
.
wi+1 = wi + hT (n) (ti , wi ),
untuk i = 0, 1, 2, . . . , N − 1
dengan
T (n) (ti , wi ) = f (ti , wi ) +
h hn−1 (n−1)
f (ti , wi ) + · · · +
f
(ti , wi )
2
n!
(7.24)
180
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
Contoh 7.9
Dengan menggunakan metode Taylor orde dua dan empat terhadap masalah nilai awal,
y = y − t2 + 1,
0 ≤ t ≤ 2,
y(0) = 0, 5
Penyelesaian:
Bentuk
y = y − t2 + 1
diubah menjadi
f (t, y(t)) = y(t) − t2 + 1,
maka tiga turunan pertamanya adalah,
d
(y − t2 + 1)
dt
= y − 2t
f (t, y(t)) =
= y − t2 + 1 − 2t
d
(y − t2 + 1 − 2t)
dt
= y − 2t − 2 = y − t2 + −2t − 2
f (t, y(t)) =
= y − t2 − 2t − 1
dan
d
(y − t2 − 2t − 1)
dt
= y − 2t − 2 =
f (t, y(t)) =
= y − t2 − 2t − 1
Oleh karena itu, untuk orde dua,
h f (ti , wi )
2
h
= (wi − t2i + 1) + (wi − t2i − 2ti + 1)
2
h
h
= (wi − t2i + 1) + (wi − t2i + 1) + (2ti )
2
2
h
2
1+
(wi − ti + 1) − hti
=
2
T (ti , wi ) = f (ti , wi ) +
7.4 Metode Taylor Orde Tinggi
181
dan w0 = 0, 5, sehingga berdasarkan rumus deret Taylor orde 2, diperoleh
wi+1 = wi + h
1+
h
(wi − t2i + 1) − hti
2
sedangkan untuk orde 4,
h h2
h3
f (ti , wi ) + f (ti , wi ) + f (ti , wi )
2
6
24
h
h2
= (wi − t2i + 1) + (wi − t2i − 2ti + 1) + (wi − t2i − 2ti − 1)
2
6
3
h
+ (wi − t2i − 2ti − 1)
24
h
h2
h3
= (wi − t2i ) + (wi − t2i ) + (wi − t2i ) + (wi − t2i )
2
6
24
2
3
h2
h3
h
h
h
h
+ (−2ti ) + (−2ti ) + (−2ti ) + 1 + (1) + (−1) + (−1)
2
6
24
2
6
24
T (4) (ti , wi ) = f (ti , wi ) +
=
h h2 h3
+
1+ +
2
6
24
+1 +
(wi −
t2i )
h h2
− 1+ +
3 12
(hti )
h h2 h3
−
−
2
6
24
dan w0 = 0, 5 sehingga berdasarkan rumus deret Taylor orde 4, diperoleh
wi+1 = wi + h
h h2 h3
+
1+ +
2
6
24
h h2 h3
+1 + −
−
2
6
24
(wi −
t2i )
h h2
− 1+ +
3 12
hti
untuk i = 0, 1, 2, . . . , N − 1 Jika kita ambil lebar h = 0, 2, maka jumlah iterasi N = 10
dan ti = 0, 2i untuk i = 1, 2, . . . , 10.
Dengan memasukan nilai-nilai pada rumus, maka hasil yang diperoleh untuk
orde 2, adalah
w0 = 0, 5
0, 2
(wi − 0, 04i2 + 1) − 0, 04i
2
= 1, 22wi − 0, 0088i2 − 0, 008i + 0, 22
wi+1 = wi + 0, 2
1+
dan untuk orde ke 4, adalah
wi+1 = wi + 0, 2
0, 2 0, 04 0, 008
+
+
1+
(wi − 0, 04i2 )
2
6
24
182
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
0, 2 0, 04
0, 2 0, 04 0, 008
(0, 04i) + 1 +
+
−
−
− 1+
3
12
2
6
24
= 1, 2214wi − 0, 008856i2 − 0, 00856i + 0, 2186
dengan i = 0, 1, 2, . . . , 9.
Latihan
7.2
1. Gunakan metode Taylor orde dua untuk menghampiri penyelesaian dari setiap
masalah nilai
2 awal berikut.
y
y
+
,
1 ≤ t ≤ 1, 2, y(1) = 1, h = 0, 1
a. y =
t
t
b. y = sin(t) + e−t ,
0 ≤ t ≤ 1,
y(0) = 0, h = 0, 5
1
c. y = (y 2 + y),
1 ≤ t ≤ 3,
y(1) = −2, h = 0, 5
t
4t
0 ≤ t ≤ 1,
y(0) = 1, h = 0, 25
d. y = −ty + ,
y
2. Ulangi no. 1 untuk metode Taylor orde 4
3. Gunakan metode Taylor orde dua dengan h = 0, 1 untuk menghampiri penyelesaian dari
y = 1 + t sin(ty),
0 ≤ t ≤ 2,
y(0) = 0
1 ≤ t ≤ 2,
y(1) = 0
1 ≤ t ≤ 2,
y(1) = −1
4. Diberikan masalah nilai awal,
2
y = y + t2 et ,
t
5. Diberikan masalah nilai awal berikut.
y =
1
y
− − y2,
2
t
t
dengan penyelesaian sejati y(t) = −1/t
a. Gunakan metode Taylor orde dua dengan h = 0, 05 untuk menghampiri
penyelesaian dan bandingkan dengan nilai y
7.5 Metode Runge-Kutta
183
b. Gunakan jawaban pada bagian (a) dan interpolasi linear untuk menghampiri
nilai-nilai y berikut
(i) y(1, 052)
(ii) y(1, 555)
(iii) y(1, 978)
c. Gunakan metode Taylor orde dua dengan h = 0, 05 untuk menghampiri
penyelesaian dan bandingan dengan nilai y sebenarnya.
d. Gunakan jawaban pada (c) dan interpolasi sebagian-sebagian Hermit untuk
menghampiri nilai y dan bandingkan dengan nilai-nilai:
(i) y(1, 052)
7.5
(ii) y(1, 555)
(iii) y(1, 978)
Metode Runge-Kutta
Penyelesaian persamaan diferensial biasa dengan menggunakan metode Taylor
tidka praktis, karena metode tersbut membutuhkan perhitungan turunan f (x, y), dan
juga tidak semua fungsi mudah dihitung turunannya, terutama fungsi-fungsi yang rumit.
Metode Runge-Kutta merupakan alternatif lain dari metode Taylor yang tidak
membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian
yang tinggi dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi
dengan jalan mengevaluasi fungsi f (x, y) pada titik terpilih setiap selang.
Bentuk umum metode Runge-Kutta orde n ditulis sebagai berikut,
yk+1 = yk + a1 y1 + a2 k2 + · · · + an yn
(7.25)
dengan a1 , a2 , · · · , an adalah konstanta dan
k1 = hf (xr , yr )
k2 = hf (xr + p1 h, yr + q11 k1 )
k3 = hf (xr + p2 h, yr + q21 k1 + q22 k2 )
..
.
kn = hf (xr + pn−1 h, yr + qn1,1 k1 + qn−1,2 k2 + · · · + qn−1,n1 kn−1 )
Nilai ai , pi , qij dipilih sedemikian rupa sehingga dapat meminumkan galat. Galat langkah
metode Runge-Kutta orde-n adalah O(hn+1 )
Galat longgokan metode Runge-Kutta orde ke-n adalah O(hn )
184
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
a. Metode Runge-Kutta Orde Satu
Metode Runge-Kutta orde satu ditulis,
k1 = hf (xr .yr )
yr+1 = yr + (a1 k1 )
(7.26)
Galat perlangkah adalah O(h2 )
Galat longgokan adalah O(h)
Yang termasuk ke dalam metode Runge-Kutta orde satu adalah metode Euler.
b. Metode Runge-Kutta Orde Dua
Metode Runge-Kutta orde dua ditulis,
k1 = hf (xr , yr )
k2 = hf (xr + p1 h, yr + q11 k1 )
yr+1 = yr + (a1 k1 + a2 k2 )
(7.27)
Galat perlangkah adalah O(h3 )
Galat longgokan adalah O(h2 )
c. Metode Runge-Kutta Orde Tiga
Metode Runge-Kutta orde tiga terkenal dan banyak dipakai dalam praktek. Metode
tersebut mempunyai ketelitian penyelesaiannya tingggi dibandingkan dengan dua metode
sebelumnya.
Metode Runge-Kutta orde tiga ditulis,
k1 = hf (xr , yr )
1
1
k2 = hf (xr + h, yr + k1 )
2
2
k3 = hf (xr + h, yr − k1 + 2k2 )
1
yr+1 = yr + (k1 + 4k2 + k3 )
6
(7.28)
7.5 Metode Runge-Kutta
185
Galat perlangkah adalah O(h4 )
Galat longgokan adalah O(h3 )
d. Metode Runge-Kutta Orde Empat
Metode Runge-Kutta orde empat mempunyai ketelitian lebih baik dibandingakan dengan metode Runge-Kutta orde tiga. Metode Runge-Kutta orde tiga ditulis,
k1 = hf (xr , yr )
1
1
k2 = hf (xr + h, yr + k1 )
2
2
1
1
k3 = hf (xr + h, yr + k2 )
2
2
k4 = hf (xr + h, yr + k3 )
1
yr+1 = yr + (k1 + 4k2 + k3 )
6
(7.29)
Galat perlangkah adalah O(h4 )
Galat longgokan adalah O(h3 )
Contoh 7.10
Gunakan metode Runge-Kutta dengan h = 0, 1 untuk menghampiri y(1, 5) terhadap
penyelesain
y = 2xy,
y(1) = 1
Penyelesaian:
Kita mulai dengan mengambil x0 = 1 dan n = 0, maka
k1 = hf (x0 , y0 )
= (0, 1)(2x0 y0 )
k2
= (0, 1)[2(1)(1)] = 0, 2
1
1
= hf x0 + h, y0 + k1
2
2
1
1
= (0, 1)2 x0 + h
y0 + k1
2
2
1
1
= (0, 1)2 1 + (0, 1)
1 + (0, 2)
2
2
= 0, 231
186
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
1
1
k3 = hf x0 + h, y0 + k2
2
2
1
1
= (0, 1)2 x0 + h
y0 + k2
2
2
1
1
= (0, 1)2 1 + (0, 1)
1 + (0, 231)
2
2
= 0, 234255
k4 = hf (x0 + h, y0 + k3 )
= (0, 1)2(x0 + h)(y0 + k3)
= (0, 1)(1 + 0, 1)(1 + 0, 234255) = 0, 2715361
dan oleh karena itu,
1
yn+1 = y0 + (k1 + 2k2 + 2k3 + k4 )
6
1
= 1 + (0, 2 + 2(0, 231) + 2(0, 234155) + 0, 2715361)
6
= 1, 23367435
Jika kita ambil empat desimal dibelakang koma, maka
y1 = 1, 2337
Dengan cara yang sama diperoleh nilai-nilai y2 , y3 , y4 , y5 berikut sebagaiman yang ditunjukkan pada Tabel 7.9, sedangkan perbandingan nilai-nilai dari beberapa metode
yang telah digunakan terhadap penyelesaian y = 2xy dengan nilai awal y(1) = 1 dan
h = 0, 1 ditunjukkan pada Tabel 7.10.
Tabel 7.9 Metode Runge-Kutta dengan h = 0, 1 untuk solusi y = 2xy
xn
yn
Nilai
sejati
Galat
% Galat
relatif
1,00
1,10
1,20
1,30
1,40
1,50
1,0000
1,2337
1,5527
1,9937
2,6116
3,4902
1,0000
1,2337
1,5527
1,9937
2,6117
3,4904
0,0000
0,0000
0,0000
0,0000
0,0001
0,0001
0,00
0,00
0,00
0,00
0,00
0,00
7.5 Metode Runge-Kutta
187
Tabel 7.10 Perbandingan metode Euler, Heun dan Runge-Kutta untuk solusi
y = 2xy dengan h = 0, 1
Perbandingan metode Numerik dengan h = 0, 1
Runge
Nilai
xn
Euler
Heun
Kutta
sejati
1,00
1,10
1,20
1,30
1,40
1,50
1,0000
1,2000
1,4640
1,8154
2,2874
2,9278
1,0000
1,2320
1,5479
1,9832
2,5908
3,4509
0,0000
1,2337
1,5527
1,9937
2,6116
3,4902
1,0000
1,2337
1,5527
1,9937
2,6117
3,4904
Latihan
7.3
1. Gunakan metode Runge-Kutta untuk menyelesaikan masalah nilai awal berikut
dengan h = 0, 1 untuk memperoleh hampiran empat desimal.
a. y = 2x − 3y + 1,
b. y = 4x − 2y,
c.
y
=1+
y(0) = 2;
y2 ,
y(0) = 0;
d. y = x2 + y 2 ,
e. y = e−y ,
f.
y
=x+
y(1) = 5;
y(0) = 0;
h.
=y−
y2 ,
y(0, 5)
y(0, 5)
y(0, 5)
y(0) = 0;
g. y = xy 2 − y/x,
y
y(0, 5)
y(0) = 1;
y2 ,
y(1, 5)
y(0, 5)
y(1) = 1;
y(0) = 0, 5;
y(0, 5)
y(0, 5)
2. Gunakan metode Runge-Kutta dengan h = 0, 1, h = 0, 05 dan h = 0, 01 untuk
mengestimasi penyelesaian masalah nilai awal berikut di x = 1. Bandingkan
hasil-hasil tersebut dengan nilai sejati.
a. y 2x + 2y, y(0) = 1
c.
y
=
ey ,
y(0) = 0
b. y = 1/y,
d.
y
y(0) = 1
= y − sin x,
y(0) = −1
188
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
3. Gunakan metode Runge-Kutta dengan h = 0, 2 untuk menentukan hampiran terhadap penyelesaian masalah nilai awal berikut.
t2 y − 3ty + 3y = 1,
y(1) = 0,
y (1) = 0
Hitunglah penyelesaian sejati dan selanjutnya bandingkan hasilnya!
4. Jika gaya gesekan udara berbanding kuadrat dengan kecepatan, dan kecepatan v
dari sebuah massa m yang jatuh dari ketinggian h di tentukan oleh,
m
dv
= mg − kv 2 ,
dt
k>0
Jika v(0) = 0, k = 0, 125, m = 5 slugs, dan g = 9, 8 m/s2 , gunakan metode RungeKutta untuk menentukan nilai hampiran kecepatan massa jatuh setela 5 detik.
(Gunakan h = 1).
5. Misalkan y(x) adalah solusi dari masalah nilai awal berikut.
y = x2 + y 3 ,
y(1) = 1
Hitunglah rumusan Runge-Kutta yang digunakan untuk memperoleh hampiran
untuk y(1, 4. (gunakan h = 0, 1).
7.6
Metode Banyak Langkah
Pada pembahasan terdahulu mengenai metode penyelesaian persamaan diferen-
sial orde satu biasanya disebut metode satu langkah, karena hampiran yang dilakukan
untuk titik mesh t + i + 1 melibatkan informasi dari hanya satu titik sebelumnya, yaitu
titik mesh ti . Semua informasi yang digunakan pada metode-metode tersebut diperoleh
di luas interval yang mana penyelesaian akan di hampiri.
Oleh karena itu hampiran dari penyelesaian diperoleh pada setiap titik mesh
t0 , t1 , t2 , . . . ti sebelum hampiran ti+1 diperoleh, dan hal ini menyebabkan galat |yj (hampiran)−
y(tj )| cenderung meningkat. Untuk itu, cukup beralasan jika dikembangkan hampiran
yang menggunakan banyak titik mesh yang lebih akurat untuk menghampiri penyelesaian pada ti+1 .
Metode yang menggunakan banyak titik sebelumnya untuk menghitung hampiran titik berikutnya disebut metode banyak langkah.
7.6 Metode Banyak Langkah
189
Definisi 7.1
Metode banyak langkah untuk menyelesaikan masalah nilai awal,
y = f (x, y),
a ≤ x ≤ b,
y(a) = α,
(7.30)
adalah suatu persamaan selisih untuk menentukan hampiran yi+1 pada titik mesh
xi+1 dapat direprensetasikan oleh persamaan berikut, di mana m adalah bilangan
bulat lebih dari 1,
yi+1
= am−1 yi + am−2 yi−1 + · · · + a0 wi+1−m
+h[bm f (xi+1 , yi+1 ) + bm−1 f (xi , yi )
+ · · · + b0 f (xi+ , yi+1−m )]
(7.31)
untuk i = m − 1, m, 0, 1, . . . , n − 1 dengan mengambil
y(x0 ) = y0 ,
y(x1 ) = y1 ,
y(x2 ) = y2 ,
...,
y(xm−1 ) = ym−1
dan h = (b − a)/n
Ketika bm = 0, metode disebut eksplisit atau terbuka, sehingga persamaan (7.31) memberikan yi+1 secara eksplisit pada suku-suku sebelumnya di hitung, sedangkan ketika
bm = 0, metode ini disebut implisit atau tertutup, sehingga yi+1 terjadi pada kedua sisi
persamaan (7.31)
7.6.1
Metode Adam-Bashford
a. Metode Adam-Bashford Dua Langkah
h
[3f (xi , yi )] − f (xi−1 , yi−1 )],
2
y(x0 ) = y0 , y(x1 ) = y1
yi+k = yi +
(7.32)
dengan i = 1, 2, 3, . . . , n
b. Metode Adam-Bashford Tiga Langkah
h
23f (xi , yi ) − 16f (xi−1 , yi−1 ) + 5f (xi−2 , yi−2 ) ,
12
y(x0 ) = y0 , y(x1 ) = y1 , y(x2 ) = y2
yi+k = yi +
dengan i = 2, 3, 4, . . . , n
(7.33)
190
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
c. Metode Adam-Bashford Empat Langkah
h
55f (xi , yi ) − 59f (xi−1 , yi−1 ) + 37f (xi−2 , yi−2 )
24
−9f (xi−3 , yi−3 )
yi+k = yi +
y(x0 ) = y0 ,
y(x1 ) = y1 ,
y(x2 ) = y2 ,
(7.34)
y(x3 ) = y3
dengan i = 3, 4, . . . , n
d. Metode Adam-Bashford Lima Langkah
h
1901f (xi , yi ) − 2774f (xi−1 , yi−1 ) + 2616f (xi−2 , yi−2 )
720
−1274f (xi−3 , yi−3 ) + 251f (xi−4 , yi−4 )
(7.35)
yi+k = yi +
y(x0 ) = y0 ,
y(x1 ) = y1 ,
y(x2 ) = y2 ,
y(x3 ) = y3 ,
y(x4 ) = y4
dengan i = 4, 5, 6 . . . , n
7.6.2
Metode Adam-Moulton
a. Metode Adam-Moulton Dua Langkah
h
[5f (xi+1 , yi+1 )] + 8f (xi , yi ) − f (xi−1 , yi−1 )],
12
y(x0 ) = y0 , y(x1 ) = y1
yi+k = yi +
(7.36)
dengan i = 1, 2, 3 . . . , n − 1
b. Metode Adam-Moulton Tiga Langkah
h
9f (xi+1 , yi+1 )] + 19f (xi , yi ) − 5f (xi−1 , yi−1 )
24
+f (xi−2 , yi−2 )
yi+k = yi +
y(x0 ) = y0 ,
dengan i = 2, 3 . . . , n − 1
y(x1 ) = y1 ,
y(x2 ) = y2
(7.37)
7.6 Metode Banyak Langkah
191
c. Metode Adam-Moulton Empat Langkah
h
251f (xi+1 , yi+1 )] + 646f (xi , yi ) − 264f (xi−1 , yi−1 )
720
+106f (xi−2 , yi−2 ) − 19f (xi−3 , yi−3 )
yi+k = yi +
y(x0 ) = y0 ,
y(x1 ) = y1 ,
y(x2 ) = y2 ,
(7.38)
y(x3 ) = y3
dengan i = 3, 4, 5 . . . , n − 1
Contoh 7.11
Pertimbangkan masalah nilai awal berikut.
y = y − t2 + 1,
0 ≤ t ≤ 2,
y(0) = 0, 5
dan dekati dengan metode Adam-Bashford empat langkah dan metode Adam-Moulton
tiga langkah, gunakan h = 0, 2 untuk kedua metode.
Penyelesaian:
Dari rumusan metode Adam-Bashford empat langkah,
h
55f (xi , yi ) − 59f (xi−1 , yi−1 ) + 37f (xi−2 , yi−2 )
24
−9f (xi−3 , yi−3 )
yi+k = yi +
untuk i = 3, 4, . . . , 9. Dengan menyederhanakan dan gunakan f (t, y) = y − t2 + 1,
h = 0, 2, dan ti = 0, 2i, maka persamaan selisih metode Adam-Bashford empat langkah
menjadi,
yi+1 =
1
35yi − 11, 8yi−1 + 7, 4yi−2 − 1, 8yi−3 − 0, 192i2 − 0, 192i + 4, 736
24
Hasil-hasil hampiran untuk metode di atas ditunjukkan pada Tabel ??.
Sedangkan persamaan selisih metode Adam-Moulton tiga langkah adalah,
h
9f (xi+1 , yi+1 )] + 19f (xi , yi ) − 5f (xi−1 , yi−1 )
24
+f (xi−2 , yi−2 )
yi+k = yi +
192
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
untuk i = 2, 3, 4, . . . , 9 dan dengan mereduksi fungsi f (t, y) = y − t2 + 1, h = 0, 2, dan
ti = 0, 2i, maka persamaan selisih metode Adam-Moulton tiga langkah menjadi,
yi+1 =
1
1, 8yi+1 + 27, 8yi − yi−1 + 0, 2yi−2 − 0, 192i2 − 0, 192i + 4, 736
24
Oleh karena kita gunakan metode eksplisit, maka penyelesaian untuk wi+1 adalah
yi+1 =
1
7, 8yi − yi−1 + 0, 2yi−2 − 0, 192i2 − 0, 192i + 4, 736
22, 2
Hasil-hasil hampiran dari metode Adam-Moulton tiga langkah ditunjukkan pada Tabel
7.11.
Tabel 7.11 Perbandingan metode Adam-Bashfor 4 langkah dan AdamMoulton 3 langkah untuk solusi y = y − t2 + 1 dengan h = 0, 2
Galat
xi
AdamBashford
yi
AdamMoulton
yi
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
0,5000000
0,8292986
1,2140877
1,6489406
2,1273124
2,6410810
3,1803480
3,7330601
4,2844931
4,8166575
5,3075838
0,0000000
0,0000000
0,0000000
0,0000000
0,0000828
0,0002219
0,0004065
0,0006601
0,0010093
0,0014812
0,0021119
0,0000
1,2337
1,5527
1,9937
2,6116
3,4902
0,0000
1,2337
1,5527
1,9937
2,6116
Galat
0,0000000
0,0000000
0,0000000
0,0000065
0,0000160
0,0000293
0,0000478
0,0000731
0,0001071
0,0001527
0,0002132
7.6 Metode Banyak Langkah
193
Latihan
7.4
1. Gunakan metode Adam-Bashford empat langkah untuk menhapiri penyelesaian
masalah nilai awal berikut. Pada setiap soal bandingkan hasil hampiran dengan
hasil sebenarnya.
a. y = te3t − 2y,
y(t) =
1 3t
5 te
−
0 ≤ t ≤ 1, y(0) = 0, h = 0, 2
1 3t
25 e
2
b. y = 1 + (t − y) ,
c. y = 1 + y/t,
d.
y
+
2 ≤ t ≤ 3,
1 ≤ t ≤ 2,
1
2
y(2) = 1, h = 0, 2;
y(1) = 2, h = 0, 2;
0 ≤ t ≤ 1,
= cos 2t + sin 3t,
y(t) =
1 −2t
25 e
sin 2t − 13 cos 3t +
1
1−t
y(t) = t ln t + 2t
y(t) = t +
y(0) = 1, h = 0, 2
4
3
2. Gunakan metode Adam-Bashford untuk menghampiri penyelesaian masalah nilai
awal berikut. Pada setiap soal gunakan nilai-nilai awal yang diperoleh dari metode
Runge-Kutta orde 3mpat. Bandingkan hasil tersebut denagn hasil sebenarnya.
a. y =
y
−
t
y
t
2
1 ≤ t ≤ 2, y(1) = 1, h = 0, 1,
,
y
y
b. y = 1 + +
t
t
y(t) = t tan(ln t)
2
,
c. y = −(y + 1)(y + 3),
1 ≤ t ≤ 3,
0 ≤ t ≤ 2,
y(t) =
t
1 + ln t
y(1) = 0, h = 0, 2;
y(0) = −2, h = 0, 1;
y(t) = −3 1+e2−2t
d. y = −5y + 5t2 + 2t,
0 ≤ t ≤ 1,
y(0) = 13 , h = 0, 1,
y(t) = t2 + 13 e−5t
3. Gunakan hasil dari soal no. 2 dan interpolasi linear untuk menghampiri nilai y(t)
dan bandingkan dengan nilai sebernarnya,
a. y(1,25) dan y(1,93)
b. y(2,1) dan y(2,75)
c. y(1,3) dan y(1,93)
d. y(0,54) dan y(0,94)
4. Ulangi soal-soal pada no. 2 dengan menggunakan metode Heun
194
Bab 7 Penyelesaian Persamaan Diferensial Biasa Secara Numerik
5. Ulangi soal-soal pada no.2 dengan menggunakan metode Titik tengah
6. Ulangi soal-soal pada no. 1 dengan menggunakan metode Runge-Kutta orde empat
7. Ulangi soal-soal pada no.2 dengan menggunakan metode Runge-Kutta orde empat
8. Metode Runge-Kutta orde empat dapat ditulis dalam bentuk,
w0 = α,
wi+1 = wi +
h
h
f (ti , wi ) + f (ti + α1 h, wi + δ1 f (ti , wi ))
6
3
h
+ f (ti + α2 h, wi + δ2 hf (ti + γh, wi + γ3 hf (ti , wi )))
3
h
+ f (ti + α3 h, wi + δ3 hf (ti + γ4 h, wi + γ5 hf (ti + γ6 h, wi + γ7 + hf (ti , wi ))))
6
Tentukan nilai-nilai dari konstanta,
α1 , α2 , α3 , δ1 , δ2 , δ3 , γ2 , γ3 , γ4 , γ5 , γ6 , γ7 .
DAFTAR PUSTAKA
Atkinson, K. E., Elementary Numerical Analysis. ,John Willey & Sons, Inc.,1995.
Chapra, Steven C., Numerical Methods for Engineers: with Programming and Software
Applications, McGraw-Hill, Singapore, 1998.
Hamming, Richard W., Introduction to Applied Numerical Analysis, McGraw-Hill,
New York, 1971.
Munif, A. & Prastyoko, A., Penguasaan dan Penggunaan Metode Numerik.,Institut
Teknologi Sepuluh Nopember Press, Surabaya, 1995.
Munir, R., Metode Numerik., Penerbit Informatika, Bandung, 2003.
Mathews, John H., Numerical Methods for Mathematics, Science and Engineering, 2
nd.,Prentice Hall International, Inc.,1992.
Kreyszig, E., Advanced Engineering Matehamatics, 8 th Ed., John Wiley & Sons., New
York., 1999.
Susila, I.N., Dasar-Dasar Metode Numerik, DIKNAS, Jakarta., 1993.
195