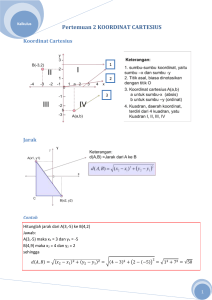
KATA PENGANTAR Puji syukur alhamdulillah kami ucapkan ke hadirat Tuhan Yang Maha Esa, karena telah melimpahkan rahmat-Nya berupa kesempatan dan pengetahuan sehingga makalah ini bisa selesai pada waktunya. Terima kasih juga kami ucapkan kepada teman-teman yang telah berkontribusi dengan memberikan ide-idenya sehingga makalah ini bisa disusun dengan baik dan rapi. Kami berharap semoga makalah ini bisa menambah pengetahuan para pembaca. Namun terlepas dari itu, kami memahami bahwa makalah ini masih jauh dari kata sempurna, sehingga kami sangat mengharapkan kritik serta saran yang bersifat membangun demi terciptanya makalah selanjutnya yang lebih baik lagi. Pekanbaru, 04 Oktober 2019 Penulis DAFTAR ISI DAFTAR TABEL DAFTAR GAMBAR BAB 1 PENDAHULUAN 1.1 Latar Belakang Masalah 1.1.1 Fungsi Penerapan fungsi dalam bidang ekonomi dan bisnis merupakan salah satu bagian yang sangat penting untuk dipelajari bagi para mahasiswa yang belajar di bidang ilmu ekonomi dan bisnis. Dalam banyak hal fungsi diterapkan dalam berbagai bidang untuk menyelesaikan persoalanpersoalan baik dalam bidang tehnik, ekonomi, dan bidang lain yang mempelajari hubungan-hubungan antar variabel, dimana variabel satu sama lainnyasaling pengaruh mempengaruhi dan dapat diukur, seperti jarak dan waktu dapat diiukur,sehingga dapat dikatakan bahwa jarak adalah fungsi dari waktu. 1.1.2 Fungsi Linier Hubungan sebab akibat antara beragai variabel ekonomi, misalnya antara permintaan dan harga, antara investasi dan tingkat bunga, dapat dengan mudah dinyatakan serta diterangkan dalam bentuk fungsi. Di antara berbagai macam hubungan fungsional yang ada, hubungan linear merupaka entuk yang paling dasar dan paling sering digunakan dalam analisis ekonomi. Bab ini menguraikan segala hal yang berkenaan dengan fungsi linear atau persamaan linear, serta model –model hubungan ekonomi yang mendsarkan diri padabentuk hubungan linear. Fungsi linier adalah fungsi yang paling sederhana karena hanya mempunyai satu variabel bebas dan berpangkat satu pada variabel bebas tersebut, sehingga sering disebut sebagai fungsi berderajad satu. Bentuk umum persamaan linier adalah: y = a + bx; dimana a adalah konstanta dan b adalah koefisien (b?0). Atau sering dinyatakan dalam bentuk implicit berikut: Ax + By + C = 0. Disamping itu jugs, fungdi ini merupakan dasar untuk mempelajari fungsi – fungsi lainnya yang lebih rumit dalam penyelesaiannya. 1.1.3 Sistem Persamaan Linier Kebanyakan model ekonomi yang berbentuk matematis mempunyai lebih dari satu kendala dan variabel dalam himpunan persamaannya. Jika setiap kendala dinyatakan sebagai suatu persamaan linier maka himpunan persamaan-persamaan linier ini disebut sebagai system persamaan linier. Dengan kata lain, suatu system linier adalah suatu himpunan yang terdiri atas dua atau lebih persamaan linier Banyaknya persamaan dan variabel dalam suatu system persamaan linier dapat dilihat pada dimensinya. Jika persamaan linier terdiri atas m persamaan dan n variabel, maka dapat dinyatakan bahwa system persamaan linier ini adalah system m x n 1.2 Rumusan Masalah 1. Apa itu fungsi dan hubungan ? 2. Apa itu variabel bebas dan terikat ? 3. Apa itu system Koordinat Cartesius ? 4. Apa itu fungsi dengan satu variabel bebas ? 5. Apa itu fungsi dengan dua variabel atau lebih variabel bebas ? 6. Apa itu kemiringan dan titik potong sumbu ? 7. Apa itu bentuk umum Fungsi Linier ? 8. Bagaimana cara menentukan Persamaan Garis ? 9. Apa itu hubungan dua garis lurus ? 10. Metode apa saja yang digunakan untuk memperoleh nilai-nilai penyelesaian dari system persamaan linier ? 11. Apa itu persamaan linier dan Ketidakkonsistenan ? 1.3 Tujuan Penulisan - Memahami apa itu Fungsi dan Hubungan - Memahami apa itu Variabel Bebas dan Terikat - Memahami Sistem Koordinat Cartesius - Mengetahui bentuk umum Fungsi Linier - Memahami cara menentukan Persamaan Garis - Memahami apa itu Hubungan Dua Garis Lurus - Mengetahui Metode-metode sistem persamaan linier - Memahami apa itu Persamaan linier dan Ketidakkonsistenan BAB 2 TINJAUAN PUSTAKA Fungsi Fungsi dalam matematika adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (codomain). Himpunan nilai yang diperoleh dari relasi tersebut disebut daerah hasil (range).Jika ada dua himpunan, yaitu himpunan A dan himpunan B, maka suatu fungsi dari himpunan A ke himpunan B adalah suatu relasi yang khusus, yaitu relasi dimana setiap anggota A dikawankan dengan tepat satu anggota B. Untuk mendefinisikan fungsi dapat digunakan notasi berikut. f:A→B Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik Fungsi Linier Fungsi linier adalah fungsi paling sederhana karena hanya mempunyai satu variabel bebas dan berpangkat satu dari variabel tersebut. Fungsi ini sering digunakan dalam penerapan ekonomi dan bisnis untuk menjelaskan hubunganhubungan ekonomi dan bisnis secara linier, Di samping itu fungsi ini merupakan dasar untuk mempelajari fungsi-fungsi lainnya yang lebih rumit dalam penyelesaiannya. Dalam matematika, istilah fungsi linear dapat mengacu kepada salah satu dari dua konsep berbeda namun berhubungan: • Fungsi polinomial orde satu, satu variabel; • Peta antara dua ruang vektor yang mempertahankan penjumlahan vektor dan perkalian Sistem Persamaan Linier Persamaan linear adalah persamaan aljabar di mana setiap periode adalah baik konstanatau produk dari konstan dan (kekuatan pertama) variabel tunggal.Persamaan linear dapat memiliki satu atau lebih variabel. Persamaan linear terjadiberlimpah di sebagian besar subareas matematika dan terutama dalam matematikaterapan. Sementara mereka muncul secara alami ketika model banyak fenomena, merekasangat berguna karena banyak persamaan non-linear dapat dikurangi menjadi persamaanlinear dengan mengasumsikan bahwa jumlah dari beragam kepentingan hanya sebagiankecil dari beberapa "latar belakang" kondisi. Persamaan linear tidak termasuk eksponen Dalam suatu sistem linier, terdapat tiga penyelesaia yang mungkin, yaitu : 1. Suatu sistem persamaan linier mempunyai suatu penyelesaian yang tunggal (unik) adalah suatu sistem persamaan yang konsisten (consistent). 2. Suatu sistem persamaan linier tidak mempunyai suatu penyelesaian adalah suatu sistem persamaan yang tidak konsisten (inconsistent). 3. Suatu sistem persamaan linier mempunyai sejumlah penyelesaian yang tidak terbatas adalah suatu persamaan yang saling ketergantungan (dependent) di antara satu dengan yang lainnya. BAB 3 PEMBAHASAN A. FUNGSI DAN HUBUNGAN Dalam mempelajari fungsi dan hubungan tentu terlebih dahulu kita harus memahami atau mengerti tentang konsep himpunan-khususnya pasangan urut (ordered option). Hal ini dikarenakan himpunan pasangan urut selalu menghubungkan dua elemen. Kedua elemen ini masing-masing dapat berbentuk bilangan nyata atau suatu variabel tertentu. Suatu fungsi dapat juga disebut “pemetaan” atau “transformasi”. Kedua istilah ini menyatakan suatu tindakan yang menghubungkan satu dengan yang lainnya. Dalam pernyataan Y=f(x), penulisan f dapat diartikan sebagai suatu aturan di mana himpunan X dipetakan atau ditransformasikan ke dalam himpunan Y. Hal ini dapat kita tulis menjadi, f: X→Y Fungsi adalah suatu hubungan di mana setiap elemen dari wilayah (domain) saling berhubungan dengan satu dan hanya satu elemen dari jangkauan (range). Dengan demikian,dari definisi fungsi ini dapat disimpulkan bahwa suatu fungsi adalah suatu hubungan (relasi), tetapi suatu hubungan belum tentu fungsi. 1 1 Matematika Ekonomi, Bisnis, Josep Bintang Kalangi, Edisi 4, Salemba 4, hlm 40 B. VARIABEL BEBAS DAN TERIKAT Pada pernyataan fungsi Y=f(x), variabel yang mewakili nilai-nilai domain disebut sebagai variabel bebas (independent variable) dan variabel yang mewakili nilai-nilai range disebut sebagai variabel terikat (dependent variable). Nilai-nilai variabel bebas ini dapat ditentukan secara bebas oleh analis dalam suatu masalah, sedangkan nilai-nilai dari variabel terikat hanya tergantung dari variabel bebas tadi Variabel bebas dapat dianggap sebagai variabel terikat atau sebaliknya variabel terikat dapat dianggap sebagai variabel bebas dalam suatu model tertentu. Sebagai contoh, diantara variabel harga (P) dengan variabel jumlah yang diminta (Q), sehingga variabel harga (P) dianggap sebagai variabel bebas dan dapat ditulis menjadi Q=f(P). Namun, sering kali variabel jumlah yang diminta (Q) yang mempengaruhi variabel harga (P), sehingga variabel jumlah yang diminta (Q) yang dianggap sebagai variabel bebas dan ditulis P =f(Q). Jadi, kedua variabel ini dapat saling dipertukarkan satu sama lainnya. Variabel-variabel ekonomi yang saling ketergantungan satu sama lainnya di dalam model ekonomi sering kita sebut dengan istilah model simultan. C. SISTEM KOORDINAT CARTESIUS Istilah kata Cartesius yang digunakan untuk mengenang seorang ahli matematika sekaligus seorang filsuf dari Perancis yaitu Rene Descartes. Berkat penemuannya ini Descartes mengambil peran yang besar dalam menggabungkan aljabar dan geometri. Hasil penemuan descartes, koordinat cartesius ini sangat berpengaruh dalam2 2 Matematika Ekonomi, Bisnis, Josep Bintang Kalangi, Edisi 4, Salemba 4, hlm 41-42 https://www.sheetmath.com/2018/01/pengertian-fungsi-dan-manfaat-koordinat.html 3 perkembangan geometri analitik, kalkulus, dan kartografi.3 Awal pemikiran dasar penggunaan sistem ini dikembangkan pada tahun 1637 dalam dua tulisan karya Descartes. Dalam karyanya Descartes Discourse on Method, ia memperkenalkan saran baru untuk menggambarkan posisi titik atau obyek pada sebuah permukaan. Cara tersebut dengan mengggunakan dua sumbu yang saling tegak lurus antar satu dengan yang lain. Dalam karya berikutnya, La Géométrie, ia memperdalam konsep-konsep yang telah dikembangkannya. Berikutnya baru diperkenalkan untuk sistem-sistem koordinat lain seperti sistem koordinat polar. CONTOH : Bidang Cartesius dengan Empat Kuadran Gambar 3.1 Bidang Cartesius dengan Empat Kuadran 3 https://www.sheetmath.com/2018/01/pengertian-fungsi-dan-manfaat-koordinat.html D. FUNGSI DENGAN SATU VARIABEL BEBAS Fungsi dengan satu variabel bebas dapat diartikan hanya satu variabel bebas yang memengaruhi pada satu variabel terikatnya Fungsi dengan satu variabel bebas ini dapat dikembangkan lagi menjadi beberapa jenis fungsi. Tetapi, jenis-jenis fungsi yang biasanya digunakan atau diterapkan dalam ekonomi dan bisnis hanya terbatas pada beberapaj enis fungsi, yaitu: fungsi polinom, fungsi eksponen, fungsi logaritma. Fungsi polinom sering disebut sebagai fungsi aljabar, sedangkan fungsi eksponen dan logaritma sering disebut sebagai fungsi non-aljabar. Fungsi polinom mempunyai bentuk umum : Y = a0 + a1 X + a2 X2 + . . . + an Xn Di mana : Y = Variabel terikat (dependent) X = Variabel bebas (independent) a0, a1,a,. . . an = konstanta. Konstanta an tidak sama dengan nol dan nonnegative. N menyatakan pangkat dari variabel X dan merupakan bilangan bulat positif. Fungsi polinom ini dapat meliputi : fungsi konstanta fungsi linier, fungsi kuadrat, fungsi pangkat tiga (kubik), dan seterusnya sampai pada fungsi pangkat n (n=1, 2, 3, . . .) E. FUNGSI DENGAN DUA ATAU LEBIH VARIABEL BEBAS Fungsi dengan dua atau lebih variabel bebas adalah suatu fungsi yang menyatakan bahwa terdapat dua atau lebih variabel bebas yang mempengaruhi