2-KINETIKA-REAKSI-POLIMERISASI-RANTAI

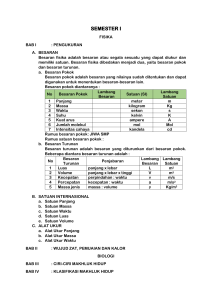
TAHAP POLIMERISASI
1. Inisiasi rantai
2. Propagasi/pertumbuhan rantai
3. Terminasi rantai
Inisiasi menyangkut pembentukan spesies aktif. Inisiasi
dapat dilakukan melalui mekanisme:
• Radikal bebas
• Ionik
• Koordinasi
Mekanisme inisiasi akan membedakan proses
polimerisasi.
Inisiasi polimerisasi radikal bebas dapat dilakukan
dengan beberapa cara:
• Pemanasan monomer
• Penambahan inisiator yang akan membentuk radikal
bebas ketika dipanaskan atau di-radiasi.
Contoh inisiator adalah benzoyl peroksida.
Ketika dipanaskan, ikatan tunggal O – O yang tak stabil
akan terpecah dan dihasilkan dua radikal, masingmasing memiliki satu elektron yang belum berpasangan.
TAHAP-TAHAP INISIASI:
1. Disosiasi homolitik inisiator (I) yang menghasilkan
sepasang radikal R
kd
I  2 R
(1)
• Dengan kd adalah konstanta laju reaksi dekomposisi
inisiator pada temperatur tertentu.
• Nilai kd biasanya berkisar antara 10-4 sampai 10-6 s-1.
• Karena berasal dari inisiator, maka R disebut
sebagai radikal inisiator atau radikal primer.
2. Adisi radikal R pada molekul monomer:
ki
R + M  RM
(2)
dengan RM adalah monomer-ended radical yang
terdiri dari satu unit monomer R sebagai gugus ujung.
Untuk monomer vinyl, tahap kedua ini meliputi
pembukaan ikatan  untuk membentuk radikal bebas:
H
H
R + H2C  C
R  CH2  C
X
X
(3)
Karena setiap molekul inisiator I terdekomposisi menjadi
2 radikal R, maka laju pembentukan radikal (pers. 1):


dR 
 2k
dt
d I
(4)
Setiap R dengan cepat akan menyerang molekul monomer M menghasilkan satu rantai radikal RM.
Dekomposisi inisiator (reaksi 1) jauh lebih lambat daripada reaksi inisiasi (reaksi 2), sehingga langkah ini
merupakan langkah yang mengontrol laju reaksi (rate
controling step).
Jika semua radikal primer (R) bereaksi dengan
monomer, maka laju reaksi inisiasi rantai, Ri, sama
dengan laju pembentukan radikal:
 
 d M
Ri  
 dt
 

M  2 kd I

k
R
i

i
(5)
Tidak semua radikal primer bereaksi dengan monomer.
Ada beberap reaksi yang mungkin terjadi; salah satu
contoh adalah sbb.:
Jika hanya sebagian dari inisiator yang bereaksi dengan
monomer, maka pers. (5) dimodifikasi menjadi:
 
 d M
Ri  
 dt
  2 f kd I
i
(6)
dengan f adalah efisiensi inisiator atau efesiensi inisiasi
yang menyatakan fraksi dari radikal primer R, yang
sebenarnya berkontribusi terhadap inisiasi rantai.
kp
RM
+ M  RM2
RM2
kp
RM3
kp
RM3
RM3
+ M 
+ M 
H
RMn-1
+ M  RMn
(7)
H
R  CH2  C + H2C  C
X
kp
X
H
H
R  CH2  C  CH2  C
X
X
Diasumsikan bahwa reaktivitas radikal tidak tergantung
pada panjang rantai, sehingga semua tahap propagasi
dapat dikarakterisasi dengan menggunakan konstanta
laju reaksi yang sama, yaitu kp.
Laju reaksi propagasi overall dapat dinyatakan dengan:
 
Rp  k p M M
(7)
dengan [M] : konsentrasi monomer
[M] : konsentrasi radikal rantai dengan ukuran
RM dan yang lebih besar
• Untuk kebanyakan monomer, nilai kp berkisar antara
102 – 104 L/mol.s.
• Nilai ini jauh lebih besar jika dibandingkan dengan
konstanta laju reaksi polimerisasi kondensasi (10-3
L/mol.s untuk poliesterifikasi dengan katalis asam).
• Pertumbuhan radikal rantai berlangsung dengan sangat
cepat.
Ada 2 mekanisme:
1. Terminasi dengan kombinasi/coupling yang terjadi jika
dua radikal bergabung membentuk ikatan kovalen.
ktc
RMn + RMm  RM(n+m) R


ktc disebut konstanta laju reaksi kombinasi
(8)
2. Terminasi dengan disproporsionasi yang terjadi jika dua
radikal bergabung membentuk dua molekul baru.
ktd
RMn + RMm  RMm + RMn


(9)
ktd disebut konstanta laju reaksi disproporsionasi.
Reaksi terminasi juga dapat terjadi melalui mekanisme
gabungan antara coupling dan disproporsionasi.
Karena kedua reaksi menghasilkan molekul polimer mati
(tanpa pusat radikal), maka langkah terminasi dapat
dinyatakan dengan:
kt

Mn  Mm
 dead polymer
(10)
dengan kt adalah konstanta laju terminasi overall:
kt  ktc  ktd
(11)
Laju reaksi terminasi:
 
 2
Rtd  2 ktd M 
 2
Rtc  2 ktc M
1. Menurut pers. (8):
2. Menurut pers. (9):
(11)
(12)
3. Menurut pers. (10):
 
 2
Rt  2 kt M
 
 2 ktc  ktd  M
 2
(13)
dengan [M] adalah konsentrasi total radikal rantai.
Angka 2 muncul karena untuk setiap reaksi terminasi
ada 2 radikal yang hilang.
Nilai kt (baik ktc maupun ktd) biasanya berkisar antara
106 – 108 L/mol.s.
Polimerisasi rantai radikal dimulai ketika inisiator mulai
terdekomposisi menurut pers. (1) dan konsentrasi radikal,
[M], yang semula nol menjadi bertambah.
Laju terminasi atau penghilangan radikal yang sebanding
dengan [M]2, mula-mula = 0, dan semakin lama semakin
besar, hingga suatu saat sama dengan laju pembentukan
radikal.
Konsentrasi radikal di dalam sistem menjadi konstan.
Kondisi ini digambarkan sebagai “asumsi steady-state”:
Ri = Rt
dan
d[M]/dt = 0
(14)
Substitusi pers. (14) ke (13) menghasilkan:
 
 
12
 Ri 
(15)

M  
 2 kt 
Karena monomer bereaksi dalam reaksi inisiasi (pers. 2)
dan propagasi (pers. 7), maka laju penghilangan monomer,
yang sama dengan laju polimerisasi, dapat dinyatakan
dengan:
 2
Ri  2 kt M
atau

d M 
(16)

 Ri  Rp
dt
Apabila polimer hasil memiliki panjang rantai rata-rata
yang besar, maka jumlah molekul monomer yang terpakai
pada reaksi inisiasi jauh lebih kecil daripada yang terpakai
pada reaksi propagasi.
Untuk perhitungan, Ri dapat diabaikan, sehingga laju
polimerisasi dapat dianggap sama dengan laju propagasi
(long-chain approximation) :
d M

 Rp  k p M M
dt
 
(17)
Konsentrasi radikal sangat rendah ( 10-8 mol/L) sehingga
sulit diukur. Oleh karena itu [M] dieliminasi dengan cara
disubstitusi dengan pers. (15):
 Ri 
d M


 Rp  k p M
dt
 2 kt 
12
(18)
Jika inisiasi terjadi akibat dekomposisi termal inisiator
(pers. 1), maka substitusi pers. (6) ke pers. (18) menghasilkan:
 f kd I 
d M


 Rp  k p M
dt
 2 kt 
12
(19)
Pers. (18) dan (19) menunjukkan bahwa laju polimerisasi
tergantung pada konsentrasi monomer dan akar dari laju
inisiasi.
Jika reaksi dekomposisi inisiator merupakan reaksi unimolekular, maka reaksi dekomposisi merupakan reaksi
order satu:
d I

 kd I
dt
(20)
t
d I
 
 kd  dt
I0 I
0
I
I
 ln
 kd t
I0
I  I0 e  kd t
(21)
Half life (waktu paruh) didefinisikan sebagai waktu yang
diperlukan bagi suatu senyawa untuk bereaksi hingga
jumlahnya tinggal setengahnya.
Ini dapat diperoleh dengan cara mengintegralkan pers.
(20) antara [I]0 pada t = 0 sampai [I] = [I]0/2 pada t = t1/2
I0 2 d I
 
I0
I
t1 2
 kd  dt
ln 2
t1 2 
kd
0
I0 2
 ln
 kd t1 2
I0
(22)
Karena Half life tidak tergantung pada konsentrasi, maka
t1/2 digunakan sebagai kriteris aktivitas inisiator.
Substitusi pers. (21) ke (19) menghasilkan:
12

d M   f kd  
  MI10 2 e  kd t
Rp  
 kp 
dt
  kt  

(3)
 kd t
R

e
(1) p

(2)
2

(1)
2
Laju reaksi semakin lama semakin turun secara
eksponensial karena inisiator semakin lama
semakin banyak yang digunakan.
(23)
12
(2) Rp  MI0
• Di awal reaksi, [I]  [I]0.
• Hasil eksperimen menunjukkan bahwa di awal
reaksi Rp bervariasi dan berbanding lurus dengan
[I]1/2 pada [M] konstan.
• Jika [I] dan [M] bervariasi, maka plot antara Rp
vs. [M] [I]1/2 akan berupa garis lurus.
Rp vs. [M] [I]1/2 untuk polimerisasi yang melibatkan methyl
methacrylate dan styrene
(3) Rp  k p  f kd 
 kt 
12
Rp 
kp
kt1 2
• Polimerisasi radikal terhadap ethylene pada 130C
dan tekanan 1 bar, nilai dari kp/kt1/2 hanya 0,05
• Hal ini berarti bahwa terminasi jauh lebih cepat
daripada propagasi  tidak akan diperoleh
polimer.
• Pada 200C dan tekanan 2500 bar, kp/kt1/2 = 3 
propagasi lebih cepat daripada terminasi  akan
diperoleh polimer.
• Tanpa adanya katalis, ethylene tak dapat
dipolimerisasi pada tekanan rendah.
Pers. (23) dapat juga ditulis sebagai:
d M  k p 

  1 2   f kd I0 1 2 e  kd t
M  kt 

2
dt
(24)
Integrasi pers. (24) antara [M]0 pada t = 0 sampai [M]
pada t:
M  k p   f I0 

 ln
 2  1 2  
M0  kt   kd 
12
1  ek t 2 
d
(25)
Extent of monomer conversion, p, atau konversi
didefinisikan sebagai:
M0  M
p
M
(26)
M
1  p  
M0
(27)
Substitusi pers. (27) ke (25) menghasilkan:
 k p   f I0 

 ln1  p   2  1 2  
 kt   k d 
12
1  ek t 2 
d
(28)
Pers. (28) dapat pula ditulis sebagai:
12

 f 
 I10 2 1  e  kd t
p  1  exp  2k p 

 kd kt 

2




(29)
Untuk reaksi yang dilangsungkan dalam reaktor batch,
konversi maksimum dapat diperoleh dengan mamasukkan t =  pada pers. (29) :
12


 f 
12
 I0 
p  1  exp  2k p 


 kd kt 
(30)
Per. (30) menyatakan bahwa reaksi batch selalu menyisakan monomer.
CONTOH 1
Dekomposisi benzoyl peroksida dikarakterisasi dengan
waktu paruh 7,3 jam pada 70C dan energi aktivasi 29,7
kkal/mol. Berapa konsentrasi (mol/L) peroksida yang
diperlukan untuk mengkonversi 50% dari jumlah mulamula monomer vinyl menjadi polimer dalam waktu 6 jam
pada 60C? (Data: f = 0,4; kp2/kt = 1,04  10-2 L/mol.s pada
60C).
PENYELESAIAN
ln 2
t1 2 
kd
kd 70

ln 2
ln 2


 2,638  10 5 s
t1 2 7,3  3600 s
kd  Ad e Ed
RT
Ed
ln kd  ln Ad 
RT
kd 60 Ed  1
1 
ln
 


kd 70
R  333 343 
ln
kd 60
2,638  10 5
29,7  103 kal mol-1  1
1 




-1 -1 
1,987 kal mol K  333 K 343 K 
kd 60  7,128  106
s-1
Untuk konversi 50%:
 k p   f I0 

 ln1  p   2  1 2  
 kt   k d 
I0 
1 2
I0 
1 2
12
1  ek t 2 
d
 kp   f 
2
 1 2   

 ln1  p   kt   kd 

12
2

1,04  10 2
 ln1  0 ,5 
1  e 

 7 ,128106  63600  2
[I]0 = 3,75  10-2 mol/L

1  ek t 2 
d

12
0 ,4



6 
 7,128  10 
12
CONTOH 2
Konversi sebesar 50% untuk suatu monomer baru yang
mengalami polimerisasi dalam larutan homogen dengan
inisiator termal dicapai dalam waktu 500 menit. Berapa
waktu yang diperlukan untuk mencapai konversi 50% jika
semua kondisi yang sama kecuali bahwa konsentrasi
inisiatornya 4 kali lipat?
PENYELESAIAN
Jika 1  e
 kd t 2
dijelaskan di belakang
 kd t 2
maka pers. (28) menjadi
 k p   f I0 

 ln1  p   2  1 2  
 kt   k d 
12
 kd t 


 2 
 f kd 

 ln1  p   k p 
 kt 
12
I10 2 t
Jika temperatur sama, maka harga kp, kd, dan kt konstan.
 ln1  p   K I10 2 t
 ln1  p1   K I10 ,21 t1
(a)
 ln1  p2   K I10 ,22 t2
(b)
p1 = 0,5
[I]0,1
t1 = 500 menit
p2 = 0,5
[I]0,2 = 4 [I]0,1
t2 = ?
Jika pers. (a) dibandingkan dengan pers. (b):
12
 ln1  p1  I0 ,1 t1
 12
 ln1  p2  I0 ,2 t2
 I0 ,1 

1  



I
 0 ,2 
12
 t1   1 
   
 t2   4 
t2  0,5 t1  250 menit
12
 t1 
 t1 
   0 ,5  
 t2 
 t2 
EKSPANSI
e
f x


 f  x i
i 0
i!
 1  f x 
 f  x 2  f  x 3
2!
2
e  kd t

3!
3

  kd t    kd t 

 

k
t
2
 1    d    2    2   
2!
3!
 2 
e  kd t
2
3




k
t
k
t
k
t
kd t
2
d
d
d
 1


 1
2
8
48
2
1e
 kd t 2
kd t

2
CONTOH 3
Jika larutan 5% monomer A yang mengandung 10-4 mol/L
peroksida P dipolimerisasi pada 70C, maka konversi
sebesar 40% akan dicapai dalam waktu 1 jam. Berapa
waktu yang diperlukan untuk mem-polimerisasi 90% dari
monomer yang semula dimasukkan ke dalam larutan
dengan konsentrasi 10% dan mengandung peroksida P
sebanyak 10-2 mol/L?
PENYELESAIAN
Jika 1  e  kd t 2  kd t 2
maka pers. (27) menjadi
 f kd 

 ln1  p   k p 
 kt 
12
I10 2 t
Jika temperatur sama, maka harga kp, kd, dan kt konstan.
 ln1  p   K I10 2 t
12




I
ln1  p1 
0 1 t1

ln1  p2  I0 12 2 t2
12




I


ln 1  p2
0 1 t1
t2 
ln1  p1  I0 12 2


4 1 2
1
ln1  0 ,9  10
t2 
 0 ,45 jam
1
2
ln1  0 ,4  10 2

