BAB I

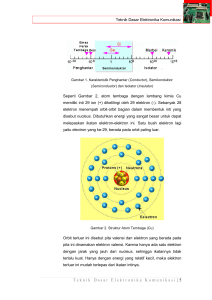
BAB IV. SIFAT PARTIKEL DARI GEL0MBANG
Partikel dan gelombang merupakan dua konsep yang berbeda tetapi dari
pengalaman sehari-hari tenyata ada sesuatu yang misterius. Dari kedua hal tersebut terdapat hal-hal yang tidak dapat dijelaskan dengan menggunakan konsep
atau hukum fisika yang telah ditemukan terdahulu (klasik). Analisis kedua gejala
tersebut merupakan awal dari kata fisika modern yaitu sifat dualitas partikel gelombang. Kita akan memulai bahas topik dualitas partikel gelombang. Pembahasan sifat partikel gelombang yaitu radiasi elektromagnet atau dalam kondisi tertentu gelombang elektromagnet dapat memiliki sifat seperti partikel. Sifat gelombang
partikel dalam hal ini yang kita bahas adalah elektron. Karena elektron dalam kondisi tertentu mempunyai sifat seperti gelombang.
Munculnya teori kuantum (cahaya) diawali dari usaha menerangkan radiasi
panas dari benda-benda bersuhu tinggi berdasarkan teori mekanika statistik klasik.
Muatan yang bergerak dipercepat akan memancarkan gelombang elektromagnet.
Radiasi panas semacam radiasi elektromagnet yang dipancarkan oleh benda-benda
karena suhunya.
A. Photon dan Efek Foto Listrik
Photon merupatan bentuk materi dari cahaya atau gelombang elektromagnet.
Photon dianggap sebagai partikel (materi) tanpa massa diam (mo = 0).
1. Teori Kuantum Cahaya
Energi dan momentum photon dihubungkan dengan frekuensi dan panjang
gelombang dinyatakan oleh bentuk
h
E = hf dan p =
1

Persamaan (1) menyatakan E energi satuan joule f frekuensi hertz p momentum
kg ms-1, λ panjang gelombang meter dan h tetapan Planck 6,626 .10-34 Js atau
4,14 .10-15 eVs (Max Planck 1858 - 1947). Dalam dinamika terdapat hubungan
E
hf
f
1
p = (c kelajuan cahaya) p =
dan
= . Besaran tersebut memenuhi huc
c
c

bungan dengan persamaan (1).
Konsep photon hanya digunakan dalam interaksi radiasi elektromagnet dan
partikel bermuatan atau interaksi radiasi elektromagnet dengan materi (bukan inter
44
aksi dengan elektron bebas). Dengan demikian interaksi gelombang elektromagnet dengan elektron atau partikel bermuatan lain di dalam proses berhubungan
dengan photon sejumlah energi dan momentum dapat saling bertukar.
Contoh 1.
Berapakah energi dan momentum sebuah photon cahaya merah (λ 650 nm) ?
Berapakah panjang gelombang photon yang berenergi 2,4 eV ?
Penyelesaian menggunakan persamaan (1)
hc
(4,14 .10 15 eVs)(3 .108 ms 1 )
E=
=
= 1,91 eV = 3,06 .10-19 J
9

650 .10 m
15
h
(4,14 .10 eVs)
p=
=
= 1,91 eV c-1 = 3,06 .10-19 J c-1
9

650 .10 m
hc
h
(4,14 .10 15 eVs)(3 .10 8 ms 1 )
λ =
=
=
= 517 n m = 517 .10-9 m
2
,
4
eV
E
p
2. Efek Foto Listrik
Peristiwa foto listrik terjadi pada permukaan logam yang disinari (berkas
cahaya) ke luarlah sejumlah elektron dari permukaannya. Prinsip dasar yang perlu
diketahui dalam masalah radiasi dan penyerapan energi gelombang elektromagnet
dalam atom (dapat molekul, inti) adalah atom tersebut hanya dapat mengeluarkan
atau menyerap energi radiasi gelombang elektromagnet hanya pada frekuensi tertentu. Energi atom (mungkin molekul) terkuantisasi dan hanya memiliki nilai tertentu. Seandainya ada atom dalam keadaan mantap energi E menyerap radiasi
gelombang elektromagnet frekuensi f dan sesudahnya ia memiliki kemantapan
lain dengan energi lebih tinggi E!. Perubahan energi atom E! - E dan pada sisi lain
energi photon yang diserap hf. Hukum kekekalan energi kedua hal tersebut sama
sehingga
E! - E = hf
2
Persamaan (2) disebut formula Bohr pertama kali disampaikan oleh ahli fisika
berkebangsaan Denmark (Niels Bohr 1885 - 1962) pada tahun 1913. Persamaan
(2) menyatakan apabila atom melepaskan photon atau energi mantapnya berubah
dari E! menjadi E dan energi sisanya sebagai energi gelombang (hf).
Konsep photon digunakan pada seluruh proses interaksi gelombang elektromagnet dengan materi. Salah satu contoh gambaran konsep photon adalah peristi-
45
wa efek foto listrik. Gagasan tentang efek foto listrik ditemukan oleh Heinrich
Hertz (1857 - 1894) pada tahun 1887 dalam suatu percobaan tentang perambatan
Gelombang elektromagnet. Hertz melakukan pengamatan, penyinaran dengan sisinar
nar ultraviolet pada elektroda. Wilhelm Hallwachs (1859 -
Na
1922) melakukan pengamatan emisi listrik karena penyinaran
pada logam Zn, Rb, K dan Na. Peristiwa munculnya arus
elektrometer
Gambar 1
listrik atau lepasnya elektron dari logam disebut dengan gejala efek foto listrik.
Percobaan, cara untuk menunjukkan adanya peristiwa efek fotolistrik. Permukaan logam disinari (cahaya) dan dihubungkan dengan elektrometer yang telah
bermuatan negatif (gambar 1). Akibat penyinaran keping elektrometer mula-mula
menyempit akhirnya membuka kembali (artinya sekarang elektrometer bermuatan
positif berlawanan dengan muatan awal). Hal tersebut terjadi karena penyinaran
membebaskan elektron (logam menjadi bermuatan positif atau logam menjadi ion
posirif).
Aliran elektron (arus listrik) tersebut (dalam
Anoda
percobaan) terus bertambah seiring bertambahnya
intensitas cahaya yang dijatuhkan pada permuka-
Katoda
A
Gambar 2
an logam. Namun demikian terdapat frekuensi ter
kecil (frekuensi ambang fo) cahaya yang tidak
menghasilkan peristiwa foto elektron. Pancaran arus elektron mempunyai energi
kinetik maksimum semakin besar jika panjang gelombang cahaya yang digunakan
I
semakin pendek (frekuensi semakin besar). Tidak
b
seluruh panjang gelombang menghasilkan pancara
an arus elektron. Panjang gelombang terbesar sinar penghasil fotoelektron λo (harga λo disebut nilai ambang harga paling besar dapat menghasil-
Φo
Gambar 3.
V
kan arus elektron un tuk seterusnya sinar-sinar
penghasil fotoelektron nilai panjang gelombang-
nya < λo).
Lepasnya elektron dari atom (mungkin dari molekul) sehubungan dengan pe
46
nyerapan energi tertentu (Φo) oleh logam. Bila elektron menyerap energi dari caha
ya E = hf sehingga sisa energi dijadikan energi kinetik (Ek) oleh elektron
Ek = E - Φo
3
Bila E energi cahaya (E < Φo) pada logam tidak akan terjadi pancaran elektron.
Tidak setiap elektron logam dapat lepas memerlukan energi Φo (fungsi kerja) yang sama. Akan tetapi setiap mengganti logam (dalam percobaan) diperoleh
grafik gambar (4) selalu sejajar dengan nilai Vo berbeda (nilai tersebut berhubungan dengan fungsi kerja setiap logam). Koefisien arah grafik merupakan nilai
tetapan Planck.
Vo
Energi terkecil untuk melepaskan elektron
2,35
dari permukaan logam disebut fungsi kerja (Φo)
a
logam yang bersangkutan (nilai terkecil agar elek
tron lepas dari permukaan logam adalah hfo = Φo
0,72
c
Vo
6
b
10
=
f
Gambar 4
hc
). Dengan demikian Ek maksimum dari peo
nyinaran cahaya yang memiliki frekuensi f
Ekm = hf - Φo atau Ekm = hf - hfo
4
Persamaan (4) h adalah tetapan Planck. Besarnya Ekm dari arus elektron dapat ditunjukkan dengan menempatkan potensial penghalang (Vo) agar arus elektron ber
henti dalam tabung sehingga terjadi hubungan
eVo = hf - hfo atau Φo = e Vo
5
Persamaan (5) jika dibuat grafik energi vs frekuensi berupa garis lurus (h tetapan
planck sebagai koefisien arah).
Pengukuran potensial penghalang dapat dilakukan dengan gambar (2). Beda
tegangan anoda-katoda diperbesar arus menjadi semakin kecil (pembacaaan ampe
remeter menurun menuju nol). Tegangan yang bersangkutan disebut potensial
penghalang (potensial henti Vo). Pengukuran Vo merupakan cara untuk menentukan Ekm elektron (cara menentukan fungsi kerja logam Φo = e Vo).
Dengan memperhatikan hubungan (f, v dan λ gelombang) persamaan (4) dapat pula ditulis sebagai bentuk
1
1
Ekm = h c (
) = ½ m v2

o
47
Tabel, fungsi kerja (Φo dalam elektronvolt) fotolistrik beberapa logam
No.
logam
lambang
Φo
logam
lambang
Φo
1.
cesium
Cs
1,9 eV
kalsium
Ca
3,2 eV
2.
kalium
K
2,2 eV
tembaga
Cu
4,5 eV
3.
natrium
Na
2,3 eV
perak
Ag
4,7 eV
4.
litium
Li
2,5 eV
platina
Pt
5,6 eV
Hasil percobaan efek fotolistrik dapat disimpulkan sebagai berikut
1. Arus fotolistrik bertambah bila intensiats cahaya yang digunakan bertambah.
2. Ekm elektron fotolistrik tidak dipengaruhi oleh intensitas cahaya yang di
gunakan
3. Ekm bertambah jika frekuensi cahaya yang digunakan lebih besar (naik)
4. Setiap logam memiliki frekuensi ambang (fo) sendiri-sendiri. Jika ada
cahaya memiliki frekuensi < fo tidak akan mampu melepaskan fotoelektron (efek foto listrik tidak terjadi).
Elektron yang berada jauh di bawah permukaan logam dibutuhkan energi > Φo (be
berapa diantaranya ke luar dengan Ek yang lebih rendah). Sebuah photon yang me
masok energi sebesar Φo (energi yang tepat untuk melepaskan sebuah elektron)
berkaitan dengan panjang gelombang ambang λo. Panjang gelombang tersebut tidak memiliki kelebihan energi yang tersisa bagi Ek fotoelektron sehingga persama
an (4) disederhanakan menjadi
Φo = hf sehingga λo =
hc
o
6
Contoh 2.
Carilah Ek foto elektron jika sinar ultraviolet dengan panjang gelombang
3500 Å jatuh pada permukaan kalium !
Penyelesaian menggunakan persamaan (4).
Persamaan (4) Ek = hf - Φo atau Ek =
hc
- Φo

3 .10 m s 1
Dengan demikian Ek = (4,14 .10-15 eV s)
- 2,2 eV = 1,3 eV
3500 .10 -10 m
Contoh 3.
Suatu percobaan mengasilkan grafik gambar (4). Sumbu mendatar frekuensi
48
(dinyatakan dalam 1014 Hz), sumbu vertikal dinyatakan dalam volt. Berapakah
nilai h (tetapan Planck) dalam percobaan tersebut ? Seandainya nilai Vo logam tersebut berhubungan dengan frekuensi 4,3 .1014 Hz. Berapakah nilai fungsi kerja
dari logam yang bersangkutan yang digunakan.
Penyelesaian menggunakan persamaan (4)
Ek dinyatakan dalam eV sehingga persamaan (4) menjadi eVo = hf - hfo.
Vo
h
h
Potensial penghalang Vo =
(f - fo) atau
=
dengan grafik gambar
e
e
f  fo
(4) dihasilkan bentuk Vo = garis ab dan f - fo = garis bc sehingga
(2,35  0,72) V
h
=
= 4,1 .10-15 Vs atau h = 1,6 .10-19 C (4,1 .10-15 Vs)
e
10 14 (10  6 )
Hasil nilai tetapan Planck menjadi h = 6,56 .10-34 J s.
Φo = hfo = (6,63 .10-34 Js)(4,3 .1014 Hz) = 2,9 .10-19 J atau 1,8 eV
Contoh 4.
Fungsi kerja logam tungsten 4,52 eV. Berapakah panjang gelombang ambang tungsten ? Berapakah Ekm elektron yang dipancarkan apabila digunakan radiasi dengan panjang gelombang 200 nm ? Berapakah potensial henti kasus ini ?
Penyelesaian menggunakan persamaan (4, 5 dan 6)
hc
1240 eV nm
λo =
=
= 274 nm (berada pada daerah ultraviolet)
o
4,52 eV
hc
1240 eV nm
Ekm = hf - Φo =
- Φo =
- 4,52 eV = 1,68 eV
200 nm

Ek m
1,68 eV
Vo =
=
= 1,68 V
e
e
C. Sinar Rǒentgen (Sinar X).
Gejala sinar Roentgen (sinar x) merupakan gejala kebalikan dari efek fotolistrik. Elektron dipercepat (diberi medan listrik) lalu dihentikan oleh logam (sasar
an tumbukan) Ek elektron menjadi nol (diam) dan energi tersebut diubah menjadi
energi gelombang (sinar x).
1. Produksi Sinar X.
Dalam tabung hampa udara (tekanan udara kecil) ditempatkan logam sebagai sasaran (anoda) ditembaki dengan elektron (berasal dari katoda) menghasilkan sinar yang tidak tampak. Interaksi elektron dengan logam sasaran terebut
itulah yang menghasilkan radiasi sinar.
Radiasi sinar yang tidak tampak tersebut
49
pertama kali ditemukan oleh Wilhelm Konrad von Roentgen (1895) ahli fisika ber
kebangsaan Jerman hidup antara tahun 1845 - 1923
sinar x
Radiasi sinar Roentgen pada saat itu cukup misterius sehingga dinamakan juga si
A
e
K
nar x. Sinar x memiliki sifat antara lain
- dapat menyebabkan beberapa logam
berpendar (misal ZnS)
Gambar 5
- memiliki daya tembus yang cukup besar
(dapat menembus beberapa logam dan zat-zat lain
- dapat menghitamkan (merusak) film fotografi.
- sinar x merupakan gelombang elektromagnet dengan gelombang sangat pendek
(hanya beberapa 10-10 m)
- dapat merusak dan menembus jaringan tubuh
- merambat lurus (tidak dibelokkan oleh medan listrik maupun magnet)
Sifat sinar x tersebut semakin kuat bila elektron yang menumbuk sasaran semakin kuat (cepat) dan semakin besar jumlah elektronnya akan semakin besar juga intensitasnya. Radiasi sinar x terjadi apabila elektron yang bergerak dipercepat
lalu menumbuk sasaran (anoda atau dihentikan) radiasi yang muncul merupakan
radiasi pengereman atau bremstrahlung.
Percobaan dilanjutkan dengan cara mengubah-ubah logam sasaran (anoda)
yang dijadikan sasaran tumbukan elektron misal molybdenum memunculkan grafik spektrum yang dijelaskan menggunakan teori elektromagnet. Panjang gelombang sinar x minimum memiliki hubungan antara beda potensial anoda-katoda (V)
Secara eksperimen Duane dan Hunt merumuskan hubungan sebagai
1,24 .10 6 V m
λmim =
V
Contoh 5.
7
Mesin penghasil sinar x menghasilkan spektrum dengan panjang gelombang
minimum 0,1 A. Berapakah beda potensial pemercepat elektron (beda potensial
anoda-katoda) yang digunakan agar menghasilkan panjang gelombang dalam nilai tersebut ?
Penyelesaian menggunakan persamaan (7)
50
1,24 .10 6 volt m
= 1,24 .105 volt
11
10 m
Beda potensial mesin tersebut yang digunakan untuk mempercepat elektron nilai-
V =
nya adalah 1,24 .105 volt.
Panjang gelombang minimum tersebut berhubungan dengan energi kinetik
maksimum foton sinar x tersebut Ek = eV = h υmak.
hc
Ek = h fmak =
 mim
Contoh 6.
8
Dari contoh soal nomor lima tentukan frekuensi maksimumnya !
Penyelesaian menggunakan persamaan (8)
Frekuensi maksimum terjadi jika λ minimum karena, kecepatan c tetap sec
3 .10 8 m s 1
hingga fmak =
=
= 3 .1019 s-1 = 3 .1019 Hz
 mim
10 11 m
2. Difraksi Sinar x
Willian Henry Bragg 1862 - 1942 W. Lawrence Bragg 1890 - 1971 meng
analisis λ sinar x dihitung dengan menggunakan cara difraksi kisi kristal (ideal).
Misal sinar x datang pada deretan atom dengan sudut θ serta jarak antar atom d
sehingga selisih perjalanan dua sinar tersebut 2 d Sin θ. Apabila interferensi sinar
saling memperkuat panjang gelombang sinar x dihitung dengan cara difraksi
2 d Sin θ = n λ
9a
Persamaan (7a) n menyatakan orde sinar terhambur. Sebaliknya dengan menggunakan per-
.
.
.
.
d.
.
.
θ .
Gambar 6
.
.
.
.
.
samaan (9a) kita dapat menghitung jarak antar
.
.
atom dari kristal jika panjang gelombang berkas sinar x terhambur diketahui.
Jika interferensi gelombang saling memperlemah bentuk persamaan (9a)
menjadi
2 d Sin θ = (n + ½ ) λ
9b
Contoh 7.
Jarak atom-atom Ca 3 .10-10 m. Apabila sinar x didatangkan pada kristal
tersebut dengan sudut 2,8o. Interferensi saling memperkuat terjadi pada orde per-
51
tama tentukan panjang gelombang sinar x yang digunakan !
Penyelesaian menggunakan persamaan (9)
Persamaan (9) menghasilkan 2 (3 .10-10 m) Sin 2,8o = (1) λ sehingga
menghasilkan nilai λ = 3 .10-11 m atau λ sinar x adalah 0,3 Ao.
3. Produksi Pasangan.
Gejala lain interaksi sinar x dengan materi adalah produksi pasangan elektron (e- atau - 1,6 .10-19 C) dan positron (e+ atau 1,6 .10-19 C). Dalam gejala foto
listrik ada kemungkinan sebuah photon menyerahkan sebagian atau seluruh energinya pada elektron. Atau mungkin photon berubah menjadi sebuah elektron dan
sebuah positron suatu proses perubahan energi elektromagnet menjadi energi diam. Gejala ini akan terjadi bila energi photon sinar x yang digunakan ≥ 2 mo c2
(dengan mo adalah massa diam elektron besar 9,1 .10-31 kg atau 0,51 MeV).
Dengan demikian produksi pasangan akan terjadi jika energi photon ≥ 1,02 MeV
atau bersesuaian dengan panjang gelombang λ = 0,012 Ao. Gelombang elektromagnet dengan λ = 0,012 Ao disebut sinar gamma (). Sinar γ di alam sebagai pan
caran inti radioaktif dan dalam sinar kosmik.
Kelebihan energi photon tersebut dijadikan energi kinetik elektron dan positron h f = E + + E -.
h f = (me c2 + Ek +) + (me c2 + Ek -)
10
Nilai besaran Ek+ dan Ek – selalu positif sehingga photon harus memiliki energi
serendah-rendahnya 2 me c2 = 1,02 M eV. Proses ini dapat terjadi photon harus
berada pada daerah sinar gamma inti atom yang berenergi setinggi itu.
photon → elektron + positron
Positron ditemukan pertama kali oleh Anderson pada tahun 1932 (keberadaannya telah diramalkan oleh P. A. M. Dirac pada tahun 1928. Produksi pasangan
hanya terjadi di bawah pengaruh medan inti.
4. Proses Anihilasi.
Kebalikan dari produksi pasangan terjadi, bila elektron dan positron bertemu
dan lenyap muncul sepasang photon (elektron + positron → photon).
(me c2 + Ek +) + (me c2 + Ek -) = E1 + E2
11
52
Karena nilai Ek+ dan Ek– sangat kecil sehingga positron dan elektron dapat dianggap diam. Sehingga kekekalan momentum mensyaratkan kedua photon memiliki energi sama me c2. Arah photon sedemikian rupa sehingga energi dan momentum liniernya tetap (segaris arah berlawanan).
Proses pelenyapan (anihilasi)
terjadi tidak perlu ada pengaruh medan inti atau partikel lain.
D. Efek Compton
Efek Compton (contoh lain) merupakan interaksi materi dan gelombang. Me
nurut teori kuantum cahaya photon (materi cahaya) berlaku sebagai partikel.
Photon (materi cahaya) tidak memiliki massa diam (mo = 0). Jika hal tersebut
benar sehingga penyinaran dapat dianalisis dengan menggunakan bentuk tumbukan antar partikel. Gambar (7) menunjukkan tumbukan yang dilakukan oleh photon
sinar x (1) menumbuk elektron diam (2). Photon sinar x (1) mengalami hamburan
dari arah semula dengan membuat sudut θ (3) dan elektron yang semula diam terpental dengan sudut φ dari arah horisontal (4) dan bergerak (karena memperoleh
impuls). Dalam tumbukan ini dipandang photon sinar x kehilangan sejumlah energi kinetik dan diberikan pada elektron. Jika photon sinar x (1) berfrekuensi f dan
photon hamburan (3) berfrekuensi f! (dengan anggapan energinya berkurang sehingga f > f!) hilangnya energi photon akan sama dengan energi yang dimiliki
oleh elektron (4) sebagai Ek.
Ek = h f - h f!
12
Energi photon (1) (partikel tidak memiliki massa diam) berenergi E = pc atau
E
hf
h
p=
=
=
.
13
c
c

Dalam tumbukan berlaku hukum kekekalan energi (artinya energi sebelum
tumbukan sama dengan setelah tumbukan) sehingga menjadi
E + mo c2 = E! + mo2 c 4  p42 c 2
14
Hukum kekekalan momentum berlaku momentum sebelum tumbukan dan sesudah tumbukan sama
p1 + p2 = p3 + p4
Dari persamaan (15) diperoleh persamaan momentum arah mendatar
hf
hf !
+ 0 =
Cos θ + p Cos φ
c
c
15
atau
53
p c Cos φ = h f - h f! Cos θ
E! = p3 c
E = h f! (3)
(2) 
p2 = 0 
16a
Momentun arah tegak lurus
!
(1)
E= hf
p1 =
hf
c
moc2
(4)
p4
E= m c  p c
2
o
4
hf !
Sin θ - p Sin φ
c
p c Sin φ = h f! Sin θ
0 =
2
4
atau
16b
θ merupakan sudut hamburan photon, dan φ su2
dut pental (lemparan) elektron.
Gambar 7
Persamaan (16) dikuadratkan serta dijum-
lahkan akan dihasilkan bentuk
(p c)2 = (hf)2 - 2 (hf)(hf!) Cos θ + (hf!)2
17
Energi total E = Ek + mo c2 serta E = m c  p c dengan mengkuadratkan
2
o
4
2
4
2
kedua persamaan tersebur diperoleh Ek2 + 2 (mo c2)(Ek) + (mo c2)2 = mo2 c 4 + p42 c 2
Dalam hal ini p42 c 2 = (p c)2 sehingga (p c)2 = (Ek)2 + 2 (mo c2)(Ek). Persamaan
(12) untuk mengganti Ek sehingga
(p c)2 = (hf)2 - 2 (hf)(hf!) + (hf!)2 + 2 (mo c2)(hf – hf!)
18
Bentuk persamaan (17 = 18) digabungkan akhirnya menjadi
2 (mo c2)(hf – hf!) = 2 (hf)(hf!)(1 - Cos θ)
19
!
!
mc f
f f
f
Persamaan (19) akan menjadi o ( ) =
(1 – Cos θ) atau
c c
c
h c
h
(λ! - λ) =
(1 - Cos θ)
20
mo c
Persamaan (20) diperoleh Arthur Holly Compton (1892 - 1962) pada tahun
1920 akhirnya gejala tersebut dinamakan efek Compton. Gejala ini juga menunh
jukkan bukti pembenar teori kuantum radiasi cahaya. Besaran
disebut panjang
mo c
gelombang Compton (nilai untuk elektron 2,426 .10-12 m). Gejala efek Compton,
dapat pula dipandang sebagai hasil tumbukan partikel berkecepatan tinggi.
Contoh 8.
Sinar X panjang gelombang 24 .10-12 m dihamburkan (secara compton) dan
berkas hamburan teramati dengan sudut 60o (relatif terhadap sinar datang).
Carilah 1. panjang gelombang hamburan sinar X
2. energi photon hamburan sinar X
3. energi kinetik dan arah elektron terlempar
54
Penyelesaian menggunakan persamaan (20)
h
λ! = λ +
(1 - Cos θ) = 24 .10-12 m + 2,426 .10-12 (1 – Cos 60o)
mo c
= 24,12 .10-12 m
hc
1240 eV nm
E! = ! =
= 5141 eV
λ
0 ,2412 nm
1240 eV nm
Ek = E - E! =
- 5141 eV = 5167 eV – 5141 eV = 26 eV
0 ,24 nm
E !Sin
( 5141 eV )( Sin60 o )
tg φ =
=
= 1,715 atau φ = 59o 42!
!
o
E  E Cos
( 5167  5141 ) eV ( Cos60 )
Contoh 9.
Sinar X panjang gelombang 22 .10-12 m atau berenergi 56 keV, ditujukan pa
da karbon serta terjadilah hamburan (sudut hamburan 85o). Berapakah penambahan panjang gelombang Compton ? Berapa presen energi photon awal yang hilang ? Kemana arah gerak elektron hambur !
Penyelesaian menggunakan persamaan (16 dan 20)
6 ,63 .10 34 Js
Persamaan (20) Δλ =
(1 - Cos 85o)
31
8
1
9,11 .10 kg (3 .10 ms )
Perpanjangan gelombang tersebut nilainya Δλ = 2,21 .10-12 m
E  E!
(c /  )  ( c /  !)
 !
hf  hf !
Presentase kehilangan energi
=
=
=
E
c/
hf
!
Pernyataan λ! – λ = Δλ dan λ! = λ + Δλ sehingga prosentasenya hilang menjadi

ή =
21
  
2,21 .10 12 m
Jadi ή =
= 0,091 atau 9,1 %
(22 .10 12  2,21 .10 12 )m
E !Sin
! Sin 85 o
=
E  E !Cos
  ! Cos 85 o
(24,21)(0,995)
(24,21)(10 12 )(0,995)
tg φ =
dan φ = arc tg
12
22  (24.21)(0,087 )
[22  (24.21)(0,087 )](10 )
Dari persamaan (16) dihasilkan bentuk tg φ =
E. Photon dan Gravitasi
Photon dalam situasi tertentu dapat berlaku serupa dengan partikel. Misal
pada proses radiasi atau efek fotolistrik Compton dan lain-lain dengan massa
berupa massa geraknya. Prinsip kesetaraan menyatakan bahwa massa inersial (kelembaman) suatu benda sama dengan massa gravitasinya. Prinsip tersebut diakui
dari suatu kenyataan bahwa dalam percobaan seorang atau pengamat dalam la-
55
boratorium tertutup tidak dapat membedakan antara efek yang dimunculkan oleh
medan gravitasi dan efek yang ditimbulkan oleh percepatan laboratoriumnya.
Perbedaan antara keduanya (jenis massa gravitasi dan lembam) terletak pada
kenyataan bahwa massa kelembaman suatu benda sebagai penentu tanggapan terhadap gaya yang di terapkan sedang massa gravitasi sebagai penentu gaya tarik
gravitasi atau interaksi dengan massa lain. Kedua pemikiran tersebut mengarah
pada kesimpulan bahwa cahaya harus mengalami efek gravitasi. Dari hasil pengamatan, photon ketika bertumbukan berlaku seakan-akan mempunyai masa kelem
baman sebesar (walaupun telah disimpulkan photon tidak memiliki massa diam),
p
hf
hf
m =
= 2 (hal tersebut karena p =
dan untuk photon v = c)
c
v
c
Bukti dari kedua hal tersebut (memiliki kenyataan) antara lain
-
cahaya bintang yang melewati dekat matahari (atau benda dengan massa
masif) dibelokkan 0,0005o. Nilai sebesar itu teramati saat gerhana matahari. Prosedur pengamatan dengan cara membandingkan posisi cahaya
lewat dekat matahari saat gerhana dan tidak saat cahaya lewat tidak dekat matahari.
-
benda massa m dijatuhkan dari ketinggian h dekat permukaan bumi (me
miliki energi gravitasi mgh), akan dipercepat sampai di bumi akan memiliki energi kinetik ½ mv2 atau v =
2 gh . Hal tersebut jika dialami
oleh photon yang jatuh lewat jarak s (manifestasinya photon akan memiliki tambahan energi mgs) dalam bentuk lain yaitu pertambahan frekuensi dari f menjadi f! (pertambahan massa hf/c2 diabaikan) sehingga
hfgs
gs
hf! = hf + mgs = hf +
atau hf! = hf (1 + 2 )
2
c
c
Contoh 10.
22
Berapakah perubahan frekuensi relatif photon saat photon dipancarkan dari
permukaan bintang sejauh 20 m ?
Penyelesaian menggunakan persamaan (22).
gs
f
f! f
Jika perubahan frekuensi relatif
=
= 2
c
f
f
Dengan nilai g = 9,8 ms-2 dan c = 3 .108 ms-1 maka nilai
f
= 2,2 .10-15.
f
56
Bila frekuensi photon bergerak menuju bumi bertambah (panjang gelombang menjadi panjang menuju merah) sehingga saat menjauhi bumi berkurang (disebut pergeseran merah grafitasi). Medan
M
gravitasi bumi tidak begitu kuat, tetapi me
f!
dan gravitasi bintang sangat kuat . Misal
hf
photon (massa m = 2 ) berfrekuensi awal
c
Gambar 8.
f dipancarkan oleh sebuah bintang bermassa M berjari-jari R sehingga energi potensial photon pada permukaan bintang
Mm
Ep = - G
23a
R
Persamaan (23a) tanda (-) menunjukkan tarik menarik dengan demikian persamaR
f
an (23a) menjadi
Mhf
Ep = - G 2
23b
c R
Energi total (E) jumlahan dari energi kuantum hf ialah
Mhf
M
E = hf - G 2 = hf (1 – G 2 )
24
c R
c R
Pada jarak yang cukup jauh dari bintang (misal di bumi) photon tersebut di luar
jangkauan medan gravitasi bintang (energi totalnya tetap). Dengan demikian photon energinya keseluruhan dalam bentuk elektromagnetik dan E = hf !, (f menyatakan frekuensi elektron datang). Karena Ep photon dalam medan gravitasi bumi
diabaikan dibandingkan dengan medan gravitasi bintang sehingga persamaan (24)
M
M
f!
menjadi hf! = hf (1 - G 2 ) atau
= 1-G 2
akhirnya
c R
c R
f
M
f
f
f! f
=
= 1= G 2
25
c R
f
f
f
Photon berfrekuensi rendah di bumi bersesuaian dengan kehilangan energinya ketika photon tersebut meninggalkan bintang (terjadi pergeseran spektrum).
M
Bila terjadi G 2 ≥ 1 persamaan (25) tidak akan ada photon yang ke luar
c R
dari bintang. Bintang sejenis ini tidak dapat memancarkan photon [tidak tampak
suatu lubang hitam (black hole)].
Contoh 11.
Carilah (pendekatan) pergeseran merah gravitasi pada cahaya 5000 Ao yang
dipancarkan oleh bintang kerdil putih yang massanya sama dengan massa mataha-
57
ri [jari-jari sama dengan jari-jari bumi (6,4 .106 m)] !
Penyelesaian menggunakan persamaan (25)
M
f
c
3 .108 ms 1
= G 2
dan f =
=
= 6 .1014 Hz
7

5 .10 m
c R
f
Dari soal diketahui tetapan-tetapan dengan nilai λ = 5000 Ao = 5 .10-7 m
M = 2 .1030 kg ; R = 6,4 .106 m ; c = 3 .108 m s-1 dan G = 6,67 .10-11 m3 kg-1 s-2
M
c
Dari nilai-nilai tersebut dihasilkan ∆f =
G 2 diperoleh ∆f = 1,40 .1011 Hz.

c R
11
f

1,4 .10 Hz
Dengan demikian
=
=
≈ 2,3 .10-4
14

6 .10 Hz
f