e t RC Q q dt RC q dq q RC dt dq

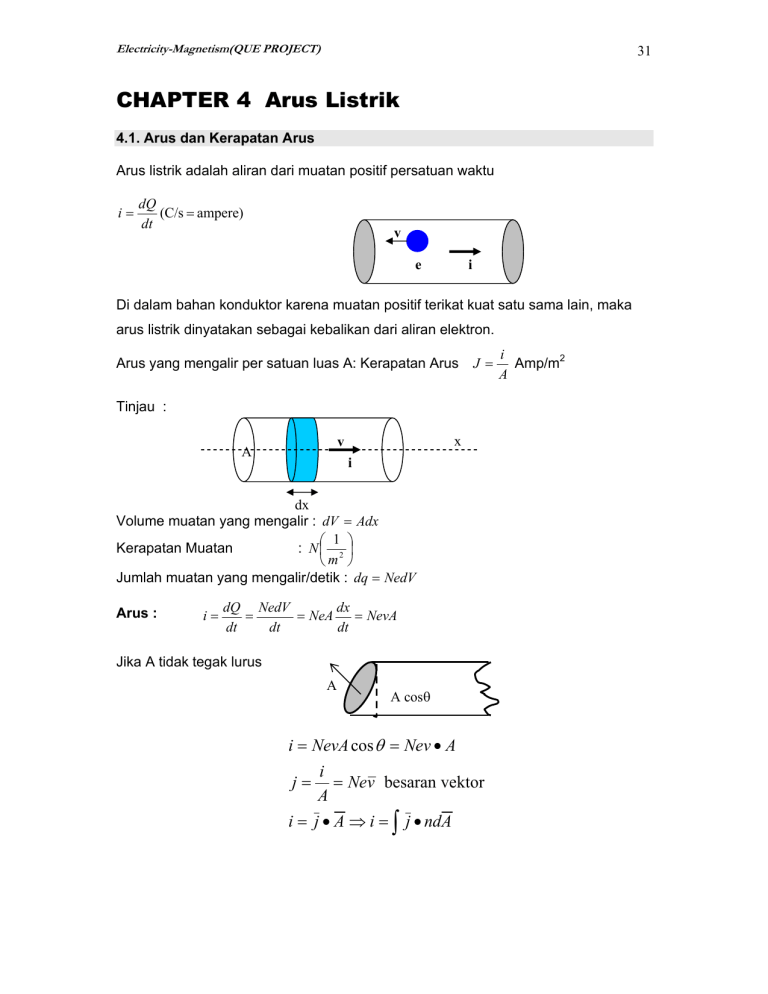
Electricity-Magnetism(QUE PROJECT)
31
CHAPTER 4 Arus Listrik
4.1. Arus dan Kerapatan Arus
Arus listrik adalah aliran dari muatan positif persatuan waktu
i=
dQ
(C/s = ampere)
dt
v
e
i
Di dalam bahan konduktor karena muatan positif terikat kuat satu sama lain, maka
arus listrik dinyatakan sebagai kebalikan dari aliran elektron.
Arus yang mengalir per satuan luas A: Kerapatan Arus
J=
Tinjau :
x
v
A
i
dx
Volume muatan yang mengalir : dV = Adx
⎛ 1 ⎞
Kerapatan Muatan
: N⎜ 2 ⎟
⎝m ⎠
Jumlah muatan yang mengalir/detik : dq = NedV
Arus :
i=
dQ NedV
dx
=
= NeA
= NevA
dt
dt
dt
Jika A tidak tegak lurus
A
A cosθ
i = NevA cos θ = Nev • A
j=
i
= Nev besaran vektor
A
i = j • A ⇒ i = ∫ j • ndA
i
Amp/m2
A
Electricity-Magnetism(QUE PROJECT)
32
4.2. Hambatan dan Hukum Ohm
Hambatan listrik : halangan gerak muatan ketika mengalir
•
tabrakan sesama muatan
•
tabrakan dengan muatan dari atom , zat lain, dll.
Bahan Konduktor : banyak elektron bebas : ⇒ Selalu bergerak acak dengan
kecepatan vi.
⇒
∑v
i
= 0 ⇒ i = NevA = 0
i
∑viτi
⇒ vdrift = t
∑
vdrift <<vi
i
⇒ menghasilkan
arus
Bila diberi medan listrik E : 1. bergerak menuju satu arah
2.
∑v
i
≠0
3. i = NevA ≠ 0
4. akan terjadi tabrakan→hambatan
me = massa e
l = jarak bebas rata-rata
τ = waktu relaksasi
v` = kecepatan sebelum tumbukan
v`` = kecepatan sesudah tumbukan
Bila tumbukan elastis :
v`=v``=v
Δ (mv) = me v`− me v``= me v + me v = 2me v
Δ (mv) = F • Δτ
Hukum Kekekalan Impuls=momentum : Δ (mv) = FΔτ ; Δt = 2τ
2me v = 2eEτ
eτ
v=
E
me
I≺E
; i = NevA
I ≺v
mev`
l
Electricity-Magnetism(QUE PROJECT)
33
J=
i
e 2τ
=N
E
A
me
e 2τ
= konduktansi ( kemampuan hantar muatan bahan)
me
1
m
J = gE
;
g=
;
ρ=
;
ρ
Ne 2τ
g=
i=
since V pot = E • L
thus
:
Ne 2τ V
i=
A
me L
i=
Conductor
Ne 2τ
AE
me
V pot
R
;
1A 1
=
ρL R
⇒ V = iR
N≈1027/m3
:
Tergantung temperatur : bila temperatur dinaikkan L dan τ
mengecil, ρ membesar
Nonconductor :
N≈0
g=0, ρ→∞
Semiconductor:
g antara conductor dan nonconductor.
T rendah, sifatnya sama seperti nonconductor.
T mendekati temperatur ruang, hambatan turun bila bahan
dipanaskan.
Resistor dan rangkaiannya
a. Seri
i
V1
V2
R1
R2
i = konstan disetiap cabang
v=v1+v2+…..+vn
R=Σ Ri
V = iR = i ( R1 + R2 + ...... Rn )
Electricity-Magnetism(QUE PROJECT)
34
b. Paralel
V di setiap titik cabang konstan
i=i1+i2+i3+…..+in
1
1
1
i = v( +
+ ...... + )
R1 R2
Rn
i
i1
R1
i2
R2
in
Rn
n
1
1
=∑
R i =1 Rn
i
Potensiometer :
Pembagi potensial
Pengukur potensial
Rheostat (hambatan variabel)
Pembagi potensial
i
Vin
R1
R2
V in = i ( R 1 + R 2 )
V out = iR
2
V in =
V out
( R1 + R 2 )
R2
V out =
R2
V in
R1 + R 2
Vout
Electricity-Magnetism(QUE PROJECT)
35
Pengukur potensial
Galvanometer
E
R
εx
Bila arus pada galvanometer = 0
Ex =
Where εx replace by εs and R by Rs
Rheostat
Rx
E s tan dar
Rs
:
Contoh lain :
εx
r
G
i
I
i0
II
R
( i0 - i )
R0
In loop I
:
− ε x − ir + (i0 − i) R = 0
i=
i0 R − ε x
R+r
E0
Electricity-Magnetism(QUE PROJECT)
36
Replace εx by a standard emf εs and then adjust again R to the zero circuit condition.
R = variable resistor
i0 R x = ε x , i=0
If R is adjusted to have the value Rx where,
i0 R s = ε s
εx = εs
Rx
Rs
4.3. Daya Disipasi dan GGL
Daya Disipasi :
Besar energi listrik per satuan waktu melalui hambatan yang
berubah menjadi energi dalam bentuk panas.
dq
ε
W = ∫ Vdq ,
daya :
V
dW
= Vi ( watt )
dε
P = i2R
P=
Daya ini merupakan kerja persatuan waktu untuk melawan gerak muatan sehingga
menimbulkan panas.
Gaya Gerak Listrik (GGL), ε
: merupakan energi persatuan muatan untuk
menggerakkan muatan yang berasal dari sumber luar.
Sumber GGL :
Energi kimia
:
Energi matahari :
Energi Panas bumi.
1. elemen listrik (battery)
2. bahan bakar fosil
1. panas dan cahaya
2. energi gravitasi
3. ombak dan angin
Electricity-Magnetism(QUE PROJECT)
37
W = ∫ εdq
ε=
`
dw `
( watt )
dq
Beda potensial dan ggl : Potensial → statis
Ggl
→ dinamis
Di dalam sumber listrik pada saat muatan digerakkan, akan timbul hambatan Rd
setelah akan mencapai keadaan setimbang, arus yang mengalir I baik pada beban R
maupun Rd tetap.
a
dq
Rd
V
ε
b
εu = (R + Rd )i
Vad = ε − iRd
Bila Rd ⇒ ∞ , seluruh gerak muatan dihambat, i = 0, ε = 0
Contoh
:
10Ω
5.0Ω
8.7Ω
0.5Ω
9V
A 9.0 V battery whose internal resistance r=0.5Ω is connected as the figure. H ow
much current is drawn from the battery? What is the therminal voltage of battery ?
Electricity-Magnetism(QUE PROJECT)
RT = (
I=
38
10 × 8.7
R1 R2
)+5= (
) + 5 = 10.3Ω
18.7
R1 + R2
ε
RT
=
9
= 0.87 Amp
10 .3
Va = ε − ir = 9 − (0.87 )(0.5) = 8.6V
4.4. Hukum Kirchoff
I.
∑ε − ∑i R
i
j
j
=0
i
II.
∑i
j
Contoh
=0
:
R2
1.
i2
i3
R1
i4
i1
R3
I
:
ε − i1 R1 − i2 R2 − i1 (
II
:
i1
-
i3
i1
=
i2
R3 R4
)=0
R3 + R4
-
R2
i2
2. Jembatan Wheatstone
R4
i4
=
0
R3
i3
b
c
R5
i5
a
R6
i
R1
i1
d
ε
R4
i4
Electricity-Magnetism(QUE PROJECT)
39
A ⇒ ε − i1 R 1 − i1 R 4 − iR
6
= 0
B ⇒ i 2 R 2 + i 5 R 5 − i1 R 1 = 0
C ⇒ i5 R 5 + i 4 R 4 − i3 R 3 = 0
a ⇒ i − i1 − i 2 = 0
b ⇒ i2 − i3 − i5 = 0
c ⇒ i3 + i4 − i = 0
d ⇒ i1 + i 5 − i 4 = 0
R5 is variable, where i5=0
Thus,
R1
R2
=
R4
R3
4.5. Nonohmik Konduktor
ƒ
Conducting material that obey Ohm`s Law ( Δv = Ri or j = σε ) are designated
as Ohmik or linear conductors, because of the direct proposionality between the
voltage and current.
→most solid(mainly metal) or many liquids.
ƒ
Gase on conduction departs markedly from Ohm`s Law, primarly because
conduction in gases is due not to the presence of free electrons bbut to the
production of ionized atoms or molecules, ( by passing high frequency EM
radiation : X-rays,γ-rays, or by uncreasing the
temperature of
the gases
to ≈ 1000K).
ƒ
Metals depart from Ohm`s Law at very low temperature, because when
temperature is very low, the energy of the conduction electrons and of the lattice
ions is extremely small. The motion of the electrons is less hundred bby lattice
vibrations and conductivity increases appreciably.
Electricity-Magnetism(QUE PROJECT)
ƒ
40
In some substance, superconductors, the conductivity effectively becomes
infinite near absolute zero.
ƒ
There are some conducting solids that do not obey Ohm`s Law even at room
temperature⇒non-ohmic conductors
: ceramic, semiconductor,p-n junctions,
boundary layers between metals and their oxide.
Iron alloy filament in hidrogen atmosphere.
I(A)
Carbon
Tungsten
Lamp filament characteristic
ΔV (Volt)
I (A)
ΔV (V)
Asymmetric system CaCuO ( current not only depend on magnitude of
applied voltage but also on the direction invalid the voltage is applied)
Metallic copper caused with a layer of copper oxide
Electricity-Magnetism(QUE PROJECT)
41
4.6. RC-Circuits
Time varying currents
a
R
s
b
C
ε
i=
dq
⇒ dq = idt
dt
if S on at a :
the work done by emf must equal the energy that appear as the thermal energy in R
during time dt ( i2R dt ) plus the increase in the amount of energy U that is stored in
⎛ q2 ⎞
⎟⎟ ).
the capacitor ( dU = d ⎜⎜
⎝ 2C ⎠
ε dq = i 2 Rdt
+ d (
ε dq = i 2 Rdt
+
q2
)
2C
q
dq
C
Dividing by dε :
ε
dq
q dq
= i2R +
dε
C dε
ε = iR +
q
C
Electricity-Magnetism(QUE PROJECT)
From loop
:
Differential equation
:
⇒ Solution
at
ε
R
q
= 0
C
ε − iR −
ε = R
dq
q
+
dt
C
q = C ε (1 − e
:
E=0, q=0 , i =
42
dq
dt
,
= i =
ε
R
e
t
RC
−
)
t
−
RC
t ⇒ ∞ , q ⇒ Cε , i=0
q
Cε
Vc
Va
i
ε
R
t
RC = Capacity time constant, the charge on the capacitor has increased to a factor
( (1 − e −1 ) and q = 0.63 Cε.
If S is in b after the capacitor is fully charged
:
Electricity-Magnetism(QUE PROJECT)
43
iR
+
R
dq
dt
q
C
= 0
q
C
+
q = q 0e
i = −
⇒
ε
R
−
e
= 0
t
RC
−
t
RC
, q0=Cε
1
dq
=
q
dt
RC
q
∫
Q0
1
dq
= −
q
RC
t
∫ dt
0
q
1
ln
= −
t
Q0
RC
⇒
q = Q 0e
−
t
RC