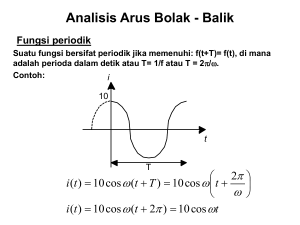
RANGKAIAN LISTRIK

RANGKAIAN LISTRIK
Kuliah 4 ( Analisa Arus Cabang dan Simpul DC )
ANALISA ARUS CABANG DAN SIMPUL DC

Metoda analisis rangkaian sebenarnya merupakan salah
satu alat bantu untuk menyelesaikan suatu permasalahan
yang muncul dalam menganalisis suatu rangkaian, bilamana
konsep dasar atau hukum-hukum dasar seperti Hukum
Ohm dan Hukum Kirchoff tidak dapat menyelesaikan
permasalahan pada rangkaian tersebut.

Pada bab ini akan dibahas tiga metoda analisis rangkaian
yang akan dipakai, yaitu : analisis node dan analisis mesh
dan analisis arus cabang.
ANALISIS NODE (1)

Analisis node berprinsip pada Hukum Kirchoff I (KCL=Kirchoff
Current Law atau Hukum Arus Kirchoff = HAK ), dimana :
jumlah arus yang masuk dan keluar dari suatu titik percabangan
akan sama dengan nol, dan tegangan merupakan parameter yang
tidak diketahui.
Atau analisis node lebih mudah jika pencatunya semuanya adalah
sumber arus.
ANALISIS NODE (2)
Beberapa hal yang perlu diperhatikan pada analisis node, yaitu :
 Tentukan node referensi sebagai ground (potensial nol).
 Tentukan node voltage, yaitu tegangan antara node non referensi
dan ground.
 Asumsikan tegangan node yang sedang diperhitungkan lebih
tinggi daripada tegangan node manapun, sehingga arah arus
keluar dari node tersebut positif.
 Jika terdapat N node, maka jumlah node voltage adalah (N-1).
Jumlah node voltage ini sama dengan banyaknya persamaan yang
dihasilkan (N-1).
 Analisis node mudah dilakukan bila pencatunya berupa sumber
arus. Apabila pada rangkaian tersebut terdapat sumber tegangan,
maka sumber tegangan tersebut diperlakukan sebagai supernode,
yaitu menganggap sumber tegangan tersebut sebagai satu node.
ANALISIS NODE (3)

Node = setiap titik disepanjang kawat yang sama
Contoh
6K
V
10V
4K
3 node
ANALISIS NODE (4)

Berapa banyak node ada di dalam rangkaian di bawah
ini ?
MENENTUKAN PERSAMAAN

arus yang masuk node = arus yang meninggalkan node
0


Pada node 1 :
v1
v1  v2

 3.1
2
5
Pada node 2 :
v2
v v
 2 1  - (-1.4)
1
5
CONTOH
4Ω
-3A
3Ω
V1
V2
1Ω
-8A
2Ω
V3
5Ω
0V

Berapa banyak node atau persamaan ?
-25A
4Ω
-3A
3Ω
V1
V2
1Ω
-8A
2Ω
V3
5Ω
-25A
0V
Node 1
Persamaan 1
V1  V 3
V1  V 2
3
0
4
3
96  3V 1  3V 3  36  4V 1  4V 2  0
8
7V 1  4V 2  3V 3  132
4Ω
-3A
3Ω
V1
V2
1Ω
-8A
2Ω
V3
5Ω
-25A
0V
Node 2
Persamaan 2
V 2  V1
V 2 V 3 V 2  0
3

0
3
2
1
2V 2  2V 1  18  3V 2  3V 3  6V 2  0
 2V 1  11V 2  3V 3  18
4Ω
-3A
3Ω
V1
V2
1Ω
-8A
2Ω
V3
5Ω
-25A
0V
Node 3
Persamaan 3
V 3  V 2 V 3  V1
V30

 25 
0
2
4
5
10V 3  10V 2  5V 3  5V 1  500  4V 3  0
 5V 1  10V 2  19V 3  500
3 Persamaan Keseluruhannya
7V 1  4V 2  3V 3  132
 2V 1  11V 2  3V 3  18
 5V 1  10V 2  19V 3  500
Aturan Cramer (Opsional)
7V 1  4V 2  3V 3  132
 2V 1  11V 2  3V 3  18
 5V 1  10V 2  19V 3  500
 132
18
500
V1 
7
2
5
4
11
 10
4
11
 10
3
3
19 780

 0.956
3
816
3
19
7V 1  4V 2  3V 3  132
 2V 1  11V 2  3V 3  18
 5V 1  10V 2  19V 3  500
7  132
 2 18
 5 500
V2
7
4
 2 11
 5  10
7
2
5
V3 
7
2
5
4
11
 10
4
11
 10
3
3
19 8628

 10.576
3
816
3
19
 132
18
500
26220

 32.132
3
816
3
19
ANALISIS MESH (LOOP) (1)


Arus loop adalah arus yang dimisalkan mengalir dalam suatu
loop (lintasan tertutup). Arus loop sebenarnya tidak dapat
diukur (arus permisalan).
Berbeda dengan analisis node, pada analisis ini berprinsip pada
Hukum Kirchoff II (KVL = Kirchoff Voltage Law atau Hukum
Tegangan Kirchoff = HTK), dimana :
jumlah tegangan pada satu lintasan tertutup sama dengan nol
atau arus merupakan parameter yang tidak diketahui.
ANALISIS MESH (LOOP) (2)
Hal-hal yang perlu diperhatikan :
 Buatlah pada setiap loop arus asumsi yang melingkari loop.
Pengambilan arus loop terserah kita yang terpenting masih
dalam satu lintasan tertutup. Arah arus dapat searah satu sama
lain ataupun berlawanan baik searah jarum jam maupun
berlawanan dengan arah jarum jam.
 Biasanya jumlah arus loop menunjukkan jumlah persamaan arus
yang terjadi.
 Metoda ini mudah jika sumber pencatunya adalah sumber
tegangan.
 Jumlah persamaan = Jumlah cabang – Jumlah junction + 1
 Apabila ada sumber arus, maka diperlakukan sebagai supermesh.
Pada supermesh, pemilihan lintasan menghindari sumber arus
karena pada sumber arus tidak diketahui besar tegangan
terminalnya.
CONTOH :
CONTOH :

Gunakan analisis Mesh untuk menentukan Vx
1Ω I2
7V
2Ω
+ Vx I1
3Ω
6V
I3
2Ω
1Ω
1Ω I2
7V
2Ω
 7  1( I1  I 2)  6  2( I1  I 3)  0
Persamaan 1
3I 1  I 2  2 I 3  1
+ Vx -
I1
3Ω
6V
I3
2Ω
1Ω
1( I 2  I1)  2 I 2  3( I 2  I 3)  0
 I1  6 I 2  3I 3  0 Persamaan 2
2( I 3  I1)  6  3( I 3  I 2)  I 3  0
 2 I1  3I 2  6 I 3  6 Persamaan 3
I1 = 3A, I2 = 2A, I3 = 3A
Vx = 3(I3-I2) = 3V
Bagaimana memilih antara analisis Node
dan Mesh ???

Pilihlah salah satu yang persamaan nya paling sedikit untuk
menyelesaikan masalah!!!
CONTOH :

Dari contoh-contoh sebelumnya, analisis Node
mempunyai beberapa persamaan
7V
1Ω
V1
7V
2Ω
+ Vx -
V2
3Ω
7A
1Ω
V3
2Ω
0V
Contoh :
Kebergantungan Sumber
Tentukan Vx
1Ω
15A
I1
I2
2Ω
+ Vx 3Ω
1/9 Vx
I3
2Ω
1Ω
I1  15
1Ω
15A
I1
I2
2Ω
1( I 2  I1)  2 I 2  3( I 2  I 3)  0
 I1  6 I 2  3I 3  0 Persamaan 2
+ Vx 3Ω
1/9 Vx
I3
Persamaan 1
1Ω
2Ω
I1=15A, I2=11A, I3=17A
Vx = 3(17-11) = 18V
1
I 3  I1  Vx
9
Vx  3( I 3  I 2)
Persamaan 3
Persamaan 4
Contoh soal :
j2
A
I1
3 0oA
I
+
V1 
-
j2

+
I2
+
-
1/2 V1 12 0oV
+
-
V1
-
(a)
Dari gambar diatas didapatkan :
I  I1  I 2

V1  4 I  4 I 1  I 2

I1  30o A
Persamaan arus mesh :
V1  0,5V1  j 2 I 2  0 
I1
 30 o
3
o
I2 



225
1 j
2  45o
2
(b)
+
-
1/2 V1
TEOREMA SUPERPOSISI

Pada teorema ini hanya berlaku untuk rangkaian yang
bersifat linier, dimana rangkaian linier adalah suatu
rangkaian dimana persamaan yang muncul akan memenuhi
jika y = kx,
dimana k = konstanta dan x = variabel.

Dalam setiap rangkaian linier dengan beberapa buah
sumber tegangan atau sumber arus dapat dihitung dengan
cara :
Menjumlah-aljabarkan tegangan atau arus yang disebabkan
tiap sumber independent atau bebas yang bekerja sendiri,
dengan semua sumber tegangan atau arus independent atau
bebas lainnya dan diganti dengan impedansi dalamnya.
ELEMEN LINEAR VS. RANGKAIAN
LINEAR



Elemen Linear : elemen pasif yang mempunyai
hubungan tegangan-arus linear :
v(t)=R*i(t)
Sumber bergantung Linear : sumber yang outputnya
proporsional hanya pada nilai pertama : v1 = 0.6i114v2
Rangkaian Linear : mengandung sumber yang bebas,
sumber bergantung linear , dan elemen linear
CONTOH :
1V
1V
1Ω
I total
1Ω
1Ω
I1
2V
2V
I1 = 1A
I2 = 2A
I total = 1+2 = 3A
I2
CONTOH :
1A
1A
1Ω
I total
1Ω
1Ω
I1
2V
2V
I1 = 1A
I2 = 0A
I total = 1+0 = 1A
I2
CONTOH :
Tentukan tegangan Vx
6Ω
42V
4Ω
3Ω
+
Vx
-
10V
6Ω
42V
4Ω
3Ω
+
Vx
-
(3 || 4)
(12 / 7)
Vx( 42V ) 
 42 
 42
6  (3 || 4)
6  (12 / 7)
 9.333V
6Ω
4Ω
3Ω
+
Vx
-
10V
(6 || 3)
2
Vx(10V )  
10  
10
(6 || 3)  4
24
 3.333V
6Ω
42V
4Ω
3Ω
+
Vx
-
Vx  Vx( 42V )  Vx(10V )
 9.333  3.333  6V
10V
CONTOH :
Gunakan superposisi untuk menentukan ix
CONTOH :
i x'' = 0.8 A
i x' = 0.2 A
i x = 1.0 A
SUPERPOSISI DAN
SUMBER YANG TIDAK BEBAS
satu yang tidak dapat menggunakan superposisi
terhadap sumber yang tidak bebas!!!
Contoh :
Hukum Tegangan Kirchoff:
 10  2i x'  1i x'  2i x'  0
i x'  2
Supermesh:
''
''
''
2i x  1(i x  3)  2i x
''
i x  0.6
0
i x  i x'  i x''
 2  (0.6)  1.4 A

Teorema Thevenin
Pada teorema ini berlaku bahwa :
Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri dari
satu buah sumber tegangan yang dihubung-serikan dengan sebuah
impedansi ekivelennya pada dua terminal yang diamati.

Teorema Norton
Pada teorema ini berlaku bahwa :
Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri dari
satu buah sumber arus yang dihubung-paralelkan dengan sebuah
impedansi ekivelennya pada dua terminal yang diamati.

Transformasi Sumber
Resistor yang paralel dengan sumber arus ditransformasi menjadi
sumber tegangan dihubung seri dengan resistor.