Analisis Arus Bolak

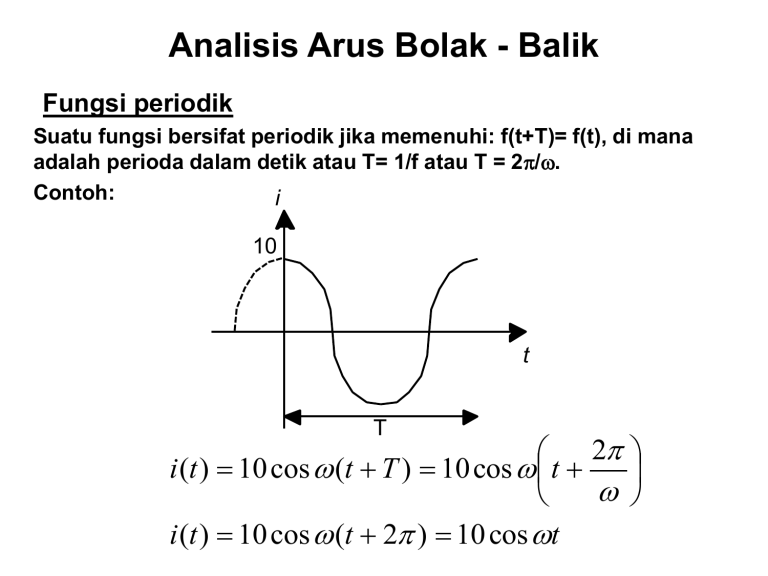
Analisis Arus Bolak - Balik
Fungsi periodik
Suatu fungsi bersifat periodik jika memenuhi: f(t+T)= f(t), di mana
adalah perioda dalam detik atau T= 1/f atau T = 2/.
Contoh:
i
10
t
T
 2 
i (t )  10 cos  (t  T )  10 cos   t 

 

i (t )  10 cos  (t  2 )  10 cos t
Nilai maksimum
Nilai maksimum ditulis sebagai Vmaks = Vm atau dalam arus Imaks =
Im. Dalam arus bolak balik terdapat dua nilai maksimum, yaitu
maksimum positif dan maksimum negatif. Bila dua nilai maksimum
tersebut dijumlahkan disebut sebagai nilai puncak-ke-puncak
(peak-to-peak).
Nilai efektif (root means square/rms)
Definisi: nilai tegangan/arus bolak-balik (ac) yang dapat
menghasilkan panas sama besar dengan panas yang dihasilkan
oleh tegangan/arus searah (dc). Secara matematis dapat
dinyatakan:
T
I eff  I rms
1 2

i t dt

T 0
Veff  Vrms
1 2

v t dt

T 0
T
Nilai sesaat
Nilai sesaat suatu tegangan atau arus adalah nilai tegangan atau
arus pada sebarang waktu peninjauan. Hal ini mengakibatkan
munculnya daya sesaat: p(t) = v(t) x i(t). Pengertian besaran dalam
persoalan pemindahan energi.
Nilai Rata-Rata
Nilai rata-rata suatu arus i(t) dalam satu perioda merupakan arus
konstan Iav, yang dalam perioda itu dapat memindahkan muatan Q
yang sama.
I av xT  Q 
T
I av
t T
T
t
0
 it dt   it dt
1
  i t dt
T 0
Dengan cara yang sama didapatkan :
T
1
Vav   vt dt
T0
Analisis Node
Analisis node berprinsip pada Hukum Kirchoff I/ KCL dimana
jumlah arus yang masuk dan keluar dari titik percabangan akan
samadengan nol, dimana tegangan merupakan parameter yang
tidak diketahui. Atau analisis node lebih mudah jika pencatunya
semuanya adalah sumber arus.
Beberapa hal yang perlu diperhatikan pada analisis node, yaitu :
Tentukan node referensi sebagai ground/ potensial nol.
Tentukan node voltage, yaitu tegangan antara node non
referensi dan ground.
Asumsikan tegangan node yang sedang diperhitungkan lebih
tinggi daripada tegangan node manapun, sehingga arah arus keluar
dari node tersebut positif.
Jika terdapat N node, maka jumlah node voltage adalah (N-1).
Jumlah node voltage ini akan menentukan banyaknya persamaan
yang dihasilkan.
Analisis node mudah dilakukan bila pencatunya berupa sumber
arus. Apabila pada rangkaian tersebut terdapat sumber tegangan,
maka sumber tegangan tersebut diperlakukan sebagai supernode,
yaitu menganggap sumber tegangan tersebut dianggap sebagai
satu node.
Contoh soal :
1/8 F
i
3 cos 4t A
+
v1
-

I
+
-
1/2 v1
3 0oA
+
V1 
-
(a)
(b)
Node A :
V1  0,5V1
I
 30 o
 j2
V1  4 I
Dengan mensubstitusikan didapat :
30
30
3
o
I


  45
o
1 j
245
2
o
j2
A
o
+
-
1/2 V1
Diubah ke kawasan waktu lagi :
i(t ) 
3
2

cos 4t  45 o

Analisis Mesh
Arus loop adalah arus yang dimisalkan mengalir dalam suatu loop
(lintasan tertutup). Arus loop sebenarnya tidak dapat diukur (arus
permisalan).
Berbeda dengan analisis node, pada analisis ini berprinsip pada
Hukum Kirchoff II/ KVL dimana jumlah tegangan pada satu lintasan
tertutup samadengan nol atau arus merupakan parameter yang tidak
diketahui.
Hal-hal yang perlu diperhatikan :
Buatlah pada setiap loop arus asumsi yang melingkari loop.
Pengambilan arus loop terserah kita yang terpenting masih dalam
satu lintasan tertutup. Arah arus dapat searah satu sama lain
ataupun berlawanan baik searah jarum jam maupun berlawanan
dengan arah jarum jam.
Biasanya jumlah arus loop menunjukkan jumlah persamaan arus
yang terjadi.
Metoda ini mudah jika sumber pencatunya adalah sumber
tegangan.
Jumlah persamaan = Jumlah cabang – Jumlah junction + 1
Apabila ada sumber arus, maka diperlakukan sebagai supermesh.
Pada supermesh, pemilihan lintasan menghindari sumber arus
karena pada sumber arus tidak diketahui besar tegangan
terminalnya.
Contoh soal :
j2
A
I1
3 0oA
I
+
V1 
-
j2

+
I2
+
-
1/2 V1 12 0oV
+
-
V1
-
(a)
(b)
Dari gambar diatas didapatkan :
I  I1  I 2

V1  4 I  4 I 1  I 2

I1  30o A
Persamaan arus mesh :
V1  0,5V1  j 2 I 2  0 
I1
I2 

1 j
 30 o
2  45 o

3
2
225 o
+
-
1/2 V1
Teorema Superposisi
Pada teorema ini hanya berlaku untuk rangkaian yang bersifat linier,
dimana rangkaian linier adalah suatu rangkaian dimana persamaan
yang muncul akan memenuhi jika y = kx, dimana k = konstanta dan x
= variabel.
Dalam setiap rangkaian linier dengan beberapa buah sumber
tegangan/ sumber arus dapat dihitung dengan cara :
Menjumlah aljabarkan tegangan/ arus yang disebabkan tiap sumber
independent/ bebas yang bekerja sendiri, dengan semua sumber
tegangan/ arus independent/ bebas lainnya diganti dengan
impedansi dalamnya.
Teorema Thevenin
Pada teorema ini berlaku bahwa :
Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri
dari satu buah sumber tegangan yang dihubungserikan dengan
sebuah impedansi ekivelennya pada dua terminal yang diamati.
Teorema Norton
Pada teorema ini berlaku bahwa :
Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri
dari satu buah sumber arus yang dihubungparalelkan dengan
sebuah impedansi ekivelennya pada dua terminal yang diamati.
Transformasi Sumber
Resistor yang paralel dengan sumber arus ditransformasi menjadi
sumber tegangan dihubung seri dengan resistor.
Sumber Beda Frekuensi
Pada konsep fasor, parameter gelombang yang muncul hanya
amplituda dan fasa. Misal suatu rangkaian terdapat banyak sumber
dengan berfrekuensi berbeda-beda, maka analisis yang dapat
dilakukan adalah dengan superposisi. Jadi pada satu saat hanya
satu sumber hidup dan analisis rangkaian dapat menggunakan fasor
yang kemudian hasilnya dikonversi ke kawasan waktu. Hasil total
adalah penjumlahan dalam kawasan waktu dari kontribusi masingmasing sumber.
Contoh soal :
1/2 H
3
5 cos 2t V
+
-
1H
i
1/2 F
1/4 F
1
1H
Rangkaian dengan sumber beda frekuensi pada kawasan waktu.
Pada sumber ac, w = 2 rad/s, sedangkan sumber dc, w = 0. Dengan
demikian, analisis rangkaian dengan menggunakan superposisi. Jika
sumber ac 'hidup' dan sumber dc 'mati', maka rangkaian dalam fasor
menjadi seperti terlihat di gambar berikut :
3+j2 
j2 
I1
5/0O V
+
-
-j1 
1
(a)
I2
3
1
(b)
5/0O V
Arus adalah arus kontribusi sumber ac, yang besarnya adalah:
50 o
I1 
 2  8,1o
3  j 2  1  j 2 j1 / 1  j 2  j1
Diubah ke kawasan waktu :


i1  2 cos 2t  8,1o A
Selanjutnya, jika sumber dc 'hidup' dan sumber ac 'mati' seperti
terlihat di gambar diatas, maka:
 1 
o
I 2  
4  10 A
1 3 
Diubah ke kawasan waktu : i2 = - 1 A
Respon totalnya :


i  i1  i2  2 cos 2t  8,1o  1A