Proyeksi Vektor

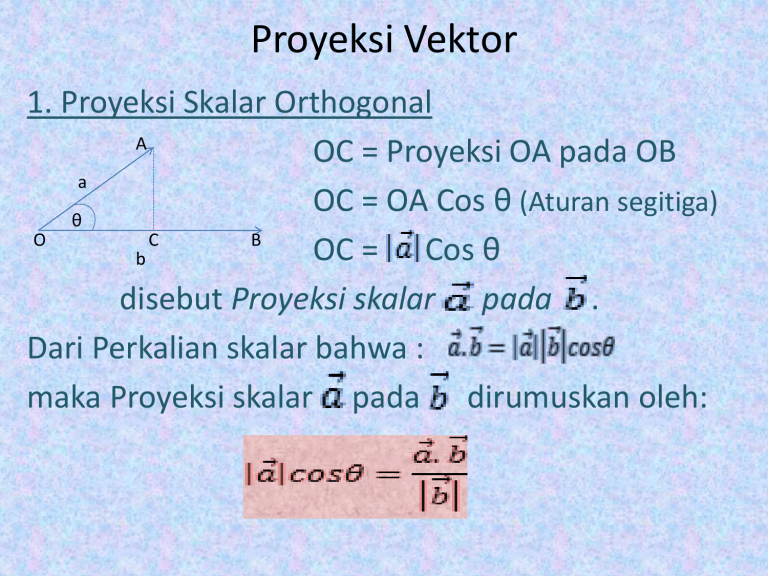
Proyeksi Vektor
1. Proyeksi Skalar Orthogonal
A
OC = Proyeksi OA pada OB
a
OC
=
OA
Cos
θ
(Aturan segitiga)
θ
O
C
B
OC = Cos θ
b
disebut Proyeksi skalar pada .
Dari Perkalian skalar bahwa :
maka Proyeksi skalar pada dirumuskan oleh:
2. Proyeksi Vektor Orthogonal
A
Dari Proyeksi skalar
pada
terdapat
=
yang disebut Proyeksi vektor ortogonal pada
yaitu suatu vektor yang segaris dengan .
O
θ
C
Sehingga Proyeksi vektor orthogonal
atau
B
pada
o
9
Panjang Proyeksi Vektor ortogonal
dapat dirumuskan sebagai :
pada
“ Bandingkan rumusan ini dengan rumusan
Proyeksi Skalar ortogonal pada “
Apa pendapatmu tentang hal tersebut ?
” MAMA ”
Beberapa Soal dan solusi
STOP PRESS..!!
Sesaat dibuang
sayang…!!
Contoh 1 :
Diketahui segitiga ABC, dengan
A(0,0,0), B(2,2,0) dan____
C(0,2,2). ____
Proyeksi orthogonal ABpada AC
adalah ….
Pembahasan
____
____
Proyeksi orthogonal AB pada AC =
____
AB= 2i + 2j
____
, AC= 2j + 2k
=
= ½(2j +2k)
= j+k
Contoh 2
Diketahui vektor - vektor :
a  3i  4 j  4k
b  2i  j  3k
c  4i  3 j  5k
Panjang proyeksi vektor (a  b )
pada c adalah ….
Pembahasan :
Pembahasan

Panjang proyeksi vektor (a  b ) pada c
  
(a  b). c

c
a  3i  4 j  4k ,
b  2i  j  3k
c  4i  3 j  5k
a  b  (3i  4 j  4k )  (2i  j  3k )
 5i  5 j  k
(a  b).c  (5)( 4)  (5)( 3)  (1)(5 )  30
c  4i  3 j  5k
c 
4  (3)  5 
2
2
2
50
(a  b).c  30
Sehingga Panjang Proyeksi vektor (a  b ) pada c
  
(a  b).c
30
30
6



3 2

c
50 5 2
2
” Kegagalan itu biasa
dan kekurangan itu wajar;
n
dan keengganan belajar dari
kegagalan masa lalu ”
12