PELABELAN-(a,k) PADA GRAF DNA

PELABELAN-(a,
k) PADA GRAF DNA
Inne, Denny Riama Silaban, Kiki Ariyanti Sugeng
Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Indonesia
SEQUENCING BY HYBRIDIZATION GRAF DNA
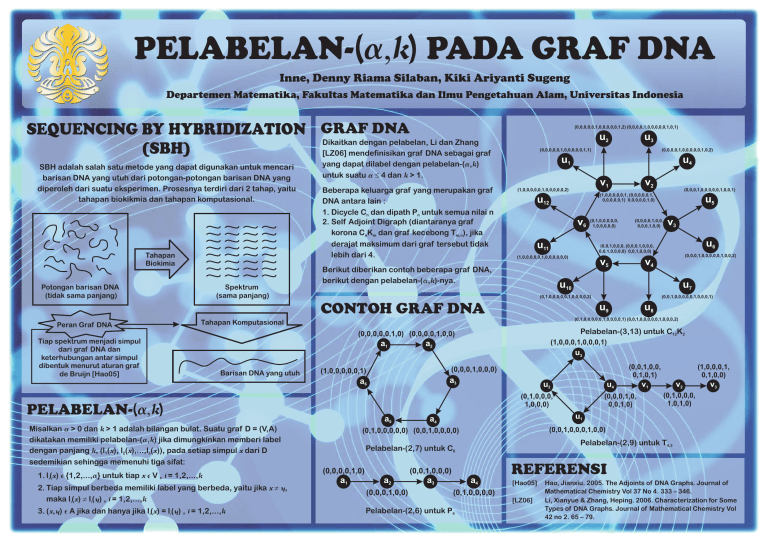
Dikaitkan dengan pelabelan, Li dan Zhang
(SBH)
[LZ06] mendefinisikan graf DNA sebagai graf
SBH adalah salah satu metode yang dapat digunakan untuk mencari
barisan DNA yang utuh dari potongan-potongan barisan DNA yang
diperoleh dari suatu eksperimen. Prosesnya terdiri dari 2 tahap, yaitu
tahapan biokikmia dan tahapan komputasional.
Beberapa keluarga graf yang merupakan graf
DNA antara lain :
1. Dicycle Cn dan dipath Pn untuk semua nilai n
2. Self Adjoint Digraph (diantaranya graf
korona CnKm dan graf kecebong Tm,n), jika
Potongan barisan DNA
(tidak sama panjang)
Spektrum
(sama panjang)
(0,0,0,0,0,1,0,0,0,0,0,1,1)
(0,0,0,0,1,0,0,0,0,0,1,0,2)
u1
u4
v1
(1,0,0,0,0,0,1,0,0,0,0,0,2)
u12
v6
(0,1,0,0,0,0,0,
1,0,0,0,0,0)
u11
(0,0,0,1,0,0,0,0,0,1,0,0,1)
u5
(0,0,0,0,1,0,0,
0,0,0,1,0,0)
v3
u6
(0,0,1,0,0,0, (0,0,0,1,0,0,0,
0,0,1,0,0,0,0) 0,0,1,0,0,0)
(1,0,0,0,0,0,1,0,0,0,0,0,0)
Berikut diberikan contoh beberapa graf DNA,
berikut dengan pelabelan-(a,k)-nya.
v5
(0,0,0,1,0,0,0,0,0,1,0,0,2)
v4
u10
u7
(0,1,0,0,0,0,0,1,0,0,0,0,2)
(0,0,1,0,0,0,0,0,1,0,0,0,1)
u9
u8
(0,1,0,0,0,0,0,1,0,0,0,0,1) (0,0,1,0,0,0,0,0,1,0,0,0,2)
Tahapan Komputasional
Pelabelan-(3,13) untuk C12K2
(0,0,0,0,0,1,0) (0,0,0,0,1,0,0)
Tiap spektrum menjadi simpul
dari graf DNA dan
keterhubungan antar simpul
dibentuk menurut aturan graf
de Bruijn [Hao05]
v2
(1,0,0,0,0,0,1, (0,0,0,0,0,1,
0,0,0,0,0,1) 0,0,0,0,0,1,0)
CONTOH GRAF DNA
Peran Graf DNA
u3
u2
yang dapat dilabel dengan pelabelan-(a,k)
untuk suatu a £
4 dan k > 1.
derajat maksimum dari graf tersebut tidak
lebih dari 4.
Tahapan
Biokimia
(0,0,0,0,0,1,0,0,0,0,0,1,2) (0,0,0,0,1,0,0,0,0,0,1,0,1)
a1
(1,0,0,0,1,0,0,0,1)
a2
u3
Barisan DNA yang utuh
a3
a6
u2
a5
Misalkan a > 0 dan k > 1 adalah bilangan bulat. Suatu graf D = (V,A)
dikatakan memiliki pelabelan-(a,k) jika dimungkinkan memberi label
dengan panjang k, (l1(x), l2(x),...,lk(x)), pada setiap simpul x dari D
3. (x,y) e A jika dan hanya jika li(x) = li(y) , i = 1,2,...,k
(0,0,1,0,0,0)
a2
(0,0,0,1,0,0)
v2
v3
(0,1,0,0,0,
1,0,1,0)
Pelabelan-(2,9) untuk T4,3
Pelabelan-(2,7) untuk C6
a1
v1
(0,0,1,0,0,0,1,0,0)
(0,1,0,0,0,0,0) (0,0,1,0,0,0,0)
(0,0,0,0,1,0)
(0,0,0,1,0,
0,0,1,0)
(1,0,0,0,1,
0,1,0,0)
u1
a4
sedemikian sehingga memenuhi tiga sifat:
2. Tiap simpul berbeda memiliki label yang berbeda, yaitu jika x ¹
y,
maka li(x) ¹
li(y) , i = 1,2,...,k
u4
(0,1,0,0,0,
1,0,0,0)
PELABELAN-(a,
k)
1. li(x) e {1,2,...,a} untuk tiap x e V , i = 1,2,...,k
(0,0,1,0,0,
0,1,0,1)
(0,0,0,1,0,0,0)
(1,0,0,0,0,0,1)
a3
a4
REFERENSI
[Hao05]
(0,1,0,0,0,0)
[LZ06]
Pelabelan-(2,6) untuk P4
Hao, Jianxiu. 2005. The Adjoints of DNA Graphs. Journal of
Mathematical Chemistry Vol 37 No 4. 333 – 346.
Li, Xianyue & Zhang, Heping. 2006. Characterization for Some
Types of DNA Graphs. Journal of Mathematical Chemistry Vol
42 no 2. 65 – 79.