Modul 8 Nilai Eigen

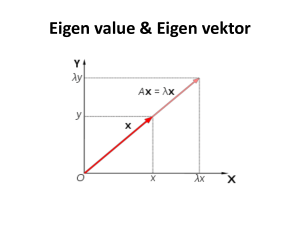
1
MODUL VIII
NILAI EGIEN DAN
VEKTOR EIGEN
Prayudi STT
PLN
Nilai Eigen dan Vektor Eigen
Andaikan A marik bujur sangkar berordo nxn, vektor taknol x di dalam Rn
dikatakan vektor eigen A, jika tedapat skalar taknol  sedemikian rupa
sehingga,
Ax = x
disebut dengan nilai eigen dari A dan x disebut vektor eigen dari A yang
bersesuaian dengan .
Contoh :
Vektor x = [1,2] adalah vektor eigen dari :
3 0 
A

8

1


yang bersesuaian dengan nilai eigen,  = 3, karena :
3 0  1 3
1
8  1 2  6  3 2

   
 
2
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Teknik Menghitung Nilai Eigen (1)
Untuk menghitung nilai eigen matrik A yang berorodo nxn tulislah Ax = x
sebagai,
Ax = Ix
(I – A)x = 0
  a11  a12
 a
21   a22

 a32
  a31

...
 ...
  an1
 an 2
 a13
...
 a23
...
 a 33
...
...
  aij
 an3
...
 a1n   x1   0 
 a2n   x 2   0 
   
 a3n   x3    0 
 
...   ...  ...
  ann   x n   0 
Agar supaya  menjadi nilai eigen, maka penyelesaian sistem
persamaan linier diatas haruslah non trivial, dimana syaratnya adalah :
det(I  A)  0
n  c1n 1  ...  cn 1  cn  0
3
Prayudi STT PLN
Teknik Menghitung Nilai Eigen (2)
Persamaan terakhir adalah polinomial  berderajad n yang
disebut dengan persamaan karakteritik A, sedangkan nilai
eigen matrik A adalah akar-akar persamaan karakteristik A
(akar-akar polinomial dalam ).
Langkah-langkah menentukan nilai eigen dan vektor eigen
matrik A adalah :
(1) Bentuk matrik (I – A)
(2) Hitung determinan, det(I – A)=0
(3) Tentukan persamaan karakteristik dari, (I – A) = 0
(4) Hitung akar-akar persamaan karakteristik (nilai lamda)
(5) Hitung vektor eigen dari SPL, (I – A)x=0
4
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Contoh
3 5 
Carilah nilai eigen dan vektor eigen dari, A = 

1  1
Jawab
Bentuk, I – A yaitu :
Untuk  = 4, diperoleh SPL


3

5


(I – A) = 
 1  5  x1  0

  1   1
 1 5   x   0

  2  
Persamaan karakteristiknya adalah :
Solusi SPL diatas adalah :
det(I – A) = 2 – 2 – 8 = 0
 x1  5t 
5
Akar-akar persamaan karakteristiknya
 x    t   t  1
 
 2  
adalah :  = 4, dan  = –2, dan inilah
1
2
nilai eigen matrik A.
Vektor eigen x dari A diperoleh dari :
(I – A)x = 0
  3  5   x1  0
  1   1  x   0

  2  
5
Jadi vektor eigen untuk  = 4,
adalah x = [5,1]. Sedangkan
vektor eigen yang bersesuaian
dengan  = –2 adalah, x = [1,–1].
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
  1 4  2
Contoh


Carilah nilai eigen dan vektor eigen dari, A =  3 4 0 
 3 1 3 
Jawab
Bentuk, I – A yaitu :
Untuk  = 1, diperoleh SPL
2 
  1  4

2  4 2   x1  0
4
0 
(I – A) =  3

3  3 0   x   0
 1   3
 3

  2  
3  1  2  x 3  0
Persamaan karakteristiknya adalah :
Solusi SPL diatas adalah :
det(I – A) = 3 – 62 + 11 – 6 = 0
 x1  t 
1
Akar-akar persamaan karakteristiknya
 x   t   t 1
adalah : 1 = 1, 2 = 2, dan 3 = 3
 2  

 x 3  t 
1
Vektor eigen x dari A diperoleh dari :
(I – A)x = 0
2   x1  0
  1  4
 3
4
0   x 2   0

    
 1   3  x 3  0
 3
6
Jadi vektor eigen yang
bersesuaian dengan :
 = 1 adalah x = [1,1,1] ;
 = 2 adalah x = [2,3,3] ;
 = 3 adalah x = [1,3,4].
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Diagonalisasi
Matrik bujur sangkar A dikatakan dapat didiagonalisasi jika terdapat matrik P
yang mempunyai invers sedemikian rupa sehingga, P–1AP adalah matrik
diagonal. Matrik P dikatakan mendiagonalisasi A.
Langkah-langkah menentukan matrik P dan D adalah sebagai berikut :
(1). Hitung persamaan karakteristik A nilai eigen
(2). Carilah n vektor eigen bebas linier A sesuai nilai eigen, p1,p2, ... , pn,
(3). Bantuklah matrik P = [p1 p2 … pn] dan hitunglah P–1
(4). Hitung, D = P–1AP dengan diagonal utama, 1, 2, … ,n
  1 4  2
1 2 1
3
Contoh :
A   3 4 0  P  1 3 3  P 1   1





 3 1 3 
1 3 4
 0
Vektor eigen dan nilai eigennya :
1 0
 = 1 adalah x = [1,1,1] ;

D = P–1AP = 0 2
 = 2 adalah x = [2,3,3] ;
 = 3 adalah x = [1,3,4].
0 0
7
Modul VIII Nilai dan Vektor Eigen
5
3 
3  2

 1 1 
0
0

3
Prayudi STT PLN
Contoh
2  2  2
Carilah nilai eigen, vektor eigen dan matrik
P yang mendiagonalisasi matrik A, bilamana A   1 5
2


5 
 1 2
Jawab
Menentukan nilai eigen A dan vektor eigen. Persamaan karakteristik A
diperoleh dari :
 2
2
2
det(I – A) = 0
1
 5
1
2
2 0
 5
Persamaan karakteristiknya adalah : 3 – 122 + 45 – 54 = 0. dan akarakarnya adalah : 1 = 2 = 3, dan 3 = 6. Vektor eigen x dari A diperoleh dari
: (I – A)x = 0
Untuk  = 3, SPL-nya
Solusi SPL-nya adalah :
Vektor eigen
2
2   x1  0
1
 x1 
  2
  2
p1 = [–2 ,1,0]
 1  2  2  x   0
x   t  1   s  0 

  2  
 2
 
 
p2 = [–2 ,0,1]
 1  2  2  x 3  0
 x 3 
 0 
 1 
8
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Untuk  = 6, SPL-nya
2
2   x1  0
4
 1 1  2  x   0

  2  
 1  2 1   x 3  0
Solusi SPL-nya adalah :
 x1   t 
 1
x    t   t  1 
 2  
 
 x 3   t 
 1 
Vektor eigen
p3 = [–1,1,1]
Matrik P yang mendiagonalisasi A adalah :
 2  2  1
1/ 3  2 / 3 
 1/ 3
1 

P = [p1 p2 p3] =  1
0
1
P


1
/
3

2
/
3
1
/
3




1
1 
 0
2/3
2 / 3 
 1/ 3
Matrik diagonal
1/ 3  2 / 3 2  2  2  2  2  1
 1/ 3

 
2 1
0
1
D = P–1AP =  1/ 3  2 / 3 1/ 3   1 5


2/3
2 / 3   1 2
5   0
1
1 
 1/ 3
3 0 0 
 0 3 0 


0 0 6
9
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Diagonalisasi Ortogonal
Matrik bujur sangkar A dikatakan dapat didiagonalisasi secara ortogonal
jika terdapat matrik P yang ortogonal sedemikian rupa sehingga, P–1AP
(=PTAP) adalah matrik diagonal (elemen matrik D adlah nilai eigen matrik
A). Matrik P dikatakan mendiagonalisasi A secara ortogonal.
Jika A adalah matrik nxn, maka pernyataan berikut ekivalen yakni :
(1). A dapat didiagonalisasi secara ortogonal,
(2). A matrik simetris,
(3). A mempunyai himpunan ortonormal n vektor eigen.
Langkah-langkah menentukan matrik P adalah sebagai berikut :
(1). Carilah n vektor eigen A yang bebas linier, x1, x2, ... , xn.
(2). Terapkan proses Gram-Schmidt untuk membentuk basis ortonormal,
dari vektor basis pada langkah (1).
(3). Bentuk matrik P dari langkah (2), yakni P = [p1 p2 … pn]
10
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
Contoh
Carilah matrik P yang mendiagonalisasikan
matrik A, secara ortogonal bilamana
 2 1  2
A 1 2 2 


 2 2  1
Jawab
Menentukan nilai eigen dan vktor eigen A. Persamaan karakteristik A
diperoleh dari :
  2 1
2
det(I – A) = 0
1   2  2  0
2
 2  1
Persamaan karakteristiknya adalah : 3 – 32 – 9 + 27 = 0. dan akar-akar
atau nilai eigennya adalah : 1 = 2 = 3, dan 3 = –3.
Vektor eigen x dari A diperoleh dari : (I – A)x = 0
Untuk  = 3, SPL-nya
Solusi SPL-nya adalah :
 x1 
 1
  2
 1  1 2   x1  0
 x   t  1  s  0 
 1 1  2  x   0
 2
 
 

  2  
 x 3 
0
 1 
 2  2 4   x 3  0
11
Modul VIII Nilai dan Vektor Eigen
Vektor eigen
x1 = [1,1,0]
x2 = [–2 ,0,1]
Prayudi STT PLN
Untuk  = 6, SPL-nya
 5  1 2   x1  0
  1  5  2  x   0

  2  
 2  2  2  x 3  0
Solusi SPL-nya adalah :
 x1   t 
1
 x    t   t  1
 2  
 
 x 3   2t 
 2 
Menentukan P = [p1 p2 p3]
x1
[1,1,0]  1 1 

  , ,0
| x1 |
2
 2 2 
Menghitung p2
x3 = [1,–1,2]
v2 = x2 – [x2,p1]p1
= [–2,0,1] – [–1,–1,0] = [–1,1,1]
Menghitung p1
p1 
Vektor eigen
p2 
[ 1,1,1]  1 1 1 
 
, , 
3
 3 3 3
Menghitung p3
p2 = v2/|v2|, dengan v2 = x2 – [x2,p1]p1 p = v /|v |, dengan :
3
3
3
1
1
2


[x2,p1] = [ 2,0,1]   , ,0  
v3 = x3 – [x3,p1]p1 – [x3,p2]p2
2
 2 2 
 1 1 
2  1 1 
[
1
,

1
,
2
]

, ,0  0
[x3,p1] =


,
,
0

[

1
,

1
,
0
]
[x2,p1]p1 =
 2 2 
2  2 2 
12
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
[x3,p1]p1 = [0,0,0]
Sehingga, v3 = x3 = [1,–1,2]
1 1 1 
[x3,p2] = [1,1,2]  
 3 , 3 , 3   0
[x3,p2]p2 = [0,0,0]
p2 
[1,1,2]  1
1 2 
  ,
, 
6
6 6
 6
Dengan demikian,



P = [p1 p2 p3] = 



13
1
2
1
2
0

1
3
1
3
1
3
1 
6 
1 


6
2 
6 
 1
 2
 1
T
P  
 3
 1
 6
Modul VIII Nilai dan Vektor Eigen
1
2
1
3
1

6

0 
1 

3
2 
6 
Prayudi STT PLN
SOAL-SOAL LATIHAN
a. Tentukan persamaan karakteristik, nilai eigen matrik A
b. Tentukan vector eigen A yang membentuk yang sesuai
dengan nilai eigen A.
c. Carilah matrik P yang mendiagonalisasikan A, dengan
rumus P= [x1 x2 … xn], dan D=P–1AP.
d. Dengan proses Gram-Schimdt, tentukan matrik P
mendiagonalisasikan A secara ortonormal,
P= [p1 p2 … pn], D=PTAP.
a
a 
a  b  1


A
a
a  b 1
a

 a

a
a

b

1


 a  b a  1  a  1


A   a 1 a  b a 1 
 a 1 a 1 a  b 


4  3
 1
 2  2 1
A 4
0  4  A    2  1 2




  3  4 1 
2 2
 1
14
 3 2 1 
A    2 6  2 A 


 1  2 3 
Modul VIII Nilai dan Vektor Eigen
Prayudi STT PLN
 4 2 2
 2 3 0


 2 0 5