Efek Fotolistrik
advertisement

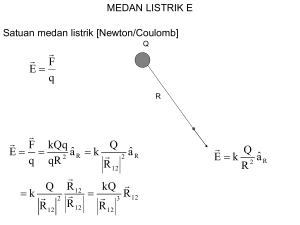
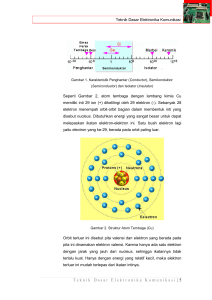
Efek Fotolistrik Einstein menjelaskan efek fotolistrik dengan hipotesis kuantum Albert Einstain 1879-1955 Efek Fotolistrik Emisi dari electron sebuah lempengan logam Efek Fotolistrik adalah fenomena quantum electronic dimana electrons di emisikan dari bahan setelah mengabsorp sejumlah energi dari radiasi elektromagnetik seperti x-rays atau visible light. Elektron yang diemisikan tersebut, pada tinjauan ini adalah photoelectrons. Efek ini juga dinamakan Hertz Effect, karena ditemukan oleh Heinrich Rudolf Hertz. Photoelectric effect Energi dari photon = Energi yang dibutuhkan untuk melepaskan sebuah electron + energi kinetik dari elektron yang dilepaskan hv 1 2 mv 2 1.4 Merupakam fungsi kerja dari logam, hampir mirip dengan energi ionisasi logam tersebut. Energi Kinetik tidak mungkin negatif, sehingga persamaan 1.4 dapat ditulis hv Frekuensi minimum yang dibutuhkan, yakni yang digunakan untuk mencapai fungsi kerja dari logam tersebut. Yang dikenal dengan “threshold frequency” (vo) hvo 1.5 Efek Fotolistrik Bagaimana menentukan nilai energi kinetik elektron ? • Jika elektron bergerak menuju elektrode bermuatan negatif, maka geraknya akan diperlambat karena melawan potensial listrik yang diberikan. Apabila potensial listrik terus ditingkatkan, maka elektron akan benar – benar “berhenti”. Nilai potensial yang dibutuhkan, disebut sebagai “stopping potential” • Pada “stopping potential” tersebut, energi kinetik dari elektron setara dengan potensial yang diberikan. 1 2 mv eVs 2 Dengan Vs adalah nilai “stopping potential” Efek Fotolistrik 1 2 hv mv 2 hvo 1 2 mv eVs 2 eVs hv hvo Persamaan diatas menunjukkan bahwa plot grafik dari Vs versus v akan memberikan sebuah garis lurus. Yang sesuai dengan hasil experimen dan nilai kemiringan (slope) adalah h/-e Efek Fotolistrik Bagaimana menyatakan fungsi kerja, dalam nilai electron volts (eV) ? Efek Fotolistrik Bagaimana menyatakan fungsi kerja, dalam nilai electron volts (eV) ? 1 ev adalah, energi ketika sebuah partikel dengan muatan sama seperti elektron (atau proton) melewati sebuah daerah dengan potensial sebesar 1volt (1 coulomb x 1 volt= 1 joule) 1eV = (1.602x10-19C)(1V) = 1.602x10-19J Contoh Soal: • Nilai fungsi kerja dari logam natrium adalah 1.82 ev,, berapakah ”threshold frequency (vo)” natrium ? Contoh Soal Nilai fungsi kerja dari logam natrium adalah 1.82 ev,, berapakah ”threshold frequency (vo)” natrium ? Penyelesaian : Mengubah nilai dari eV menjadi joule 1.602 x1019 J 1.82eV (1.82eV )( ) 2.92 x1019 J eV Dengan hvo 2.92 x1019 J 14 1 14 vo 4 . 40 x 10 s 4 . 40 x 10 Hz 34 6.626 x10 Js Contoh Soal • Logam Lithium di radiasi dengan cahaya, diketahui nilai “stopping potential” 1.83 V untuk =3000Å dan 0.80 V untuk =4000 Å. Dari data tersebut dan muatan elektron, tentukan (a) konstanta Planck, (b) potensial threshold, dan © fungsi kerja logam lithium Penyelesaian (a): eVs e(V1 V2 ) eVs hv hvo h(v vo ) hc( 1 1 1 2 ) e(1.83V 0.80V ) (2.49 x1014 Hz )h 1 h 1.03V 4.14 x10 15 JsC 14 e 2.49 x10 Hz h (4.14 x10 15 JsC 1 )(1.602 x10 19 C ) 6.63 x10 34 Js Penyelesaian (b): Menggunakan data saat = 3000Å hc (1.602 x10 C )(1.83V ) hvo 7 3.00 x10 m 14 vo 5.57 x10 Hz 19 Penyelesaian (c): hvo 3.69 x10 19 J 2.30eV Kesimpulan • Menggunakan nilai muatan dari elektron, Einstein memperoleh nilai dari konstanta planck, mirip dengan nilai yang didapatkan dari persamaan radiasi benda hitam • Dua eksperimen yang sangat berbeda (radiasi benda hitam, dan efek fotolistrik) menghasilkan konstanta kuantisasi (h) yang universal Permasalahan 1. Pada panjang gelombang berapa, sebuah benda hitam akan menghasilkan nilai energi yang maksimum, jika terjadi pada (a) T=300K? (b) T=3000K? dan (c) T=10,000 K? 2. Sirius, sebuah bintang yang paling panas. Diperkirakan mempunyai radiasi dengan max=2600. Tentukan temperatur permukaan bintang sirius tersebut. Permasalahan 3. Diberikan fungsi kerja dari Chromium adalah 4.40 eV. Hitunglah energi kinetik dari elektron yang diemisikan dari permukaan chromium saat diradiasi dengan ultraviolet dengan = 2000A! Berapakah nilai “stopping potential” untuk elektron tersebut? Permasalahan 4. Ketika permukaan perak diradiasi dengan sinar pada 230 nm, nilai “stopping potential” dari elektron tersebut adalah 0.80 V. Hitunglah fungsi kerja dan “threshold frequency” dari perak !