DISTRIBUSI NORMAL

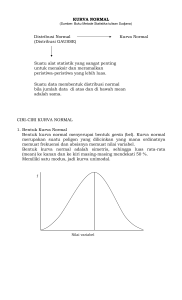
DISTRIBUSI NORMAL
 Distribusi normal sering disebut juga distribusi Gauss.
 Merupakan model distribusi probabilitas untuk variabel
acak kontinyu yang paling sering digunakan.
Sifat-sifat penting distribusi normal
1. Grafiknya selalu berada di atas sumbu X
2. Bentuknya simetrik terhadap X =
3. Mempunyai satu modus, jadi kurva unimodal (
mempunyai satu modus), tercapai pada X =
sebesar
4. Grafiknya mendekati sumbu datar X dimulai
dari X =
ke kanan dan X =
ke kiri
5. Luas daerah grafik selalu sama dengan satu unit
persegi.
Suatu distribusi dari sejumlah variabel dapat
dikatakan mendekati distribusi normal apabila:
1. Kira-kira 68% dari datanya terletak di dalam
interval
dan
.
2. Kira-kira 95% dari datanya terletak di dalam
interval
dan
.
3. Kira-kira 99% dari datanya terletak di dalam
interval
dan
.
 Jika X adalah sebuah variabel rambang normal, dengan
rata-rata populasi
dan simpangan baku
probabilitas fungsi massal dari X adalah :
, maka
 Untuk variabel yang berasal dari suatu distribusi
normal, nilai rata-rata harapan dan variannya adalah
sama dengan rata-rata populasi dan varian populasi.
 Dalam menghitung luas kurva (Z) untuk nilai-nilai
variabel X pada interval tertentu perlu diperhatikan
letak nilai-nilai X tersebut terhadap nilai rata-rata
populasinya
.
Dalam hal ini terdapat 8 kemungkinan.
Langkah-langkah dalam mencari bagian-bagian luas dari
distribusi normal baku :
1. Hitung Z sehingga 2 tempat desimal
2. Gambarkan kurvanya
3. Letakkan harga Z pada sumbu datar, lalu tarik garis vertikal
hingga memotong kurva
4. Luas yang tertera dalam daftar adalah luas daerah antara garis
ini dengan garis tegak titik nol
5. Dalam daftar F cari tempat harga Z pada kolom paling kiri
hanya hingga satu desimal dan desimal kedua dicari pada
baris paling atas
6. Dari Z di kolom kiri maju ke kanan dan dari Z di baris atas
turun ke bawah, maka di dapat bilangan yang merupakan luas
yang dicari. Bilangan yang didapat harus ditulis dalam bentuk
0,xxx ( 4 desimal).
Contoh Soal
1. Andaikan suatu populasi yang variabel-variabelnya
berdistribusi normal mempunyai nilai rata-rata
populasi = 0. Hitunglah probabilitas yang variabelvariabelnya terletak pada area :
a. Antara Z = 0 dan Z = 2
b. Antara Z = -1,28 dan Z = 0
c. Antara Z = -0,58 dan Z = 2,54
d. Antara Z = 1,20 dan Z = 2,44
e. Lebih besar dari Z = 2,87
2. Andaikan suatu populasi yang variabel-variabelnya
berdistribusi normal mempunyai nilai rata-rata
populasi
= 0. Hitunglah nilai Z untuk variabelvariabel acak yang mempunyai :
a. Probabilitas = 0,3413
b. Probabilitas = 0,8982
3. Berat bayi yang baru lahir rata-rata 3.750gram dan
simpangan baku 325 gram. Jika berat bayi berdistribusi
normal, maka tentukan :
a. Berapa persen bayi yang beratnya lebih dari 4.500gram
b.Berapa bayi yang beratnya antara 3.500gram dan
4.500gram, jika semuanya ada 10.000 bayi?
c. Berapa bayi yang beratnya lebih dari atau sama dengan
4.000gram jika semuanya ada 10.000 bayi?
d. Berapa bayi yang beratnya lebih dari 4.250 gram jika
semuanya ada 5.000 bayi?
TUGAS 4, DIKUMPULKAN
1. Suatu data yang populasinya berdistribusi normal
dimana = 0. Hitunglah probabilitas bagi variabelvariabel yang terletak pada area :
a. Antara Z = 0 dan Z = 2,25
b. Antara Z = 1,25 dan Z = 2,25
c. Antara Z = -2 dan Z = 1,44
d. Lebih dari Z = 2,53
2.Untuk suatu data yang populasinya berdistribusi
normal dimana
= 0 hitunglah nilai Z bagi variabelvariabel yang mempunyai :
a. Probabilitas (Z 0) = 0,4878
3.Tingkat kecerdasan mahasiswa baru sebuah
universitas yang distribusinya mendekati normal
adalah 110, sedangkan variannya 25. Adapun jumlah
seluruh mahasiswa baru 2600 orang.
a. Berapa probabilitas seorang mahasiswa baru yang
dipilih secara acak memiliki tingkat kecerdasan antara
110 dan 125 ?
b. Berapa persen yang memiliki tingkat kecerdasan
lebih dari atau sama dengan 120?
c. Berapa orang yang memiliki tingkat kecerdasan
antara 100 dan 115?