Nilai dan Vektor Eigen

Nilai dan Vektor Eigen
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Mengingat kembali: perkalian matriks
•
Diberikan matriks A2x2 dan vektor-vektor u, v, dan w
2 0
A

4 1
•
1 
v 
4
0
w 
 4
5
u 
 4
Hitunglah Au, Aw, Av. Manakah dari hasil kali tersebut yang hasilnya adalah vektor
yang sejajar dengan vektor semula
Jawab:
 2 0  1   2
1 
Av  


2
  4 8 
 4  2 v
4
1

    
 
2 0 0 0
Aw  
  4    4   1. w
4
1

    
 2 0 5  10 
Au  
    ku



 4 1   4  24
untuk semua k  R
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
v dan Av sejajar
w dan Aw sejajar
u dan Au TIDAK sejajar
Mengingat kembali: SPL homogen dan
determinan
1. A adalah matriks nxn dan SPL Ax = 0 mempunyai penyelesaian trivial saja.
Apa kesimpulanm tentang A?
Jawaban:
A mempunyai inverse. Det(A) ≠ 0
2. A adalah matriks nxn dan SPL Ax = 0 mempunyai penyelesaian TIDAK
trivial. Apa kesimpulanmu tentang A dan det(A)?
Jawaban:
A tidak mempunyai inverse.
Det(A) = 0
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
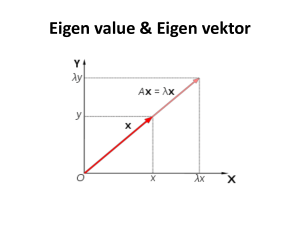
Perkalian vektor dengan matriks
A
x = λ x
Ax
x
x
Ax
x dan Ax sejajar
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Perkalian vektor dengan matriks
 2 0 1 
4 1  4

  
=2
1 
4
 
 2 0  0 
4 1  4

 
Au = 2u
 2 0  5 
4 1  4

  
0
=1  4 
 
y
10
24
2
8
0
4
1
4
x
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
k
5
4
 
Aw ≠ kw
Av = v
y
y
=
10 
 24 
 
5
4
x
x
Definisi: Nilai dan Vektor Eigen
Definisi:
Diberikan matriks A nxn, vektor tak nol v di Rn disebut vektor eigen
dari A jika terdapat skalar sedemikian hingga
Av = λv.
λ disebut nilai eigen, x adalah vektor eigen dari A yang
bersesuaian dengan λ .
Syarat perlu: v ≠ 0
(1) λ ≥ 1
(2) 0 ≤ λ ≤ 1
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
(3) -1 ≤ λ ≤ 0
(4) λ ≤ - 1
Masalah Vektor Eigen
Diberikan matriks persegi A,
A
x
A
x
sejajar
=
x
λ x
Temukan semua vektor tidak nol x sedemikian hingga Ax
adalah kelipatan skalar x (Ax sejajar dengan x).
atau
Temukan semua vektor tak nol x sedemikian hingga Ax = λx
untuk suatu skalar λ
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Masalah Nilai Eigen
Diberikan matriks persegi A.
A x
=
λ x
x vektor tak nol
Temukan semua skalar λ sedemikian hingga Ax = λx untuk suatu
vektor tak nol x.
atau
Temukan semua vektor skalar λ sedemikian hingga persamaan
Ax = λx mempunyai penyelesaian tak nol
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Pernyataan-pernyataan ekuivalen
Jika A matriks persegi nxn, maka kalimat-kalimat berikut ekuivalen
1.  nilai eigen A
2. terdapat vektor tak nol x sedemikian hingga Ax = x
3. SPL (A – I)x = 0 mempuyai solusi tidak nol (non-trivial)
4.  adalah penyelesaian persamaan det(A – I) = 0
Mencari nilai eigen A sama saja mencari penyelesaian
persamaan det(I-A) = 0
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Persamaan Karakteristik
Jika diuraikan, det((A - λI) merupakan suku banyak berderajat n dalam λ,
p(λ ) = λⁿ + cn-1λn-1 +cn-2 λn-2 + …+ c1λ+ c0 suku banyak karakteristik
Persamaan det((A - λI) = λⁿ + cn-1λn-1 +cn-2 λn-2 + …+ c1λ+ c0 = 0 disebut
persamaan karakteristik
A
det A-λI
-
λI
=
A-λI
•persamaan
karakteristik
= λⁿ + cn-1λn-1 +cn-2 λn-2 + …+ c1λ+ c0 = 0
Persamaan dengan derajat n mempunyai paling banyak n penyelesaian, jadi
matriks nxn paling banyak mempunyai n nilai eigen.
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Contoh
 2 0
Mencari semua nilai eigen A=  4 1 


Mencari semua penyelesaian persamaan det
2-λ
0
4
1-λ
=0
Mencari penyelesaian persamaan karakteristik (2 - λ )(1 - λ ) = 0
1  2,
Nilai eigen A adalah
2  1
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Prosedur: menentukan nilai eigen
Diberikan matriks persegi A.
Nilai-nilai eigen A dapat diperoleh sebagai berikut:
1. Tentukan persamaan karakteristik det((A - λI) = 0
tuliskan A dan matriks yang elemen diagonal utamanya dikurangi λ
2. (Jika diperlukan) uraikan persamaan karakteristik ke dalam persamaan
sukubanyak karakteristik:
λⁿ + cn-1λn-1 +cn-2 λn-2 + …+ c1λ+ c0 = 0
3. Selesaikan persamaan yang diperoleh pada langkah di atas. Nilai-nilai eigen
merupakan penyelesaian persamaan tersebut.
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Contoh: Menentukan nilai eigen
Diberikan matriks persegi
 1 1 1
A   0 3 3
 2 1 1
1. Tentukan persamaan karakteristik det(A - λI) = 0
1
1 
1  
det( A   I )  det  0
3
3 
 2
1
1   
(1   )2 (3   )  6  2(3   )  3(1   )  0
2. Ubahlah persamaan karakteristik ke dalam persamaan sukubanyak karakteristik:
3. Selesaikan persamaan di atas untuk memperoleh nilai-nilai eigen
(1   )2 (3   )  (3   )  0
 (  2)(3   )  0
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Nilai-nilai eigen A:
λ1 = 0
λ2 = 2
λ3 = 3
Nilai eigen matriks diagonal
Diberikan matriks diagonal
2
0
A
0

0
0 0 0
5 0 0 
0 6 0

0 0 1
0
2  
 0
5
A  I  
 0
0

0
 0
0 
0
0 
6
0 

0
1  
0
•Persamaan karakteristik: (2   )(5   )(6   )(1   )  0
•Nilai-nilai eigen 2, 6, 5, 1
(merupakan entri diagonal utama)
Nilai-nilai eigen matriks diagonal adalah elemen diagonal
utamanya.
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Bagaimana menentukan apakah suatu
skalar merupakan nilai eigen?
•
Tentukan apakah 2, 0, 4 merupakan nilai eigen A.
2 2 0
A   0 4 0
 0 1 0 
Jawab:
Bentuk det(A-λI) untuk λ = 2, 0, 4. Jika det(A-λI) ≠ 0, maka merupakan nilai eigen, kalau = 0,
maka bukan nilai eigen. Kunci: 2, 4 nilai eigen A, 0 bukan nilai eigen A.
2
0 
2  2

det( A  2 I )  det  0
42
0   0
 0
1
0  2
2
0 
2  0

det( A  0 I )  det  0
40
0   8  0
 0
1
0  0 
2
0 
2  4
det( A  4 I )  det  0
44
0   0
 0
1
0  4
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
2 adalah nilai eigen A
0 bukan nilai eigen A
4 nilai eigen A
Kelipatan skalar vektor eigen
•
Diberikan A. Diketahui bahwa x adalah vektor eigen A yang bersesuaian dengan nilai
eigen 2. Selidiki apakah 1/2x, 10x, 5x juga vektor-vektor eigen A
 1 1 1
A   0 3 3 ,
 2 1 1
 4
x   6
 2 
 2 
1 x   3
2
 
 1 
 1 1 1  4  8 
Ax   0 3 3  6   12  2 x
 2 1 1  2   4 
 40
10 x   60
 20 
 20 
5 x   30 
 10 
 1 1 1  40  80 
A(10 x)   0 3 3  60    120   2(10 x)
 2 1 1  20   40 
Ax = 2 x
A(10x) = 2 (10x)
λ
A
x =
A
(10) x =
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
x
λ
(10) x
Kelipatan skalar vektor eigen
 1 1 1
A   0 3 3 ,
 2 1 1
 2 
1 x   3
2
 
 1 
 4
x   6
 2 
 1 1 1  4  8 
Ax   0 3 3  6   12  2 x
 2 1 1  2   4 
 1 1 1  2
A( 12 x)   0 3 3  3 
 2 1 1  1 
Ax = 2 x
A
x =
 4
 6  2( 1 x)
2
 
 2 
A(1/2 x) = 2 (1/2 x)
λ
x
A
(1/2) x =
λ (1/2) x
Kelipatan skalar (tak nol) dari vektor eigen adalah
vektor eigen terhadap nilai eigen yang sama
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Menentukan semua vektor eigen Eλ
•
Diberikan vektor matriks A dan salah satu nilai eigennya, misalnya λ. Tentukan semua
vektor eigen yang bersesuaian dengan λ.
•
Vektor-vektor eigen A yang bersesuaian dengan λ = 3 dapat diperoleh dengan
menyelesaikan SPL (A - λ I)x = 0. Vektor eigen adalah anggota Null(A - λ I)
Null(A - λ I)
Himpunan semua penyelesaian
SPL (A - λ I)x = 0
Himpunan semua vektor eigen
bersesuaian dengan λ
0
Null(A - λ I)-{0}
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Ruang Eigen
Ruang eigen A yang bersesuaian dengan λ terdiri atas semua
vektor eigen yang bersesuaian dengan λ dan vektor nol
Ruang penyelesaian SPL (A - λ I)x = 0
Null(A - λ I)x
0
Ruang Eigen
Eλ
Null(A - λ I) = Eλ
Menentukan Eλ sama dengan menentukan himpunan penyelesaian SPL (A - λ I)x =
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
0
Menentukan ruang eigen Eλ
•
Diberikan vektor matriks A dan salah satu nilai eigennya, misalnya λ = 3. Tentukan
semua vektor eigen yang bersesuaian dengan λ = 3.
1
1 
1  3
A   I   0 3  3 3 
 2
1 1  3
 1 1 1
A   0 3 3
 2 1 1
SPL (A - 3 I)x = 0
1
1   x1  0
1  3
( A  3I ) x   0 3  3 3   x2   0
 2
1 1  3  x3  0
Penyelesaian x1

a
x2
 2a
x3

0
Himpunan penyelesaian
2 x1  x2  x3
 0
3x3
 0
2 x1  x2  2 x3
 0
 1 

  

a  2 , a  R 
 0

  

 1 


Himpunan vektor eigen A bersesuaian dengan λ =3 : a  2  , a  0, a  R 
 0

  

Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Nilai eigen matriks pangkat
•
•
Nilai eigen dari A adalah 0, 2, dan 3.
 1 1 1
A   0 3 3
 2 1 1
Tentukan nilai eigen untuk
 1 5 5 
A2   6 12 12 , A13 , A20
 4 2 1 
•
•
Diberikan sembarang matriks A dan diketahui bahwa λ adalah nilai eigennya.
Maka terdapat vektor tak nol x sedemikian hingga
Ax = λx
kalikan kedua ruas dengan matriks A
A.Ax = A λx
A2x = λ(Ax)
substitusi Ax dengan λx
A2x = λ2x
jadi, λ2 merupakan nilai eigen A2
Teorema: Jika n adalah bilangan bulat positif, λ nilai eigen matriks A, maka λn
adalah nilai eigen An
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Nilai eigen matriks singular
•
Misalkan  = 0 merupakan nilai eigen dari A.
Maka 0 merupakan penyelesaian persamaan karakteristik:
dengan menganti  dengan 0, diperoleh c0 = 0.
Padahal det(A- I) = 0, dengan = 0, maka det(A) = c0 = 0.
Karena det(A) = 0 maka A tidak mempunyai inverse.
•
Sebaliknya, det(A) = det(A - I) dengan mengambil  = 0.Jadi det(A) = c0.
Jika A tidak mempunyai inverse, maka det(A) = 0 = c0.
Sehingga  = 0 merupakan salah satu penyelesaian persamaan karakteristik;
 = 0 merupakan salah satu nilai eigen dari A.
0 adalah nilai eigen A jika dan hanya jika A
tidak mempunyai inverse.
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Nilai eigen matriks transpose
det(B) = det(BT)
(A-  I)T = (AT- I)
Misalkan  = 0 merupakan nilai eigen dari A,
 maka det(A-  I)= 0
Karena matriks dan transposenya mempunyai determinan yang sama,
 maka det(A-  I)T= 0
Karena (A-  I)T = (AT- I) ,
 maka det(AT-  I)= 0
Jadi,  adalah nilai eigen dari AT
A dan AT mempunyai nilai eigen yang sama
A dan A-1 mempuyai nilai
eigen yang sama
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Diagonalisasi
Definisi: Matriks persegi A dapat didiagonalkan jika terdapat matriks yang
mempunyai inverse sedemikian hingga P-1AP = D adalah matriks diagonal.
5 6

Contoh: A  

3 4 
 2 1
P

1
1


P-1AP=
 1 1
P 1  

 1 2 
 1 1 5 6   2 1
2 0 

D
 1 1
 1 2  





 3 4  
 0 1
Matriks
diagonal
A dapat didiagonalkan
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Kapan matriks A dapat didiagonalkan?
•
Teorema:
Jika A adalah matriks nxn, maka kalimat-kalimat berikut ini ekuivalen:
1. A dapat didiagonalkan
2. A mempunyai n vektor-vektor eigen yang bebas linier
Bukti (1)  (2)  a11

Diberikan A A   a21


 an1
a12
a22
an 2
a1n 
a2 n 


ann 
Misalkan A dapat didiagonalkan, maka terdapat matriks P yang mempunyai inverse
 p11
p
P   21


 pn1
p12
p22
pn 2
 p11
p
AP=PD   21


 pn1
p1n 
p2n 


pnn 
p1n 
p2n 


pnn 
p12
p22
pn 2
Sedemikian hingga P-1AP = D matriks diagonal
 1 p11 2 p12
 p
 1 21 2 p22


 1 pn1 2 pn 2
n p1n 
n p2n 


n pnn 
1 0
0 
2
D


0 0
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
0
0 


n 
Kapan matriks A dapat didiagonalkan?
(lanjt)
P-1AP = D, kalikan dengan P-1,
AP = PD
 p11
p
PD   21


 pn1
p12
p22
pn 2
 a11 a12
a
a
AP   21 22


 an1 an 2
p1n 
p2n 


pnn 
a1n 
a2n 


ann 
 1 0
0 
2



0 0
 p11
p
 21


 pn1
p12
p22
pn 2
0
0 


n 
 1 p11 2 p12
 p
2 p22
  1 21


 1 pn1 2 pn 2
p1n 
p2 n 


pnn 
  A p1
n p1n 
n p2n 


n pnn 
A p2
 1 p1 2 p2
n pn 
A pn 
AP = PD, jadi
Ap1  1 p1
Ap2  2 p2
Apn  n pn
Karena P mempunyai inverse, maka kolom-kolmnya bukan kolom nol.
Berdasarkan deinisi nilai eigen, maka λ1, λ2, λ3, …,λn merupakan nilai-nilai
eigen A, dan kolom-kolom P adalah vektor-vektor eigen A yang bebas linier
(karena P mempunya inverse)
Bukti untuk (2)  (1) kerjakanlah sebagai latihan untuk memperdalam
pemahaman.
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Prosedur mendiagonalkan matriks
•
Diberikan matriks Anxn. Akan dicari P sedemikian hingga PAP-1 = D.
Prosedur
1. Tentukan n vektor eigen A yang bebas linier, misalkan p1, p2, p3, …, pn
2. Dibentuk matriks P yang kolom-kolomnya adalah p1, p2, p3, …, pn
3. Mariks D = P-1AP adalah matriks diagonal yang entri diagonal utamanya
adalah λ1, λ2, λ3, …,λn dengan λj adalah nilai eigen bersesuaian dengan pj untuk
j = 1, 2, 3, …, n
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Contoh: mendiagonalkan matriks
•
Diberikan matriks Anxn. Akan dicari P sedemikian hingga PAP-1 = D.
5 6 
A

3 4 
Prosedur
1. Tentukan 2 vektor eigen A yang bebas linier. Pertama kita tentukan nilai-nilai eigennya
yaitu λ1= 2 dan λ2= -1 (telah dihitung sebelumnya). Tentukan vektor eigen bersesuaian
dengan nilai eigen, dengan menyelesaiakn SPL (A - λ I)x =0. Diperoleh
2
p1   
1 
1
p2   
1
2. Dibentuk matriks P yang kolom-kolomnya adalah vektor-vektor eigen di atas.
 2 1
P

 1 1
P
1
 1 1



1
2


3. Matriks D = P-1A P adalah matriks diagonal yang entri diagonal utamanya adalah λ1, λ2
berturut-turut
2 0 
D

0

1


Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia
Masalah Diagonalisasi dan masalah
vektor eigen
• Masalah vektor eigen
Diberikan matriks Anxn, apakah terdapat basis di Rn terdiri atas vektor-vektor
eigen?
• Masalah diagonalisasi
Diberikan matriks Anxn apakah terdapat matriks yang mempunyai inverse P
sedemikian hingga nP-1AP adalah matriks diagonal?
Teorema:
Anxn dapat didiagonalkan jika dan hanya jika terdapat n vektor eigen yang bebas
linier.
Padahal, setiap n vektor yang saling bebas linier di Rn merupakan basis Rn.
Kesimpulan: masalah vektor eigen sama dengan masalah diagonalisasi
Kuliah Jarak Jauh Program e-Learning Inherent
Fakultas Ilmu Komputer Universitas Indonesia