SAP Analisis Real B - Silabus Online IAIN Antasari Banjarmasin

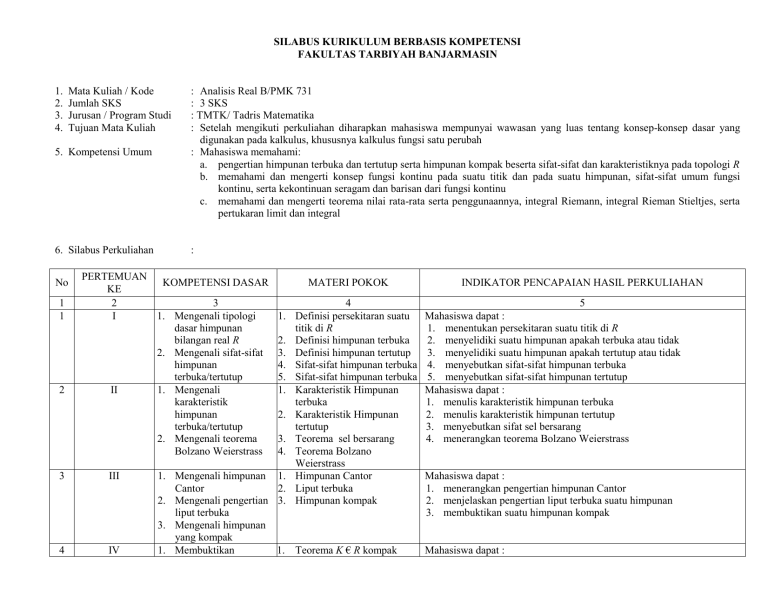
SILABUS KURIKULUM BERBASIS KOMPETENSI
FAKULTAS TARBIYAH BANJARMASIN
1.
2.
3.
4.
Mata Kuliah / Kode
Jumlah SKS
Jurusan / Program Studi
Tujuan Mata Kuliah
5. Kompetensi Umum
: Analisis Real B/PMK 731
: 3 SKS
: TMTK/ Tadris Matematika
: Setelah mengikuti perkuliahan diharapkan mahasiswa mempunyai wawasan yang luas tentang konsep-konsep dasar yang
digunakan pada kalkulus, khususnya kalkulus fungsi satu perubah
: Mahasiswa memahami:
a. pengertian himpunan terbuka dan tertutup serta himpunan kompak beserta sifat-sifat dan karakteristiknya pada topologi R
b. memahami dan mengerti konsep fungsi kontinu pada suatu titik dan pada suatu himpunan, sifat-sifat umum fungsi
kontinu, serta kekontinuan seragam dan barisan dari fungsi kontinu
c. memahami dan mengerti teorema nilai rata-rata serta penggunaannya, integral Riemann, integral Rieman Stieltjes, serta
pertukaran limit dan integral
6. Silabus Perkuliahan
:
No
1
1
2
3
PERTEMUAN
KOMPETENSI DASAR
KE
2
3
I
1. Mengenali tipologi
dasar himpunan
bilangan real R
2. Mengenali sifat-sifat
himpunan
terbuka/tertutup
II
1. Mengenali
karakteristik
himpunan
terbuka/tertutup
2. Mengenali teorema
Bolzano Weierstrass
III
1.
2.
3.
4
IV
1.
MATERI POKOK
4
1. Definisi persekitaran suatu
titik di R
2. Definisi himpunan terbuka
3. Definisi himpunan tertutup
4. Sifat-sifat himpunan terbuka
5. Sifat-sifat himpunan terbuka
1. Karakteristik Himpunan
terbuka
2. Karakteristik Himpunan
tertutup
3. Teorema sel bersarang
4. Teorema Bolzano
Weierstrass
Mengenali himpunan 1. Himpunan Cantor
Cantor
2. Liput terbuka
Mengenali pengertian 3. Himpunan kompak
liput terbuka
Mengenali himpunan
yang kompak
Membuktikan
1. Teorema K € R kompak
INDIKATOR PENCAPAIAN HASIL PERKULIAHAN
5
Mahasiswa dapat :
1. menentukan persekitaran suatu titik di R
2. menyelidiki suatu himpunan apakah terbuka atau tidak
3. menyelidiki suatu himpunan apakah tertutup atau tidak
4. menyebutkan sifat-sifat himpunan terbuka
5. menyebutkan sifat-sifat himpunan tertutup
Mahasiswa dapat :
1. menulis karakteristik himpunan terbuka
2. menulis karakteristik himpunan tertutup
3. menyebutkan sifat sel bersarang
4. menerangkan teorema Bolzano Weierstrass
Mahasiswa dapat :
1. menerangkan pengertian himpunan Cantor
2. menjelaskan pengertian liput terbuka suatu himpunan
3. membuktikan suatu himpunan kompak
Mahasiswa dapat :
himpunan adalah
kompak
2. Mengenali Teorema
Heine-Borel
Mengenali ruang metrik
jika dan hanya jika K
tertutup dan terbatas
2. Teorema Heine-Borel
1. menerangkan hubungan antara himpunan kompak dan himpunan
tertutup dan terbatas
2. menerangkan teorema Heine-Borel
1. Ruang metrik
1. Mengenali fungsi
yang kontinu
2. membuktikan suatu
fungsi kontinu
Mengenali hubungan
kekontinuan dan
kekompakan
1. Kekontinuan pada suatu
titik
2. Kekontinuan pada suatu
himpunan
1. Teorema kekontinuan
secara umum
2. Hubungan kontinu dengan
kompak
1. Definisi kontinu seragam
2. Teorema kontinu seragam
3. Teorema barisan fungsi
kontinu
Mahasiswa dapat :
1. menentukan suatu metrik
2. membuktikan suatu himpunan adalah suatu ruang metrik
Mahasiswa dapat :
1. menentukan fungsi yang kontinu pada suatu titik
2. menentukan fungsi yang kontinu pada suatu himpunan
3. menyebutkan sifat-sifat fungsi kontinu
Mahasiswa dapat :
1. membuktikan suatu fungsi adalah kontinu atau diskontinu
2. menerangkan hubungan antara fungsi kontinu dengan himpunan
kompak
Mahasiswa dapat :
1. membuktikan suatu fungsi kontinu adalah seragam
2. menyebutkan hubungan antara fungsi seragam dengan himpunan
kompak
3. menyebutkan barisan dari fungsi kontinu
Mahasiswa dapat :
1. menentukan derivatif fungsi f di c
2. menyebutkan hubungan derivatif di c dengan fungsi kontinu
3. menentukan teorema nilai rata-rata
4. menggunakan teorema nilai rata-rata
5
V
6
VI
7
VII
8
VIII
9
IX
10
11
X
XI
Sda
Mengenali integral
Riemann
12
XII
Membuktikan suatu
fungsi terintegral
Riemann
13
XIII
1. Mengenali integral
1. Jumlah Riemann-Stieltjes
Riemann Stieltjes
atas/bawah
2. Membuktikan suatu
2. Integral Riemann-Stieltjes
fungsi terintegral R-S
atas/bawah
3. f terintegrasi Riemann
1. mengenali fungsi
kontinu seragam
2. membuktikan suatu
barisan fungsi adalah
kontinu
1. Mengenali derivatif
suatu fungsi
2. Menerapkan teorema
nilai rata-rata
1. Derivatif f di c
2. Lemma: bila f mempunyai
derivatif di c, maka f
kontinu
3. Teorema nilai rata-rata
4. Aplikasi teorema nilai ratarata
Sda
1. Jumlah Riemann
atas/bawah
2. Integral Riemann
atas/bawah
3. f terintegral Riemann
1. Sifat-sifat integral Riemann
Sda
Mahasiswa dapat :
1. menghitung jumlah Riemann atas/bawah
2. menentukan integral Riemann atas/bawah
Mahasiswa dapat :
1. menyelidiki apakah suatu fungsi f terintegral Riemann atau tidak
2. menentukan sifat suatu fungsi yang diperoleh melalui integrasi suatu
fungsi yang diketahui
Mahasiswa dapat :
1. menghitung jumlah Riemann-Stieltjes atas-bawah
2. menentukan integral Riemann-Stieltjes atas/bawah
3. menyelidiki apakah suatu fungsi f terintegral Riemann Stieltjes atau
tidak
14
XIV
Stieltjes
Mengenali sifat-sifat
1. Sifat-sifat integral
integral Riemann-Stieltjes
Riemann-Stieltjes
2. Teorema Darboux's
3. Integral improper
Mahasiswa dapat :
1. menyelidiki apakah suatu pasangan integrand dan integrafox,
terintegral Riemann-Stieltjes
2. menentukan sifat suatu fungsi yang diperoleh melalui integral
Riemann Stieltjes
7. Sistem Perkuliahan
: - Metode yang digunakan
- Bentuk Kegiatan
- Evaluasi
8. Referensi
: a. Buku Wajib :
1. Bartle, R.G. and Sherbert, D.R., 1994, Introduction to Real Analysis, John Wiley & Sons, Singapore
2. Rudin, W., 1976, Principles of Mathematical Analysis. McGraw-Hill Book Company, Singapore
b. Buku Anjuran :
1. Bartle, R.G. 1976. The Elements of Real Analysis. John Wiley & Sons, New York
2. Royden, H.L., 1988. real Analysis. Macmillan Publishing Company, New York.
Banjarmasin,
Penyusun,