sistem persamaan aljabar tak-linear

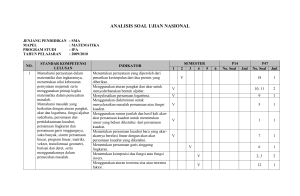
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Metode Newton-Rhapson

Satu persamaan aljabar

Sistem persamaan aljabar tak-linear
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Metode Newton-Rhapson
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Contoh:
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Skema iterasi:
atau

y adalah solusi dari sistem persamaan linear
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Taksiran awal:
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Nilai x(1):
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR
SISTEM PERSAMAAN
ALJABAR TAK-LINEAR

Nilai x(1):

Prosedur diulang sampai kriteria konvergensi
dicapai (10-6);
Solusi eksak x1 = 0,5; x2 = 0,53.

SISTEM PERSAMAAN
ALJABAR TAK-LINEAR



Kelemahan metode Newton: evaluasi matriks
Jacobian secara analitis sangat sulit kalau
persamaan terlalu rumit.
Solusinya: menggunakan finite difference sebagai
pendekatan turunan parsial
ej: vector yang elemen tak-nolnya adalah komponen
kej, yang sama dengan satu.
Pada sisi kanan persamaan di atas komponen ke-j
vektor x dinaikkan sebesar h.