ekuivalen logis - Staffsite STIMATA

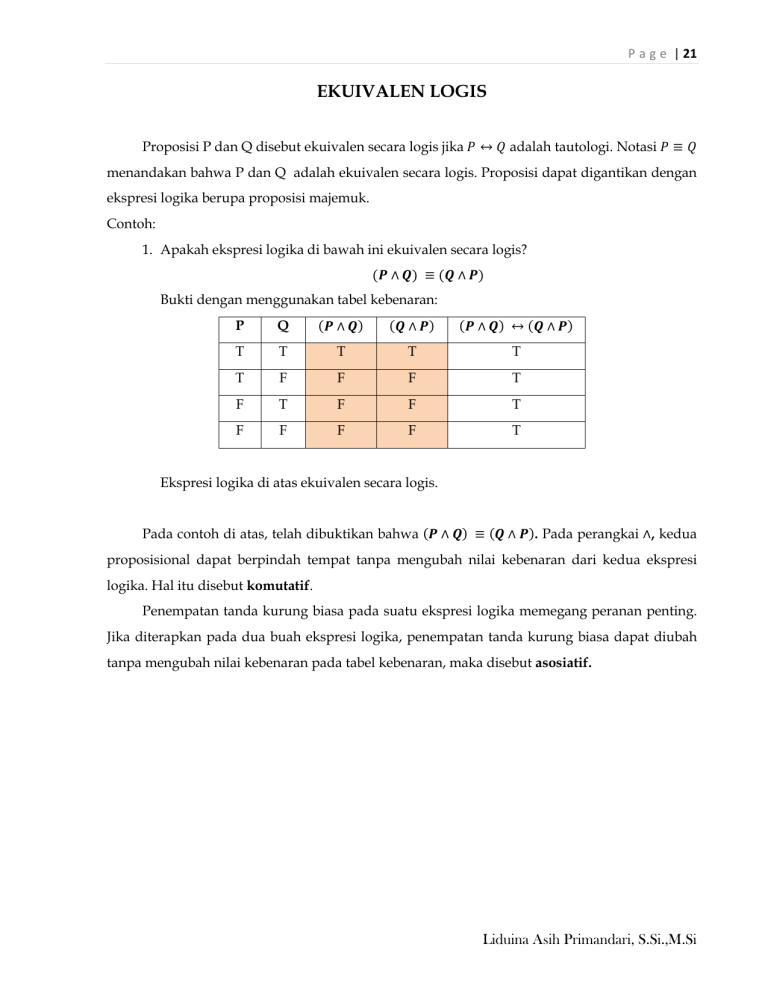
P a g e | 21
EKUIVALEN LOGIS
Proposisi P dan Q disebut ekuivalen secara logis jika 𝑃 ↔ 𝑄 adalah tautologi. Notasi 𝑃 ≡ 𝑄
menandakan bahwa P dan Q adalah ekuivalen secara logis. Proposisi dapat digantikan dengan
ekspresi logika berupa proposisi majemuk.
Contoh:
1. Apakah ekspresi logika di bawah ini ekuivalen secara logis?
𝑷∧𝑸 ≡ 𝑸∧𝑷
Bukti dengan menggunakan tabel kebenaran:
P
Q
𝑷∧𝑸
𝑸∧𝑷
𝑷∧𝑸 ↔ 𝑸∧𝑷
T
T
T
T
T
T
F
F
F
T
F
T
F
F
T
F
F
F
F
T
Ekspresi logika di atas ekuivalen secara logis.
Pada contoh di atas, telah dibuktikan bahwa 𝑷 ∧ 𝑸 ≡ 𝑸 ∧ 𝑷 . Pada perangkai ∧, kedua
proposisional dapat berpindah tempat tanpa mengubah nilai kebenaran dari kedua ekspresi
logika. Hal itu disebut komutatif.
Penempatan tanda kurung biasa pada suatu ekspresi logika memegang peranan penting.
Jika diterapkan pada dua buah ekspresi logika, penempatan tanda kurung biasa dapat diubah
tanpa mengubah nilai kebenaran pada tabel kebenaran, maka disebut asosiatif.
Liduina Asih Primandari, S.Si.,M.Si
P a g e | 22
Contoh:
1. Apakah ekspresi logika di bawah ini asosiatif?
𝑷 ∧ 𝑸 ∧ 𝑹 dan 𝑷 ∧ 𝑸 ∧ 𝑹
P
Q
R
𝑷∧𝑸
𝑸∧𝑹
𝑷∧𝑸 ∧𝑹
𝑷∧ 𝑸∧𝑹
T
T
T
T
T
T
T
T
T
F
T
F
F
F
T
F
T
F
F
F
F
T
F
F
F
F
F
F
F
T
T
F
T
F
F
F
T
F
F
F
F
F
F
F
T
F
F
F
F
F
F
F
F
F
F
F
Terbukti bahwa kedua ekspresi logika di atas asosiatif.
Liduina Asih Primandari, S.Si.,M.Si