fungsi - WordPress.com

5
F U N G S I
Pemahaman tentang konsep fungsi sangat penting dalam mempelajari ilmu
ekonomi, mengingat kajian ekonomi banyak bekerja dengan fungsi. Fungsi dalam
matematika menyatakan suatu hubungan formal antara dua himpunan data. Jika
himpunan data tersebut adalah variabel, maka fungsi dapat dinyatakan sebagai
hubungan antara dua variabel.
5.1. Pengertian dan Unsur-Unsur Fungsi
Fungsi secara sederhana dapat dikatakan sebagai hubungan matematis yang
menyatakan hubungan ketergantungan (hubuungan fungsional) antara satu
variabel dengan variabel lain. Sebuah fungsi dibentuk oleh beberapa unsur
diantaranya variabel, koefisien, dan konstanta. Variabel dan koefisien senantiasa
terdapat di dalam setiap bentuk fungsi, namun tidak demikian dengan konstanta.
Variabel merupakan unsur pembentuk fungsi yang mencerminkan suatu
faktor tertentu. Suatu variabel biasanya dituliskan dalam bentuk huruf-huruf latin,
misalnya x, y, z, dan sebagainya. Berdasarkan kedudukan atau sifatnya, di dalam
setiap fungsi terdapat dua macam variabel yaitu variabel bebas (independent
variable) dan variabel terikat (dependent variable). Nilai variabel terikat
tergantung pada nilai lain misalnya variabel bebas, tetapi tidak sama halnya
dengan variabel bebas.
Koefisien merupakan bilangan atau angka yang terkait pada suatu variabel
dan pada umumnya terletak di depan variabel. Sementara konstanta adalah
bilangan atau angka-angka yang terkadang ikut membentuk sebuah fungsi tetapi
sifatnya berdiri sendiri sebagai bilangan dan tidak terkait dengan suatu variabel
tertentu.
Secara umum, notasi suatu fungsi biasanya dituliskan sebagai
y = f (x) atau z = f (x, y)
dengan x, y, dan z adalah suatu variabel.
1 | Matematika Ekonomi
aswhat.wordpress.com
(5.1)
Contoh 1
a. f (x) = 2x + 1
Karena y = f (x), maka bentuk tersebut dapat dituliskan juga menjadi
y = 2x + 1.
Bentuk f (x) = 2x + 1 maupun y = 2x + 1, keduanya merupakan bentuk fungsi
dengan fariabel bebas x dan variabel terikat y. Angka 2 disebut sebagai
koefisien dalam hal ini koefisien dari x (karena terletak di depan x), sementara
angka 1 disebut sebagai konstanta.
b. g(z) = -z + 3 atau y = -z + 3.
Bentuk g(z) = -z + 3 atau y = -z + 3, juga merupakan fungsi dengan variabel
bebas z. Koefisien z-nya adalah -1, sedangkan konstanta-nya adalah 3. Untuk
menggambarkan bentuk g(z) = -z + 3 ke dalam bidang cartesian maka g(z)
dimisalkan dengan y sedangkan z sama dengan x.
■
Agar pemahaman tentang fungsi tidak terlalu instan, akan diberikan sekilas
tentang tinjaun matematis terhadap fungsi itu sendiri.
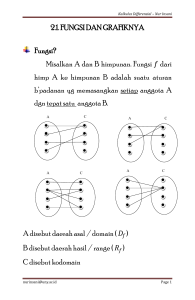
Fungsi biasa juga disebut dengan pemetaan dari himpunan A ke himpunan B,
merupakan relasi khusus yang memasangkan setiap anggota himpunan A dengan
tepat satu anggota himpunan B. Suatu relasi dari himpunan A dan B adalah
himpunan pasangan berurut (a, b) dengan a ∈ A dan b ∈ B.
R = {(a, b) | a ∈ A dan b ∈ B}
(5.2)
Misalkan f adalah suatu fungsi atau pemetaan dari himpunan A ke himpunan
B, maka fungsi f dapat dinotasikan dengan:
f:A→B
(5.3)
Jika a ∈ A dan b ∈ B, dan fungsi f memasangkan a dengan b,maka b disebut peta
atau bayangan dari a. Pada fungsi f : A → B, himpunan A disebut daerah asal
(domain) dari fungsi f dinotasikan dengan Df . Himpunan B disebut daerah kawan
(kodomain) dari fungsi f dinotasikan dengan Kf. Sedangkan himpunan semua peta
A di B disebut daerah hasil (range) dari fungsi f dinotasikan dengan Rf.
2 | Matematika Ekonomi
aswhat.wordpress.com
Contoh 2
Diketahui A = {1, 2, 3, 4}, dan B = {0, 1, 2, 3, 4, 5}.
Jika f : A → B menyatakan “satu kurangnya dari”, maka tentukan daerah hasilnya.
Penyelesaian:
Relasi dari fungsi tersebut adalah = {(1, 2), (2, 3), (3, 4), (4, 5)}
Domain dari f ;
Df = A = {1, 2, 3, 4}.
Kodomain dari f ;
Kf = B = {0, 1, 2, 3, 4, 5}.
Daerah hasil dari f ; Rf = {2, 3, 4, 5}
■
Contoh 3
Misalnya f adalah fungsi dengan aturan f (x) = x2 + 1.
Daerah asalnya, Df = {-1, 0, 1, 2, 3}. Maka,
x = -1, f (-1) = (-1)2 + 1 = 2.
x = 0, f (0) = (0)2 + 1 = 1.
x = 1, f (1) = (1)2 + 1 = 2.
x = 2, f (2) = (2)2 + 1 = 5.
x = 3, f (3) = (3)2 + 1 = 10.
Jadi, daerah hasilnya, Rf = {1, 2, 5, 10}.
Gambar 5.1. Diagram Panah f (x) = x2 + 1.
■
3 | Matematika Ekonomi
aswhat.wordpress.com
5.2. Jenis-Jenis Fungsi
Jika dilihat dari hubungan antara variabel-variabel yang terdapat dalam suatu
fungsi, maka fungsi dapat dibedakan ke dalam dua jenis. Fungsi tersebut yaitu
fungsi eksplisit dan fungsi implisit.
Fungsi eksplisit adalah fungsi yang antara variabel bebas dan variabel terikat
dapat dengan jelas dibedakan.
f (x) = y
(5.4)
Misalnya f (x) = 2x + 3, maka y = 2x + 3. Dalam hal ini, nilai y ditentukan
oleh nilai x. Jadi jika x = 2, maka nilai y = 7. Sedangkan fugsi implisit adalah
fungsi yang antara variabel bebas dan variabel terikatnya tidak mudah untuk
dibedakan. Misalnya fungsi dengan dua variabel, f (x,y), Di sini,
f (x,y) = 0
(5.5)
Misalnya f (x,y) = x2 – 5xy + 6y, maka 0 = x2 – 5xy + 6y. Dari sini, jelas tidak
mudah untuk menetukan berapa nilai x dan nilai y. Harga x dapat diketahui jika
terlebih dahulu ditentukan nilai y, begitu pula sebaliknya. Misalnya lebih dulu
ditentukan x = 1, maka diperoleh y = -1. Sedangkan jika misalnya lebih dulu
ditentukan y = 1, maka x = 2 atau x = 3.
Pembahasan mengenai fungsi matematika tidak terlepas dari pembahasan
tentang titik koordinat. Titik koordinat dapat ditentukan dengan dasar suatu
ukuran yang digunakan dari titik asal (origin point) sebagai titik tolak pengukuran
dan penentuan letak titik dalam gambar grafik dari suatu fungsi. Titik koordinat
(x, y) terdiri dari nilai absis (nilai x) dan nilai ordinat (nilai y).
Dilihat dari bisa tidaknya suatu fungsi dikonstruksi menggunakan operai
aljabar maka fungsi dalam matematika terbagi dua yaitu fungsi aljabar dan fungsi
non-aljabar (fungsi transenden).
5.2.1. Fungsi Aljabar
Fungsi f disebut sebagai fungsi aljabar jika f dapat dikonstruksi menggunakan
operasi aljabar yaitu jumlahan, selisih, hasil kali, hasil bagi, pangkat, ataupun akar
fungsi-fungsi suku banyak. Fungsi aljabar terdiri dari fungsi linear, fungsi
4 | Matematika Ekonomi
aswhat.wordpress.com
kuadrat, fungsi pangkat banyak (pangkat tiga, empat, dan seterusnya), dan fungsi
pecah.
a.
Fungsi Linear
Fungsi linear adalah fungsi yang variabel bebasnya paling tinggi berpangkat
satu. Bentuk umum fungsi linear adalah:
f (x) = ax + b, dengan a, b ∈ R, dan a ≠ 0
(5.6)
Grafik fungsi linear berbentuk garis lurus. Grafik fungsi linear dapat
diperoleh dengan terlebih dahulu mencari hitungan matematisnya seperti langkah
berikut:
1. Menetapkan titik potong fungsi terhadap sumbu-x, dengan memisalkan y = 0.
2. Menetapkan titik potong fungsi terhadap sumbu-y, dengan memisalkan x = 0.
Karena
grafik
fungsi
linear
berbentuk
garis
lurus,
maka
untuk
menggambarkan grafik fungsi linear cukup ditentukan dua titik saja yaitu titik
yang memotong sumbu-x dan titik yang memotong sumbu-y. Sehingga pada
dasarnya langkah yang ditempuh cukup sampai dengan langkah ke-2 saja.
Namun demikian, jika ingin dilihat arah fungsi linear yang dimaksud atau
yang biasa disebut dengan gradien garis (notasi: m), maka dapat dilanjutkan
sampai dengan langkah ke-3.
3. Gradien garis ditentukan oleh persamaan
m
y2  y1
x2  x1
(5.7)
Gradien garis ini ternyata sama dengan nilai a pada f (x) = ax + b. Gradien
garis biasa juga disebut dengan koefisien arah. Nilai gradien garis dapat
berharga positif atau negatif, tergantung dari tanda yang menyertai a dalam
persamaan y = ax + b. Jika a positif maka arah garis dari kiri bawah ke kanan
atas. Sendagkan jika a negatif maka arah garisnya dari kiri atas ke kanan
bawah.
5 | Matematika Ekonomi
aswhat.wordpress.com
Contoh 4
Gambarkan grafik fungsi f (x) = 2x + 3.
Penyelesaian:
 Perpotongan terhadap sumbu-x, maka y = 0.
f (x) = 2x + 3
y = 2x + 3
0 = 2x + 3
x = -2/3.
Jadi, kurva berpotongan di titik (-2/3, 0).
 Perpotongan terhadap sumbu-y, maka x = 0.
y = 2x + 3
y = 2(0) + 3
y = 3.
Jadi,kurva berpotongan di titik (0, 3).
 Nilai gradien m = a = 2.
y
y
-4
4
4
2
2
-2
2
-2
(a)
-4
4
x
x
-2
2
-2
4
(b)
Gambar 5.2. (a). Grafik Fungsi f (x) = 2x + 3; (b). Grafik Fungsi f (x) = -2x + 3.
-4
-4
■
Sebagai perbandingan untuk melihat nilai gradien m, maka diberikan grafik fungsi
f (x) = -2x + 3. Dengan cara yang sama, diperoleh perpotongan terhadap sumbu-x
adalah (3/2, 0), dan perpotongan terhadap sumbu-y adalah (0, 3). Nilai gradien m
= -2. Perhatikan grafik fungsinya pada Gambar 5.2.(b).
6 | Matematika Ekonomi
aswhat.wordpress.com
b.
Fungsi Kuadrat
Bentuk umum fungsi kuadrat adalah
f (x) = ax2 + bx + c,
dengan a, b, c ∈ R, dan a ≠ 0
(5.8)
Grafik fungsi kuadrat berbentuk parabola dengan persamaan y = ax2 + bx + c.
Langkah-langkah untuk menggambarkan grafik fungsi kuadrat adalah sebagai
berikut:
1. Mencari titik potong kurva terhadap sumbu y
2. Mencari titik potong kurva terhadap sumbu x
3. Menetapkan koordinat titik puncak
 b  D 
2
 ,
 , dengan D = b – 4ac.
 2a 4a 
(5.9)
4. Mencari persamaan sumbu simetri, yaitu sumbu yang membagi grafik fungsi
kuadrat menjadi dua bagian yang sama besar.
x
b
2a
(5.10)
Contoh 5
Gambarkan grafik fungsi f (x) = x2 + 5x + 6.
Penyelesaian:
 Titik potong terhadap sumbu-y, maka x = 0.
y = x2 + 5x + 6
y = 02 + 5(0) + 6
y=6
Jadi titik potong terhadap sumbu-y adalah (0,6).
 Titik potong terhadap sumbu-y, maka x = 0.
y = x2 + 5x + 6
0 = x2 + 5x + 6
(x + 2) (x + 3)= 0.
x + 2 = 0 dan x + 3 = 0
x1 = -2
x2 = -3
Jadi titik potong terhadap sumbu-x adalah (-2, 0) dan (-3, 0).
7 | Matematika Ekonomi
aswhat.wordpress.com
 b  D 
 Koordinat titik puncak  ,
.
 2a 4a 
D = b2 – 4ac = (5)2 – 4(1)(6) = 25 – 24 = 1
Selanjutnya,
b 5
5

  dan
2a 2(1)
2
D
1
1


4a 4(1)
4
Sehingga koordinat titik puncaknya adalah (-5/2, -1//4).
 Persamaan sumbu simetri, x 
b
5

2a
2
8y
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
1
2
3
4
5
6
7
x
8
-2
-4 fungsi f (x) = x2 + 5x + 6.
Gambar 5.3. Grafik
-6
c.
Fungsi Pangkat Banyak
■
-8
Fungsi pangkat merupakan fungsi yang variabel bebasnya memiliki pangkat
sebuah bilangan real yang bukan nol. Bentuk umum yang paling sederhana dari
fungsi pangkat adalah
f (x) = xn,
dengan n ∈ R
(5.11)
Fungsi pangkat banyak berangkat dari konsep fungsi polynomial yaitu fungsi
yang memiliki banyak suku pada variabel bebasnya. Bentuk umum fungsi
polynom adalah:
f (x) = anxn + an-1xn-1 + an-2xn-2 +... + a2x2 + a1x1 + a0,
dengan ai ∈ R untuk i = n, n-1, n-2, ..., 2, 1, 0, dan an ≠ 0.
8 | Matematika Ekonomi
aswhat.wordpress.com
(5.12)
Persamaan (5.12) disebut fungsi polynom berderajat n. Jika n = 2, maka
disebut fungsi polynom berderajat 2 dalam hal ini sama dengan fungsi kuadrat.
Jika n = 3 maka disebut fungsi polynom berderajat 3 atau sama dengan fungsi
kubik, dan seterusnya.
Fungsi kubik adalah fungsi yang variabel bebasnya pangkat 3. Bentuk umum
fungsi kubik adalah:
f (x) = ax3 + bx2 + cx + d,
dengan a, b, c, d ∈ R, dan a ≠ 0
(5.13)
Contoh 6
Gambarkan grafik fungsi f (x) = x3 – 2x2 – x + 2.
Penyelesaian:
 Titik potong terhadap sumbu-y, maka x = 0.
y = x3 – 2x2 – x + 2
y = 03 – 2(0)2 – 0 + 2 = 2
Jadi, titik potong kurva terhadap sumbu-y adalah (0, 2).
 Titik potong terhadap sumbu-x, maka y = 0.
x3 – 2x2 – x + 2 = 0
x2 (x – 2) – (x – 2) = 0
(x2 – 1) (x – 2) = 0
(x + 1) (x – 1) (x – 2) = 0
Jadi, titik potong kurva terhadap sumbu-x adalah (-1, 0), (1, 0), dan (2, 0).
y
4
2
x
-4
-3
-2
-1
1
2
3
4
5
-2
Gambar 5.4. Grafik fungsi f (x) = x2 + 5x + 6.
-4
9 | Matematika Ekonomi
aswhat.wordpress.com
■
d.
Fungsi Pecah
Fungsi pecah merupakan fungsi nonlinear yang variabel bebasnya merupakan
penyebut. Fungsi pecah terbagi menjadi fungsi pecah kuadrat dan fungsi pecah
linear. Grafik fungsi pecah berbentuk hiperbola. Untuk menggambarkan garifk
fungsi pecah, maka perlu diketahui ciri-ciri matematisnya apakah termasuk ke
dalam fungsi pecah kuadrat atau fungsi pecah linear.
Langkah-langkah yang digunakan untuk menggambarkan grafik fungsi pecah
pada dasarnya sama dengan grafik fungsi lain yaitu mencari perpotongan grafik
fungsi terhadapa sumbu-x dan sumbu-y. Namun demikian, pada kasus fungsi
pecah, karena grafiknya berbentuk hiperbola maka grafik fungsinya memiliki dua
asimtot yaitu asimtot tegak dan asimtot datar (pada kasus f ( x) 
ax 2  bx  c
,
px  q
memiliki asimtot tegak dan asimtot miring). Bentuk umum dari fungsi pecah
linear adalah:
f ( x) 
ax  b
cx  d
(5.14)
Misalkan akan digambarkan grafik fungsi pecah linear seperti pada
Persamaan (5.14) dengan bentuk umum. Ciri-diri dari fungsi tersebut adalah:
1. Titik potong terhadap sumbu-x diperoleh jika y = 0.
Untuk y = 0, maka x 
b
. Sehingga titik potong terhadap sumbu-x adalah
a
b 
,0 .
 a 
 x, y   
2. Titik potong terhadap sumbu-y diperoleh jika x = 0.
Untuk x = 0, maka y 
 x, y    0,

b
. Sehingga titik potong terhadap sumbu-y adalah
d
b
.
a
3. Asimtot, terdiri dari asimtot tegak dan asimtot mendatar.
Asimtot tegak diperoleh dengan membuat y   , sehingga diperoleh
x
d
. Sedangkan,
c
10 | Matematika Ekonomi
aswhat.wordpress.com
Asimtot mendatar diperoleh dengan membuat x   , sehingga diperoleh
y
a
.
c
Contoh 7
Gambarkan grafik fungsi f ( x) 
2x  3
x 1
Penyelesaian:
 Titik potong terhadap sumbu-y
Jika x = 0, maka y = 3.
Sehingga titik potong yang dimaksud adalah (0,3)
 Titik potong terhadap sumbu-x
3
Jika y = 0, maka x   .
2
 3 
Sehingga titik potong yang dimaksud adalah   , 0 
 2 
 Asimtot tegak: x = -1.
Asimtot mendatar: y = 2.
8y
6
4
2
-8
-6
-4
-2
2
4
6
x
8
-2
-4
Gambar 5.5. Grafik
-6 fungsi f ( x) 
-8
11 | Matematika Ekonomi
aswhat.wordpress.com
2x  3
.
x 1
■
5.2.2. Fungsi Non-Aljabar (Fungsi Transenden)
Fungsi transenden yang akan dibahas pada pokok bahasan ini adalah fungsi
eksponensial dan fungsi logaritma.
a.
Fungsi Eksponensial
Fungsi eksponensial adalah fungsi yang variabel bebasnya merupakan
bilangan pangkat dari suatu konstanta yang tidak nol. Bentuk umum yang paling
sederhana untuuk fungsi eksponensial adalah
f (x) = ax, untuk a ∈ R, dan a ≠ 0
(5.15)
Grafik fungsi eksponensial f (x) = ax memperhatikan ciri-ciri berikut:
1. Jika x   , maka y  f ( x)  
Jika x   , maka y  f ( x)  0
2. Jika x = 0, maka y = 1. Artinya, grafik fungsi eksponensial tersebut hanya
memotong sumbu-y di titik (0, 1), tidak memotong sumbu-x.
3. Asimtot dari fungsi ekponensial adalah sumbu-x. dalam hal ini sebagai asimtot
mendatar.
Contoh 8
Gambarkan grafik fungsi f (x) = 2x.
Penyelesaian:
 Untuk x   , maka y  f ( x)  
x
0
1
2
3
...
∞
y
1
2
4
8
...
∞
 Untuk x   , maka y  f ( x)  0
x
-1
-2
-3
-4
...
-∞
y
1/2
1/4
1/8
1/16
...
∞
12 | Matematika Ekonomi
aswhat.wordpress.com
y
4
2
x
-4
-2
2
4
-2
Gambar 5.6. Grafik fungsi f (x) = 2x.
■
-4
b.
Fungsi Logaritma
Fungsi logaritma adalah fungsi kebalikan (invers) dari fungsi eksponensial
dimana variabel bebasnya merupakan bilangan logaritma. Bentuk umum fungsi
logaritma adalah:
f (x) = alog x
(5.16)
Contoh 9
Gambarkan grafik fungsi: f (x) = 2log x.
Penyelesaian:
Dengan mensubtitusi nilai x ke dalam fungsi, maka diperoleh nilai y seperti yang
terlihat pada tabel berikut:
x
1
2
3
4
5
6
...
10
y
0
1
1,58
2
2,32
2,59
...
3,32
13 | Matematika Ekonomi
aswhat.wordpress.com
y
4
2
x
-4
-2
2
4
-2
Gambar. 5.7. Grafik fungsi f (x) = 2log x.
-4
Soal Latihan
1. Tentukan domain dari masing-masing fungsi berikut:
a. f (x) = 9 – 2x
b.
f ( x)  3 x  1
c.
f ( x) 
1
x3
2. Gambarkanlah grafik fungsi berikut:
a. f (x) = 7 – 3x
b. f (x) = -x2 + 8x – 15
2x  5
4  3x
c.
f ( x) 
d.
f ( x )  3x  2
e. f (x) = 3 + log 2x
14 | Matematika Ekonomi
aswhat.wordpress.com
■