8 Teori Pemodelan elastisitas I ok

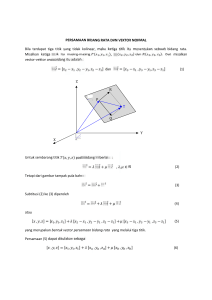
8 TEORI PEMODELAN ELASTISITAS I
Pemodelan adalah permasalahan yang sangat penting dalam geofisika dan memiliki
beberapa kesulitan matematika dalam menentukan sifat-sifat elastik dari tercampur termasuk
terpisah dan material matrix.
8.1. Tinjauan Ikhtisar
Persamaan-persamaan untuk kecepatan gelombang elastik berasal dari rangkaian dasar
teori mekanika klasik. Hal ini menyaratkan material harus homogen. Kecepatan dihubungkan
dengan densitas dan modulus elastik yang mempunyai nilai-nilai unik untuk medium homogen.
Batuan pada umumnya tidak homogen. Batuan yang tak homogen dapat diterapkan dengan
efektif atau ekivalen dengan material homogen, jika dimensinya memenuhi unsur pokok (yaitu
butir-butiran, pori-pori, retakan-retakan, lapisan-lapisan) kecil dibandingkan dengan panjang
gelombang pendek yang signifikan (homogenitas makroskopik). Hudson & Knopoff (1989)
merumuskan: sebuah material mempunyai sifat-sifat variasi skala kecil dengan sudah termasuk
melekatkan material yang berbeda atau telah merembes masuk didalam rekahan, secara
mekanika dapat dikatakan sebagai medium homogen jika eksitasi panjang gelombang lebih
besar dibandingkan dengan skala dalam variasi-variasi struktur atau termasuk ukuran. Sifat
efektif atau sifat makrokopik menghasilkan sifat elastik komponen batuan, struktur batuan dan
variasi antara.
Kelakuan teori elastik batuan diarahkan:
dibawah aspek teoritik dengan deskripsi fisika matematika sifat elastik, fraksi-fraksi
volume dan susunan geometri yang bergantung pada keadaan-keadaan lingkungan (yaitu
tekanan dan temperatur)
dibawah beberapa aspek praktis dengan penerapan dasar untuk memperoleh pemahaman
yang baik dan interpretasi data seismik.
Bagaimana dapat diperoleh hubungan teoritik? Hal ini dapat dimulai dengan model
sederhana yang alamiah, heterogen, struktur batuan yang digambarkan dalam bentuk
matematika. Model tersebut perlu idealisasi yang menekankan pada aspek yang relevan.
Penyeleksian aspek yang relevan dan mempunyai pengaruh bergantung pada maksud kajian.
Hudson dan Knopoff (1989) membedakan dua tipe teori
1.
bahwa perlu diperhatikan batas atas dan batas bawah dalam bentuk nilai-nilai
parameter elastik penyusun medium, dan
2.
perlu diperhatikan dengan penghitungan parameter elastik penyusun medium
Pekerjaan sederhana pada penentuan komposisi material oleh Voigt (1910) dan Reuss (1927)
dijabarkan secara detail harus melibatkan kedua pokok tersebut sebab:
•
hasil berupa solusi eksak untuk penyusun medium harus sesuai dengan model-model
dasar dalam model fisika sederhana, dan
111
•
hasil batas-batas bawah dan atas untuk penyusun medium bukan memenuhi model yang
lain
Sketsa dasar klasifikasi tipe utama teori-teori dasar yang cocok dengan konsep model di
atas disajikan pada gambar 8.1. Beberapa representasi teori-teori yang dijabarkan dan
deskripsinya dititikberatkan pada:
-
asumsi dan konsep model
gagasan pokok tentang perumusan matematika
hasil yang utama
Gambar 8.1. Berbagai teori pendekatan untuk menggambarkan perilaku batuan.
8.2. Model dasar rata-rata spasial dari Voigt (1910) dan Reuss (1927) – dasar teori pada
model lembaran (sheet).
Voigt dan Reuss mengembangkan skema rata-rata untuk mengestimasi konstanta elastis
dari celah mineral tunggal. Jika tak ada orientasi yang sesuai dari butiran mineral dan sumbu
kristalografisnya, maka pori tersebut berlaku secara isotropis. Menurut asumsi pada strain
homogen keseluruhan kumpulan modulus Voigt (subskrip v) adalah:
1
kv = . ( A + 2 B )
3
(8-1)
112
µv = . ( A − B + 3C )
1
5
(8-2)
di mana kv, µv terkait dengan komponen tensor kekakuan dari mineral tersebut.
(8-3)
3A = C11 + C22 + C33
3B = C23 + C31 + C12
(8-4)
3C = C44 + C55 + C66
(8-5)
Menurut asumsi pada stress homogen keseluruhan celah, modulus Reuss (subskrip R) adalah:
1
(8-6)
kR =
3 (a + 2b )
µR =
5
4(a − b ) + 3c
(8-7)
di mana kR, µR terkait dengan komponen tensor kesesuaian mineral.
3a = S11 + S22 + S33
(8-9)
(8-10)
3b = S23 + S31 + S12
3c = S44 + S55 + S66
(8-11)
Untuk penerapan batuan, asumsi model didasarkan pada pemisahan komponen batuan individual
(mineral, bahan pengisi pori) dan susunannya seperti urutan lembaran. Ketebalan relatif
lembaran masing-masinhg sebanding dengan fraksi volume komponen, dimana sifat lembaran
adalah sifat komponen yang terkait. (lihat Gambar 8.1) merupakan suatu keadaan homogenitas
makroskopis yang diasumsikan dengan model ini:
• Strain homogen (modulus Voigt) atau
• Stress homogen (modulus Reuss)
Gambar 8.2.
Komponen individu dianggap isotropik, dimana sifat elastiknya dijabarkan dengan ki dan
µi, dengan indeks komponenya i. Kedua kumpulan persamaan fundamental pada modul
kompresi atau bulk dan modulus geser (shear) adalah:
n
kv = ∑ k i .Vi
(8-12)
i =1
113
n
µv = ∑ µ i .Vi
(8-13)
i =1
n
k R−1 = ∑ k i−1 .Vi
(8-14)
i =1
n
µ R−1 = ∑ µ i−1 .Vi
(8-15)
i =1
dengan Vi adalah fraksi volume komponen i yang terkait dengan volume total.
Jika bahan efektif isotropik, modulus bulk dan modulus geser diberikan oleh batas
bentuk persamaan dengan nilai yang sesuai, maka hubungan Voigt membawa pada bagian
batas atas (maksimum) dan hubungan Reuss pada batas bawah (minimum) (lihat Gambar 8.3).
Nilai real (terukur) ditempatkan antara kedua batas tersebut. Untuk membatasi kisaran nilai
terprediksi tersebut, dua metode yang dapat dipakai:
(1)
(2)
Perhitungan nilai rata-rata (yaitu nilai rata-rata Hill)
Aplikasi batasan lebih lanjut atau prinsip variasi (batas Hashin).
Hill (1952) mengusulkan nilai rata-rata aritmatika dari dua estimasi pada tiap modulus
(disebut juga nilai-nilai Voigt-Reuss-Hill atau VRH, istilah pertama dipakai oleh Chung, 1963,
lihat juga Watt dkk, 1976).
1
kVRH = . (k R + k v )
2
(8-16)
µVRH = . (µ R + µ v )
(8-17)
1
2
Juga rata-rata geometris yang dipakai (misalnya Kumazawa, 1969)
k geom = (k R . k v )
(8-18)
µ geom = (µ R . µ v )1 / 2
(8-19)
1/ 2
Modifikasi model Voigt dilakukan oleh Alexandrof dan Eisenberg (1966), dengan
menggunakan logaritma modulus bulk dan modulus geser.
n
(ln k A ) = ∑
i =1
n
(ln µ A ) = ∑
i =1
V1 . (ln k i )
(8-20)
Vi . (ln µ i )
(8-21)
114
Gambar 8.3 menunjukkan contoh dari dua bahan komponen dengan ketergantungan pada
modulus bahan terkait dan modulus bahan komponen 1 (k/k1) pada fraksi volume V2. Contoh
Rasio modulus bulk diasumsikan k1:k2 = 1:0,2. Kurva untuk model Voigt dan Reuss
memberikan batasan-batasan tersebut. Dalam ruang antara batasan-batasan tersebut, ada kurva
untuk rata-rata VRH dan rata-rata geometric, kedua kurva tersebut hanya memiliki perbedaan
kecil.
Gambar 8.3.
Modifikasi (8-20) dan (8-21) disarankan untuk batuan magmatik oleh Belikov,
Alexandrov dan Rysova (1970). Tabel VIII.1 berisi perbandingan antara modulus bulk terukur
dan terhitung menggunakan persamaan (8-15) dan (8-20).
Crosson dan Lin (1971) memperluas teori Voigt dan Reuss untuk prediksi celah
anisotropis dan menerapkannya pada Dunite dengan menggunakan data petrofabrik dan
konstanta kristal tunggal. Jika memakai model Voigt kesesuaian antara kecepatan terprediksi
dan teramati ada pada kesalahan gelombang kompresi. Kesesuaian terbaik ada pada tekanan di
atas 2 KBar (= 0,2 GPa), ini mungkin disebabkan oleh menurunnya pengaruh seperti cacat
retak mikro pada tekanan lebih tinggi.
Nur (1991) menerapkan konsep Voigt dan Reuss pada pasir berpori dan memodifikasi
porositas dengan memasukkan “porositas kritis” dan kesesuaian memuaskan tercapai pada data
percobaan, dimana porositas kritis tampaknya terkait dengan porositas awal sediment. Model
konseptual dasar dan prinsip proses merata-rata adalah sumber modifikasi dan perkembangan
lebih lanjut, seperti:
115
Pemakaian pada waktu perjalanan seismik (hubungan waktu-rata-rata)
Perkembangan teori bahan berlapis (berlaminasi) yang dijabarkan pada bagian
selanjutnya.
Tabel VIII.1.
8.3.
Teori berdasarkan pada model lembaran atau merata-rata spasial
Bagian ini membahas hubungan waktu-rerata dan padatan berlapisan (laminasi).
Selanjutnya, deskripsi model sederhana untuk batuan patahan, pada asumsi model yang agak
berbeda.
Hubungan waktu-rerata dan “kaitannya”
Wyllie dkk mengusulkan hubungan empiris antara waktu transit interval (kecepatan
timbal balik) dan porositas berdasarkan pada banyaknya percobaan laboratorium dan
penerapan model lembar pada batuan berpori (Lihat Gambar 8.4). Penurunan didasarkan pada
tambahan waktu transit parsial gelombang kompresi untuk matriks murni (seperti silica) dan
bahan pengisi pori murni (seperti air). Untuk kedua bagian dalam model kubus dengan panjang
yang sama untuk matriks dan µ untuk fluida berpori. Tambahan dari kedua waktu transit
menghasilkan apa yang disebut “hubungan waktu-rerata).
∆t = (1 − Φ ). ∆t
m
+ ∆t
f
(8-22)
dengan:
∆t = adalah waktu perjalanan transit batuan.
∆tm= adalah waktu perjalanan transit interval bahan matriks
∆tf =adalah waktu perjalanan transit fluida pori.
Φ = adalah porositas
Satuan waktu perjalanan transit interval adalah µs/m dengan konversi:
1 µs/m = 0,305 µs/ft
1 µs/ft = 3,28 µs/m
Persamaan ini adalah kecepatan timbal balik dan istilah kecepatan menghasilkan persamaan:
116
i 1− Φ Φ
=
+
v
vm
vf
(8-23)
Dari persamaan (8-22) menghasilkan hubungan linier antara waktu perjalanan interval batuan
dan porositas yakni:
Φ=
∆t − ∆t m
∆t f − ∆t m
(8-24)
Persyaratan untuk penggunaan hubungan waktu-rerata adalah pilihan waktu perjalanan interval
yang dijelaskan pada kandungan matriks serta isinya.
Gambar 8.4.
Tabel VIII.2 berisi nilai rata-rata untuk beberapa bahan matrik dan pengisi pori.
Hubungan waktu-rerata yang diterapkan pada kebanyakan kasus biasanya untuk penentuan
porositas “tunggal” pada waktu perjalanan matriks diketahui sebagai satu persamaan dalam
117
sekumpulan persamaan untuk estimasi matriks-porositas. Kesesuaian antara porositas terhitung
dan teramati baik secara khusus yakni:
Waktu perjalanan matriks ditentukan secara individual yang benar.
Batuan dipadatkan atau batuan dibawah kedalaman tertentu (misalnya 2000m)
Kondisi air jenuh (atau kandungan gas rendah).
Tabel VIII.2
Modifikasi empiris disarankan dan diterapkan untuk meningkatkan keakuratan pada hasil yang didapat
antara porositas yang ditentukan dengan log sonic dan data inti laboratorium. Pada formasi yang tak
terkompaksi, persamaan Wyllie menghasilkan porositas yang terlalu tinggi. Situasi yang sebanding ada
pada formasi berserpih. Faktor koreksi c.Δtsh yang mempertimbangkan efek pemadatan atau tekanan
dan suhu dapat ditulis kembali sebagai (lihat Serra, 1984).
∆t − ∆t m
100
Φ COIT =
.
∆t f − ∆t m c . ∆t sh
(8-25)
Karena “relative dari hubungan rerata waktu”, maka diperoleh:
Hubungan linier antara waktu perjalanan (juga kecepatan) dan penyusun batuan (matriks,
lempung, fluida pori), seperti hubungan yang diberikan oleh Han dkk, 1986.
Hubungan non linier antara waktu perjalanan atau kecepatan dan porositas,
∆t = F
ac
. ∆t
= (1 − Φ ) . ∆t
x
m
m
(8-26)
118
dengan Fac adalah “factor formasi akustik” dan x adalah eksponen, tergantung pada tipe batuan (1,60
untuk silica, 1,76 untuk kalsit, 2,00 untuk dolomite).
Jika dicari “hubungan sumber bersama” untuk semua persamaan yang menggambarkan
korelasi kecepatan-porositas atau waktu perjalanan interval–porositas, dapat digunakan “aturan
campuran” yang diterbitkan oleh Korvin (1982). Hubungan antara sifat komposit dan sifat
komponen g1 dan g2 dan fraksi volumnya V1, V2 yakni:
g = g1 .V1a + g 2 .V2a
(8-27)
dengan suatu ekponen a. Dalam kasus batuan berpori, menghasilkan:
g = g m . (1 − Φ ) + g f . Φ a
a
(8-28)
Secara empiris (dan menurut hubungan Raiga-Clemenceau dkk, 1986 dan Raymer dkk, 1980),
diperkenalkan dua eksponen (a,b) sebagai modifikasi untuk kedua fraksi volume yang
menghasilkan suatu “hubungan sumber” digeneralisir.
g = g m . (1 − Φ ) + g f . Φ b
a
(8-29)
Semua persamaan dalam bagian ini adalah kasus khusus dari hubungan umum. Eksponen dan
parameter khusus ditunjukkan pada Gambar 8.5 dalam bentuk “pohon keluarga bersama”.
Gambar 8.5.
119
8.4. Laminated Solid
Teori pertama meneliti properties efektif merupakan penggabungan teori yang dibuat
oleh Rayleigh pada tahun 1982. Bruggemann (1937) memberikan solusi tentang properties
elastik dari sebuah material berlapis yang terdiri dari dua buah komponen. Berdasarkan atas
sistematis dari konstanta lame yang telah dipublikasikan oleh Postma (1955) dan Helbig
(1958), maka dikembangkan teori laminasi (gambar 8.6), teori dan model ini telah
dikembangkan hingga menjadi beberapa komponen (Helbig, 1958; Backus, 1962).
Gambar 8.6. konsep model laminasi
Diawali dengan hubungan stress dan strain untuk medium transverse isotropic.
(8-30)
Model berlaminasi terdiri dari periodik stack lapisan isotropic. Komponen tensor stress dan
strain dibagi menjadi dua bagian :
1.
Class dari konstanta atau ”slowly varying components” (bervariasi tergantung dari panjang
gelombang) : ε 1 , ε 2 , ε 6 , σ 3 , σ 4 , σ 5 . Kekontinuitasan stress dan strains terhadap bidang batas
memerlukan komponen konstanta ini.
2. Class dari variable atau ”rapidly fluctuating components” (berubah dengan ketebalan lapisan
itu sendiri) : ε 3 , ε 4 , ε 5 , σ 1 , σ 2 , σ 6 .
Helbig (1992, 1995) menjelaskan “rapidly fluctuating components” dalam hubungannya
dengan “slowly varying components” :
120
(8-31)
Dari masing-masing komponen stress dan strain yaitu “constant class” untuk memberikan
stress dan strain yang konstan. Ini merupakan hasil langsung dari hubungan rata-rata untuk
menghasilkan campuran yang eratl dari sebuah medium yang terdiri dari tansversely isotropic
berlapis dengan sumbu vertical simetris (x3) :
(8-32)
Tanda kurung <> mengindikasikan nilai rata-rata untuk menyatakan apa yang ada didalamnya.
(8-33)
Dimana (i) mengindikasikan lapisan, c(i) merupakan komponen tensor dan h(i) adalah ketebalan
lapisan. Pada kasus spesial medium terdiri dari dua buah komponen, konstanta Lame λ1 , µ1 , λ 2
dan pecahan volume V1, V2 menyatakan untuk kecepatan dan kelenturan/kekakuan dari arah
utama.
121
(8-34)
(8-35)
(8-36)
(8-37)
(8-38)
(8-38)
Contohnya aplikasi model berlapis; Potma (1955) mempelajari kasus untuk medium berlapis
yang terdiri dari perselingan sandstone dan limestone. Studi dari Pierre shale propertie telah
memperkenalkan oleh White et al (1983).
8.5. A Simple Model for Fractured Rocks
Celah, retak dan kerusakan lainnya dari unsur mineral padat akan merubah sifat
elastiknya secara dramatis, dimana kecepatan gelombang elastic akan berkurang dan besarnya
kecepatan akan tergantung pada besarnya tekanan. Porositas sebagai ratio volume dari
kerusakan (retakan) terhadap volume total tidak dapat menunjukkan efek ini. Retakan kecil
dengan porositas yang kecil dapat merubah kecepatan secara signifikan. Parameter lainnya
dibutuhkan untuk menggambarkan efek fisis dari kerusakan-kerusakan ini. Suatu deskripsi
yang mendekati menggunakan sebuah model sederhana seperti sebuah retakan batuan di
gambarkan pada gambar 8.7 dibawah ini. Dimulai dari sebuah kubus yang padat diasumsikan
bahwa efek dari semua kerusakan (retakan, kerusakan pada batas butiran, kerusakan
intragranular, dan sebagainya) ditunjukkan oleh parameter D.
Gambar 8.7. Sebuah model sederhana untuk batuan dengan kerusakan internal (retakan, patahan dsb)
ditunjukkan oleh parameter D
122
Parameter ini seperti sebuah potongan (cut) dari kedalaman relatif D. Dengan
mengabaikan hubungan antara orde yang lebih tinggi dan efek lainnya dari pori-pori fluida, dapat
dideskripsikan pengurangan dari sifat elasticnya, contohnya pada modulus gelombang bidang
dengan hubungan sederhana :
M = M m .(1 − D )
(8-39)
Dimana M merupakan modulus model batuan dan M m adalah modulus untuk (kerusakan) matrik
material padatnya. Hubungan ini berdasarkan pada asumsi bahwa hanya bagian ”non-cut” dari
cross-section batuan menunjukkan kekakuan. Seperti halnya, parameer D menunjukkan efek dari
patahan, retakan dan kerusakan lainnya atas kecepan gelombang elastik. Jika kita mengabaikan
pengaruh kecil dari kerusakan pada densitas, kecepatan adalah
v p = v m .(1 − D )
1
(8-40)
2
Format dari persamaan ini akan sama dengan perkiraan dalam persamaan Eshelby. Persamaan ini
memberikan yang lebih spesifik dan detail untuk menunjukkan efek patahan dan retakan dalam
sebuha model. Meningkatnya tekanan p mengakibatkan lebih mudah retak atau rusak
ditunjukkan oleh D(p). Untuk ini, dapat diasumsikan bahwa penurunan D dengan kenaikan p
proportional dengan magnitude dari kerusakan, ditulis sebagai;
−
dD
~ D
dp
(8-41)
Diperkenalkan suatu faktor proportional dimana tergantung pada sifat deformasi, sebuah hasil
persamaan diferensial dengan solusi :

p 
D ( p ) = D 0 . exp  − * 
 p 
(8-42)
D0 merupakan retakan awal dari parameter kerusakan pada tekanan p = 0 dan p adalah sebuah
tekanan referensi. Hubungan antara kecepatan, tekanan dan tingkat derajat dari kerusakan awal
adalah :
1

 p  2
(8-43)
v p = v m .1 − D0 . exp − * 
 p 

Karakter eksponennsial dari kecepatan vs hubungan tekanan, termasuk proses akhir,
menyarankan bahwa ”half closure pressure” p 1 harus diperkenalkan. Ini dapat didefinisikan
2
sebagai tekanan yang menyebabkan pengurangan dari parameter kerusakan untuk setengah
retakan awal
 p1 
D
(8-45)
D = 0 = D0 . exp − *2 
 p 
2


Seperti halnya setengah tekanan akhir dan hubungan, untuk tekanan referensi ialah :
(8-46)
p 1 = −(ln 0,5). p * = 0.693. p *
2
123
Contoh sebuah aplikasi dari model sederhana ini untuk mendeskripsikan tentang kecepatantekanan kerusakan sebagai :
Dunite v p = 7,5.[1 − 0,2. exp(− 0,012. p )]
1
Gneiss v p = 6,0.[1 − 0,5. exp(− 0,0087. p )]
Basalt v p = 7,6.[1 − 0,8. exp(− 0,0092. p )]
Breccia
(8-47)
2
1
1
2
(8-48)
2
(8-49)
v p = 4,4.[1 − 0,9. exp(− 0,0097. p )]
1
(8-50)
2
Analisis dari specimen batuan dengan sample KTB
v p ,max = 6500.[1 − 0,60. exp(−0,063. p) − 0,12. exp(−0,005. p )]
v p ,min = 5900.[1 − 0,60. exp(−0,050. p ) − 0,20. exp(−0,005. p )]
1
1
2
(8-51)
2
(8-52)
8.6. Theories Based on Packing of Spheres (kemas bola)
Konsep dari packing of spheres adalah untuk batuan unconsolisdated. Banyak teori yang
mengasumsikan bahwa :
butir adalah berbentuk bola,
butir mempunyai garis tengah yang tunggal, dan
pusat dari lapisan menduduki suatu sistem pola kristal (contoh ; kubus,
hexsagonal)
Asumsi-asumsi ini menentukan kemungkinan dan batasan teori lain. Penurunan model inin
didasarkan pada :
Hubungan stress dan strain untuk kontak butiran partikel dan dasar perilaku stress dan strain
yang berkaitan dengan gaya normal pada titik kontak.
Model kemas bola mengasumsikan kemas kubus dari bola sebagai model untuk
menunjukkan perilaku dari carbon-granule mikrophone, Gassman (1951) mengenalkan paper
klasiknya tentang elastisitas dari sebuah hexagonal packing of spheres. Gambar 8.8
menunjukkan dua bola dari suatu jari-jari R didalam kontak.
Gambar 8.8. Model bola dan perilakunya dari kontak dua spheres dibawah muatan
normal (teori Hertz).
124
Hasil gaya P dalam sebuah deformation dari dua bola menghasilkan pergeseran sebesar s
antara pusat dari dua bola yang bersebelahan dan s = 2.( ∆R ) . Hubungan antara deformation dan
gaya adalah:
 9.(1 − σ s 2 ) 2 p 2 
s = 2.∆R = 

2
2.E s .R


1
3
(8-53)
dengan Es= modulus Young, dan σs = poisson’s ratio
Suatu rangkaian (array) material yang berbentuk kubus dari bola-bola pada tekanan ratarata p dan gaya P yang berkaitan satu sama lain adalah.
P = (2 R) 2 p
deformasinya adalah :
(8-54)
∆R
ε=
R
Substitusi persamaan ini untuk menunjukkan hubungan stress dan strain dan menampilkan
konstanta elastic
1
 3.E 2 . p  3
dp
s

(8-55)
= C 33 = 
2
dε
 8. 1 − σ s 2 
Densitas rata-rata dari model adalah massa dari sebuah bola dibagi volume yang melingkupi
kubus (kasus kering)
(
d=
)
π
(8-56)
ds
6
Kecepatan gelombang longitudinal sepanjang sebuah sumbu dari rangkaian kubus dengan
tekanan rata-rata p adalah :
1
1
1
 3.E s 2 . p  6  6  2

(8-57)
=
.
2 2 
 8.(1 − σ s )   π .d s 
Dengan cara yang sama kecepatan dari gelombang transversal sepanjang sumbu pada rangkaian
kubus dapat dihitung seperti (White, 1983) :
C 
v p =  33 
 d 
[(
2
)
]
1

 2
3
v s = 3. 1 − σ s .E s . p .
(8-58)

 (2 − σ s )(1 + σ s ).π .d s 
Untuk kecepatan gelombang kompresi dengan tekanan permukaan tanah dan kedalaman z adalah
2
2
1
6
1
2
 27
 6
E s .g
(8-59)
vp = 
.
.z 
2
2
 2.π d s 2 1 − σ s 2

dengan g adalah percepatan gravitasi bumi.
Dengan cara yang serupa, kecepatan untuk kemas hexagonal (packing
hexagonal)(Gassman, 1951) atau face-centered cubic packing (Duffy dan Mindlin, 1957) dapat
diperoleh secara umum:
(
)
125
 E s 2 .g

v p = K .
2
2
 (1 − σ s ).d s 
dengan faktor K tergantung pada bentuk array nya:
1
6
( 2π ) ≈ 1.0536
K = (16 ) ≈ 1.0838
π
1
K = 27
Untuk array kubus bola sederhana
2
1
Untuk array hexagonal
2
6
6
(8-60)
(8-61)
(8-62)
Hasil ini valid untuk kemas kering, misalnya tidak ada efek dari pengisian fluida pada pori-pori.
Persamaan ini menunjukkan tiga keterangan :
1. Fungsi kecepatan-tekanan atau kecepatan-kedalaman adalah tidak linier: dibuktikan
dengan percobaan yang hubungannya ialah :
v~ p
1
6
v~z
1
6
Alasan untuk menyutujui teori deformasi pada kontak dari partikel spheres.
2. Tidak sama hasilnya untuk penentuan porositas antara percobaan dan perhitungan. Suatu
kenaikan kecepatan yang berbeda dengan faktor 1,029 sebagai hasil dari penurunan
porositas dari 0,48 (kubus) hingga 0,26 (hexagonal). Ketidaksesuaian ini benar-benar
dikarenakan asumsi dari array pola-pola geometris kristal atau struktur partikel internal.
3. Kecepatan tidak bergantung pada ukuran butir (jari-jari bola); pengaruh dari ukuran butir
untuk sediment adalah ukuran butir-efek porositas (lihat Schon, 1969).
Schon (1969, 1983) menggunakan sebuah statistik untuk menentukan struktur internal sebuah
model bola. Struktur internal adalah yang diuraikan dengan nomor koordinasi η K (nomor dari
kontak untuk satu bola dengan sebelahnya), dan ”sudut struktur α”, ini adalah besar sudut antara
sumbu vertikal x3 dan garis yang tersambung dengan pusat dari dua bola yang bersebelahan.
(Gambar 8.9).
Gambar 8.9. Sifat geometri properties model bola.
a. Definisi sudut struktur α ; b. Sudut struktur α dan nomor koordinasi η K sebagai fungsi porositas,
ditentukan untuk sebuah bola kaca acak (Schon, 1969)
126
Dari hubungan stress-strain untuk kumpulan bola diperoleh kecepatan gelombang
transversal dan longitudinal yang diberikan oleh (Schon, 1969) sebagai:
1
[
]
 1  E  2  6  η  13
1
s
 p  . K  . S ikl m (α , f ) 2
(8-63)
v = 6. 2 .
 d s  1 − σ s 2    G (Φ ) 


dengan Es, σs, adalah modulus young, Poisson’s Ratio, dan ds densitas dari material bola padat, p
adalah tekanan, η K berarti nomor koordinasi, G (Φ ) fungsi yang hanya menentukan porositas,
S ikl (α , f ) adalah komponen dari tensor dengan simetri dari medium isotropic melintang.
m
S ikl (α , f ) tergantung pada sudut struktur α dan koefisien gesekan f pada permukaan bola.
m
Tensor ini disebut ”strukture tensor”. Contoh penggunaan persamaan tersebut diberikan pada
gambar 8.10.
Gambar 8.10.
127