A. Lingkaran Persamaan Lingkaran yang berpusat

Tahun Ajaran 2012
2012-2013/Genap
STKIP Surya
Bab 1. Irisan Kerucut
e=0
e <1
e =1
e >1
A. Lingkaran
Persamaan Lingkaran yang berpusat di titik (0,0)
Pada segitiga siku-siku,
siku, menurut dalil phytagoras berlaku : c2 = a2 + b2
c
b
a
Sekarang perhatikan segitiga siku-siku
siku
OAB yang berada pada gambar lingkaran dibawah ini
ini.
Pada segitiga disamping:
y
AB = x
AB = y
A(x, y)
r
AO = r
y
O
x
B
x
Dalil phytagoras:
OB2 + AB2 = OA2
atau
x2 + y2 = r2
1
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Persamaan ini disebut persamaan lingkaran. Seluruh titik-titik yang memenuhi persamaan ini
akan terletak pada lingkaran yang jari-jarinya r yang berpusat dititik O (0,0).
Persamaan Lingkaran yang berpusat di titik (a,b)
y
C (x,y)
Perhatikan gambar disamping:
BC=y - b
r
AB = x – a
B(x,b)
A(a,b)
BC = y – b
x
AC = r
AB= x - a
Dalil phytagoras:
AB2 + BC2 = AC2
atau
(x - a)2 + (y - b)2 = r2
Ini adalah persamaan lingkaran yang berpusat di titik (a, b) dan memiliki jari-jari r.
atau
+
⇔
⇔
+
⇔
+
⇔
+
+
+
+
2
+
4
4
+
∶
−
+
+
+
4
+
=0
+
+
2
+
=
4
+
4
+
4
=
4
4
−
+
−
+
4
4
− ,−
2
2
−
:! ="
4
+
4
−
2
Created by Edwin Setiawan N.
−
=0
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Kedudukan titik (x1, y1) terhadap lingkaran
1. Terletak didalam lingkaran:
2. Terletak pada lingkaran:
3. Terletak diluar lingkaran:
#
#
#
$
$
$
− %& + #
− %& + #
− %& + #
$
$
$
− '& < !
− '& = !
− '& > !
Hubungan Garis Lurus dengan lingkaran
1. Garis memotong lingkaran pada dua titik lingkaran
2. Garis memotong/menyinggung pada satu titik lingkaran
3. Garis tidak memotong lingkaran lingkaran
Garis memotong lingkaran
pada dua titiktitik
Garis menyinggung
lingkaran
Garis tidak memotong
lingkaran
Garis Singgung Lingkaran
Garis yang melalui titik (a,b) dan menyinggung lingkaran yang berpusat di titik O
P (a, b)
l
O (0, 0)
3
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Dari gambar diatas tampak bahwa garis OP dan garis l saling tegak lurus.
misal m1 adalah gradient garis OP: m1 =
b
a
dan m2 adalah gradient garis l maka
m1m2 = −1
m2 =
−1
m1
m2 =
−a
b
Persamaan garis singgungnya:
y − b = m2 ( x − a)
y −b =
−a
( x − a)
b
y −b =
−ax a 2
+
b
b
by − b 2 = −ax + a 2
ax + by = a 2 + b 2
ax + by = r 2
Dengan cara yang sama seperti cara diatas maka garis singgung melalui titik (x1, y1) dan
menyinggung lingkaran yang berpusat di titik (a, b)
( x − a )( x1 − a ) + ( y − b )( y1 − b ) = r 2
Apabila diketahui gradien garis singgungnya misalnya m, maka persamaan garis singgung
pada lingkaran yang berpusat di (0, 0) dapat dicari sebagai berikut:
Persamaan garis singgung: y = mx + n
4
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Persamaan lingkaran: x2 + y2 = r2
Substitusikan y = mx + n kedalam x2 + y2 = r2
x2 + (mx + n)2 = r2
x2 + m2x2 + 2mnx + n2 - r2 = 0
(1+ m2)x2 + 2mnx + n2 - r2 = 0
kasus menyinggung berarti D = 0
b2 - 4ac = 0
(2mn)2 - 4 (1 + m2)(n2 - r2) = 0
4m2n2 - 4(n2 - r2 + m2n2 - m2r2) = 0
m2n2 - n2 + r2 - m2n2 + m2r2 = 0
-n2 + r2 + m2r2 = 0
n2 = r2 + m2r2
n = ± r 1 + m2
Maka persamaan garis singgungnya: y = mx ± r 1 + m 2
Apabila lingkarannya berpusat di (a, b):
(x - a)2 + (y - b)2 = r2
maka persamaan garis singgungnya:
y − b = m( x − a ) ± r 1 + m 2
Contoh-contoh soal
1. Tunjukkan bahwa titik P (6,-8) terletak pada lingkaran x2 + y2 = 100
Jawab
Titik P (6,-8) berarti x = 6 dan y = -8 kemudian substitusikan ke x2 + y2
5
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
62 + (-8)2 = 36 + 64 = 100 karena hasilnya 100 berarti titik P terletak pada lingkaran
2. Tentukan persamaan garis singgung yang melalui titik A (0, -10) pada lingkaran (x - 3)2 +
(y + 5)2 = 36
Jawab
Titik A (0, -10) berarti x1 = 1 dan y1 = 4
Persamaan lingkaran (x - 3)2 + (y + 5)2 = 36
Persamaan garis singgungnya:
(x - 3) (x1 - 3) + (y + 5) (y1 + 5) = 36
(x - 3) (0 - 3) + (y + 5) (-10 + 5) = 36
-3(x - 3) -5(y + 5) = 36
-3x + 9 - 5y - 25 - 36 = 0
3x + 5y + 42 = 0
3. Tentukan persamaan garis singgung yang melalui titik P (2, 1) pada lingkaran x2 + y2 - 2x
+ 4y - 5 = 0
Jawab
P (2,1) berarti x1 = 2 dan y1 = 1
Persamaan lingkaran: x2 + y2 - 2x + 4y - 5 = 0 berarti A = -1, B = 2, C = -5
Persamaan garis singgung:
xx1 + yy1 + Ax + Ax1 + By + By1 + C = 0
2x + y + (-1)x + (-1)(2) + (2)y + (2)(1) – 5 = 0
2x + y – x – 2 + 2y + 2 - 5=0
x + 3y – 5 = 0
4. Tentukan persamaan garis singgung dengan gradient -2 pada lingkaran x2 + y2 = 16!
6
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Jawab
m = -2, r = 4
persamaan garis singgung: y = mx ± r 1 + m 2
y = −2 x ± 4 1 + (−2) 2
y = −2 x ± 4 5
Jadi persamaan garis singgung lingkaran:
y = −2 x + 4 5
y = −2 x − 4 5
5. Tentukan persamaan garis singgung dengan gradient 3 pada lingkaran (x + 2)2 + (y - 3)2 =
25!
Jawab
m = 3, r = 5, a = -2, b = 3
persamaan garis singgung :
y − b = m( x − a ) ± r 1 + m 2
y − 3 = 3( x + 2) ± 5 1 + (3)2
y = 3x + 6 + 3 ± 5 1 + 9
y = 3 x + 9 ± 5 10
6. Tentukan persamaan garis singgung pada lingkaran (x - 4)2 + (y + 5)2 = 36 dan tegak lurus
dengan garis ½x – y = 10!
Jawab
Garis ½x – y = 10 memiliki gradient m1 = ½
karena tegak lurus maka
7
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
m1⋅ m2 = -1
1/2 ⋅ m2 = -1
m2 = -2
jadi gradien garis singgung yang kita cari adalah -2.
a = 4, b = -5, r = 6
y − b = m( x − a ) ± r 1 + m 2
y + 5 = −2( x − 4) ± 6 1 + (−2)2
y = −2 x + 8 − 5 ± 6 5
y = −2 x + 3 ± 6 5
Latihan
1. Tentukan persamaan lingkaran yang berpusat dititik O(0,0) yang berjari-jari
a. 2
b. 3
c. 5
d. 7
2. Tentukan persamaan lingkaran yang berpusat dititik O(1, 2) yang berjari-jari
a. 4
b. 6
c. 8
d. 10
3. Tentukan persamaan lingkaran yang berpusat dititik O(-3,-2) yang berjari-jari
8
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
a. 4
b. 6
c. √10
d. √15
4. Tentukan titik pusat dan jari-jari dari persamaan lingkaran berikut ini
a. (x + 1)2 + (y - 3)2 = 9
b. (x - 5)2 + (y + 4)2 = 25
c. (x - 7)2 + (y + 10)2 = 20
d. (x + 8)2 + (y - 6)2 = 18
5. Tentukan titik pusat dan jari-jari dari persamaan lingkaran berikut ini
a. x2 + y2 + 4x - 10y + 13 = 0
b. x2 + y2 + 4x - 8y - 44 = 0
c. x2 + y2 + 2x - 6y - 15 = 0
d. x2 + y2 + 6x + 6y - 18 = 0
e. x2 + y2 + 4x - 12y - 8 = 0
f. 2x2 + 2y2 - 2x + 6y - 14 = 0
g. 3x2 + 3y2 - 18x + 24y = 0
h. 2x2 + 2y2 - 6x + 4y – 18 = 0
i. 4x2 + 4y2 - 12x + 16y - 20 = 0
j. 5x2 + 5y2 - 10x + 15y - 30 = 0
9
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
6. Periksa apakah titik-titik berikut terletak didalan lingkaran, pada lingkaran atau diluar
lingkaran jika jari-jari lingkaran 8 dengan titik pusat di (0,0)
a. (2, 4)
b. (5, -3)
c. (-7, 5)
d. (-3, -6)
e. (-2, 7)
f. (-5, 6)
g. (9, 1)
h. (4, -4)
i. (10,12)
j. (8, 7)
7. Tentukan persamaan lingkaran berikut:
a. titik pusat (0, 0) melalui titik (3, 4)
b. titik pusat (0, 0) melalui titik (7, 12)
c. titik pusat (0, 0) melalui titik (8, -6)
d. titik pusat (1, -3) melalui titik (4, 0)
e. titik pusat (4, 6) melalui titik (11, -6)
f. titik pusat (3, -5) melalui titik (10, 7)
g. titik pusat (2, -6) melalui titik (-6, 8)
h. titik pusat (-6, -7 ) melalui titik (2, 2)
i. titik pusat (5, 4) melalui titik (0, 16)
j. titik pusat (-7, -10) melalui titik (-5, -12)
10
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Diketahui lingkaran x2 + y2 + 2px + 10y + 9 = 0 mempunyai jari-jari 5 dan
8.
menyinggung sumbu x. Tentukanlah pusat lingkaran tersebut!
9.
Tentukanlah persamaan lingkaran yang berpusat di (1, 4) dan menyinggung garis 3x 4y – 2 = 0.
10.
Tentukanlah jarak titik pusat lingkaran x2 - 4x + y2 + 4 = 0 dari sumbu y.
11.
Jika titik (-5, k) terletak pada lingkaran x2 + y2 + 2x - 5y - 21= 0, tentukanlah nilai k.
12.
Lingkaran dengan persamaan x2 + y2 - 4x + 2y + c = 0 melalui titik (0,-1). Tentukanlah
jari-jari lingkaran tersebut.
13.
Tentukanlah persamaan garis singgung lingkaran x2 + y2 + 10x- 12y + 20 = 0 yang
melalui titik (-9, 1).
14.
Tentukanlah persamaan lingkaran dengan pusat P (3,1) dan menyinggung garis 3x + 4y
+ 7 = 0.
15.
Garis singgung dititik (12,-5) pada lingkaran x2 + y2 = 169 menyinggung lingkaran (x 5)2 + (y - 2)2 = p. Tentukanlah nilai p.
16.
Tentukanlah titik pusat dan jari-jari lingkaran yang melalui titik-titik (5, 0), (0, 5) dan
(-1, 0)
B. Ellips
Unsur Unsur Elips
Elips adalah tempat keduduka titik-titik yang jumlah jaraknya terhadap dua titik tertentu
adalah tetap. Kedua titik tertentu itu disebut titik fokus.
Y
C(0,b)
A(a,0)
F1 ( - c , 0 )
O
P(x,y)
F1 ( c , 0 )
D(0,-b)
11
Created by Edwin Setiawan N.
B(a,0)
X
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Dari gambar diatas, titik F1 dan F2 dan adalah titik fokus elips dan A, B, C, D adalah titik
puncak elips. Elips mempunyai dua sumbu simetri, yaitu :
1. Garis yang memuat fokus dinamakan sumbu mayor. Pada gambar, sumbu mayor elips
adalah AB.
2. Garis yang tegak lurus sumbu mayor di titik tengah disebut sumbu minor. Pada gambar ,
sumbu minor elips adalah CD.
Sedangkan titik potong kedua sumbu elips itu disebut pusat elips.
Elips juga didefinisikan sebagaitempat kedudukan titik-titik yang perbandingan jaraknya
terhadap suatu titik dan suatu garis yang diketahui besarnya tetap. ( e < 1 ). Titik itu disebut
fokus dan garis tertentu itu disebut direktriks.
Gambar diatas menunjukkan sebuah elips dengan :
-
Pusat elips O(0,0) ;
-
Sumbu simetri adalah sumbu x dan sumbu y ;
-
Fokus F1 (-c,0) dan F2 (c,0) ;
-
Sumbu mayor pada sumbu x, puncak A(-a,0) dan B(a,0) , panjang sumbu mayor = 2a
-
Sumbu minor pada sumbu y, puncak C(0,b) dan D(0,-b) , panjang sumbu minor = 2b
-
Eksentrisitas :
-
A.
Direktriks :
e =
x=
a
e
Panjang lactus rectum
c
a
a2
atau x =
c
2b2
=
a
Persamaan elips yang berpusat di O(0,0) dengan fokus pada sumbu-x
Selain diketahui pusat elipsnya, persamaan elips juga ditentukan dari titik fokusnya.
-.$ = /# + 0 & +
-. = /# − 0& +
-.$ + -. = 2%
12
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
/# + 0 & +
+ /# − 0 & +
1/# + 0 & +
2 = 12% − /# − 0 & +
/# + 0 & +
# + 0& +
= 2% − /# − 0 & +
= 4% − 4%/# − 0 & +
+ 20 + 0 +
1%/# − 0 & +
% ## − 0 & +
%
+% 0 +%
−0
#0 − % &
'
+%
2
+ # − 0& +
= 4% − 4%/# − 0& +
20 = 4% − 4%/# − 0 & +
%
= 2%
− 20
+
− 20 + 0 +
2 = #% − 0 &
& = %3 − 2% 0 + 0
= %3 + 0
+%
= %3 − % 0
+%
=% '
= % #% − 0 &
atau
%
+
'
=1
Apabila fokusnya pada sumbu y F1(0, c) dan F2(0, -c), dengan cara yang sama seperti diatas akan
diperoleh:
%
+'
Catatan:
=% '
atau
'
+
%
=1
c = a2 − b2
Contoh 1
Tentukan persamaan elips yang berpusat di O(0,0), fokus (-4,0) dan (4,0) dengan sumbu
mayor 10 satuan.
Jawab :
Fokus di F1 (-4,0) dan F2 (4,0) maka c = 4 ( fokus pada sumbu x )
Panjang sumbu mayor = 10, maka 2a = 10. Sehingga a = 5
b = a2 − c2 =
25 − 16 =
9 =3
Persamaan elipsnya :
13
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
x2 y2
+
=1 ⇔
a2 b2
x2 y2
+
=1 ⇔
5 2 32
x2 y2
+
=1
25 9
x2 y2
+
=1
Jadi persamaan elipnya adalah
25 9
Contoh 2
x2 y2
+
= 1 , tentukan koordinat titik puncak, koordinat titik
Diketahui persamaan elips
16
9
fokus, panjang sumbu mayor, sumbu minor, eksentrisitas, persamaan direktriks dan panjang
lactus rectum !
Jawab :
x2 y2
+
= 1 , diperoleh a2 = 16, maka a = 4; b2 = 9, maka b = 3.
Dari persamaan elips
16
9
c2 = a2 - b2 , sehingga c2 = 16 – 9 =7, maka c =
7.
Dari data diatas diperoleh :
-
Titik puncak (a,0) = (4,0) dan (-a,0)=(-4,0)
-
Titik fokus ( -c,0) = (- 7 ,0 ) dan ( c,0)=(
-
Panjang sumbu mayor = 2a = 2. 4 = 8
Panjang sumbu minor = 2b = 2. 3 = 6
-
Eksentrisitas:
-
Persamaan direktriks : x = e =
-
Panjang lactus rectum =
e =
c
a
=
a
7 ,0 )
7
4
4
16
16
=
=
7
7
7
4
7
2 b2 2.9 18
1
=
=
=4
a
4
4
2
B.
Persamaan elips yang berpusat di P(α, β)
1.
Fokus terletak pada sumbu utama yang terletak pada / sejajar sumbu x
# − 7&
# − 8&
+
=1
%
'
14
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Dengan :
-
Pusat (α, β)
-
Titik fokus di F1 (α-c, β) & F2(α+c, β)
-
Titik puncak (α-a, β) & (α+a, β)
-
Panjang sumbu mayor = 2a
-
Panjang sumbu minor = 2b
-
Persamaan direktriks x = α ±
a2
c
2. Fokus terletak pada sumbu utama yang terletak pada / sejajar sumbu y
# − 7&
# − 8&
+
=1
'
%
Dengan :
-
Pusat (α, β)
-
Titik fokus di F1 (α, β-c) & F2(α,β+c)
-
Titik puncak (α,β-a) & (α,β+a)
-
Panjang sumbu mayor=2a
-
Panjang sumbu minor=2b
-
a2
Persamaan direktriks y = β ±
c
Contoh 1
Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu mayor dan sumbu minor dari
persamaan elips 4 x 2 + 9 y 2 + 16 x − 18 y − 11 = 0
Jawab :
Nyatakan terlebih dahulu persamaan elips tersebut ke dalam bentuk baku
( x −α )
a2
2
+
(y−β)
b2
2
=1
4 x 2 + 9 y 2 + 16 x − 18 y − 11 = 0
15
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
4 x 2 + 16 x + 9 y 2 − 18 y = 11
4 ( x 2 + 4 x ) + 9 ( y 2 − 2 y ) = 11
{
2
{
2
{
4 ( x − 2 ) − 22 } + 9 ( y − 1) − 12 } = 11
2
{
2
4 ( x − 2 ) − 4} + 9 ( y − 1) − 1} = 11
2
2
4 ( x − 2 ) − 16 + 9 ( y − 1) − 9 = 11
2
2
2
2
4 ( x − 2 ) + 9 ( y − 1) = 11 + 16 + 9
4 ( x − 2 ) + 9 ( y − 1) = 36
( x − 2)
2
9
( y − 1)
+
4
2
=1
Dari persamaan diatas diperoleh : α = 2, β = 1, a2 = 9 maka a = 3, b2 = 4 maka a = 2,
c=
a2 − b2 =
32 − 2 2 =
9−4 =
5
-
Pusat ( α, β ) = ( 2,1 )
-
Titik fokus di F1 ( α - c, β ) = ( 2 - 5 , 1 ) & F2 ( α + c, β ) = ( 2 + 5 , 1 )
-
Titik puncak ( α-a, β ) =( 2 - 3, 1 ) = ( -1, 1 ) & ( α + a, β ) = ( 2 + 3, 1 ) = ( 5, 1 )
-
Panjang sumbu mayor = 2a = 2 ⋅ 3 = 6
-
Panjang sumbu minor = 2b = 2⋅ 2 = 4
Latihan
1. Tentukan persamaan elips yang berpusat di O (0, 0) dengan
a. fokus (-4, 0) dan (4, 0) dan sumbu mayor 10
b. fokus (-6, 0) dan (6, 0) dan sumbu mayor 16
c. fokus (-8, 0) dan (8, 0) dan sumbu mayor 20
d. fokus (-10, 0) dan (10, 0) dan sumbu mayor 26
16
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
2. Tentukanlah persamaan ellips yang berpusat di (0, 0) dengan panjang sumbu mayor dan
sumbu minor berturut-turut
a. 8 dan 6
b. 12 dan 8
c. 16 dan 10
d. 20 dan 12
3. Tentukanlah persamaan ellips yang titik apinya terletak pada sumbu x dan simetri
terhadap titik O (0, 0)
a. sumbu panjangnya 10 dan eksentrisitasnya e = 3/5
b. sumbu panjangnya 16 dan eksentrisitasnya e = 3/4
c. sumbu panjangnya 20 dan eksentrisitasnya e = 2/5
d. sumbu panjangnya 30 dan eksentrisitasnya e = 1/3
4. Tentukanlah persamaan ellips yang
a. berpusat di titik (3, -2), sumbu panjang dan sumbu pendek berturut-turut 6 dan 4
b. berpusat di titik (-1, 5), sumbu panjang dan sumbu pendek berturut-turut 8 dan 4
c. berpusat di titik (2, -1), sumbu panjang dan sumbu pendek berturut-turut 10 dan 6
d. berpusat di titik (-6, 9), sumbu panjang dan sumbu pendek berturut-turut 12 dan 8
5. Tentukan koordinat titik puncak, koordinat titik fokus, panjang sumbu mayor, sumbu
minor, eksentrisitas, persamaan direktriks dan panjang lactus rectum pada ellips-ellips
berikut ini
%.
'.
0.
;.
16
25
20
36
+
+
+
+
10
16
12
16
=1
=1
=1
=1
6. Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu mayor dan sumbu minor
dari persamaan elips
17
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
%.
'.
0.
;.
# − 3&
# + 1&
+
=1
9
4
# + 2&
# − 3&
+
=1
20
16
# + 5&
# + 4&
+
=1
18
12
# − 6&
# + 2&
+
=1
25
9
7. Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu mayor dan sumbu minor
dari persamaan elips
a. 4x2 + 8y2 - 8x + 32y + 4 = 0
b. 4x2 + 7y2 + 16x -42y + 51 = 0
c. 3x2 + 6y2 + 6x - 24y + 9 = 0
d. 6x2 + 10y2 - 48x + 60y + 126 = 0
8. Buatlah sketsa ellips 9x2 + 25y2 - 36x + 50y + 164 = 0
9. Tentukanlah persamaan ellips yang memiliki eksentrisitas e = 2/3 dan salah satu titik
apinya F (6, 0).
10. Carilah persamaan garis singgung pada ellips
# + 2&
# + 3&
+
=1
20
5
Pada titik yang ordinatnya -2.
18
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
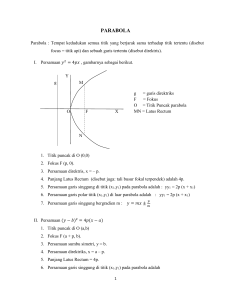
C. Parabola
Parabola adalah tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik dan
suatu garis tertentu
y
P(x, y)
Q (-p, y)
A
x
S
F (p, 0)
O
B
g = -p
Garis g disebut direktrik
Titik F(p,0) disebut titik fokus
Titik O(0,0) disebut titik puncak
FS disebut sumbu simetri (y = 0)
FS = 2p = parameter
Garis AB disebut latus rectum tegak lurus dengan sumbu simetri dan melalui titik F.
Panjang latus rectum=|4p|
Persamaan Parabola
Dengan sumbu x sebagai sumbu simetri
PF = PQ
/# − ?& +
=
+?
1/# − ?& + 2 = # + ?&
19
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
− 2? + ? +
= 4?
=
+2 ?+?
Apabila p>0 maka parabola akan terbuka ke kanan dan p < 0 parabola akan terbuka ke kiri.
Dengan sumbu y sebagai sumbu simetri
= 4?
Apabila p > 0 parabola akan terbuka ke atas dan p < 0 parabola akan terbuka ke kebawah.
Parabola dengan puncak (a,b)
# − '& = 4?# − %&
Titik fokus: F (a + p, b)
Sumbu simetri: y = b
Garis dielektrik: g = a - p
Parabola dengan puncak (a,b)
# − %& = 4?# − '&
Titik fokus: F(a, b + p)
Sumbu simetri: x = a
Garis dierektrik: g = b - p
Latihan
1. Tentukan persamaan parabola jika
a. titik puncaknya di (0, 0) dan titik fokusnya ( 4 , 0 )
b. titik puncaknya di (0, 0) dan titik fokusnya ( 8 , 0 )
c. titik puncaknya di (0, 0) dan titik fokusnya ( 10 , 0 )
d. titik puncaknya di (0, 0) dan titik fokusnya ( 16, 0 )
20
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
e. titik puncaknya di (0, 0) dan titik fokusnya ( -4, 0 )
f. titik puncaknya di (0, 0) dan titik fokusnya ( -8, 0 )
g. titik puncaknya di (0, 0) dan titik fokusnya ( -12, 0 )
h. titik puncaknya di (0, 0) dan titik fokusnya ( -10, 0 )
2. Tentukan persamaan parabola jika
a. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , 8 )
b. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , 10 )
c. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , 12 )
d. titik puncaknya di (0, 0) dan titik fokusnya ( 0, 6 )
e. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , -5 )
f. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , -7 )
g. titik puncaknya di (0, 0) dan titik fokusnya ( 0 , -9 )
h. titik puncaknya di (0, 0) dan titik fokusnya ( 0, -11 )
3. Tentukan persamaan parabola jika
a. titik puncaknya ( 2 , 3) dan titik fokusnya ( 6 , 3 )
b. titik puncaknya ( 1 , 4) dan titik fokusnya ( 7 , 4 )
c. titik puncaknya ( -2 , 2) dan titik fokusnya ( 4 , 2 )
d. titik puncaknya ( 3 , -5) dan titik fokusnya ( 8, -5 )
e. titik puncaknya ( -1 , -1) dan titik fokusnya ( -1 , 5 )
f. titik puncaknya ( -4 , 2) dan titik fokusnya ( -4 , 8 )
g. titik puncaknya ( -2 , -3) dan titik fokusnya ( -2 , -11 )
h. titik puncaknya ( 5 , -6) dan titik fokusnya ( 5 , 0 )
4. Tentukan koordinat fokus dan koordinat titik puncak, persamaan direktriks dan panjang
lactus rectum dari persamaan parabola
a. y2 = 4x
b. 2y2 = -10x
c. 3y2 = 15x
d. y2 = - ½ x
21
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
5. Tentukan koordinat fokus dan koordinat titik puncak, persamaan direktriks dan panjang
lactus rectum dari persamaan parabola
a. x2 = 8y
b. 1/3x2 = -4y
c. 2/3x2 = -8y
d. 3/10x2 = - ½ y
6. Tentukan koordinat titik puncak, titik fokus, persamaan sumbu simetri, persamaan
direktriks dan panjang lactus rectum dari persamaan parabola
a. (y - 2)2 = 4(x - 1)
b. (y + 5)2 = 6(x - 2)
c. (y - 4)2 = -8(x + 3)
d. (y + 9)2 = -10(x – 1/2)
7. Tentukan koordinat titik puncak, titik fokus, persamaan sumbu simetri, persamaan
direktriks dan panjang lactus rectum dari persamaan parabola
a. (x - 4)2 = 12(y - 1)
b. (x + 3)2 = -16(y - 2)
c. (x - 4)2 = 20(y + 3)
d. (x + 5)2 = -18(y – 1/3)
8. Tentukan koordinat titik puncak, titik fokus, persamaan sumbu simetri, persamaan
direktriks dan panjang lactus rectum dari persamaan parabola
a. y2 – 6y – 6x + 15 = 0
b. y2 + 10y – 10x + 55 = 0
c. x2 - 4x - 8y + 6 = 0
d. x2 + 8x + 12y + 4 = 0
22
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
D. Hiperbola
Hiperbola adalah tempat kedudukan titik yang selisih jaraknya terhadap dua titik
tertentu tetap harganya. Dua titik tersebut disebut fokus hiperbola.
Q
P (x, y)
A
F
(-c,0) (-a,0)
G
B
O
(a,0) (c,0)
Titik F (-c, 0) dan G (c, 0) adalah titik fokus hiperbola yang jaraknya 2c.
Titik O (0, 0) disebut pusat parabola
Titik A(-a,0) dan B(a,0) disebut puncak parabola.
Harga c/a disebut eksentrisitas hiperbola.
PF - PG = QG - QF = 2a (tetap)
Persamaan hiperbola dengan pusat (0, 0)
-. = /# + 0& +
-@ = /# − 0& +
-. − -@ = 2%
/# + 0 & +
/# + 0 & +
− /# − 0 & +
= 2%
= 2% + /# − 0 & +
23
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
/# + 0& +
# + 0& +
= 12% + /# − 0& +
2
= 4% + 4%/# − 0 & +
+ 20 + 0 +
+ # − 0& +
= 4% + 4%/# − 0 & +
20 = 4% + 4%/# − 0 & +
+
− 20
40 = 4% + 4%/# − 0& +
0 = % + %/# − 0 & +
0 −% = %/# − 0 & +
#0 −% & = 1%/# − 0& +
2
0
− 2% 0 + %3 = % ## − 0& +
0
− 2% 0 + %3 = %
− 2% 0 + %3 = % #
0
0
−%
#0 − % &
'
%
−
−%
'
=1
−%
−%
=% '
&
− 20 + 0 +
&
− 2% 0 + % 0 + %
= % 0 − %3
= % #0 − % &
Persamaan hiperbola dengan pusat (α, β)
# − 7&
# − β&
−
=1
%
'
24
Created by Edwin Setiawan N.
− 20 + 0 +
Tahun Ajaran 2012-2013/Genap
STKIP Surya
BM
y
x=α
G
B
A
F
y=β
(α, β)
x
O(0, 0)
Asymptot, direktrik dan eksentisitet
Asymptot
Asymptot
Q
P (x, y)
F
B
A
G
O
f
g
Asymptot:
=±
'
%
direktik
25
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
B=−
C=−
%
0
%
0
Eksentrisitas:
D=
0
>1
%
Latihan
1. Tentukan persamaan hiperbola jika
a. titik puncak (-2, 0) dan (2, 0), titik fokus (-4, 0) dan (4, 0)
b. titik puncak (-3, 0) dan (3, 0), titik fokus (-6, 0) dan (6, 0)
c. titik puncak (-3, 0) dan (3, 0), titik fokus (-5, 0) dan (5, 0)
d. titik puncak (-4, 0) dan (4, 0), titik fokus (6, 0) dan (6, 0)
2. Tentukan persamaan hiperbola jika
a. titik puncak (0, -3) dan (0, 3), titik fokus (0, -5) dan (4, 5)
b. titik puncak (0, -2) dan (0, 2), titik fokus (0, -6) dan (0, 6)
c. titik puncak (0, -4) dan (0, 4), titik fokus (0, -7) dan (0, 7)
d. titik puncak (-4, 0) dan (4, 0), titik fokus (6, 0) dan (6, 0)
3. Tentukanlah koordinat titik puncak, koordinat titik fokus, persamaan asimtot, persamaan
direktriks dan panjang latus rectum dari persamaan hiperbola berikut ini
%.
'.
0.
;.
16
12
25
25
−
−
−
−
9
8
9
16
=1
=1
=1
=1
4. Tentukanlah koordinat titik puncak, koordinat titik fokus, persamaan asimtot, persamaan
direktriks dan panjang latus rectum dari persamaan hiperbola berikut ini
26
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
%.
'.
0.
;.
10
36
20
18
−
−
−
−
6
25
15
12
=1
=1
=1
=1
5. Tentukanlah koordinat titik puncak, koordinat titik fokus, persamaan asimtot, persamaan
direktriks dan panjang latus rectum dari persamaan hiperbola berikut ini
%.
'.
0.
;.
# + 1&
# − 2&
−
=1
10
6
# − 3&
# + 5&
−
=1
13
9
# + 7&
# + 4&
−
=1
22
18
# + 2&
# − 4&
−
=1
24
20
6. Tentukanlah koordinat titik puncak, koordinat titik hiperbola, persamaan asimtot,
persamaan direktriks dan panjang latus rectum dari persamaan hiperbola berikut ini
%.
'.
0.
;.
# − 5&
# + 1&
−
=1
11
6
# − 3&
# − 2&
−
=1
40
25
# + 4&
# + 3&
−
=1
30
22
# + 6&
# − 2&
−
=1
24
16
7. Tentukanlah koordinat titik puncak, koordinat titik hiperbola, persamaan asimtot,
persamaan direktriks dan panjang latus rectum dari persamaan hiperbola berikut ini
a. 4x2 - 9y2 + 8x - 18y - 41 = 0
b. 6x2 - 10y2 + 12x + 40y - 94 = 0
c. 4y2 - 16x2 - 16y + 32x - 64 = 0
d. 8y2 - 126x2 + 48y + 120x - 324 = 0
27
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
Soal-Soal Latihan Tambahan
1. Lingkaran yang berpusat di titik O (0, 0) dengan jari – jari
a. x2 + y2 =
d. x2 + y2 = 6
3
b. x2 + y2 = 3
c. x2 + y2 =
3 adalah :
e. x2 + y2 = 9
6
2. Pusat dan jari – jari lingkaran dengan persamaan x2 + y2 – 10 – 2y = 0 berturut – turut
adalah :
a. (10, 2) dan 10
d. (-5, -1) dan 6
b. (5, 1) dan 6
e. (5, 1) dan 6
c. (-5, 1) dan 6
3. Persamaan lingkaran yang berjari – jari 3 dan menyinggung sumbu x
di (3, 0) menyinggung sumbu y di titik (0, 3) adalah :
a. (x – 3)2 + (y – 3)2 = 3
d. (x – 3)2 + (y + 3)2 = 9
b. (x + 3)2 + (y – 3)2 = 3
e. (x – 3)2 + (y – 3)2 = 9
c. (x + 3)2 + (y – 3)2 = 9
4. Persamaan garis singgung lingkaran x2 + y2 = 9 di titik (1, 2) adalah :
a. x + 2y =
d. 2x + y = 5
5
b. x + 2y = - 5
e. 2x + y = - 5
c. x + 2y – 5 = 0
5. Persamaan garis singgung lingkaran x2 + y2 + 5x – 6y + 33 = 0 yang melalui titik (1, -3)
adalah :
a. 7x - 12y – 43 = 0
d. 6x - 7y + 34 = 0
28
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
b. 7x + 12y – 43 = 0
e. 12x + 7y – 24 = 0
c. -7x - 12y + 12 = 0
6. Koordinat titik fokus parabola y2 = -12x adalah :
a. (-12, 0)
d. (0, -3)
b. (-4, 0)
e. (0, -4)
c. (-3, 0)
7. Koordinat tititk puncak parabola y2 + 2x – 6y + 11 = 0
a. (-1, 3)
d. (2, -3)
b. (1, -3)
e. (-2, 6)
c. (2, -6)
8. Persamaan parabola yang berpuncak di titik (4, -2) , mempunyai sumbu simetri garis x =
4 dan panjang lactus rectum 8 adalah : …
a. (y + 2)2 = 8(x – 4 )
d. (y + 2)2 = - 8(x + 2 )
b. (y - 2)2 = 8(x – 4 )
e. (y + 2)2 = - 8(x – 2 )
c. (y + 1)2 = 8(x + 4 )
9. Persamaan garis singgung parabola y2 = 32x yang melalui titik (2, 8) adalah : ..
a. y = 32x + 64
d. y = 2x + 4
b. y = 16x + 2
e. y = x + 2
c. y = 8x + 16
10. Persamaan garis singgung parabola (y - 3)2 = 8(x + 5 ) yang tegak lurus dengan garis x –
2y – 4 = 0
a. 2x + y – 4 = 0
d. 2x - y – 2 = 0
b. 2x + y + 2 = 0
e. 2x - 8y – 5 = 0
c. 2x + y + 8 = 0
29
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
11. Panjang sumbu mayor dari persamaan elips 20x2 + 36y2 = 720 adalah : …
a. 2 5
d. 20
b. 6
e. 36
c. 12
12. Koordinat titik fokus dari persamaan elips 9x2 + 25y2 + 18x – 100y = 116 adalah :
a. (5, 2) dan (-3, 2)
d. (-1, 6) dan (5, 3)
b. (-3, -2) dan (1, 3)
e. (5, 2) dan (-3, 5)
c. (3, 2) dan (5, 2)
13. Persamaan elips dengan pusat O (0, 0).Puncak (10, 0) dan (-10, 0) serta salah satu
fokusnya (-6, 0) adalah : …
a. 10x2 + 6y2 = 60
d. 9x2 + 16y2 = 144
b. 36x2 + 16y2 = 400
e. 9x2 + 25y2 = 225
c. 16x2 + 9y2 = 400
14. Persamaan garis singgung elips 5x2 + 20y2 =100 pada titik (4, 1) adalah :
a. x - y + 5 = 0
d. x + y = -5
b. x + y + 5 = 0
e. -x - y = 5
c. x + y = 5
15. Persamaan garis singgung elips
a. 3x - 6 y = 9
x2 y 2
+
= 1 yang melalui titik (1, - 6 ) adalah :
3
9
d. 6x - 6 y = 1
b. 3x - 6 y = 3
e. x - 6 y = 1
c. 3x - 3 6 y = 11
16. Persamaan garis singgung elips 5x2 + y2 = 5 yang melalui titik A(-2, 1) adalah : …
30
Created by Edwin Setiawan N.
Tahun Ajaran 2012-2013/Genap
STKIP Surya
a. 2x + 3y + 7 = 0
d. 2x - y - 3 = 0
b. 2x - 3y + 5 = 0
e. 2x - y - 5 = 0
c. 3x + 2y + 9 = 0
17. Salah satu asimtot dari hiperbola 9x2 + 16y2 - 54x – 64y - 127 = 0 adalah…
a. 4x - 3y - 18 = 0
d. 3x - 4y 17 = 0
b. 4x - 3y - 6 = 0
e. 3x - 4y – 1 = 0
c. 4x - 3y - 1 = 0
18. Koordinat titik puncak hiperbola x2 - 4y2 - 2x + 24y - 39 = 0 adalah :
a. (1, 2) dan (-1, 2)
d. (1, 0) dan (1, 4)
b. (3, 2) dan (-1, 2)
e. (1, -2) dan (1, -4)
c. (1, 3) dan (-1, 3)
19. Persamaan garis singgung hiperbola 4x2 - y2 - 40x - 4y + 48 = 0 di titik (9, 2) adalah :
a. 4x - y + 21 = 0
d. 9x - 2y - 34 = 0
b. 4x - y - 34 = 0
e. 9x - 2y + 21 = 0
c. 4x - y - 28 = 0
20. Persamaan garis singgung hiperbola 4x2 - y2 + 12 = 0 di titik
(1, 4) adalah :
a. 19x + 11y = 63 dan x – y = -3
b. 19x + 11y = -63 dan x – y = 3
c. 19x - 11y = 63 dan x + y = -3
d. 19x - 11y = -126 dan x + y = 3
e. -19x + 11y = 126 dan -x + y = -3
31
Created by Edwin Setiawan N.