PowerPoint Template - Digilib ITS

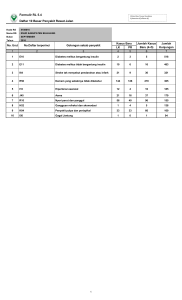
LOGO
SEMINAR TUGAS AKHIR
Oleh :
Rifdatur Rusydiyah
1206 100 045
Dosen Pembimbing :
DR. Subiono, M.Sc
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA
2010
Pendahuluan

Insulin sangat penting untuk menjaga keseimbangan kadar glukosa
darah. Bila terjadi gangguan pada kerja insulin, baik secara
kuantitas maupun kualitas, keseimbangan tersebut akan terganggu
sehingga kadar glukosa darah cenderung naik. Gangguan fungsi
hormon insulin inilah yang dinamakan dengan diabetes melitus.

Diabetes secara umum dibagi menjadi 2 tipe yaitu tipe I dan tipe II

Metode pengobatan yang digunakan pada penderita diabetes tipe I
adalah dengan suntikan insulin atau dengan infus insulin lewat
pompa insulin.

Banyaknya suntikan biasanya ditentukan oleh kadar glukosa
penderita diabetes.
www.themegallery.com

Kurangnya pemonitoran secara terus menerus dalam pemberian
dosis insulin eksogenus pada penderita diabetes mengakibatkan
glukosa darah tidak dapat mencapai nilai normal sehingga biaya
yang dikeluarkan untuk pemberian dosis insulin dapat meningkat.
Sehingga perlu adanya pengendalian optimal pada pemberian insulin
eksogenus pada penderita diabetes.

Berdasarkan permasalahan di atas, pada tugas akhir ini akan
ditentukan pengontrol optimal u*(t) dari masalah tingkat infusi insulin
agar fungsi obyektif dari permasalahan (fungsi biaya) minimal
dengan menggunakan Linear Quadratic Regulator (LQR).
www.themegallery.com
Rumusan Masalah
1. bagaimana menentukan pengontrol optimal u*(t) dari masalah
tingkat infusi insulin agar fungsi obyektif dari permasalahan (fungsi
biaya) minimum
2. bagaimana mensimulasikan bentuk optimal control yang diperoleh
dengan menggunakan software Matlab.
www.themegallery.com
Tujuan dan Manfaat
Tujuan dari Tugas Akhir ini adalah:
1. mendapatkan pengontrol optimal u*(t) dari masalah tingkat infusi
insulin agar fungsi obyektif dari permasalahan (fungsi biaya) minimum
2. mensimulasikan optimal control yang diperoleh dengan menggunakan
software Matlab.
Manfaat yang diharapkan dari Tugas Akhir ini adalah dapat memberikan
informasi bahwa penyelesaian optimal control yang diperoleh dapat
menjadi suatu solusi yang optimal dalam pemberian insulin terhadap
pasien penderita diabetes agar kadar glukosa penderita diabetes dapat
mendekati nilai normal sehingga dapat menekan jumlah biaya yang
dikeluarkan.
www.themegallery.com
Batasan Masalah
1. diabetes yang dibahas dalam Tugas Akhir ini adalah diabetes yang
bergantung insulin (tipe I)
2. metode yang digunakan untuk mendesain pengontrol optimal adalah
metode Linear Quadratic Regulator (LQR).
3. diasumsikan u(t) mempunyai penyelesaian
4. pada model glukosa-insulin Ackerman tingkat suplay glukosa
eksternal p(t) tidak dipertimbangkan untuk desain kontroler atau
p(t)=0
5. diasumsikan m1=0,0009 min-1, m2=0,0031 min-1, m3=0,0415 min-1,
m4=0 dan k=10. Untuk parameter komputasinya adalah g(0)=300,
h(0)=70, i(tf)=0 dengan i=1,2
www.themegallery.com
Diabetes Mellitus
Diketahui jumlah/kadar glukosa dan hormon pada waktu secara berturutturut diberikan oleh fungsi G(t) dan H(t). Maka persamaan keadaan diberikan
oleh:
(1.1)
dengan:
p(t) merupakan tingkat penambahan glukosa dalam darah oleh makanan dan
minuman atau tingkat suplay glukosa eksternal dalam waktu t, dan
u(t) adalah tingkat penambahan insulin oleh injeksi atau tingkat infusi insulin
dalam waktu t.
Pada tugas akhir ini p(t)=0, ini berarti bahwa tidak ada penambahan glukosa
dalam darah oleh makanan dan minuman atau tingkat suplay glukosa
eksternal.
www.themegallery.com
Misalkan tingkat kesetimbangan pada keadaan sehat adalah G0 dan H0 maka
variabel deviasi dari g dan h, masing-masing adalah:
(1.2)
dengan:
dan
dan ditulis persamaan keadaan dalam bentuk linear, bentuk kuadrat dalam
ukuran kecil diabaikan/dihilangkan. Sehingga bentuk linear dari persamaan
keadaan diberikan oleh [3] :
(1.3)
www.themegallery.com
dengan :
m1 = nilai self-removal glukosa; positif
m2 = pengurangan kadar glukosa dengan insulin; positif
m3 = nilai self-removal insulin; positif
m4 = penambahan insulin darah dengan glukosa; lebih besar dari atau sama
dengan nol.
Dalam kasus pasien diabetes tipe I, m4 = 0, hal ini disebabkan karena insulin
tidak dapat diproduksi oleh pankreas.
Fungsi biaya yang digunakan adalah:
(1.4)
dengan k adalah faktor pembobot.
www.themegallery.com
Pembahasan
111
Analisis
dan Keterkontrolan
Click
to Kestabilan
add
Berdasarkan persamaan keadaan pada (1.3) yaitu:
dengan m4=0, maka dapat dibentuk model state space sebagai berikut :
dimana :
,
,
www.themegallery.com
,
1.1 Analisis Kestabilan
Kestabilan suatu sistem dapat dilihat dari nilai karakteristik/eigennya. Untuk
mengetahuinya maka dapat dihitung dengan langkah sebagai berikut :
dengan I adalah matriks identitas dan n adalah nilai eigen dari
matriks A . Dari
didapat:
dan
Karena
,
maka sistem dikatakan stabil.
www.themegallery.com
1.2 Analisis Keterkontrolan
Keterkontrolan dari suatu sistem dapat ditunjukkan oleh matriks terkontrol K
yang ditentukan oleh pasangan matriks (A,B)
dengan :
dan
maka diperoleh :
Terlihat bahwa
Jadi rank K = 2, sehingga sistem terkontrol.
www.themegallery.com
12
Penyelesaian
Optimal
Control dengan LQR
Click
to add
Diketahui persamaan keadaan (1.3) yaitu :
dan performance index seperti pada (1.4) yaitu :
Dari persamaan (1.4) dapat ditentukan persamaan Hamiltoniannya yaitu :
(2.1)
dengan 𝝀 merupakan suatu pengali Lagrange yang belum diketahui. Dari
persamaan Hamiltonian dapat diperoleh persamaan state dan costate sebagai
berikut :
www.themegallery.com
(2.2)
(2.3)
Sedangkan kondisi stasionernya adalah :
(2.4)
Dari persamaan stasioner (2.4) diperoleh kontrol optimal secara umum yang dinyatakan
sebagai berikut :
(2.5)
www.themegallery.com
Dengan substitusi persamaan (2.5) ke dalam persamaan (2.2) diperoleh :
(2.6)
Sehingga dapat dibentuk persamaaan state dan costate (digabungkan) sebagai berikut :
(2.7)
Matriks koefisien dari persamaan (2.7) disebut dengan matriks Hamiltonian.
Dari matriks Hamiltonian di atas dapat ditentukan nilai x* dengan
dan
www.themegallery.com
Untuk mendapatkan nilai x* terlebih dahulu dicari nilai eigen dan vektor eigen
dari matriks A.
Untuk nilai-nilai parameter berikut:
m1=0,0009 min-1, m2=0,0031 min-1, m3=0,0415 min-1, m4=0 dan k=10
diperoleh:
n1=0,0304+0,0077i
n2=0,0304-0,0077i
n3=-0,0304+0,0077i
n4=-0,0304-0,0077i
Dari perhitungan yang telah dlakukan maka dapat diperoleh penyelesaian
x*(t) yaitu:
vj adalah eigenvector dari matriks A yang bersesuaian, dengan eigenvalue nj,
cj merupakan konstanta yang diperoleh dengan memasukkan syarat batas
yang bersesuaian,j=1,2,3,4
www.themegallery.com
Sehingga dapat diperoleh:
www.themegallery.com
13
Hasil
Simulasi
dan Analisisnya
Click
to add
300
kadar glukosa
280
260
g (kadar glukosa)
240
220
200
180
160
140
120
100
0
20
40
60
80
100
120
140
160
180
waktu (menit)
Gambar 3.1 Grafik kadar glukosa g
Pada gambar 3.1 menunjukkan bahwa
grafik kadar glukosa pada penanganan
selama 200 menit terjadi penurunan yang
berarti. Hal ini dapat dilihat pada menit ke67
kadar
glukosa
mendekati
nilai
normalnya, dengan diasumsikan nilai
normal glukosa adalah 100 mg/dl. Hal ini
disebabkan karena adanya penyuplaian
insulin eksogenus sehingga menyebabkan
kadar glukosa yang ada dalam tubuh
penderita diabetes menurun atau mendekati
nilai normalnya.
www.themegallery.com
1000
kadar insulin
900
800
h (kadar insulin)
700
600
500
400
300
200
100
0
20
40
60
80
100
120
140
160
180
waktu (menit)
Gambar 3.2 Grafik kadar insulin h
Pada gambar 3.2 menunjukkan bahwa
grafik kadar insulin pada penanganan
selama 200 menit terjadi perubahan yang
berarti. Hal ini terlihat pada menit pertama
yaitu sampai menit ke-30 kadar insulin naik,
namun setelah menit ke-30 kadar insulin
turun. Hal ini disebabkan karena adanya
tingkat suplay insulin eksogenus yang tinggi
sehingga menyebabkan insulin yang ada
dalam tubuh pasien juga tinggi. Akan tetapi
seiring berjalannya waktu, insulin yang ada
dalam tubuh penderita diabetes juga akan
berkurang.
www.themegallery.com
kontrol
80
70
u (kontrol)
60
50
40
30
20
10
0
20
40
60
80
100
120
140
160
waktu (menit)
180
Gambar 3.3 menunjukkan skenario kontrol
yang
digunakan
dalam
penyuplaian
sejumlah insulin eksogenus pada penderita
diabetes. Pada grafik terlihat bahwa selama
penanganan yaitu 200 menit, tingkat suplay
insulin eksogenus semakin menurun
mendekati nilai nol. Hal ini disebabkan
karena kadar glukosa yang ada pada
penderita diabetes akan semakin menurun
karena adanya penyuplaian sejumlah insulin
eksogenus.
Gambar 3.3 Grafik kontrol u
www.themegallery.com
Kesimpulan dan Saran
 Kesimpulan
Dengan mengumpulkan hasil-hasil dari penyelesaian optimal control dan
simulasi dari bab sebelumnya, maka dapat diperoleh beberapa
kesimpulan sebagai berikut :
1. Pengendali optimal yang diperoleh adalah:
dengan u*(t) adalah tingkat penambahan insulin oleh injeksi atau
tingkat infusi insulin dalam waktu t.
2. Hasil simulasi menunjukkan bahwa kontrol tingkat infusi insulin yang
diberikan dapat mengurangi kadar glukosa yang ada dalam tubuh
pasien penderita diabetes sehingga dapat mencapai nilai normal,
insulin eksogenus yang diberikanpun akan semakin berkurang.
www.themegallery.com
 Saran
Adapun saran dari tugas akhir ini adalah:
1. dalam Tugas Akhir ini digunakan Linear Quadratic Regulator (LQR)
untuk memperoleh pengontrol. Untuk pengembangan sebaiknya
dilakukan pembandingan dengan metode-metode kontrol yang lain
misalkan PID, PMP, maupun yang lainya agar didapatkan pengontrol
yang baik untuk permasalahan tingkat infusi insulin untuk pasien
diabetes.
2. dapat dicari kontrol untuk penyakit yang lain, sehingga dapat
meminimalkan/memaksimalkan indeks performansi yang sesuai
dengan permasalahan yang dibahas.
www.themegallery.com
Daftar Pustaka
[1] Acikgoz, S. U, Diwekar, U.M, (2009), Blood glucose regulation with stochastic optimal control
for insulin-dependent diabetic patient, Chemical Engineering Science, Vol 2009 No. 65 pp
1227-1236.
[2] Chavez, Sanchez , I.Y., Morales-Menendez, R., Chapa, Martinez, S.O., (2009), Glucose optimal
control system in diabetes treatment, Applied Mathematics and Computation, Vol 2009 No. 209
pp 19-30.
[3] Hocking, M., Leslie, (1991), Optimal Control An Introduction to the Theory with Application,
New York, Oxford University Press.
[4] Lewis, F. L., (1995), Optimal Control Second Edition, John Wiley and Sons, Inc.
[5] Noer, S, dr., (1996), Buku Ajar Ilmu Penyakit Dalam jilid I edisi ketiga, Jakarta, FKUI.
[6] Subiono, (2008), Modul Ajar Matematika Sistem. Matematika, Institut Teknologi Sepuluh
Nopember, Surabaya.
[7] Subiono, (2010), Modul Ajar Optimal Control. Matematika, Institut Teknologi Sepuluh Nopember,
Surabaya.
[8] Tjokroprawiro, A, dr., (2006), Hidup Sehat dan Bahagia Bersama Diabetes Melitus, Jakarta, PT
Gramedia Pustaka Utama.
[9] Wahyuni, E, (2009), Pengendalian Optimal Pada Penanganan Tuberkulosis Dua Strain, Skripsi,
Jurusan Matematika FMIPA ITS Surabaya.
www.themegallery.com
LOGO
TERIMA KASIH