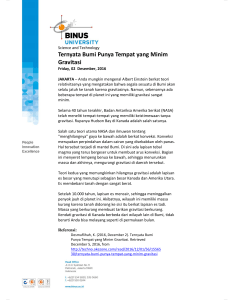
HUKUM GRAVITASI SEMESTA

HUKUM GRAVITASI
SEMESTA
Hukum Newton tentang Gravitasi Semesta
Setiap partikel di alam menarik partikel lain dengan gaya yang besarnya
berbanding langsung dengan hasil kali masa kedua partikel tersebut dan
berbanding terbalik dengan kwadrat jarak antara kedua massa tersebut.
m1
r̂12
F12
F
m1m2
r2
F G
m1m2
r2
konstanta gravitasi
G  6.672  10
r12
m2
F21
11
N  m2
kg 2
mm
F12  G 1 2 2 r̂12
r12
F3  F31  F32
F3  F312  F322  2 F31 F32 cos
F21  F12
Bagaimana gaya gravitasi oleh massa berbentuk bola ?
Gaya gravitasi pada massa m di permukaan bumi :
F G
massa bumi
M Bm
RB2
Jari-jari bumi
Berat Benda dan Gaya Gravitasi
6.672  10
 6.38  10 m
6
Berat benda pada
permukaan bumi
M m
F  G B2
RB
W  mg
g G
11
N  m2
kg 2
 5.98  1024 kg
MB
 9.80 m s 2
2
RB
Bagaimana berat benda pada ketinggian h dari permukaan bumi ?
Jarak benda
ke pusat bumi
M Bm
r2
r  RB  h
F G
F G
M Bm
( RB  h ) 2
W   mg 
g  G
MB
( RB  h ) 2
Semakin jauh dari permukaan bumi, percepatan gravitasi semakin kecil
Hukum Kepler
 Betulkah bumi mengelilingi matahari ?
 Mengapa planet-planet mengelilingi matahari ?
 Bagaimana lintasan orbit planet-planet tersebut ?
1. Semua planet beredar dalam lintasan elip dengan matahari sebagai fokus.
2. Vektor posisi setiap planet terhadap matahari dalam interval waktu yang sama
menyapu luasan yang sama pula.
3. Kwadrat perioda orbit setiap planet sebanding dengan pangkat tiga dari
sumbu mayor lintasannya.
Apakah Hukum Newton tentang Gravitasi sesuai dengan pernyataan ini ?
a
Misal orbit planet terhadap matahari adalah lingkaran :
M M M P M Pv2
G

2
r
r
M
2
G M  2r T 
r
2r T
KM
 4 2
T  
 GM M
2
 3
 r

c
F1
b
F1
Hukum Kepler II dan Kekekalan Momentum Sudut
MP
r
Momen gaya :
v
F
Selalu menuju
ke pusat orbit
MM
τ  r  F  r  F (r )rˆ  0
dL
L  konstan
τ 
0
dt
L  r  p  m (r  v )
?
Luasan yang disapu r dalam selang waktu dt
dA
dr  vdt
r
MM
h

dr
dA  12 rh
h  dr sin 
dA  12 rdr sin   12 r  dr
 12 r  vdt
dA L
rv  2 
dt m
dA L

= konstan
dt 2m
r
Dalam interval waktu yang sama posisi r
menyapu luasan yang sama pula
Medan Gravitasi dan Potensial Gravitasi
Gaya yang dialami oleh massa
uji m di dalam medan gravitasi g
F
g
m
Medan Gravitasi :
Medan Gravitasi bumi : g B 
P
Gaya terpusat
F Selalu menuju ke O
dW  F  dr  F ( r )dr
dr
F  F (r )rˆ
Usaha hanya tergantung
pada posisi awal dan akhir
W  r F ( r )dr
r2
Q
1
r1
U  U f  Ui   r F ( r )dr
r2
r2
1
F
O
r1
RB
F
GM
  2 B rˆ
m
r
m
F
r2
dr
 1 

GM
m
U f  U i  GM B m
B
2
 r  r
r r
 1 1
U f  U i  GM B m     
 rf ri 

r2
1
F
r2
GM B m
rˆ
r2
U (r) 
GM B m
r
1
Energi potensial massa m
pada posisi r
Energi Gerak Planet dan Satelit
v
Mm
r
2
Hukum Newton II : GMm  mv
r2
r
E  12 mv 2  G
r
m
M
1
2
E G
mv 2 
GMm
2r
Mm
Mm   GMm
G
2r
2r
r
Berapakah kecepatan minimum benda untuk lepas dari gravitasi bumi ?
vf  0
M Bm
M Bm
2
1
h  rmak  RB
mv

G


G
2
i
RB
rmak
h
rmak
vi
m
 1
1
vi2  2GM B  
 RB rmak
rmak  
M
vesc



2GM B

RB