BAB VIII KRISTAL SEMIKONDUKTOR TIK : (1) Dapat Membedakan

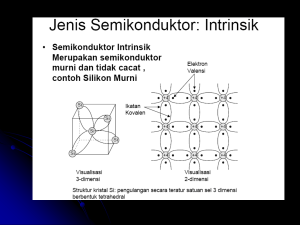
BAB VIII
KRISTAL SEMIKONDUKTOR
TIK
: (1) Dapat Membedakan Jenis Semikonduktor
(2) Dapat Menghitung Konsentrasi Elektron dan Konsentrasi Hole Semikonduktor
(3) Dapat Membedakan Antara Elektron dan Hole
SEMIKONDUKTOR
(1) Intrinsik
Contoh
: Semikonduktor murni (tanpa pengotoran)
: Gol IV A (Si; Ge)
(2) Ekstrinsik : Semikonduktor tidak murni (karena suda disisipi atom-atom lain)
Gol III A dan V A dapat digunakan untuk mengotori semikonduktor murni
Si
Si
Celah Mengukur Celah Energi (Eg)
(1) Penyerapan Langsung
(2) Penyerapan tak Langsung
(1) Penyerapan Langsung
Si memiliki sel primitif berbentuk kubus.
1 buah e yang dipakai bersama
E
h

Eg
(2) Penyerapan Tak Langsung

= phonon

= Foton
Eg ± 
=
Untuk Eg + 
=
berarti phonon dibangkitkan atau
=
berarti fonon diserap
dipancarkan
Untuk Eg - 
Penyerapan langsung
Penyerapan tidak langsung
Persamaan Gerak Elektron Dalam Pita Energi
Kecepatan kelompok untuk beberapa fungsi gelombang yang di bungkus dalam sebuah
paket gelombang dengan vektor gelombang : k adalah : V g
Frekuensi sudut :
d
dk
E


E = energi
6,63 10 34 J .s
2 3,24
h
2
d
dk
Maka: V g
d E
dk 
1 d
E
 dk
1
Ek

Atau V g
(1)
Usaha yang dilakukan oleh medan listrik pada elektron adalah:
E

F .x
 
eE.Vg . t
(2)
Dengan : E = medan listrik
Juga tahu bahwa E dapat ditulis :
E
dE
k
dk
Dari persamaan (1) kita dapatkan:
dE
dk
Vg 
Maka : E
V g
k
Dengan membandingkan persamaan (2) dan (3) kita peroleh:
E
E
Jadi :
eE.Vg t
Vg .
k
k
eE
t

(3)

Atau 
F

k
t
eE
dk
dt
merupakan persamaan gerak e dalam semikonduktor
Massa Efektif (m*)
Apabila kita turunan vg terhadap waktu, maka kita akan memperoleh :
dvg
dt
d2

dkdt
1

1
Dari persamaan gerak kita tahu bahwa
dk / dt
F /
Ingat ! bahwa
. Oleh karena :
dan
Maka :
F = Gaya
pada persamaan (4) akan sama dengan
Dengan m* sering disebut dengan massa efektif.
Perbedaan Antara Hole dan Elektron
d 2 dk
dk 2 dt
(1)
(2)
(3)
(4)
(5)
Konsentrasi elektron (pembawa) dalam semikonduktor murni (intrinsik) terhadap celah energi
(Eg)
Distribusi Fermi-Dirac
Untuk
maka :
Bila energi sebuah elektron dalam pita konduksi adalah :
Dari bab VI kita tahu bahwa : rapat keadaan (density of state) dapat ditulis sebagai berikut
Jumlah elektron dalam pita konduksi adalah :
N
De
g
fe
d
V 2me
2
2
Eg 2
3/ 2
Maka konsentrasi elektronnya adalah :
EK
1
2
(
e
E)
kBT
d
ne
Eg
ne
ne
2
2
1
2
2
3/ 2
2me
2
1
2 me
2
mkT
2 e b2
2 
1
2
EK
(
kBT
3/ 2
kBT
e
E)
e
EK
1
2
e
E
d
kBT
d
Eg
3
2
E K / k bT
e
.................................... (6)
Pers (6) merupakan persamaan yang menyatakan konsentrasi dalam pita konsuksi tetapi belum
merupakan fungsi Eg.
Untuk menjadikan persamaan 6 sebagai fungsi Eg terlebih dahulu kita hitung konsentrasi hole
dalam pita valensi.
Distribusi Fermi-Dirac untuk hole adalah :
fh + fe = 1
fh = 1- fe
fh
fh
fh
fh
eE
eE
e
e
/ K BT
E
E
1
/ K BT
1
e
E
/ K BT
/ K BT
/ K BT
1
1
1
1
1
1
e
E
/ K BT
1
1 e
E / K BT
Untuk (є - µ) >> kB T, maka: f h
Rapat keadaan untuk hole adalah :
e
E
/ K BT
1
e
E
/ K BT
1
E
P.K
EK
EV
P.V
Konsentrasi hole adalah :
EV
np
np
np
1
2
1
2
2
2
3/ 2
2me
2
2me
2
m kT
2 h b2
2 
1
2
EV
3/ 2
EV
e
3
2
e
kBT
EV
(E
e
)
kBT
1
EK 2 e
d
E
kBT
d
/ kbT
Untuk semikonduktor intrinsik : ne = np
Konsentrasi hole
ne n p
mkT
2 e b2
2 
ne n p
kT
4 b 2
2 
ne n p
Ce
3
e
ne
nh
mkT
2 h b2
2 
me mh
3
2
e
4
e
EK EV / kbT
Eg / kbT
maka :
ne2
maka ne
EK / kbT
3
Jika ne = np
ne n p
2
n 2p
np
Ce
Ce
K T
2 B2
2 
Eg / kbT
E g / k bT
3
2
me .mh
3
Eg
2 K BT
3
2
e EV
/ kbT