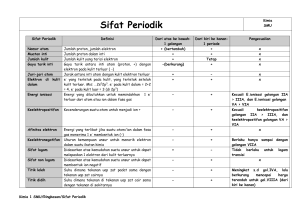
1. Teori Atom (Model Atom)

TRANSPARANSI INTI
Struktur Atom
1. Teori Atom (Model Atom)
1.1 Dalton
Hukum Lavoisier & Proust
⇒
konsep: atom
1.2 Thomson
Hantaran listrik
Tabung
sinar katoda Ö Penemuan elektron
konsep: elektron
Radioaktifitas
1.3 Rutherford
Percobaan berkas sinar α
melalui lempeng tipis.
konsep: inti atom
Sinar α
1.4 Niels Bohr
Spektrum atom H
(deret Balmer, dll.)
Ø
Persamaan Rydberg
konsep: orbit, kulit elektron
1.5 Mekanika Kuantum
Spektrum yang lebih kompleks
untuk atom berelektron banyak.
Penemuan sifat gelombang dari materi
(deBroglie, Heisenberg, Schrodinger)
KIMIA-TPB
konsep: subkulit,
bil. kuantum,
orbital
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
2. Spektrum Atom Hidrogen
2.1 Percobaan Balmer
Sinar putih dilewatkan pada atom H (berupa gas), lalu
didispersikan (lewat prisma) dan ditangkap oleh “layar”.
Diperoleh garis-garis hitam pada beberapa panjang gelombang.
2.2 Percobaan Lymann
Percobaan serupa, tetapi yang diamati adalah daerah UV.
Setelah itu diikuti percobaan Paschen, Bracket, Pfund, Humphrey.
2.3 Persamaan Rydberg
Lymann:
1
1 

= RH  1 − 2 
n 
λ

Balmer:
1
1 1 
= RH  − 2 
λ
4 n 
Secara umum:
 1
1
1 
= R H  2 − 2  atau:
λ
 n1 n2 
3. Teori Atom Niels Bohr & Spektrum Atom H
3.1 Teori Atom Niels Bohr
Niels Bohr menyatakan bahwa:
• Elektron bergerak di sekeliling inti pada lintasan tertentu
(disebut orbit), dengan energi tertentu dengan mengikuti
hukum-hukum mekanika klasik.
• Elektron dapat berpindah dengan menyerap atau memancarkan
energi (dalam bentuk gelombang elektromagnetik, dengan
frekuensi sesuai hukum Planck: E = hν ).
h
• Momentum sudut elektron merupakan kelipatan dari
(sering
2π
disebut sebagai postulat Niels Bohr).
mvr = n
KIMIA-TPB
h
2π
dengan: n = bilangan kuantum
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
3.2 Jari-Jari Atom (Jari-Jari Lintasan Elektron)
Mekanika klasik:
Fc = Fsp
1 e 2 mv 2
=
r
4πε 0 r 2
Postulat Niels Bohr: mvr = …
Dari kedua persamaan di atas, diperoleh jari-jari lintasan elektron:
n 2 h 2ε 0
rn ∼ n 2 ⇒ rn = a0n 2
a0 = 0,529 8
rn =
2
π me
3.3 Energi Elektron
Dari jumlah EK + EP: En = −
me 4
1
13,6
=
−
R
=
−
eV
n2
n2
8n 2 h 2ε o2
En ∼ −
1
n2
3.4 Spektrum H
Elektron yang berpindah dari lintasan n1 ke n2 (n2 > n1), akan
menyerap energi sebesar:
 R  R
 1
1 
∆E = En2 − En1 =  − 2  −  − 2  = R  2 − 2 
 n2   n1 
 n1 n2 
Berdasarkan Planck, gelombang elektromagnetik yang diserap,
akan memiliki frekuensi yang memenuhi hubungan:
∆E = hν = h
c
λ
1 R 1
1 
=  2− 2
λ hc  n1 n2 
3.5 Atom Serupa H (He+, Li2+, O7+)
n 2 h 2ε o
r=
π mZe 2
2 4
mZ e
E=− 2 2 2
8n h ε o
n2
r∼
Z
( 9,1× 10
=−
8 ( 6,6 × 10
Z2
= −13,6 2 eV
n
KIMIA-TPB
−31
−34
kg )(1,6 × 10−19 )
4
Js ) ( 8,85 × 10−12 )
2
2
Z2
n2
Z2
En ∼ − 2
n
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
4. Sejarah Mekanika Kuantum/Mekanika
Gelombang
4.1 Sifat Diskrit dari Gelombang
Gelombang elektromagnet bersifat diskrit. Sifat diskrit ini bisa
menjelaskan percobaan radiasi benda hitam.
E = hν
(E foton)
h = tetapan Planck
ν = frekuensi
(Dapat menjelaskan radiasi benda hitam)
Fenomena sifat diskrit gelombang: efek fotolistrik
Einstein:
hν = Eo + EKe
4.2 Sifat Partikel dari Gelombang
Efek Compton
~~~~~~~~~~
hν = hν’ + EKe
Jika foton dianggap mempunyai massa, maka bisa diturunkan
hubungan momentum foton dengan panjang gelombang foton.
hν = mc2
→
h
= mc
λ
(Einstein + Planck)
4.3 Sifat Gelombang dari Partikel
Hipotesis deBroglie:
λ=
h
mv
Postulat Niels Bohr dapat dinyatakan secara berbeda: bahwa
keliling lintasan elektron merupakan kelipatan bulat dari panjang
gelombang deBroglie.
Percobaan Davisson & Germer:
Berkas elektron dilewatkan pada kisi kristal menghasilkan pola
difraksi elektron. Panjang gelombang yang dihitung berdasarkan
pola difraksi itu bersesuaian dengan panjang gelombang deBroglie.
Lebih jauh lagi, sifat-sifat sistem partikel kecil (yang menunjukkan
sifat kuantum atau sifat gelombang) dapat diturunkan lewat
persamaan gelombang Schrodinger.
KIMIA-TPB
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
5. Teori Atom Mekanika Gelombang
5.1 Penyelesaian Pers. Schrodinger untuk Atom
Persamaan diferensial Schrodinger yang diterapkan untuk atom,
menghasilkan penyelesaian berupa:
• berbagai tingkat energi elektron dalam atom
• fungsi gelombang yang menggambarkan daerah gerak elektron.
Daerah gerak elektron disebut orbital. Orbital adalah daerah
kebolehjadian terbesar untuk menemukan elektron.
Penyelesaian persamaan Schrodinger, memunculkan beberapa
parameter, yang disebut sebagai bilangan kuantum.
Atom H
Atom He dan yang lebih besar
En = ...
En ,l = ...
Ψ n ,l ,m = ...
Ψ n ,l ,m = ...
5.2 Bilangan Kuantum
Bilangan kuantum utama: n = 1, 2, 3, …
Konsep:
Fisik:
menunjuk pada kulit elektron
menggambarkan ukuran orbital
Bilangan kuantum orbital (azimut): l = 0, 1, 2, …, (n-1)
Konsep:
Fisik:
menunjuk pada subkulit
0 s, 1 p, 2 d, dst.
menggambarkan bentuk orbital
Bilangan kuantum magnetik: m = -l, …, 0, …, +l
Konsep:
Fisik:
menunjuk pada orbital dalam subkulit (px, py, pz)
menggambarkan orientasi orbital
Bilangan kuantum spin: s = ±½
Menunjukkan arah spin elektron
KIMIA-TPB
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
5.3 Aturan Pengisian Elektron
Prinsip Aufbau: elektron mengisi orbital dimulai dari subkulit
dengan energi terendah. (Aturan n+´, n, berlaku untuk selain H)
Larangan Pauli: tidak mungkin ada 2 elektron yang mempunyai
spin yang sama dalam orbital yang sama, ATAU
Dalam suatu atom, tidak mungkin ada 2 elektron yang mempunyai
keempat bilangan kuantum yang sama.
Aturan Hund: Pada pengisian orbital-orbital dalam subkulit yang
sama (yang energinya sama), elektron-elektron cenderung tak
berpasangan.
1s
2s
2p
3s
3p
3d
4s
4p
4d
Subkulit p:
4f
__ __ __
px py pz
Aturan subkulit penuh dan setengah penuh: …
5.4 Konfigurasi elektron
Konf.el. ~ suatu cara untuk menggambarkan pengisian elektron
dalam (sub)kulit-(sub)kulit.
11Na:
1s2 2s2 2p6 3s1
Pengisian dalam orbital-orbital digambarkan dalam diagram
elektron.
Elektronvalensi ~ elektron di kulit terluar (dengan n terbesar).
Konfigurasi yang stabil: konfigurasi dengan pengisian sesuai
Aufbau dan Hund, kecuali:
3d4 4s2 → 3d5 4s1
3d9 4s2 → 3d10 4s1
(Aturan penuh dan setengah penuh)
KIMIA-TPB
Departemen Kimia FMIPA ITB
TRANSPARANSI INTI
6. Sifat-Sifat Atom
6.1 Energi Ionisasi
~ energi yang dibutuhkan oleh suatu atom untuk melepaskan
elektron di kulit terluarnya dalam fasa gas.
Energi ionisasi pertama (EI1), energi ionisasi kedua (EI2), dst.
Na(g) → Na+(g) + e
∆H = EI1
Na+(g) → Na2+(g) + e
∆H = EI 2
Ionisasi dimulai dari elektronvalensi, bukan dari elektron dalam
subkulit dengan energi terbesar.
Dari data EI1, EI2, dst. dapat diketahui jumlah elektronvalensi.
Contoh:
6.2 Afinitas Elektron
~ energi yang dilepaskan ketika suatu atom menerima elektron
dalam fasa gas.
Cl(g) + e → Cl-(g)
∆H = − AE
O(g) + e → O-(g)
∆H < 0
O-(g) + e → O=(g)
∆H > 0
∆H < 0
6.3 Sifat Magnet
Sifat magnet ditentukan oleh jumlah elektron tak berpasangan.
Diamagnetik:
tidak ditarik magnet, bahkan kadang agak ditolak.
(tidak memiliki elektron yang tak berpasangan).
Paramagnetik:
ditarik magnet dengan lemah.
Feromagnetik:
ditarik magnet dengan kuat.
KIMIA-TPB
Departemen Kimia FMIPA ITB