Teori Atom dan Cahaya - Dosen Teknik Fisika ITB

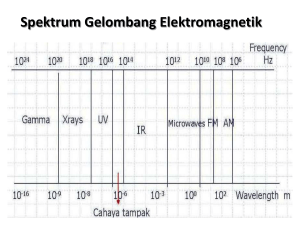
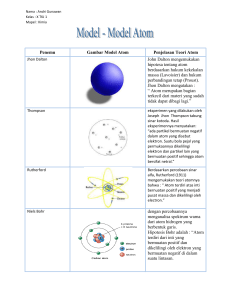
STRUKTUR ATOM
 Model atom Thomson
 Percobaan Geiger & Marsden
 Model atom Rutherford
 Spektral atom
 Model atom Bohr
 Eksitasi atom
 MODEL ATOM THOMSON
-
-
-
-
-
Materi
bermuatan
positip
-
-
Elektron
 Unsur-unsur kimia terdiri dari
atom-atom
 J.J. Thomson menemukan
elektron
 Di dalam atom terdapat elektron
 Atom netral, di dalam atom harus
ada yang bermuatan positip
 J.J. Thomson (1898)
 Atom terdiri dari materi
bermuatan positip yang dikelilingi
oleh elektron-elektron, seperti
fruitcake.
 Kue onde-onde
 PERCOBAAN GEIGER & MARSDEN
 Cara langsung untuk mengetahui apa isi fruitcake,
masukkan jari tangan ke dalamnya, sebagai probe
 Ernest Rutherford mengusulkan menggunakan
partikel alpha sebagai probe
 Partikel alpha = inti Helium bermuatan + 2e
 Massa partikel alpha = 8000 massa elektron
 Hans Geiger dan Ernest Marsden (1911)
menggunakan partikel alpha cepat (2x107 m/s)
 Hamburan partikel alpha akibat tumbukan
dengan lapisan tipis emas diamati dan diukur
 PERCOBAAN GEIGER & MARSDEN
Radioactive substance
Zinc sulfide screen
Microscope
99,86 %
Thin gold foil
Alpha particles
Lead collimator
 MODEL ATOM RUTHERFORD
-
-
+
Neutron
Elektron
-
 Sebagian besar atom adalah ruang
kosong
 Di dalam atom terdapat inti atom
(neutron) yang bermuatan positip
 Hampir semua massa atom
terkonsentrasi di dalam inti atom
 Elektron-elektron berada jauh
dari inti atom
 Rutherford dianggap sebagai
penemu neutron
 Elektron-elektron bergerak seperti
planet-planet mengelilingi
matahari
Formula hamburan Rutherford
N i ntZ 2e 4
N() 
(8o ) 2 r 2 (KE) 2 sin 4 ( / 2)
N()
= Jumlah total partikel alpha per
satuan luas yang sampai di screen
dengan sudut hamburan 
Ni
= Jumlah total partikel alpha yang
sampai di screen
n
= Jumlah atom persatuan volume di
dalam foil
t
= Tebal foil
Z
= Nomor atom dari foil
KE
= Energi kinetik patikel alpha
R
= Jarak screen dari foil
Ukuran inti atom
1 2Ze 2
KE  PE 
4o R
2Ze 2
R 
4o KE
r
Inti atom
KEalpha  7,7 MeV  1,2x1012 J
2(9x109 )(1,6x10 19 ) 2 Z
R 
1,2x10 12
R
PE
 3,8x10 16 Z m
ZCu  79  R Cu  4x10 14 m  10 4 r
KE
Partikel alpha
mv 2
Fc 
r
Atom hidrogen
Fc  Fe  v 
v
r
Fe
Proton
1 e2
Fe 
4o r 2
Elektron
Fc
e
4o mr
Kecepatan elektron
e2
PE  
4o r
2
1
e
KE  mv 2 
2
8o r
Energi total atom hidrogen
e2
E  KE  PE  
8o r
Contoh Soal 3.1
Dari percobaan-percobaan diperoleh bahwa diperlukan energi
sebesar 13,6 eV untuk memisahkan atom hidrogen menjadi sebuah
proton dan sebuah elektron. Ini berarti bahwa energi total atom
hidrogen adalah E = - 13,6 eV. Tentukan kecepatan dan jari-jari orbit
elektron dari atom hidrogen.
Jawab :
e2
r
8o E
E  13,6eV  2,2x1018 J
(1,6x1019 ) 2
11
r

5
,
3
x
10
m
12
18
8(8,85x10 )( 2,2x10 )
v
e

4o mr
1,6x10 19
(9x109 )(9,1x10  31 )(5,3x1011 )
 2,2x106 m / s
Kegagalan model atom klasik
 Mekanik : Hukum Newton
 Listrik : Hukum Coulomb
 Elektromagnetik : partikel
bermuatan yang sedang bergerak
akan meradiasikan energi dalam
bentuk gelombang elektromagnetik
 Energi berkurang, sambil berputar
elektron bergerak menuju proton
 Kenyataannya atom selalu stabil
 Fisika klasik gagal karena
menggunakan pendekatan partikel
murni dan gelombang murni
 SPEKTRAL ATOM
 Atom dalam fasa gas diberi arus listrik
 Setiap atom ternyata mengemisikan gelombang-gelombang
dengan panjang gelombang tertentu (emission line spectra)
 SPEKTRAL ATOM
 Setiap atom juga menyerap gelombang-gelombang dengan
panjang gelombang tertentu (absorption line spectra)
 Panjang gelombang yang diemisikan ternyata sama dengan
panjang gelombang yang diserap
 Diperlukan model atom yang dapat menerangkan
kestabilan atom dan adanya garis-garis spektrum
Deret Spektral Hidrogen
 J.J. Balmer (1885)
 Spektrum cahaya tampak
 H = 656,3 nm
 H = 486,3 nm
 H = 364,6 nm
Formula Balmer :
1
1 
 1
 R 2  2 

n 
2
n  3, 4, 5, 
R = konstanta Rydberg = 0,01097 nm-1
Deret Lyman (ultravoilet)
1
1 
1
 R 2  2 

n 
1
n  2, 3, 4, 
Deret Paschen (inframerah)
1
1 
1
 R 2  2 

n 
3
n  4, 5, 6, 
Deret Brackett (inframerah)
1
1 
 1
 R 2  2 

n 
4
n  5, 6, 7, 
Deret Pfund (inframerah)
1
1 
1
 R 2  2 

n 
5
n  6, 7, 8, 
 MODEL ATOM BOHR
 Niels Bohr (1913)
 Konsep gelombang materi
 Menggunakan pendekatan yang lain,
tetapi hasilnya sama dengan Broglie
v
e
h
h


mv
e
4o mr
4o r
m
r  5,3x1011 m    33x1011 m
  33x1011  2(5,3x1011 )  2 r
 Keliling orbit elektron yang mengelilingi inti atom hidrogen
(proton) ternyata sama dengan panjang gelombangnya
 Terdapat analogi dengan vibrasi/gelombang pada tali/kawat
Sebuah elektron hanya dapat mengelilingi
inti atom bila lintasan orbitnya merupakan
kelipatan bulat dari panjang gelombang
Broglie-nya
n  2rn
nh
e
h

e
4o rn
m
4o rn
 2rn
m
n 2 h 2o
rn 
me 2
n=2
n=4
n  1, 2, 3, 
n = bilangan kuantum
Jari-jari Bohr = ao = r1 = 5,292x10-11 m
rn  n 2 a o
n=8
Tingkat Energi Atom Hidrogen
e2
En  
8o rn
me 4
En   2 2
8 o h
n 2 h 2o
rn 
me 2
 1  E1
 2 2
n  n
n  1, 2, 3, 
E1  2,18x1018 J  13,6 eV
E 2 , E3 , 
Excited states
Ground state
E  0 Elektron bebas
E 5  0,87 x10 19 J  0,54 eV
E 4  1,36x1019 J  0,85 eV
E 3  2,42x10 19 J  1,51 eV
E 2  5,43x1019 J  3,4 eV
E1  21,79x1019 J  13,6 eV
Contoh Soal 3.2
Sebuah elektron bertumbukan dengan sebuah atom hidrogen yang
sedang berada pada tinggat dasar (ground state). Bila atom hidrogen
ini sekarang berada pada tingkat terekstasi (n = 3), berapa energi
yang telah diberikan oleh elektron kepada atom hidrogen dalam
tumbukan tersebut ?
Jawab :
 1
E1 E1
1 
E  E f  E i  2  2  E1  2  2 
nf ni
 nf ni 
n i  1, n f  3, E1  13,6 eV
1
1
E  (13,6 eV) 2  2   12,1 eV
1 
3
Contoh Soal 3.3
Atom-atom hidrogen pada bilangan kuantum yang sangat tinggi
dapat dibuat di laboratorium dan diamati di ruang angkasa.
a). Tentukan bilangan kuantum dimana orbit Bohr = 0,01 mm
b). Hitung energi atom hidrogen tersebut
Jawab :
2
r

a
n
 n
o
a). n
b).
rn

ao
1x105
 435
11
5,29x10
E1  13,6 eV
5
En  2 


7
,
19
x
10
eV
2
n
(435)
Garis-garis Spektrum
 Setelah mendapat energi, tingkat energi atom naik
 Bila tingkat energinya turun, maka tentunya atom akan
mengeluarkan (mengemisikan) energi
 Energi yang diemisikan atom berupa foton
Energi awal – Energi akhir = Energi foton
 1
1 
E i  E f  E1  2  2   hf
nf 
 ni
c
E1  1
1 
f     2  2 

h  nf ni 
E1  1
1 
f    2  2 
h  nf ni 
1
E1  1
1 
   2  2 

ch  n f n i 
 me 4 
  2 2 
4
8

h
E1
me
o
 
7
1

 

1
,
097
x
10
m
R
2 3
ch
ch
8c o h
Deret Lyman
Deret Balmer
Deret Paschen
Deret Brackett
Deret Pfund
nf  1
1
1 
1
 R 2  2 

n 
1
n  2, 3, 4, 
nf  2
1
1 
 1
 R 2  2 

n 
2
n  3, 4, 5, 
nf  3
1
1 
1
 R 2  2 

n 
3
n  4, 5, 6, 
nf  4
1
1 
 1
 R 2  2 

n 
4
n  5, 6, 7, 
nf  5
1
1 
1
 R 2  2 

n 
5
n  6, 7, 8, 
Contoh Soal 3.4
Hitung panjang gelombang terbesar yang terdpat pada deret Balmer
dari atom hidrogen (H).
Jawab :
Deret Balmer :
nf  2
H  n i  3
 1
1
1 
1
1
 R  2  2   R 2  2   0,139R

3 
2
 nf ni 
1
1


 656 nm
7
0,139R 0,139(1,097 x10 )
E=0
n=
n=6
n=5
n=4
n=3
n=2
Series limit
n=1
Lyman series
Balmer series
Paschen series
Brackett series
 EKSITASI ATOM
 Atom akan mampu meradiasikan energi bila berada dalam
keadaan tereksitasi
 Mekanisme 1: Tumbukan dengan partikel lain
 Atom akan menyerap sebagian energi kinetik dari partikel
yang menumbuknya
 Atom akan kembali kekeadaan semula dengan
mengemisikan satu atau lebih foton dalam waktu singkat
(10-8s)
 Mekanisme 2 : Interaksi dengan cahaya pada panjang
gelombang tertentu
 Atom akan kembali kekeadaan semula sambil
mengemisikan foton dengan panjang gelombang yang sama
n=1
Tumbukan dengan
partikel lain
n=2
foton
n=1
Interaksi dengan cahaya
Spektrum absorbsi
foton, 
+
Spektrum emisi
+
foton, 