Spektrum Gelombang Elektromagnetik

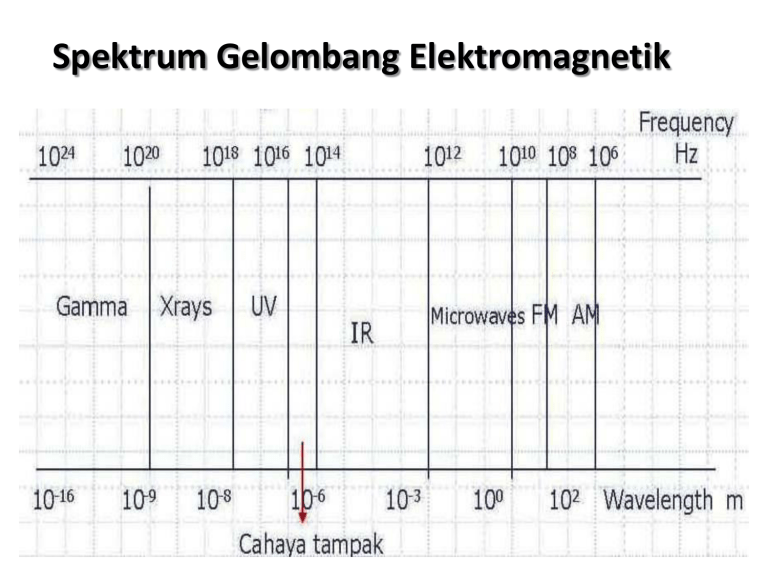
Spektrum Gelombang Elektromagnetik
Hubungan spektrum dengan elektron
• Berkaitan dengan energi
energi cahaya.
energi gerak elektron dan
Keadaan elektron :
 Saat arus dilewatkan melalui gas pada tekanan
rendah, EP atom-atom gas meningkat.
 Keadaan dasar (ground state) : posisi terendah suatu
atom
 Keadaan tereksitasi (excited state) : posisi atom saat
mempunyai EP lebih tinggi dari keadaan pada tingkat
energi dasar.
Lampu Neon
• Saat atom tereksitasi kembali ke keadaan dasar
memancarkan energi dalam bentuk radiasi EM
Cahaya putih
 Tersusun atas bermacam spektrum warna
 Jika dilewatkan prisma, akan terdispersi menjadi
spektrum warna penyusunnya.
Spektrum garis emisi
Ketika arus listrik dialirkan ke dalam tabung vakum yang
mengandung gas Hidrogen pada tekanan rendah
teramati emisi sinar kemerahan
Spektrum Hidrogen
Hγ
6565A
Hδ
4863A
3971A
4103A
4342A
• Spektrum hidrogen sangat menarik karena terdiri dari
sederetan garis-garis yang diberi nama :
 Hα : garis merah
 Hβ : garis hijau
 Hγ : garis biru
 Hδ : garis ungu
Hβ
Hα

n2 
2
2 
n 2 
  b
Deret Balmer

Johann Jakob Balmer (1885) : panjang gelombang dari garis-garis spektral yang waktu itu hanya
menemukan 4 garis spektra yang mengikuti aturan sederhana :
b = 3645,6 A = 3645,6 x 10-10 m
n : bilangan bulat mulai dari 3, 4, 5 dan 6
2


n
  b 2
2 
n 2 
Garis spektrum atom Hidrogen
• Rumus umum :
1 
 1
 R 2  2 

 n n 
1
 n’ = 1 untuk deret Lyman (Ultra Violet)
 n’ = 2 untuk deret Balmer (Cahaya tampak)
 n’ = 3 untuk deret Paschen (Infra merah)
Catatan : Nilai n = n’ + 1 (bilangan bulat)
Model atom Bohr (1913)
• Niels Bohr (1885-1962) ilmuan Denmark yang bekerja dengan
Rutherford.
• Usulannya :
 Secara elektrostatika, elektron harus bergerak mengelilingi
inti agar tidak tertarik ke inti.
Berdasarkan fisika klasik benda yang bergerak memutar akan
melepaskan energi sehingga lama-lama energinya akan
habis/kolaps.
 Jadi elektron harus mempunyai cukup energi untuk berada
dalam gerak konstan mengelilingi inti.
 Gerakan elektron terhadap inti atom dianalogikan seperti
gerakan planet mengelilingi matahari.
Gagasan Bohr dalam menggabungkan
teori klasik dan kuantum
 Hanya ada seperangkat orbit tertentu yang diizinkan
bagi satu elektron dalam atom hidrogen
 Elektron hanya dapat berpindah dari satu lintasan
stasioner ke yang lainnya dengan melibatkan sejumlah
energi menurut Planck
 Lintasan stasioner yang diizinkan mencerminkan sifatsifat elektron yang mempunyai besaran yang khas.
Momentum sudut harus merupakan kelipatan bulat
dari h/2 atau menjadi nh/2.
Besarnya energi yang diperlukan
atau dipancarkan sebesar :
h (tetapan Planck )= 6,6.10-34 J.detik
hc
E  hf 

f (frekuensi foton )= Hz
c (cepat rambat cahaya )= 3.108 m/detik
λ (panjang gelombang foton )= m
EU
hf
El
14
Model atom hidrogen
• Lintasan yang diizinkan untuk elektron dinomori
n
= 1, n = 2, n = 3, dst. dinamakan bilangan kuantum, sedangkan
huruf K, L, M, N dinamakan lintasan
• Jari-jari orbit diungkapkan dengan 12, 22, 32, 42, …n2. Untuk
orbit tertentu dengan jari-jari minimum a0 = 0,53 Å
• Jika elektron tertarik ke inti dan dimiliki oleh orbit n, energi
dipancarkan dan energi elektron menjadi lebih rendah.
M
L
K
+
E3
E2
E1
n3
n2
n1
E1 < E2 < E3
Jari-jari lintasan stasioner
-e
F k
( Ze)(e)
r2
Ze 2
mv 2
k

2
rn
rn
+ Ze
r
rn
kZe 2

mv 2
Katakanlah : v  nh / 2 mrn
kZe 2 4 2 mrn2
n2 h2
n2
rn 


r1
2 2
2
2
n h
4 mkZe
Z
Untuk orbit kecil n  1 dan untuk hidrogen Z  1
h2
r1 
4 2 mke2
 0, 53x1010 m (jari-jari Bohr)
Energi total elektron dalam tiap lintasan adalah sebagai berikut :
 13,6
En 
eV
2
n
Energi elektron pada lintasan :
n = 1  E= -13,60 eV
n = 2  E= - 3,40 eV
n = 3  E= - 1,51 eV
n = 4  E= - 0,85 eV
n = 5  E= - 0,54 eV
n = 6  E= - 0,38 eV
n = 7  E= - 0,28 eV
n = ~  E= - 0 eV
B
E n  2 , B : konstanta numerik dengan nilai 2,179 x 10 -18 J
n
17
Kesuksesan teori Bohr
 Mampu menerangkan spektrum dari atom yang
mempunyai satu elektron pada kulit terluar.
Kelemahan teori Bohr
 Tidak dapat menerangkan spektrum dari atom yang memiliki elektron
lebih dari 1 di kulit terluarnya.
 Tidak dapat menerangkan terjadinya garis spektra tambahan ketika atom
hidrogen diletakkan pada medan listrik atau medan magnet.
 Tidak mampu menghitung besarnya panjang gelombang spektra
tambahan tersebut bahkan tidak mampu meramalkan sama sekali
keberadaan garis itu.