Document

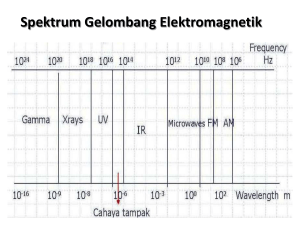
QUANTUM THEORY OF ATOM
Introduction
Gel Cahaya, Foton dan Teori Bohr
Cahaya memberikan informasi mengenai
struktur atom. Untuk mendapatkan gambaran
tersebut, harus dipahami konsep – konsep
terkait :
1. Sifat gelombang dari cahaya
2. Efek kuantum dan foton
3. Teori Bohr untuk atom H
4. Bilangan kuantum dan orbit atom
7|2
Gelombang
Gelombang dicirikan dengan besaran panjang
gelombang dan frekwensi gelombang
Panjang gelombang (l) adalah jarak antara dua
titik identik dalam ruang yang dilewati gangguan
Frekwensi (n) adalah jumlah panjang gelombang
per satuan waktu, dinyatakan dalam satuan Hertz
Copyright © Houghton Mifflin Company. All rights reserved.
7|3
Gelombang
Panjang gelombang dan frekwensi terkait dengan
kecepatan cahaya yaitu (c= 3.00 x 108 m/s).
c = nl
.
7|4
Waves
Copyright © Houghton Mifflin Company. All rights reserved.
7|5
Gelombang
Rentang frekwensi dan panjang gelombang EM dinamakan
digambarkan dalam spektrum gel EM. Gelombang
elektromagnetik merupakan gabungan antara osilasi medan
listrik dan medan magnet
7|6
Efek Fotolistrik
Efek fotolistrik
adalah terjadinya
pelepasan elektron
pada saat logam
disinari dengan
cahaya. Teori
gelombang cahaya
tidak bisa
menjelaskan
peristiwa tersebut
Copyright © Houghton Mifflin Company. All rights reserved.
7|7
Contoh
Garis spetrum hijau dari atom Hidrogen memiliki
panjang gelombang 486 nm. Berapa energi dari
cahaya ini?
E = hn
l = 4.86 nm = 4.86 × 10-7 m
c = nl
c = 3.00 × 108 m/s
E = hc/l
h = 6.63 × 10-34 J  s

 34
8 m
6.63x10 Js  3.00 x 10

hc
s

E

λ
4.86 x 10  7 m

)

)
l = 4.09 × 10-19 J
7|8
Teori Kuantum dari Atom
Pada permulaan tahun 1900, atom hanya difahami terdiri
dari inti bermuatan positif dan dikelilingi oleh elektron yang
bergerak (Rutherford’s model).
Ketidakkonsistenan : Partikel bermuatan yang bergerak
melingkar tersebut akan kehilangan energinya karena
radiasi EM, sehingga elektron akan jatuh ke inti
Kenyataan : atom dalam keadaan stabil
Teori Rutherford tidak bisa menjelaskan spektrum garis
dari atom. Spektrum garis memperlihatkan hanya cahaya
tertentu atau panjang gelombang tertentu yang
dipancarkan oleh atom.
7|9
Spektrum emisi atom Hidrogen
• Tabung sinar hidrogen berisi gas
hidrogen pada tekanan rendah dengan
elektroda pada tiap-tiap ujungnya. Jika
dilewatkan tegangan tinggi (5000 volt),
tabung akan menghasilkan sinar
berwarna merah muda terang.
• Jika sinar tersebut dilewatkan pada
prisma atau kisi difraksi, sinar akan
terpecah menjadi beberapa warna.
Warna yang terlihat merupakan
sebagian kecil dari spektrum emisi
hidrogen. Sebagian besar spektrum tak
terlihat oleh mata karena berada pada
daerah infra-merah atau ultra-violet.
• Kenyataan tsb diyakini berkaitan erat
dengan struktur atom. Spektrum garis
atomik dapat digunakan untuk menguji
kebenaran dari sebuah model atom
Spektrum garis beberapa Atom
7 | 11
Pada 1913, Neils Bohr mengemukaan dua
postulat mengenai :
1. Stabilitas atom Hidrogen
2. Spektrum garis atom Hidrogen
7 | 12
• Model atom Bohr dikemukakan oleh Niels Bohr yang berusaha
menjelaskan kestabilan atom dan spektrum garis atom hidrogen
yang tidak dapat dijelaskan oleh model atom Rutherford.
– di dalam atom hidrogen, elektron hanya dapat
mengelilingi lintasan tertentu tertentu yang diijinkan
tanpa membebaskan (melepaskan) energi. Lintasan
ini disebut lintasan stasioner dan memiliki energi
tertentu yang sesuai.
– elektron dapat berpindah dari satu lintasan ke lintasan
yang lain. Energi dalam bentuk foton cahaya akan
dilepaskan jika elektron berpindah ke lintasan yang
lebih dalam, sedangkan Energi dalam bentuk foton
cahaya akan diserapkan supaya elektron berpindah
ke lintasan yang lebih luar. Energi dilepas atau
diserap dalam paket sebesar hf sesuai dengan
persamaan Planck.
Model Atom Bohr
• lintasan-lintasan stasioner yang diijinkan untuk ditempati
elektron memiliki momentum sudut yang merupakan
kelipatan bulat dari nilai
• Model atom Bohr berhasil menjelaskan kestabilan elektron
dengan memasukkan konsep lintasan atau orbit stasioner
dimana elektron dapat berada di dalam lintasannya tanpa
membebaskan energi. Spektrum garis atomik juga
merupakan efek lain dari model atom Bohr. Spektrum garis
adalah hasil mekanisme elektron di dalam atom yang dapat
berpindah lintasan dengan menyerap atau melepas energi
dalam bentuk foton cahaya. E = hf
• Dengan demikian, struktur atom berdasarkan model
atom Bohr adalah elektron dapat berada di dalam
lintasan-lintasan stasioner dengan energi tertentu.
Lintasan elektron dapat juga dianggap sebagai
tingkat energi elektron.
• Elektron yang berada di lintasan tertentu yang
stasioner dengan jari-jari tertentu dikatakan memiliki
energi tertentu. Elektron yang berada di lintasan ken berada pada jari-jari lintasan dan energi sebagai
berikut
Mengapa Hidrogen tereksitasi?
• Tegangan tinggi pada tabung sinar hidrogen
menyediakan energi tersebut. Molekul hidrogen awalnya
pecah menjadi atom-atom hidrogen (oleh karena itu
disebut spektrum emisi atom hidrogen) dan elektron
kemudian bertransisi ke tingkat energi yang lebih tinggi.
Model atom Hidrogen menurut Bohr
Postulat mengenai Tingkat Energi
Elektron hanya memiliki nilai energi tertentu yang
disebut sebagai tingkat – tingkat energi. Tingkat
energi ini terkuantisasi Untuk elektron dalam atom
H, energi nya dinyatakan dalam :
RH = 2.179 x 10-18 J
n = Bilangan kuantum utama
E
RH
n2
7 | 18
Transisi antar Tingkat Energi
Sebuah elektron bisa memiliki tingkat energi yang
berubah dengan cara mengadsorbsi energi untuk
berpindah ke tingkat energi yang lebih tinggi atau
dengan mengemisikan energi pada saat
berpindah ke tingkat energi yang lebih rendah.
Untuk atom Hidrogen, perubahan tingkat energi
dinyatakan dalam :
ΔE  E f  E i
 1
1
ΔE  RH 

2
n 2
n
i
 f




RH = 2.179 × 10-18 J, Rydberg constant
7 | 19
Energi dari foton yang diadsorbsi atau diemisikan
dinyatakan dalam DE:
E photon  ΔE electron  hn
h  Planck' s constant
Dengan mengkombinasikan dua persamaan di
atas maka diperoleh :
 1

1
hn   R H  2  2 
n

n
i 
 f
7 | 20
Cahaya yang diadsorbsi oleh atom pada saat
transisi elektron dari ni ke nf dimana nf > ni, maka
DE positif.
Cahaya yang diemisikan pada saat elektron
berpindah dari ni ke nf dimana nf < ni , maka DE
negatif
Elektron akan terionisasi pada saat nf = ∞.
7 | 21
Transisi elektron dalam
atom H.
7 | 22
Persamaan Balmer dan Rydberg
• Pada 1885 Balmer memberikan rumus sederhana untuk
memperkirakan panjang gelombang dari beberapa garis yang
sekarang kita kenal dengan deret Balmer.
• Tiga tahun berikutnya, Rydberg membuat rumus yang lebih umum
sehingga dapat diterapkan untuk memperkirakan panjang
gelombang beberapa garis pada spektrum emisi hidrogen.
RH : konstanta Rydberg.
n1 dan n2 merupakan bilangan bulat (seluruh angka).
n2 > n1.
Ada lebih banyak lagi spektrum hidrogen selain tiga
Memperlebar
spektrum
hidrogen
hingga
UV & Hal
IR
garis yang dapat
anda emisi
lihat dengan
mata
telanjang.
ini memunculkan sejumlah "deret" garis yang dinamakan
dengan nama penemunya. Gambar di bawah
menunjukkan tiga dari deret garis tersebut, deret lainnya
berada di daerah infra-merah, jika digambarkan terletak
di sebelah kiri deret Paschen.
• Deret Lyman merupakan deret garis pada daerah ultraviolet. Perhatikan bahwa garis makin merapat satu sama
lain dengan naiknya frekuensi. Akhirnya, garis-garis
makin rapat dan tidak mungkin diamati satu per satu,
terlihat seperti spektrum kontinu. Hal itu tampak sedikit
gelap pada ujung kanan tiap spektrum.
Contoh
Berapa panjang gelombang dari cahaya yang diemisikan oleh
elektron atom H yang bertransisi dari n = 6 to n = 3?
ni = 6
nf = 3
RH = 2.179 × 10-18 J
?E  2.179 x 10
18
 1
ΔE  RH  2 
n
 f
hc
ΔE 
so λ 
λ
1 
ni 2 
hc
ΔE
 1 1 
J)  2  2 = -1.816 x 10-19 J
3 6 

8 m 
6.626 x 10 J s) 2.998 x 10 s 
-6 m
l

1.094
×
10
19
-1.816
x
10
J)

34
7 | 27
Contoh
Sebuah atom memiliki spektrum garis yang
terdiri dari sinar merah dan biru. Asumsikan
masing – masing spektrum tersebut terkait
dengan transisi dua tingkat energi tertentu,
maka gambarkan tingkat energi yang bisa
menjelaskan spektrum terrsebut !
Spektrum Garis
Minimum ada tiga tingkat energi yang diperlukan.
n=3
n=2
n=1
Garis merah terkait dengan transisi dari n = 3 to n
= 2, sedangkan garis biru terkait dengann transisi
dari n = 2 to n = 1.
Copyright © Houghton Mifflin Company. All rights reserved.
7 | 29
Zeeman Effect
Planck
Atom yang bervibrasi memiliki energi sebesar :
E = hn or 2hn or 3hn
Einstein
Energi yang terkuantisasi dari suatu partikel :
E = hn
Bohr
Elektron dalam atom hanya dapat memiliki tingkat energi
tertentu. Untuk atom Hidrogen :
E
RH
n2
RH  2.179 x 10 18 J, n  principal quantum number
7 | 31
Gelombang Partikel
Cahaya memiliki sifat sebagai gelombang dan
partikel, bagaimana dengan partikel ?
7 | 32
Partikel sebagai gelombang
Pada 1923, Louis de Broglie, menyatakan bahwa
partikel bisa berperilaku seperti gelombang.
Panjang gelombang dari partikel yang bermassa m
(kg) dan memiliki kecepatan v (m/s), diberikan oleh
persamaan de Broglie yaitu:
h
λ
mv
 34
h  6.626 x 10 J  s
7 | 33
Contoh
Bandingkan panjang gelombang dari
(a) elektron yang bergerak dengan kecepatan 0.01
kecepatan cahaya (b) bola baseball yang bermassa
0.145 kg dan memiliki kecepatan 26.8 m/s.
Electron
me = 9.11 × 10-31 kg
v = 3.00 × 106 m/s
Baseball
m = 0.145 kg
v = 26.8 m/s
h
λ
mv
7 | 34
Electron
me = 9.11 × 10-31 kg
v = 3.00 × 106
m/s
6.63 x 10 34 J  s
λ
 2.43 × 10-10 m

 31
6 m
9.11 x 10 kg  3.00 x 10

s

Baseball
m = 0.145 kg
v = 26.8 m/s

)
6.63 x 10 34 J  s
λ
 1.71 × 10-34 m
m

0.145 kg ) 26.8 
s

7 | 35
Dengan menggunakan konsep de Broglie’s maka
pada 1926, Erwin Schrödinger mengemukakan
teori untuk menjelaskan sifat gelombang dari
elektron di dalam atom dan molekul (cabang fisika
: Mekanika Kuantum)
7 | 36
Mekanika kuantum menjelaskan bagaima
pergerakan partikel sub atomik tersebut.
Pada1927, Werner Heisenberg menunjukkan
adanya “prinsip ketidakpastian”, bahwa tidak
mungkin kita mengetahui dengan tepat mengenai
posisi, x, dan momentum, p, dari suatu elektron.
h
(Δx )(Δp) 
4π
Karena p = mv maka prinsip ketidakpastian ini
akan signifikan untuk partikel dengan massa <<
7 | 37
Mekanika kuantum menyatakan bahwa posisi
elektron dalam atom tidak dapat ditentukan
dengan pasti, hanya bisa diketahui probabilitasnya
saja.
Dengan
menyelesaikan
persamaan
Schödinger, y,
akan diperoleh informasi
mengenai tingkat – tingkat energi elektron
tersebut. Probabilitasnya dinyatakan dalam y 2
7 | 38
Fungsi gelombang untuk
tingkat energi terendah
dalam atom H.
Probabilitas sangat besar
pada daerah yang dekat
dengan inti
7 | 39
7 | 40
Berdasarkan mekanika kuantum, masing – masing
elektron digambarkan dengan empat bilangan
kuantum:
1.
2.
3.
4.
Bilangan kuantum utama (n)
Bilangan kuantum angular (l)
Bilangan kuantum magnetik (ml)
Bilangan kuantum spin (ms)
Tiga bilangan kuantum pertama di atas
menggambarkan fungsi gelombang elektron,
sedangkan bilangan kuantum ke empat terkait
dengan karakteristik magnetik dari elektron.
7 | 41
Suatu fungsi gelombang elektron dalam atom
menggambarkan daerah atau ruang tertentu
dalam atom dimana probabilitas tertinggi
ditemukan elektron dinyatakan dengan n, l, ml.
7 | 42
Bilangan Kuantum Utama
Bilangan kuantum utama, n
Menggambarkan tingkat energi atau kulit. Semakin
kecil nilai n maka energinya makin rendah dan
orbitnya makin kecil.
n : 1, 2, 3, . . .
Orbit dengan n yang sama dikatakan memiliki kulit
yang sama.
7 | 43
Kulit ( Tingkat Energi)
Kulit biasanya juga dinyatakan dalam simbol :
Letter
n
K
1
L
2
Copyright © Houghton Mifflin Company. All rights reserved.
M
3
N
4
...
7 | 44
Bentuk Orbit
Bilangan kuantum angular, l
Kadang disebut juga sebagai bilangan kuantum
azimuth, menggambarkan orbit – orbit berbeda
yang dimiliki oleh elektron dengan n yang sama.
Bernilai : 0, 1, 2, 3, . . . makssimum (n – 1).
Untuk n tertentu maka ada sejumlah n jenis sub
kulit. Orbit yang memiliki n dan l yang sama akan
berada pada kulit dan sub kulit yang sama.
7 | 45
Bentuk Orbit
Sub kulit dinyatakan dengan huruf kecil yaitu :
n=
l≤
Letter
1
2
3
4
0
s
1
p
2
d
3
f
...
7 | 46
Orientasi Orbit
Bilangan Kuantum Magnetik , ml
Bilangan kuantum ini menyatakan orbit dengan n
dan l bisa memiliki orientasi orbit yang berbeda.
Bilangan kuantum magnetik tergantung pada nilai
l, yaitu berharga : –l sd +l. Setiap nilai l
menggambarkan orbit yang berbeda.
Untuk setiap sub kulit maka ada 2l + 1 orientasi
orbit yang berbeda.
7 | 47
Contoh :
Jika n = 1, l hanya memiliki nilai 0.
Pada l = 0, ml hanya memiliki nilai 0.
Sehingga kulit pertama (n = 1) hanya memiliki satu
sub kulit yaitu subkulit 1s, dan sub kulit tersebut
hanya memiliki satu orientasi orbital
7 | 48
Contoh :
Jika n = 2, l bernilai : 0 and 1.
Pada l = 0, ml memiliki nilai 0, sehingga ada
subkulit 2s dengan satu orbital.
Jika l = 1, ml memiliki nilai -1, 0, 1, sehingga ada
subkulit 2p yang memiliki tiga orientasi orbit
berbeda.
7 | 49
Summary
7 | 50
Kulit dan sub kulit atom Hidrogen
Gambar
disamping
menunjukkan
energi yang
dimiliki
hidrogen pada
kulit dan
subkulit
tertentu
7 | 51
Bilangan kuantum Spin, ms
Bilangan kuantum ini menyatakan dua orientasi
yang mungkin dari elektron.
Bisa bernilai +1/2 or -1/2.
7 | 52
?
Di bawah ini bilangan adalah set
bilangan kuantum, mana yang tidak
diperbolehkan ?
n = 4, l = 4, ml = 0, ms = ½
n = 3, l = 2, ml = 1, ms = -½
n = 2, l = 0, ml = 0, ms = ³/²
n = 5, l = 3, ml = -3, ms = ½
7 | 53
Bentuk dan Ukuran Orbit
Di samping adalah orbit
1s dan 2s dengan
ukuran yang berbeda
7 | 54
Bentuk penampang orbit
1s dan 2s
7 | 55
Bentuk orbit p
7 | 56
Bentuk orbit d
Kompleksitas orbit d bisa dilihat sebagai berikut :
7 | 57