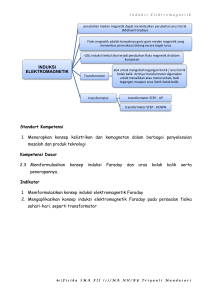
Motor Induksi 3 Phasa dengan Direc Torque Control

Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
1
Pengendali Sliding Mode Control (SMC) Motor Induksi 3
Phasa dengan Direc Torque Control (DTC) Menggunakan
Algoritma Genetika
Oktavianus Kati, Rhiza S. Sadjad, Nadjamuddin Harun
Abstrak
Dalam penelitian thesis ini dikembangkan metode pengaturan
kecepatan motor induksi 3 phasa melalui direct torque control
(DTC) menggunakan sliding mode control (SMC). Dengan
menggunakan metode DTC memungkinkan untuk mengontrol
torka dan fluks stator secara langsung. Estimasi putaran
rotor, torka dan fluks dilakukan oleh DTC yang diberi input
tegangan dan arus stator. Estimasi kecepatan motor akan
dibandingkan dengan kecepatan referensi untuk menghasilkan
error. Error dan delta error kecepatan putar sebagai
masukan pada Sliding Mode Control (SMC), Algoritma
genetika digunakan untuk mencari optimalisasi parameterparameter SMC. Nilai keluaran dari SMC adalah Torka
referensi. Besaran masukan estimasi DTC adalah arus dan
tegangan motor, sinyal masukan inverter adalah tegangan dc.
Besaran keluaran estimasi DTC adalah torka, putaran, fluks
dan sudut antara fluks sumbu d dan sumbu q. Hasil yang
diperoleh melalui simulasi menunjukkan respon kecepatan
putar yang cepat dalam kondisi start, perubahan beban dan
perubahan set point. Khusus pada kondisi perubuhan beban,
respon kecepatan hampir tidak mengalami perubahan
kecepatan atau bisa dikatakan respon kecepatan kokoh bila
ada gangguan
Kata kunci : Sliding mode control, DTC, Algoritma Genetika,
koordinat d-q untuk melakukan analisa. Model d-q lebih
fleksibel dari model trafo, bentuk tegangan sumber
tidak harus sinusoidal dan parameter bisa diubah [1].
Selain itu model d-q dapat menganalisa motor induksi
dalam kondisi : transient, steady state dan perubahan
karena beban. Dalam penelitian ini, pengontrolan
putaran motor induksi dilakukan dengan cara
membandingkan putaran estimasi dengan putaran
referensi. Sinyal tegangan dan arus stator motor induksi
yang telah ditransformasi melalui DTC estimasi
menghasilkan putaran estimasi, fluks, torka estimasi dan
sudut pergesaran. Error antara putaran acuan dengan
putaran estimasi sebagai masukan Sliding mode control
(SMC) dimana parameter dari SMC (h dan beta) kita
optimasi menggunakan algoritma genetika. Output dari
SMC berupa torka referensi dibandingkan dengan torka
estimasi. Hasil perbandingan tersebut berupa sinyal
error yang berfungsi sebagai masukan ke switching
sinyal inverter untuk menyuplai tegangan ke motor
induksi tiga phasa. (gambar 1)
Tujuan dari penelitian ini adalah menerapkan
pengendali SMC sebagai kontrol putaran motor induksi
untuk berbagai kondisi yaitu kondisi start, steady state
dan perubahan setting point perubahan beban motor.

1. Pendahuluan
Motor induksi 3 phasa saat ini banyak digunakan pada
industri dengan berbagai aplikasi. Hal ini disebabkan
karena motor induksi 3 phase memiliki keunggulan
diantaranya handal, tidak ada kontak antara stator dan
rotor kecuali bearing, tenaga yang besar, daya listrik
rendah dan hampir tidak ada perawatan[15]. Motor
induksi 3 phasa memiliki kelemahan pada pengontrolan
kecepatan karena kecepatanya bergantung pada
frekuensi input sedangkan sumber yang ada memiliki
frekuensi yang konstan, untuk mengubah frekuensi
input lebih sulit dari pada mengatur tegangan input,
dengan ditemukannya teknologi inverter maka hal
tersebut menjadi mungkin dilakukan. Motor induksi
umumnya dioperasikan untuk kecepatan tetap.
Berdasarkan survey bahwa bila motor dioperasikan
dengan kecepatan variabel, maka motor akan
mengkonsumsi daya listrik yang kecil. Karena itu motor
ini banyak dipakai dengan kecepatan variabel. Untuk
mengatur kecepatan motor induksi pada kecepatan tetap
dan kecepatan variable diperlukan konverter daya.
Apabila motor induksi mendapat tegangan melalui
konverter daya, maka bentuk gelombang tegangan tidak
lagi sinusoidal. Dalam kondisi ini pemodelan motor
tidak lagi menggunakan model trafo. Pemodelan
dilakukan dengan menggunakan pemodelan dalam
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Vd
ωref
+-
ωerr
Tref
Terr
+-
SMC
ωm
Test
Test ref
+-
 err
Sumber
tegangan
inveter
SVPWM
Tabel
Tegangan
∠𝜽𝒔
str 
est
Vabc
DTC
Estimator
dq
abc
Iabc
Pemodelan d-q
MI
Gambar 1. Blok Diagram sistem pengaturan putaran
motor induksi
2. Model d-q Motor Induksi tiga phasa
Secara konvensional untuk menganalisis motor induksi
tiga phasa dikembangkan berdasarkan model trafo,
dengan mengasumsikan tegangan sumber adalah
sinusoidal dan kondisi steady state. Dalam operasi real
ditemui permasalahan tegangan sumber yang tidak
sinusoidal dan terjadi perubahan beban. Oleh karrna itu
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
dibutuhkan model lain yang lebih fleksibel untuk
menganalisis motor induksi yaitu model motor induksi
dalam koordinat d-q-n. persamaan tegangan motor
induksi dengan tegangan simetri dalam koordinat d-q-n
dinyatakan sbb [7] :
𝑑
𝑣𝑞𝑠 = 𝑅𝑠 𝑖𝑞𝑠 + 𝜔𝜆𝑑𝑠 + 𝜆𝑞𝑠
(1)
𝑣𝑑𝑠 = 𝑅𝑠 𝑖𝑑𝑠 − 𝜔𝜆𝑞𝑠 +
𝑑𝑡
𝑑
𝑑𝑡
𝜆𝑑𝑠
(2)
𝑣𝑞𝑟 = 𝑅𝑟 𝑖𝑞𝑟 + (𝜔𝑔 − 𝜔𝑟 )𝜆𝑑𝑟 +
𝑣𝑑𝑟 = 𝑅𝑟 𝑖𝑑𝑟 − (𝜔𝑔 − 𝜔𝑟 )𝜆𝑞𝑟 +
𝑑
𝑑𝑡
𝑑
𝑑𝑡
𝜆𝑞𝑟
(3)
𝜆𝑑𝑟
(4)
2
𝐾 −1 𝑑𝑞0
𝑐𝑜𝑠𝜃
2𝜋
𝑐𝑜𝑠
(𝜃 − )
=[
𝑐𝑜𝑠 (𝜃 +
3
2𝜋
3
)
−𝑠𝑖𝑛𝜃
1
2𝜋
−𝑠𝑖𝑛 (𝜃 − ) 1]
3
2𝜋
−𝑠𝑖𝑛 (𝜃 + ) 1
(12)
3
Diagram dari model d-q motor induksi tiga phasa dapat
dilihat pada gambar 2 dibawah ini.
Fluksi yang tercakup dalam kumparan adalah :
𝜆𝑞𝑠 = 𝐿𝑙𝑠 𝑖𝑞𝑠 + 𝐿𝑀 (𝑖𝑞𝑠 − 𝑖𝑞𝑟 )
(5)
𝜆𝑑𝑠 = 𝐿𝑙𝑠 𝑖𝑑𝑠 + 𝐿𝑀 (𝑖𝑑𝑠 + 𝑖𝑑𝑟 )
(6)
𝜆𝑞𝑟 = 𝐿𝑙𝑟 𝑖𝑞𝑟 + 𝐿𝑀 (𝑖𝑞𝑠 + 𝑖𝑞𝑟 )
(7)
𝜆𝑑𝑟 = 𝐿𝑙𝑟 𝑖𝑑𝑟 + 𝐿𝑀 (𝑖𝑑𝑠 + 𝑖𝑑𝑟 )
(8)
Torka elektromagnetik motor induksi dapat ditentukan
dengan:
3 𝑷
𝑇𝑒 = ( ) (𝜆𝑑𝑠 𝑖𝑞𝑠 − 𝜆𝑞𝑠 𝑖𝑑𝑠 )
(9)
2 2
Dan persamaan dinamis dari motor induksi dinyatakan
oleh :
𝑇𝑒 − 𝐵𝑚 𝜔𝑟 − 𝑇𝐿 =
𝑑
2𝐽 𝑑𝜔𝑟
= 𝜔𝑟 (𝑡)
Dimana :
𝑇𝐿 : torka beban
𝑇𝑒 : torka elektromagnetik
J
: momen inersia (kg.m2)
P
: jumlah kutub
𝜔𝑟 : kecepatan angular rotor (rad/detik)
𝐵𝑚 : koefisien gesekan (N.m.det/rad)
𝜃𝑟 : posisi sudut (rad)
(11)
Persamaan (1 s/d 11) dapat dinyatakan dalam bentuk
matriks menjadi :
𝜔𝐿𝑠
𝑅𝑠 + 𝑝𝐿𝑠
(𝜔𝑔 − 𝜔𝑟 )𝐿𝑀
𝑝𝐿𝑀
−𝜔𝐿𝑀
𝑅𝑟 + 𝑝𝐿𝑟
𝑝𝐿𝑀
(𝜔𝑔 − 𝜔𝑟 )𝐿𝑟
𝜔𝐿𝑀
𝑖𝑞𝑠
𝑝𝐿𝑀
𝑖𝑑𝑠
[
(𝜔𝑔 − 𝜔𝑟 )𝐿𝑟 𝑖𝑞𝑟 ]
𝑅𝑟 + 𝑝𝐿𝑟 ] 𝑖𝑑𝑟
Untuk lebih memudahkan dalam menghitung arus dan
tegangan dalam bentuk d-q dan sebaliknya kita dapat
menggunakan transformasi matriks kombinasi ClarkePark yakni:
𝐾𝑑𝑞0 =
2
3
[
2𝜋
−𝑠𝑖𝑛𝜃
−𝑠𝑖𝑛 (𝜃 −
)
3
2𝜋
3
𝑐𝑜𝑠 (𝜃 +
2𝜋
) −𝑠𝑖𝑛 (𝜃 +
1
1
1
2
2
2
Dari model matematika diatas, persamaan-persamaan
tersebut dapat disederhanakan untuk memperoleh
persamaan keadaa (state space) yang kemudian
digambarkan dalam bentuk vector matriks persamaan
keadaan. Selanjutnya dari persamaan keadaan akan
didapatkan diagram keadaan yang akan membantu kita
dalam menentukan diagram blok sistem nantinya.
Pertama persamaan yang harus diuraikan adalah
persamaan tegangan acuan masukan (1) dan (4):
𝑑
𝑖 (𝑡)
𝑑𝑡 𝑑𝑠
𝑑
𝑖 (𝑡)
𝑑𝑡 𝑞𝑠
𝑑
𝑑𝑡
𝑑
1
𝑉 (𝑡)
𝜎𝐿𝑠 𝑑𝑠
1
+
𝑉 (𝑡)
𝜎𝐿 𝑞𝑠
= 𝛽𝑛𝑝 𝜔𝑚 (𝑡)𝜆𝑞𝑟 + 𝜂𝛽𝜆𝑑𝑟 + 𝛾𝑖𝑑𝑠 (𝑡) +
= −𝛽𝑛𝑝 𝜔𝑚 (𝑡)𝜆𝑑𝑟 + 𝜂𝛽𝜆𝑞𝑟 − 𝛾𝑖𝑞𝑠 (𝑡)
𝑠
(13)
(14)
𝑖𝑑𝑟 (𝑡) = −𝑛𝑝 𝜔𝑚 (𝑡)𝜆𝑞𝑟 − 𝜂𝜆𝑑𝑟 + 𝜂𝐿𝑚 𝑖𝑑𝑟 (𝑡)
(15)
𝑖𝑞𝑟 (𝑡) = 𝑛𝑝 𝜔𝑚 (𝑡)𝜆𝑑𝑟 − 𝜂𝜆𝑞𝑟 + 𝜂𝐿𝑚 𝑖𝑞𝑟 (𝑡)
(16)
Dari persamaan (9) dan (11) kita dapatkan :
Dimana Ls dan Lr adalah induktansi sendiri untuk stator
dan rotor dan Lm adalah induktansi bersama antara
stator dan rotor.
𝑐𝑜𝑠 (𝜃 −
Persamaan Ruang Keadaan dan Diagram
Keadaan Motor Induksi
𝑑𝑡
Dengan 𝐿𝑠 = 𝐿𝑙𝑠 + 𝐿𝑀 dan 𝐿𝑟 = 𝐿𝑙𝑟 + 𝐿𝑀
𝑐𝑜𝑠𝜃
Sumber : Toh Chuen Ling, Implementation of DTC of
Induction Machines, UTM, 2005
(10)
𝑃 𝑑𝑡
𝜃 (𝑡)
𝑑𝑡 𝑟
𝑅𝑠 + 𝑝𝐿𝑠
𝑉𝑞𝑠
−𝜔𝐿𝑠
𝑉𝑑𝑠
=
𝑝𝐿𝑀
𝑉𝑞𝑟
[𝑉𝑑𝑟 ] [−(𝜔𝑔 − 𝜔𝑟 )𝐿𝑀
Gambar 2. Rangkaian ekivalen d-q dinamik motor
induksi (a) rangkaian d-axis, (b) rangkaian q-axis
3
𝜔𝑚 (𝑡) = 𝑛𝑝
𝐿𝑚 (𝜆𝑑𝑟 𝑖𝑞𝑠 (𝑡)−𝜆𝑞𝑟 𝑖𝑑𝑠 (𝑡))
𝐿𝑟 𝐽
−
𝐵𝑚
𝐽
𝜔𝑚 (𝑡) −
𝑇𝐿 (𝑡)
𝐽
(17)
Dimana :
𝑅𝑟
𝐿2𝑚
𝐿𝑚
𝜂=
; 𝜎 =1−
; 𝛽=
𝐿𝑟
𝐿𝑟 𝐿𝑠
𝜎𝐿𝑟 𝐿𝑠
𝐿
𝑅
𝐿
𝛾 = 𝑚 2 + 𝑠 dan 𝜇 = 𝑛𝑝 𝑚
𝜎𝐿𝑎 𝐿𝑟
𝜎𝐿𝑠
𝐽𝐿𝑟
Dari persamaan diatas kita dapatkan vector matriks
persamaan ruang keadaan (state space) berikut ini :
)
3
2𝜋
𝑑
𝑑𝑡
(11)
)
]
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
d

 .n p . m
 dt isd (t )   

 
 d i (t )  -  .n p . m -.
 dt sq    
- n p . m

 
 d rd (t )  n p . m -
 dt
 =
d
 
 rq (t )   .isq (t ) - .isd (t )
dt

 
0
d
  0
 m (t ) 
dt


d

  m (t ) 
 dt


0

0

0
0

0
0
0

0

0
1 / J

0
0
0
-
0
Lm
0
0
0
0
0
0
0
0
0
0
0
0
0
Lm 0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
B
- m
J
1
0

0
0

0

0 

0
Untuk mendapatkan fungsi alihnya, maka kita
membandingkan antara 𝜔𝑚 (𝑡) sebagai keluaran dan
𝑉𝑑𝑠 (𝑡) dan 𝑉𝑞𝑠 (𝑡)sebagai masukan dua koordinat
orthogonal dan polar, direct-quadrature (d-q). untuk
mendapatkan fungsi alih, maka salah satu dari tegangan
acuan masukan dan 𝑇𝐿 (𝑡) harus sama dengan nol. Dari
Persamaan (10) diatas :
(𝐽𝑠 + 𝐵𝑚 )𝜔𝑚 (𝑡) = 𝑇𝑒𝑚 (𝑡) − 𝑇𝐿 (𝑡)
 r 




rq 





. 0 




0 






 m (t )
𝑇
(𝑠)
𝑒𝑚
𝜔𝑚 (𝑠) = (𝐽𝑠+𝐵
𝑚)
0
0
0
x
0
0

0 
Untuk memudahkan memperoleh diagram keadaan dan
diagram blok dari persamaan diatas maka perlu
penyederhanaan terhadap matriks pers. (18) diatas,
dengan mengambil bagian yang dianggap perlu
dideskripsikan :
-
0
d
  Lm  Rs 0
 dt isd (t )    .Ls .Lr 2  .Ls

 
Lm
R
 d i (t )   0
- s
2
 dt sq  

.Ls

.
L
.
L
s r

 
 d rq (t ) 
0
0
 dt
 
0  isd (t )  Vsd (t )
 

 
 
 1
 


  x isq (t )  Vsq (t ) .



  .Ls

 

 

-   rq (t ) 0




 isd (t )  Vsd (t )
 

 

 
 1
Rr Lm  


x isq (t )  Vsq (t ) .
2
 
  .Ls
 .Ls .Lr  

 

Rr  


  (t ) 0 
Ls   rq  
0
𝑛𝑝 𝐿𝑚 (𝜆𝑑𝑟 𝑖𝑞𝑠 (𝑠)−𝜆𝑞𝑟 𝑖𝑑𝑠 (𝑠))
(21)
𝐿𝑟 (𝐽𝑠+𝐵𝑚 )
𝑅𝑟
𝐿𝑚
𝐿𝑚
𝑅𝑠
𝜆 )
+(
+
) 𝑖 (𝑡)
𝐿𝑟 𝑑𝑟 𝜎𝐿𝑠 𝐿𝑟
𝜎𝐿𝑠 𝐿2𝑟 𝜎𝐿𝑠 𝑑𝑠
𝑑
+ 𝑖𝑑𝑠 (𝑡)𝜎𝐿𝑠
𝑑𝑡
𝐿𝑚
𝑅𝑟 𝐿𝑚
𝐿𝑚
𝑉𝑑𝑠 (𝑡) = 𝑛𝑝
𝜔 (𝑠)𝜆𝑞𝑟 + 2 𝜆𝑑𝑟 + ( + 𝑅𝑠 + 𝜎𝐿𝑠 𝑠) 𝑖𝑑𝑠 (𝑠)
𝐿𝑟 𝑚
𝐿𝑟
𝐿𝑟
𝑉𝑑𝑠 (𝑡) = (𝑛𝑝 𝜔𝑚 (𝑡)𝜆𝑞𝑟 +
(18)
0
=
Dari persamaan (13):
𝑉𝑑𝑠 (𝑡) = 𝑛𝑝 𝛽𝜔𝑚 (𝑡)𝜆𝑞𝑟 + 𝜂𝛽𝜆𝑑𝑟 + 𝛾𝑖𝑑𝑠 (𝑡)𝜎𝐿𝑠
Jika 𝛽, 𝜂 dan 𝛾 disubtitusikan :
isd (t ) Vsd (t )
i (t )  V (t )  1
 sq   sq 
  .Ls
ird (t ) 0


+ 
0
i
(
t
)

 rq  


 0

0  

0  0

 . TL (t )







d
 
 dt isd (t )  

 
 d i (t )   0
 dt sq  

 
 d rq (t ) 
 dt
 0
3
(19)
Maka persamaan persamaan fungsi alih motor induksi
adalah :
𝑛𝑝 𝐿𝑚 (𝜆𝑑𝑟 𝑖𝑞𝑠 (𝑠) − 𝜆𝑞𝑟 𝑖𝑑𝑠 (𝑠))
𝜔𝑚 (𝑠)
𝐿𝑟 (𝐽𝑠 + 𝐵𝑚 )
=
𝑉𝑑𝑠 (𝑠) 𝑛 𝐿𝑚 𝜔 (𝑠)𝜆 + 𝑅𝑟 𝐿𝑚 𝜆 + (𝐿𝑚 + 𝑅 + 𝜎𝐿 𝑠) 𝑖 (𝑠)
𝑝 𝐿
𝑚
𝑞𝑟
𝑠
𝑠
𝑑𝑠
𝐿𝑟
𝐿2𝑟 𝑑𝑟
𝑟
(22)
𝑛𝑝 𝐿𝑚 (𝜆𝑑𝑟 𝑖𝑞𝑠 (𝑠) − 𝜆𝑞𝑟 𝑖𝑑𝑠 (𝑠))
𝐿𝑟
=
𝑛𝑝2 𝐿2𝑚
𝐿
𝑅
𝐿
𝑚
𝑟
𝐽𝜎𝐿𝑠 𝑠 2𝑖𝑑𝑠 (𝑠) + ((𝑅𝑠 + 2 ) 𝑖𝑑𝑠 (𝑠) + 2 𝑚 𝜆𝑑𝑟 ) 𝐽𝑠 + 2 (𝜆𝑑𝑟 𝑖𝑞𝑠 (𝑠) − 𝜆𝑞𝑟 𝑖𝑑𝑠 (𝑠))
𝐿𝑟
𝐿𝑟
𝐿𝑟
Diperoleh diagram blok motor induksi :
(20)
Sehingga dari vektor matriks diatas didapatkan diagram
keaadan motor induksi :
Gambar 4. Diagram blok Motor Induksi
dq --> abc
d
ia
1
q
ib
ia
2
ic
ib
3
Demux
abc --> dq
sumber 3 fasa
[theta_da]
Va
theta_da
ic
Vb
vs_dq
-K-
vs_dq
Vc
Va,Vb,Vc=380 volt
f=50 hz
theta_da
f l_rd
lambda --> i
inv[M]
is_dq fl_s_dq
1
s
is_dq
-KDemux
f l_rd
Demux
K*u
irdq
theta_da
1
s
[theta_da]
Wd
0
Pers. stator_flux
-KTerminator
fl_rq
1
s
WdA=s*Wd
f l_rd
Scope2
Wm
p/2
Wmech
Inertia
-K-
Torque
-Kxo
Torsi
1
s
Put_Motor
To Workspace
Wmech_0
Scope1
Gambar 5. Model Simulasi Motor Induksi
Gambar 3. Diagram Keadaan Motor Induksi
Sumber : Liu-Kong-Chao, Speed Estimation of Induction
Motor Using Non Linear Identification Technique, 1999
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Model simulasi motor induksi seperti pada gambar (5)
diatas di verifikasi dengan memberikan input suplai
tegangan 3 fasa (380 volt), respon kecepatan putar
motor seperti pada gambar (6) :
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
2
𝜆𝑠 = √(𝜆𝑞𝑠 ) + (𝜆𝑑𝑠 )2 ∠𝜃𝑠
Grafik Verifikasi model motor induksi
160
𝜃𝑠 = tan−1 (
140
120
Putaran [ra/detik]
4
𝜆𝑞𝑠
𝜆𝑑𝑠
(8)
)
(9)
Frekuensi listrik dihitung dengan mendiffrensialkan
sudut vector fluks rotor yaitu :
100
80
𝜃𝑟 = 𝑡𝑎𝑛−1 (
60
40
20
0
𝜆𝑞𝑠
𝜆𝑑𝑠
)
(10)
Persamaan turunan dari (10) adalah :
𝜆 𝜆̇ −𝜆 𝜆̇
𝜃̇𝑟 = 𝜔𝑒 = 𝑑𝑠 𝑞𝑠 2 𝑞𝑠 𝑑𝑠
(11)
Dan persamaan kecepatan rotornya adalah :
𝑇
𝜔𝑟 = 𝑃 (𝜔𝑒 − 𝑅𝑟 𝑒2)
(12)
𝜆𝑠
-20
0
1
3
2
4
5
6
8
7
time[detik]
𝜆𝑟
Gambar 6. Respon Motor induksi Tanpa DTC
Fluks Stator
Dari gambar (6) kita lihat bahwa motor masih
mengalami goncangan-goncangan pada saat start awal
dan waktu yang dibutuhkan untuk mencapai kondisi
putaran steady-state cukup lama (tss=2,248 detik,
𝜔=156,4 rad/detik).
1
v_abc
Zero-Order
Hold1
0 = 𝑅𝑟 𝑖̅𝑟 +
− 𝑗𝜔𝑟 𝜆̅𝑟
(2)
𝑑𝑡
′
𝜆̅𝑠 = 𝐿𝑠 𝑖̅𝑠 + 𝐿𝑚 𝑖̅𝑟
(3)
𝜆̅𝑟 = 𝐿𝑟 𝑖̅𝑟 + 𝐿𝑚 𝑖̅𝑠
(4)
Sehingga :
𝜆̅𝑠 = ∫(𝑣̅𝑠 − 𝑅𝑠 𝑖̅𝑠 )𝑑𝑡
(5)
Dengan demikian fluks lingkages dalam koordinat
stator reference frame dihitung berdasarkan
𝜆̅𝑞𝑠 = ∫(𝑣̅𝑞𝑠 − 𝑅𝑠 𝑖̅𝑞𝑠 )𝑑𝑡
(6)
̅
𝜆𝑑𝑠 = ∫(𝑣̅𝑑𝑠 − 𝑅𝑠 𝑖̅𝑑𝑠 )𝑑𝑡
(7)
Sehingga besarnya fluks stator adalah
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
fl_s_est
ang_fl_s
atan2(u(2),u(1))
2
abc alfabeta
f(u)
f l_r_ab
-K-
2
ang_f l_ssector
Sector
Tem
3
Tem_est
Lr/Lm
Rs
f(u)
f l_r_ab
Zero-Order
Hold2
-K-
f l_r^2
atan2(u(2),u(1))
-K-
Wslip_elec
Wm_est
theta_rW r_elec
4
(2/p)
Wmech_est
Zero-Order
Hold3
Gambar 7. Blok diagram DTC
Respon putaran motor terhadap kecepatan referensi dan
perubahan beban dengan Direct Torque Control seperti pada
gambar (8), terlihat bahwa kecepatan putaran motor akan
mengikuti putaran referensi motor yang telah disetting
(𝜔𝑟𝑒𝑓 =68,57 rad/detik), tampak bahwa waktu yang diperlukan
untuk mencapai keadaan steady state cukup cepat dibanding
respon motor tanpa DTC (tss = 0,1674 detik), adanya
perubahan beban (torsi) sebesar 17,57 N.m menyebabkan
putaran motor akan turun menjadi 51,3 rad/detik atau sebesar
25,43% dari kecepatan motor yang kita inginkan (kecepatan
referensi).
Respon Putaran MOTOR terhadap beban dengan DTC
80
Putaran (rad/det) atau Torsi Beban (N.m)
70
60
50
40
Kec.Motor.Aktual (rad/det)
Kec.Motor ref.(rad/det)
Torsi(N.m)
30
20
10
0
-10
(1)
1
f l_s
Ls*sigma
Direct Torque Control pertama kali dikembangkan oleh
Takahasi dan Noguchi tahun 1986. Dasar dari metode
DTC adalah perubahan torsi sebanding dengan slip
antara fluks stator dan fluks rotor pada kondisi fluks
bocor stator tetap [4]. Pada motor induksi dengan tipe
rotor sangkar untuk waktu tetap rotor menjadi sangat
besar, fluks bocor berubah perlahan dibanding dengan
perubahan fluks bocor stator. Oleh karena itu pada
keadaan perubahan cepat fluks rotor cenderung tidak
berubah. Perubahan cepat dari torsi elektromagnetik
dapat dihasilkan dari putaran fluks stator, sebagai arah
torsi. Dengan kata lain fluks stator dapat seketika
mempercepat atau memperlambat dengan menggunakn
vektor tegangan stator yang sesuai. Torsi dan fluks
kontrol bersama-sama dan decouple dicapai dengan
pengaturan langsung dari tegangan stator, dari error
respon torsi dan fluks. DTC biasanya digunakan sesuai
vector tegangan dalam hal ini untuk memelihara torsi
dan fluks stator dengan dua daerah histerisis. Untuk
menentukan putaran motor dapat digunakan persamaan
rangkaian dan arus motor diukur pada reference frame
yang dapat dipilih dalam stator frame, persamaan
tegangan stator dalam kerangka stator referensi
diberikan [1] dengan persamaan :
𝑑𝑡
̅𝑟
𝑑𝜆
f(u)
Discrete-Time
Integrator
3. Direct Torque Control (DTC)
̅𝑠
𝑑𝜆
f l_s_ab
z-1
angle to sector no.
i_abc
𝑣̅𝑠 = 𝑅𝑠 𝑖̅𝑠 +
K Ts
abc alfabeta
0
0.5
1
1.5
2
2.5
3
time[detik]
Gambar 8. Respon Motor terhadap kecepatn referensi
dan perubahan beban dengan DTC
4. Space Vektor PWM
Space vector modulation (SVM) adalah teknik modulasi
yang dikembangkan melalui space vector (vector ruang)
yang akan menjadi tegangan acuan dengan periode
sampling tertentu ke inverter, dengan menggunakan dua
tegangan acuan yaitu Vd dan Vq dan sudut. Teknik
SVPWM dapat digunakan untuk membangkitkan pola
switching inverter 3 phasa jenis sumber tegangan (VSI).
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
5
Bila tegangan acuan 3 phasa diberikan dalam bentuk
Va, Vb dan Vc maka diperlukan transformasi dari 3
phasa ke 2 phasa. Space vector dengan persamaan 3
phasa dapat dinyatakan Va(t), Vb(t) dan Vc(t) yang
masing-masing mempunyai pergeseran phasa sebesar
120 derajat. Persamaan dalam vektor dapat dinyatakan
sebagai berikut[3] :
2
𝑉̅ (𝑡) = (𝑉𝑎 (𝑡) + 𝑉𝑏 (𝑡)𝑎 + 𝑉𝑐 (𝑡)𝑎2 )
(1)
3
Dimana :
2𝜋
2𝜋
Sector 2
V010
V110
Sector 1
Sector 3
Vref
tb
V000
V011
V100
ta
V111
Sector 4
Sector 6
2𝜋
𝑎 = 𝑒 𝑗 3 = 𝑐𝑜𝑠 ( ) + 𝑗𝑠𝑖𝑛 ( ) = 0,5 + 𝑗0,8667
4𝜋
3
4𝜋
3
4𝜋
3
3
V001
𝑎2 = 𝑒 𝑗 3 = 𝑐𝑜𝑠 ( ) + 𝑗𝑠𝑖𝑛 ( ) = −0,5 − 𝑗0,8667
V101
Sector 5
Persamaan ini juga berlaku untuk arus dan fluks.
Gambar 10. Space vector voltage
5. Sliding Mode Control (SMC)
Sumber teg.
D1 D3 D5
tiga phasa
a
b
c
D4 D6 D2
T1
T
R
RR
Cf
T3
a
T4
Dioda Bridge Regenerating Link
Rectifier
Circuit
Filter
T5
b
c
T6
MI
T2
PWM Inverter
Gambar 9. Rangkaian Daya penggerak Motor Induksi
tiga phasa
Pada inverter tiga phasa (gambar 9) dapat dibuat
beberapa kombinasi switching yang akan menghasilkan
vector tegangan yang berbeda. Jika T 1 on dan T4 off
(dilambangkan dengan Sa=1) maka pada Va timbul
tegangan sebesar Vdc. Demikain juga halnya pada Sb
dan Sc. Ada 8 jenis switching yang berbeda yang dapat
dibuat dari kombinasi Sa, Sb dan Sc seperti kita lihat
pada tabel 1.
Vektor tegangan yang terjadi untuk tegangan line to line
berlaku :
𝑣𝑎𝑏 = 𝑣𝑎 − 𝑣𝑏
𝑣𝑏𝑐 = 𝑣𝑏 − 𝑣𝑐 }
(2)
𝑣𝑐𝑎 = 𝑣𝑐 − 𝑣𝑎
Sehingga output tegangan inverter dapat ditentukan
dengan menggunakan persamaan matriks berikut:
𝑉𝑎
2 −1 −1 𝑎
1
[𝑉𝑏 ] = 𝑉𝑑𝑐 [−1 2 −1] [𝑏 ]
(3)
3
𝑉𝑐
−1 −1 2 𝑐
Tabel 1. Kondisi switching inverter
Sector
On Device
Va
Vb
Vc
0
0
0
2/3𝑣𝑑𝑐
−1/3𝑣𝑑𝑐 −1/3𝑣𝑑𝑐
1/3𝑣𝑑𝑐
1/3𝑣𝑑𝑐
−2/3𝑣𝑑𝑐
−1/3𝑣𝑑𝑐
2/3𝑣𝑑𝑐
−1/3𝑣𝑑𝑐
−2/3𝑣𝑑𝑐 1/3𝑣𝑑𝑐
1/3𝑣𝑑𝑐
−1/3𝑣𝑑𝑐
−1/3𝑣𝑑𝑐
2/3𝑣𝑑𝑐
Space Voltage
Vector
0
1
2
3
4
5
T2,T4,T6
T1,T4,T6
T1,T3,T6
T3,T2,T6
T2,T3,T5
T2,T4,T5
6
T1,T4,T5
1/3𝑣𝑑𝑐
−2/3𝑣𝑑𝑐
1/3𝑣𝑑𝑐
V6(101)
7
T1,T3,T5
0
0
0
V7(111)
V0(000)
V1(100)
V2(110)
V3(010)
V4(011)
V5(001)
Untuk meningkatkan performa putaran motor induksi 3
phasa pada kondisi ada gangguan, maka kontrol putaran
menggunakan Sliding mode control (SMC). Jenis
control SMC sangat kokoh (robust) pada saat terjadi
gangguan dengan variasi parameter dan torka beban
berubah. Pada gambar 1 ditunjukkan blok diagram
sistem yang dimaksud. Persamaan umum torka
elektromekanik pada motor induksi adalah [11] :
𝐽
𝑑𝜔𝑚
𝑑𝑡
+ 𝐵𝜔𝑚 + 𝑇𝐿 = 𝑇𝑒
(1)
dimana : J dan B adalah konstanta inersia dan koefisien
gesekan dari motor. TL adalah torka beban dan ωm
adalah putaran sudut mekanik rotor. T e adalah torka
elektromagnetik motor induksi dengan persamaan :
𝑃
𝑇𝑒 = 1,5 (𝜆𝑑𝑠 𝑖𝑞𝑠 − 𝜆𝑞𝑠 𝑖𝑑𝑠 )
2
Persamaan elektromekanik (1) dapat diubah menjadi:
𝐵
𝑇𝐿
𝐽
𝐽
𝜔̇ 𝑚 + 𝜔𝑚 +
apabila 𝑎 =
𝐵
𝐽
1
= 𝑇𝑒
(3)
𝐽
1
𝑇𝐿
𝐽
𝐽
;𝑏 = ;𝑑 =
maka persamaan (3)
diatas jika kondisi gangguan persamaannya menjadi :
𝜔̇ 𝑚 = −(𝑎 + Δ𝑎)𝜔𝑚 − (𝑑 + Δ𝑑) + (𝑏 + Δ𝑏)𝑇𝑒 (4)
Δ𝑎, Δ𝑏 dan Δ𝑑 adalah kondisi taktentu dari parameter a,
b dan d sebagai pernyataan parameter J dan B. Untuk
menentukan error putaran motor digunakan persamaan:
∗
𝑒(𝑡) = 𝜔𝑚 (𝑡) − 𝜔𝑚
(𝑡)
(5)
∗
dengan 𝜔𝑚 (𝑡) adalah putaran acuan (referensi). Jika
kita differensialkan persamaan (5) kita dapatkan
persamaan :
∗ (𝑡) = −𝑎𝑒(𝑡) + 𝑓(𝑡) + 𝑥(𝑡) (6)
𝑒̇ (𝑡) = 𝜔̇ 𝑚 (𝑡) − 𝜔̇ 𝑚
Dengan memisahkan komponen 𝑓(𝑡) dan 𝑥(𝑡) dari
persamaan (6) kita peroleh :
∗
∗
𝑓(𝑡) = 𝑏𝑇𝑒 (𝑡) − 𝑎𝜔𝑚
− 𝑑(𝑡) − 𝜔̇ 𝑚
(7)
𝑥(𝑡) merupakan perubahan yang terjadi dan diberikan
dalam persamaan :
∗
𝑥(𝑡) = 𝑏𝑇𝑒 (𝑡) − Δ𝑎𝜔𝑚
− Δ𝑑(𝑡) − Δ𝑏𝑇𝑒 (𝑡) (8)
Variable silidng mode control dengan komponen
integral diberikan dalam persamaan :
𝑡
𝑆(𝑡) = 𝑒(𝑡) − ∫0 (ℎ − 𝑎)𝑒(𝜏)𝑑𝜏
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
(2)
(9)
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
Dimana h menyatakan konstanta penguat. Untuk
menentukan alur putaran (speed trajectory tracking),
digunakan asumsi dan persamaan berikut :
Asumsi 1 : harga h dipilih sehingga (h-a) menjadi
positip dan h>0, kemudian sliding surface diberikan
dengan persamaan:
𝑡
𝑆(𝑡) = 𝑒(𝑡) − ∫0 (ℎ − 𝑎)𝑒(𝜏)𝑑𝜏 = 0
(10)
Agar control switching dijamin berada di sliding mode,
maka kontrol putarannya diberikan dengan persamaan :
𝑓(𝑡) = ℎ𝑒(𝑡) − 𝛽𝑠𝑔𝑛(𝑆(𝑡))
(11)
𝛽 merupakan konstanta penguat switch . S(t) adalah
variable sliding yang ditentukan melalui persamaan (8)
dan sgn(.) adalah fungsi signum yang didifinisikan
sebagai berikut :
+1 𝑏𝑖𝑙𝑎 𝑆(𝑡) > 0
𝑠𝑔𝑛(𝑆(𝑡)) = {
(12)
−1 𝑏𝑖𝑙𝑎 𝑆(𝑡) < 0
Asumsi 2. Penguat 𝛽 dipilih sehingga 𝛽 ≥ |𝑥(𝑡)| untuk
semua kondisi. Ketika sliding mode terjadi pada sliding
surface persamaan (9), 𝑆(𝑡) = 𝑆̇(𝑡) = 0, dan tracking
error 𝑒(𝑡) bergerak konvergen secara eksponen menuju
𝒙̇
nol.
trayektori
chattering
x
xd(t)
Surface
sliding
S=0
Gambar 11. Diagram fasa trayektori status
Sumber : Slotine and Li, 1991
Sesuai dengan parameter motor induksi dari persamaan
(4), bila asumsi 1 dan asumsi 2 dibuktikan sebagai
batasan putaran persamaan (11) akan mendahului
putaran mekanik 𝜔𝑚 sehingga tracking kesalahan
∗
putaran 𝑒(𝑡) = 𝜔𝑚 (𝑡) − 𝜔̇ 𝑚
(𝑡) cenderung menuju
ketitik nol sehingga menuju kondisi tak berhingga.
Pembuktian dari teorema diatas dapat menggunakan
teori stabilitas Lyapunov. Fungsi Lyapunov adalah[12]
1
𝑉(𝑡) = 𝑆(𝑡)𝑆(𝑡)
2
(13)
̇
𝑉̇ (𝑡) = 𝑆(𝑡)𝑆(𝑡)
(14)
Dengan menggunakan persamaan (14) maka kita
dapatkan :
̇
𝑉̇ (𝑡) = 𝑆(𝑡)𝑆(𝑡)
= 𝑆[𝑒̇ − (ℎ − 𝑎)𝑒]
= 𝑆[(−𝑎𝑒 + 𝑓 + 𝑥) − (ℎ𝑒 − 𝑎𝑒)]`
= 𝑆[𝑓 + 𝑥 − ℎ𝑒]
= 𝑆[ℎ𝑒 − 𝛽𝑠𝑔𝑛(𝑆(𝑡)) + 𝑥 − ℎ𝑒]
6
Selanjutnya untuk menentukan nilai 𝛽 (beta) dan h
digunakan metode optimasi Algoritma Genetika. GA
diharapkan dapat menyesuaikan nilai 𝛽 dan h agar error
menuju nilai konvergen pada setiap ada perubahan.
Akhirnya torka referensi 𝑇𝑒∗ dapat ditentukan dengan
mensubtitusikan persamaan (7) ke persamaan (11), kita
peroleh :
1
∗ + 𝜔̇ ∗ + 𝑑] (13)
𝑇𝑒∗ = [ℎ𝑒(𝑡) − 𝛽𝑠𝑔𝑛(𝑆(𝑡)) + 𝑎𝜔𝑚
𝑚
𝑏
1
e(t)
Delta Wem*
2
Beta
Beta
3
Tem*
Out1
1
Tem*
Zero-Order
Hold
h
h
SMC
Gambar 12. Diagram simulink SMC
6. Hasil Simulasi
Hasil yang diperoleh secara simulasi dengan
menggunakan simulink/Matlab dengan data sebagai
berikut : sampling time 100s, fluks referensi diambil
pada harga nominal. Data lengkap parameter motor
induksi dapat dilihat pada tabel 2 dibawah ini :
Tabel 2. Parameter-paramter Motor induksi
Daya
7,5
HP/kW
5,6
kW
Tegangan, V
380
Volt(LL,rms)
Fasa (F)
3
phasa
Tahanan Stator, Rs
1,77
Ohm
Tahanan Rotor, Rr
1,34
Ohm
Reaktansi Stator, Xs
5,25
Ohm
Reaktansi Rotor, Xr
4,57
Ohm
Reaktansi Gandeng, Xm
1,39
Ohm
Momen Inersia Motor, J
0.025 Kg.m2
Jumlah kutub, P
4
buah
Frekuensi,f
50
Hertz
Slip, S
3
Persen
Koefisien gesek,B
0.01
N.m.sec/rad
Arus beban Penuh, I
4
Ampere
Slip beban penuh (s)
1,72
Ohm
Sumber : Arman Jaya, “Pengaturan kecepatan motor induksi tanpa
sensor
tegangan stator
Delta Wem*
kec motor referensi
Beta
Tem*
h
volt
Delta Tem*
qa va
va
ia
-3.547
Delta Flux
Demux qb vb
vb
ib
volt1
3.271
qc vc
vc
ic
Switch signal
Sliding Mode Control
Sector
fl_s_0
Drive signal
Demux
0.2762
Torsi beban Wmech
Inverter
Flux_referensi
ia
ib arus stator
ic
ampere
Motor Induksi
fl_s_est
h
Arus Stator
v_abc
76.2
Sector
Beta
Demux
Tem_est
Algoritma Genetika
i_abc
76.18
0
Va
Torsi Beban
1
1/s
time
Integrator
Waktu
TIMER
Wmotor ref.
Torsi beban
N.m
DTC Estimator
Constant
Wmotor
rad/detik
Wmech_est
Demux
Vb
Vc
Putaran rotor
Wmotor
Wmotorref
workspace tegangan
Torsi
Ia
workspace
Demux
Ib
Ic
workspace Arus
= 𝑆[𝑥 − 𝛽𝑠𝑔𝑛(𝑆(𝑡))]
Sehingga 𝛽𝑠𝑔𝑛(𝑆(𝑡)) ≤ 0
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Gambar 13. Diagram Sistem Simulasi SMC Motor
Induksi
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
Gambar 14 : merupakan respon putaran motor saat
start, perubahan referensi kecepatan dan perubahan
beban, Over-shoot yang dihasilkan pada saat start,
perubahan referensi kecepatan dan perubahan beban
serta waktu yang dibutuhkan untuk mencapai kondisi
steady state dapat dilihat pada table berikut :
Tabel 3. Respon Putaran Motor
Parameter terukur
Kondisi
Overshoot
(iss)
Start
Perubahan referensi kecepatan
Perubahan beban (torsi)
9,43 rad/det
15,74 rad/det.
4,85 rad/det.
Respon Putaran MOTOR terhadap Perubahan Torsi Beban dan Perubahan Referensi
80
70
Putaran (rad/det) atau Torsi Beban (N.m)
Simulasi diatur pada kondisi start, steady state dan
perubahan referensi putaran dan bila terjad perubahan
beban.
Dari optimasi GA diperoleh nilai h=300 dan 𝛽 = 35,
7
Wm.Aktual (rad/det)
Wm.ref.(rad/det)
Torsi(N.m)
60
50
40
30
20
10
0
-10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
time[detik]
Gambar 14. Respon Putaran Motor untuk setiap kondisi
Arus Sekunder Motor
40
0,12
0,12
0,12
Ia
30
Ib
Ic
t1
20
t2
t3
38,09 rad/det.
38,09 rad/det.
76,18 rad/det.
5,10 A
5,10 A
8,2 A
0
-10
-20
-30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
time[detik]
Gambar 15. Arus Stator untuk setiap kondisi
Tegangan Motor
500
Va (Volt)
t1
t2
t3
Ampere
10
Gambar 15 merupakan arus stator pada setiap kondisi
perubahan yang terjadi, daerah t1 menunjukkan saat
putaran 38,09 rad/detik pada saat beban nol (motor
tanpa beban), daerah t2 menunjukkan saat putaran
motor 76,18 rad/detik pada beban nol, dan daerah t3
menunjukkan saat putaran 76,18 rad/detik untuk beban
penuh 31,63 N.m.
Tabel 4. Respon arus stator
Parameter terukur
Daerah
Putaran
Arus
0
-500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
time[detik]
0.6
0.7
0.8
0.9
1
Gambar 16. Merupakan output tengangan inverter
yang menjadi input tegangan bagi motor induksi 3
phasa,
Tabel 3. Respon Tegangan Motor
Parameter terukur
Putaran
Periode (T)
Vm
38,09 rad/det. (t=0 s/d 0,3 dtk)
76,18 rad/det. (t=0,3 s/d 1 dtk
0,091 detik
0,044 detik
466,6
466,6
0
-500
500
Vc (Volt)
Untuk kondisi transient dan perubahan referensi
kecepatan overshoot arus yang terjadi sebesar 40, 29
Ampere dan 10,5 ampere
Vb (Volt)
500
0
-500
Gambar 16. Tegangan Motor pada saat perubahan
referensi kecepatan dan Torsi beban
Respon Error Torsi, Torsi Reference dan Torsi Estimasi
400
300
Terlihat bahwa pada saat perubahan referensi kecepatan
menjadi lebih cepat frekuensi tegangan motor juga
1
semakin besar (𝑓 = )
DT
Te
Tr
200
100
𝑇
0
Gambar 17. Merupakan respon dari torka
elektromagnetik dimana pada saat start dan perubahan
setting kecepatan terjadi ripple torka sebesar 310 N,m
dan 280 N.m
-100
-200
-300
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
4
x 10
Gambar 17. Torka Elektromagnetik
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
8
Daftar Pustaka
[1] Soebagio, Model mesin AC pada koordinat d-qn,
Gambar 18. Fluks stator terhadap koordinat
sumbu d dan q
7. Penutup
Dari hasil simulasi yang telah dilakukan dapat ditarik
kesimpulan yaitu :
1. Pada saat start motor dengan beban nol dan putaran
0,5 putaran nominal (38,09 rad/det) terjadi
overshoot 9,43 rad.det(19,84%), rise time 0,007875
detik dan settling time 0,12 detik.
2. Pada saat motor terjadi perubahan putaran referensi
naik 100% menjadi 76,18 rad/det. dengan beban nol
terjadi overshoot 15,74 rad.det(17,12%), rise time
0,0094 detik dan settling time 0,12 detik.
3. Pada saat motor diberi beban penuh 31,63 N.m dan
putaran (76,18 rad/det) terjadi overshoot 4,45
rad.det(5,51%), rise time 0, detik peak time 0,0086
detik dan settling time 0,12 detik.
4. Dari gambar 10 kita lihat bahwa sistem kokoh
(robust) untuk perubahan beban yang terjadi.
Ucapan Terima kasih
Ucapan terima
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
Materi Kuliah Mesin Listrik Lanjut, ITS, 2006
[2] D. Casadei, G. Serra, A. Tani, and L.Zarri,
“Assessment of direct torque control for induction
motor drives”, Buletin of the Polish academy of science
tech. sciences, vol. 54, No.3, 2006.
[3] Bimal Kr. Bose, Modern Power Electronics and AC
drives, Prentice Hall PTR, 2002.
[4] D. Casadei, Giovanni Serra, “FOC and DTC: two
variable scheme for induction motors torque control”,
Trans. On Power Electronics, Vol. 17, No. 5,
September 2002.
[5] I. Takahashi, T. Noguchi,” A new quick-response
and high-efficiency control strategy of an induction
motor”, IEEE, Trans. Ind. Appl., IA-22(5): 820-827,
1996.
[6] M. Abid, Y. Ramdani, A. Aissaoui, A.
Zeblah,”Sliding mode speed and flux control of an
induction machine”, Journal of Cybernetics and
Informatics, ISSN: 1336-4774, vol. 6, 2006.
[7] Paul C. Krause,” Analysis of Electric Machinery”,
McGraw-Hill, 1987.
[8] Ned mohan,” Advance electric drives analysis,
control and modeling using simulink”, MNPERE,
Minneapolis, 2001.
[9] O. Barambones, A. J. Garrido, F.J. Maseda. “A
robust field oriented control of induction motor with
flux observer and speed adaptation”. Proc. IEEE-ATFA,
2003.
[10] Petar R. Matic, Branko D. Blanus, Slobodan N
Vukosavic,“A novel direct torque control and flux
control algorithm for the induction motor”,IEEE, 2003.
[11] T. Brahmananda Reddy, D. Subbarayudu, J.
Amarnath,” Robust sliding mode speed controller for
hybrid SVPWM base direct torque control of induction
motor”, World Jurnal of Modelling and Simulation,
ISSN 1 746-7233, England, vol 3, 2007.
[12] Wilfrid Perruquetti, Jean Pierre Barbot,” Sliding
mode control in Engineering”, Marcel and Dekker, Inc.
New York-Basel, 2002.
[13] Arman Jaya, Mauridhi Heri Purnomo, Soebagio,
“Pengaturan Kecepatan Motor Induksi Tanpa Sensor
Kecepatan Menggunakan Metode Fuzzy Sliding Mode
Control Berbasis Direct Torque Control”, Jurusan
Teknik Elektro, Fakultas Teknologi Industri, ITS. 2009.
[14] Ching-Chang Wong, Shih-Yu Chang, “Parameter
Selection in the Sliding Mode Control Design Using
Genetic Algorithms, Tamkang Journal of Science and
Engineering, Vol. 1, No. 2, pp. 115-122, 1998
[15] T. Cao-Minh Ta, C. Chakraborty, Y. Hori,
Efficiency Maximization of Induction Motor Drives for
Electric Vehicles Based on Actual Measurement of
Input Power, Department of Electrical Engineering,
University of Tokyo, Japan
Seminar Teknik Komputer, Kendali dan Elektronika Mei 2011
Oktavianus Kati, dilahirkan
di Makassar 26 Oktober
1976,
Menamatkan
Pendidikan Dasar pada SD
Negeri Inpres Bertingkat
Rappo Jawa Makassar
tahun
1988,
Pendidikan
Menengah pada SMP Negeri
4 Makassar tahun 1991,
SMA Negeri 4 Surabaya
tahun 1994, dan Sarjana pada Universitas Hasanuddin
(Konsentrasi Teknik Energi) pada tahun 1999. Dari
tahun 2000-2002 aktif sebagai tenaga ahli pada PT.
Wesitan Konsultan Pembangunan Wamena, tahun
2003 terangkat sebagai tenaga Edukatif (PNS) pada
Universitas Cenderawasih (UNCEN) JayapuraPapua. Dari tahun 2005-2007 aktif sebagai kepala Lab
pada Laboratorium Mesin-mesin Listrik UNCEN. Dan
dari tahun 2007-2009 menjabat ketua Program Studi D3
Teknik Elektro UNCEN, tahun 2009 hingga sekarang
tercatat sebagai mahasiswa Pascasarjana pada
Program Studi Teknik Elektro konsentrasi Teknik
Komputer, Kendali dan Elektronika Universitas
Hasanuddin Makassar.
Email : [email protected]
 Mahasiswa Program Pascasarjana Teknik Elektro UNHAS No.Stambuk P2700209049
9