BAB 16. MEDAN LISTRIK 16.1 Muatan Listrik

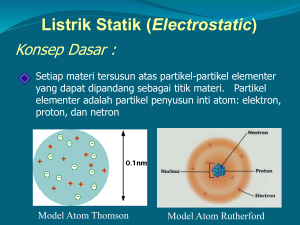
DAFTAR ISI
DAFTAR ISI..............................................................................1
BAB 16. MEDAN LISTRIK........................................................2
16.1 Muatan Listrik..............................................................2
16.2 Muatan Listrik dalam Atom .........................................2
16.3 Isolator dan Konduktor ................................................3
16.4 Hukum Coulomb .........................................................3
16.5 Medan Listrik dan Kondusi Listrik ...............................5
16.6 Quis 16......................................................................13
1
BAB 16. MEDAN LISTRIK
16.1
Muatan Listrik
Sejarah pengamatan listrik diawali oleh pengamatan Thales (600 SM) yang mengamati bahwa
batu ambar yang digosok wol akan menarik potongan jerami. Kemudian W. Gilbert (1600)
menyatakan bahwa sifat batu ambar tersebut sebagai listrik (electric). Adanya dua macam pelistrikan
yang diterangkan dengan adanya dua macam muatan listrik, ditunjukkan oleh Du Fay (1700), yaitu
“Muatan sejenis tolak menolak dan muatan tak sejenis tarik menarik”. Tanda positif dan negative
diusulkan oleh B. Franklin (1706-1790).
Selain pengamatan kelistrikan juga berkembang pengamatan tentang kemagnetan. Kedua
bidang ilmu ini berkembang secara agak terpisah sampai 1820, hingga H.C. Oersted (1777-1851)
mengamati adanya hubungan listrik dan magnet, yaitu bahwa arus listrik dalam sebuah kawat dapat
mempengaruhi sebuah jarum kompas magnetic. Kemudian Michael Faraday (1791-1867)
mengembangkan elektromagnetisme dan J.C Maxwell (1831-1879) merumuskan hukum-hukum
elektromagnetisme yang dikenal dengan persamaan Maxwell.
Di zaman B. Franklin muatan listrik dianggap fluida kontinyu. Baru setelah R.A. Millikan
melakukan eksperimen tetes cairan, diperoleh bahwa muatan listrik terkuantisasi, yaitu muatan
mempunyai harga kelipatan bulat dari muatan elementer e. Satuan muatan adalah Coulomb (C) dan
satu Coulomb adalah banyaknya muatan yang mengalir persatuan luas dalam satu detik jika arus
yang mengalir sebesar 1 Ampere.
16.2
Muatan Listrik dalam Atom
Atom secara kelistrikan bermuatan netral, terdiri atas inti dan electron yang mengelilinginya. Inti
atom bermuatan positif karena di dalamnya terdapat proton yang bermuatan positif dan netron yang
tidak mempunyai muatan. Electron dalam atom biasanya digunakan sebagai muatan dasar atau
satuan dasar untuk muatan. Muatan proton dan electron sama besar tetapi berlawanan tanda. Muatan
proton adalah e dan muatan electron adalah –e . Semua muatan merupakan kelipatan bilangan bulat
dari satuan dasar muatan. Proton memiliki massa sekitar 2000 kali massa electron.
2
Hukum kekekalan muatan merupakan suatu hukum dasar dari alam. Perpindahan electron
dapat terjadi ketika suatu benda digosokkan antara satu dengan lainnya. Ketika sebuah benda A
digosokkan dengan benda B maka akan ada electron yang berpindah sehingga benda A tersebut
akan kekurangan electron (mengakibatkan menjadi bermuatan positif), dan sebaliknya benda B akan
kelebihan electron (menjadikan bermuatan negative).
16.3
Isolator dan Konduktor
Pergerakan sebuah elektron dalam beberapa bahan/material akan menentukan nantinya bahan
tersebut sebagai bahan yang dapat mengalirkan arus listrik atau tidak. Sebuah bahan konduktor
adalah bahan yang mampu mengalirkan arus listrik (elektron dapat bergerak bebas) misalnya besi.
Sedangkan material yang senua elektronnya tidak bebas bergerak atau dengan kata lain semua
elektronnya terikat kuat pada atom-atomnnya disebut dengan isolator.
16.4
Hukum Coulomb
C.A. Coulomb (1736-1806) mendapatkan bahwa gaya interaksi antara dua muatan titik
sebanding dengan muatan masing-masing dan berbanding terbalik dengan kuadrat jarak antara
kedua muatan tersebut.
F∞
q1 q 2
r2
dengan F = gaya Coulomb
atau
F=
q1 q 2
4πε 0 r 2
1
q = muatan litrik
ε0 = permitivitas vakum = 8,85 x 10-12 C2/Nm2
(11.1)
r = jarak antar muatan
1
4πε 0
= 9 x 109 Nm2/C
Beberapa hal yang penting sehubungan dengan Persamaan (1) yang dikenal sebagai hukum
Coulomb itu adalah : persamaan hanya berlaku untuk muatan titik (partikel), Tetapan pembanding
diambil berbentuk 1/4πε0 agar rumus yang diturunkan dari persamaan di atas tidak mengandung
faktor 4π, bentuk hukum Coulomb dengan tetapan pembanding 1/4πε0 ini berlaku jika menggunakan
sistem satuan MKS dan persamaan hanya berlaku di vakum.
3
Jika lebih dari dua muatan yang berinteraksi maka berlaku prinsip superposisi, yaitu gaya pada
q1, F1, oleh beberapa muatan adalah superposisi gaya interaksi antara q1 dengan masing-masing
muatan.
v
v
v
v
F1 = F12 + F13 + F14 + ...
(11.2)
v
di mana F12 adalah gaya yang bekerja pada q1 oleh q2.
Persamaan (11.2) hanya berlaku jika interaksi tidak saling mengganggu, yaitu posisi muatan
dianggap tetap.
Contoh 1
Uang logam tembaga mempunyai massa 3,1 g. Karena uang tersebut netral secara listrik, maka
muatan positif dan negatif sama banyaknya. Jika diketahui muatan inti positif atom tembaga 4,6 x 1018 C, tentukan :
a. Besarnya muatan dalam uang logam tersebut.
b. Jarak pisah yang diperlukan agar timbul gaya sebesar 4,5 N.
Jawab
a. Banyaknya atom tembaga, N, dalam uang logam
N
m
=
N0 M
di mana N0 = bilangan Avogadro = 6 x 1023 atom/mol
m = massa uang
M = berat atom tembaga = 64 g/mol
(6 x 10 23 atom/mol)(3,1g)
N=
= 2,9 x 10 22 atom
64 g/mol
Maka
Jadi muatan q adalah
q = (4,6 x 10-18 C/atom)(2,9 x 1022 atom) = 1,3 x 105 C.
Dari jawaban a didapat q1 = q2 = q = 1,3 x 105 C
q1 q 2
1 q2
F=
=
4πε 0 r 2
4πε 0 r 2
1
1 4πε 0
9 x 10 9
5
= 1,3 x 10
= 5,8 x 10 9 m
r=q
F
4,5
Hasil ini adalah sekitar 910 kali jari-jari bumi yang menganjurkan kepada kita bahwa tidaklah mungkin
untuk mengganggu kenetralan benda.
Contoh 2
Gambar di bawah memperlihatkan tiga muatan tetap q1, q2 dan q3. Berapakah gaya yang bekerja
pada q1 ? Anggaplah q1 = -1 x 10-6 C, q2 = +3 x 10-6 C, q3 = -2 x 10-6 C, r12 = 15 cm, r13 = 10 cm dan
θ = 30°.
4
y
q3
r13
θ
F12
q1
r12
θ
q2
x
F13
Jawab
v
Untuk menghitung besarnya gaya, maka tanda-tanda muatan diabaikan dan arah gaya-gaya F12 dan
v
F13 diberikan di gambar.
q1 q 2
1 q1 q3
=
...
=
1
,
2
N
F
=
= ... = 1,8 N
13
4πε 0 r 2
4πε 0 r 2
v
Komponen gaya resultan F1 yang bekerja pada q1 adalah
F12 =
1
F1x = F12x + F13x = F12x + F13 sin θ = … = 2,1 N
Besarnya F1 adalah
F1y = F12y + F13y = 0 - F13 cos θ = … = -1,6 N
F1 = F1x + F1 y = ... = 2,64 N
2
2
Sudut yang dibentuk F1 dengan sumbu x adalah φ = arctg (F1y/ F1x) = -37,3°
16.5
Medan Listrik dan Kondusi Listrik
Medan listrik adalah ruang di sekitar muatan listrik. Jika sebuah muatan uji ditempatkan dalam
ruang di dekat tongkat bermuatan, maka sebuah gaya elektrostatis akan bekerja pada muatan uji. Hal
ini dikatakan ada medan listrik dalam ruang tersebut.
Di zaman Faraday, gaya yang bekerja tersebut dianggap sebuah interaksi sesaat yang
langsung atau dikenal dengan istilah aksi pada suatu jarak. Secara skematis diberikan
muatan ⇔ muatan
Pandangan aksi pada suatu jarak di mana informasi dari q1 diteruskan pada saat itu juga,
ternyata tidak sesuai dengan eksperimen. Pandangan yang sesuai dengan eksperimen dan
digunakan sekarang adalah
5
muatan ⇔ medan ⇔ muatan
Artinya muatan q1 menimbulkan medan listrik di ruang sekitarnya dan medan tersebut bekerja
pada q2.
v
Dalam membahas medan listrik digunakan pengertian kuat medan. Kuat medan listrik, E ,
adalah vektor gaya Coulomb yang bekerja pada satu satuan muatan yang terletak pada titik dalam
medan gaya.
v
v F
E=
q0
v
E=
atau
1
q
v2
4πε 0 r
(11.3)
q0 = muatan uji (q0 << q dan q0 → 0)
di mana q = muatan sumber
Satuan kuat medan listrik adalah N/C.
Hal-hal yang penting tentang persamaan (11.3) adalah berlaku jika muatan sumber berupa titik
(partikel), pusat sistem pada muatan sumber, besaran yang digunakan sistem satuan MKS,
persamaan hanya berlaku di vakum. Untuk distribusi muatan titik berlaku
v
v
E = ∑ En
(11.4)
Sedangkan untuk muatan kontinyu
v
v
E = ∫ dE
(11.5)
Contoh 3
Dua muatan masing-masing q1 = 1 x 10-6 C, q2 = 2 x 10-6 C, terpisah sejauh 10 cm. Di titik manakah
pada garis yang menghubungkan kedua muatan tersebut medan listriknya sama dengan nol ?
Jawab
Seperti tampak pada gambar 2, titik tersebut harus terletak di antara kedua muatan karena hanya di
situlah gaya yang dikerahkan kedua muatan tersebut pada muatan uji saling bertentangan, tak peduli
muatan uji positif atau negatif.
q1
x
q2
P
l
Gambar 2
6
Maka
q1
q1
1
=
2
4πε 0 x
4πε 0 (l − x) 2
1
E1 = E2
Dengan memecahkannya untuk x diperoleh
x=
1
1 + q 2 q1
= ... = 4,1 cm
Jadi titik di mana medan listriknya sama dengan nol adalah pada jarak 4,1 cm sebelah kanan q1.
Lengkapilah langkah-langkah yang tidak diberikan di atas dan mengapa akar kedua dari persamaan
kuadratis yang dihasilkan tidak diikutsertakan.
Konsep garis gaya diusulkan oleh Michael faraday untuk memvisualkan medan listrik (dan
medan magnet). Garis gaya adalah garis khayal yang ditarik sedemikian hingga arahnya di
sembarang titik (arah tangennya) sama dengan arah medan di titik yang bersangkutan.
Gambar 11.1 Konsep garis gaya
Hubungan garis gaya dengan medan listrik, garis singgung kepada sebuah garis gaya pada
setiap titik memberikan arah E di titik tersebut, dan Garis gaya digambarkan sebagai banyaknya garis
persatuan luas (yang tegak lurus pada garis-garis tersebut) sebanding dengan besar E, yaitu untuk
medan kuat berarti garis gaya rapat, dan garis gaya renggang berarti medan lemah.
Pada Gambar 4 diberikan garis gaya untuk (a) muatan tunggal positif, (b) dipol listrik dan (c)
dua muatan positif. Perhatikan bahwa arah garis gaya keluar dari muatan positif dan masuk ke
muatan negatif.
Gambar 11.2 Arah garis gaya
7
Fluks medan listrik, ΦE, adalah banyaknya garis gaya yang menembus suatu satuan luas yang
v
tegak lurus pada kuat medan listrik, E . ΦE positif jika garis gaya di mana-mana menuju keluar dan
sebaliknya. Fluks medan listrik adalah penting karena Hukum Gauss yang merupakan salah satu dari
empat persamaan dasar elektromagnetisme dinyatakan dengan fluks medan listrik.
Gambar 11.3 Fluks medan magnet
Perhatikan kurva S1, S2, S3 dan S4 pada Gambar 11.3 yang menyatakan perpotonganperpotongan di antara empat permukaan tertutup hipotetik dengan bidang gambar. Dari Gambar 11.3,
maka ΦE positif untuk permukaan S1, ΦE negatif untuk permukaan S2, dan ΦE nol untuk permukaan
S3.
Untuk mendefinisikan ΦE dengan tepat, tinjau Gambar 11.4 berikut yang menyatakan
permukaan tertutup sebarang di dalam medan listrik tak uniform.
8
Gambar 11.4 Fluks magnetik dalam medan listrik
v
Perhatikan bagian yang diperbesar yang ditandai dengan x, y dan z. Pada x, θ > 90° ( E
v
v
menuju ke dalam); pada y, θ = 90° ( E sejajar permukaan) dan pada z, θ < 90° ( E menuju ke luar).
v
Elemen luas, ΔS , diambil sebagai normal pada permukaan dan digambarkan ke arah luar.
Sebuah definisi setengah kuantitatif mengenai fluks adalah
v v
Φ E ≅ ∑ E.ΔS
(11.6)
Definisi fluks listrik yang tepat didapat di dalam limit diferensial dari persamaan (11.6), yaitu
dengan mengganti penjumlahan dengan integral
v v
Φ E = ∫ E . dS
(11.7)
Fluks medan listrik adalah besaran skalar dan satuannya adalah Nm2/C.
Contoh 4
Gambar 7 memperlihatkan
sebuah silinder tertutup hipotetik yang jari-jarinya R dan berada dalam
v
medan listrik E yang uniform. Sumbu silinder sejajar dengan medan tersebut. Berapakah ΦE untuk
permukaan ini ?
9
Jawab
Fluks ΦE dituliskan sebagai penjumlahan dari (a) integral terhadap permukaan penutup silinder kiri,
(b) permukaan silinder dan (c) permukaan penutup sebelah kanan, yaitu
v v
Φ E = ∫ E. dS
v v
v v
v v
= ∫ E. dS + ∫ E. dS + ∫ E. dS
a
b
c
= ∫ E cos180 dS + ∫ E cos 90 dS + ∫ E cos 0 dS
= − ES + 0 + ES
=0
v
Dengan hukum Coulomb kita dapat menghitung E di berbagai titik jika distribusi muatan
diketahui. Metode ini meskipun selalu dapat dipakai merupakan metode langsung yang banyak
memerlukan tenaga.
Karena itu di sini diperkenalkan hukum Gauss yang merupakan bentuk lain dari hukum
Coulomb. Dengan perumusan ini maka perhitungan tidak memerlukan banyak tenaga. Keterbatasan
dari hukum Gauss adalah tidak semua persoalan dapat dipecahkan. Perumusan Gauss lebih berguna
untuk lebih mendalami soal karena perumusan tersebut memberikan lebih dari sekedar pemecahan
soal praktis.
Hukum Gauss berbunyi : “Jumlah garis gaya yang keluar dari suatu permukaan tertutup
sebanding dengan jumlah muatan netto yang dilingkupi oleh permukaan tertutup tersebut”.
Permukaan tertutup di sini disebut permukaan Gauss.
ε 0Φ E = q
atau
v
v
ε 0 ∫ E . dS = q
(11.8)
dengan q adalah muatan netto yang dicakup permukaan Gauss. Muatan di luar permukaan
tidak memberikan kontribusi pada q.
Kembali ke Gambar 11.4, ΦE = 0 untuk permukaan S4 karena jumlah aljabar muatan di dalam
permukaan tersebut adalah nol.
10
v
Hukum Gauss dapat digunakan untuk menghitung E dari benda bermuatan yang mempunyai
bentuk khusus, yaitu jika simetri dari distribusi muatan adalah tinggi, misalnya bola, pelat tipis, silinder.
Contoh 5
Distribusi muatan simetri bola. Gambar di bawah memperlihatkan sebuah distribusi muatan berbentuk
bola dengan jari-jari R. Muatan tersebar sama rata di dalam bola.
v
Tentukan E untuk titik-titik (a) di dalam dan (b) di luar distribusi muatan tersebut.
Jawab
Di dalam bola, muatan yang dilingkupi oleh permukaan S1 sama dengan muatan total, q1 = q, maka
v v
1 q
ε 0 ∫ E. dS = ε 0 E (4πr 2 ) = q1 = q atau
E=
4πε 0 r 2
Di luar bola, muatan yang dilingkupi oleh permukaan S2 adalah
q2 = q
4
3
4
3
πr 3
πR 3
3
atau
⎛r⎞
q 2 = q⎜ ⎟ , maka
⎝R⎠
3
v v
⎛r⎞
2
ε 0 ∫ E. dS = ε 0 E (4πr ) = q 2 = q⎜ ⎟ atau
⎝R⎠
E=
qr
4πε 0 R 3
1
Contoh 6
Garis muatan tak hingga. Gambar 9 memperlihatkan sebagian dari garis muatan takvhingga. Rapat
muatan linier, λ, adalah konstan untuk semua titik pada garis tersebut. Tentukan E di titik yang
berjarak r dari garis tersebut.
11
Jawab
Muatan yang dicakup oleh permukaan Gauss adalah λh, maka
v v
ε 0 ∫ E . dS = q
ε 0 E (2πrh) = λh
E=
λ
2πε 0 r
Contoh 7
Lembar muatan tak hingga. Gambar 10 memperlihatkan sebagian dari lembar muatan tak vhingga
yang tipis dan bersifat tak hantar. Rapat muatan permukaan, σ, adalah konstan. Tentukan E pada
suatu jarak r di muka lembar tersebut.
Jawab
v
Karena E tidak menembus permukaan silinder maka tidak ada kontribusi fluks dari sumber ini, maka
v v
ε 0 ∫ E . dS = q
ε 0 ( EA + EA) = σA
atau
E=
σ
2ε 0
Contoh 8
Sebuah penghantar bermuatan. Gambar 11 memperlihatkan sebuah penghantar yang mengangkut
sebuah muatanv pada permukaannya. Rapat muatan permukaan, σ, umumnya berubah dari titik ke
titik. Tentukan E yang dekat jaraknya di atas permukaan tersebut.
Jawab
v
Karena E sama dengan nol di dalam penghantar, maka satu-satunya kontribusi kepada fluks adalah
penutup bidang seluas A di luar penghantar. Jadi
12
v
v
ε 0 ∫ E . dS = q
ε 0 EA = σA
E=
16.6
σ
ε0
Quis 16
1.
Dua buah bola identik yang mempunyai muatan masing-masing q1 dan q2, dipisahkan
dalam jarak 3 cm, ternyata mengalami gaya tolak sebesar 3,6 x 10-4 N. Kemudian kedua
bola tersebut saling disentuhkan dan dipisahkan lagi pada jarak 3 cm, ternyata gaya
tolaknya menjadi 2,0 x 10-4 N. Berapakah muatan q1 dan q2.
2.
Tiga buah muatan disusun berderet seperti gambar di bawah ini
Jika q1 = + 1 μC, q2 = - 2 μC, q3 = + 3 μC dan a = 5 cm, tentukan : (a) Besar dan arah
gaya Coulomb yang bekerja pada q2 (b) Besar dan arah kuat medan listrik di titik P
3.
Sebuah bola bermassa 1,0 x 10-3 g mengangkut muatan sebesar 2,0 x 10-8 C. Bola
tersebut digantungkan dengan benang sutera pada lembar tak hantar yang besar yang
bermuatan dan membuat sudut 30o seperti tampak pada Gambar berikut. Hitunglah rapat
muatan permukaan, σ, untuk lembar tersebut ! (Catatan : Kuat medan listrik untuk
lembar tak hingga adalah E = σ / 2ε 0 )
13