Konsep Dasar Listrik dan Elektro 2

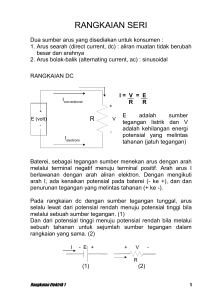
Tek nik I ns ta l as i L is tr ik
Kegiatan Belajar 2
HUKUM RANGKAIAN ARUS
Tujuan Khusus Pembelajaran
Peserta dapat :

Menjelaskan hukum Ohm dan hukum Kirchhoff

Menggunakan hukum Ohm dan hukum Kirchhoff dalam pengerjaan soal

Mengetahui macam-macam rangkaian dasar dalam teknik listrik

Memberikan contoh praktis rangkaian dasar teknik listrik
1.
Hukum Ohm
Kita hubungkan sebuah tahanan pada suatu tegangan dan membentuk suatu
rangkaian arus tertutup, maka melalui tahanan tersebut mengalir arus yang
besarnya tertentu. Besar kecilnya arus tergantung pada tahanan dan tegangan
yang terpasang.
Penjelasan tentang hubungan antara tegangan, kuat arus dan tahanan pada
suatu rangkaian arus diperlihatkan oleh percobaan berikut :
Percobaan :
a) Pengukuran kuat arus pada bermacam-macam tegangan (2V,
4V, 6V) dan besarnya tahanan konstan (10).
I = 0,2 A
A
U=2V
Gambar 2.1
I = 0,4 A
I = 0,6 A
A
A
R = 10
U=4V
R = 10 
U=6V
R = 10 
Arus pada bermacam-macam tegangan
Perhatikan : Kuat arus I berbanding langsung dengan tegangan U
Penerapan Konsep Dasar Listrik dan Elektronika
50
Tek nik I ns ta l as i L is tr ik
Percobaan :
b) Pengukuran kuat arus pada bermacam-macam tahanan (10,
20, 30).dan besarnya tegangan konstan (6V).
I = 0,6 A
A
I = 0,3 A
A
R = 10 
U=6V
Gambar 2.2
U=6V
I = 0,2 A
A
R = 20 
U=6V
R = 30 
Arus pada bermacam-macam tegangan
Perhatikan : Kuat arus I berbanding terbalik dengan tahanan R
Secara umum berlaku :
Kuat arus I adalah : a) berbanding langsung dengan tegangan U
b) berbanding terbalik dengan tahanan R
Hal tersebut diringkas kedalam suatu formula, maka kita peroleh hukum Ohm.
Kuat arus I =
Tegangan U
Tahanan R
Dalam simbol formula :
I=
U
R
I
Kuat arus dalam A
U Tegangan dalam V
R Tahanan dalam 
Melalui penjabaran persamaan kita dapatkan dua bentuk hukum Ohm yang lain
U=R.I
R=
U
I
Dalam hal ini digunakan satuan Volt, Ampere dan Ohm.
Penerapan Konsep Dasar Listrik dan Elektronika
51
Tek nik I ns ta l as i L is tr ik
1.1.
Grafik tegangan fungsi arus
Kita tempatkan tegangan termasuk juga arusnya kedalam suatu sistim koordinat
yang bersudut siku-siku (pada sumbu horisontal tegangan U sebagai besaran
yang diubah-ubah dan pada sumbu vertikal arus I yang sesuai sebagai besaran
yang berubah) dan titik ini satu sama lain saling dihubungkan, maka kita
dapatkan grafik tegangan fungsi arus.
Untuk percobaan a) yang dilaksanakan dengan tahanan R = 10  diperoleh
grafik sebagai berikut :
A
0,7
0,6
0,5
0,4
0,3
0,2
0,1
1
2
3
4
5
6
7V
Gambar 2.3
U
Grafik tegangan fungsi arus
Pada tahanan yang tetap konstan maka grafiknya lurus seperti diperlihatkan
pada gambar.
Contoh :
1. Suatu kompor listrik untuk 220 V menyerap arus sebesar 5,5 A.
Berapa besarnya tahanan kompor listrik ?
Diketahui :
U = 220 V;
Ditanyakan :
R
Jawaban :
R=
U
;
I
I = 5,5 A
R=
220 V
 40 Ω
5,5 A
2. Pada suatu tahanan tertulis data 4 k dan 20 mA.
Berapa besarnya tegangan maksimum yang boleh terpasang ?
Penerapan Konsep Dasar Listrik dan Elektronika
52
Tek nik I ns ta l as i L is tr ik
R = 4 k = 4000 
Diketahui :
I = 20 mA = 0,02 A
Ditanyakan :
U
Jawaban :
U=I.R
U = 4000  . 0,02 A = 80 V
3. Pada gambar 2.4 ditunjukkan grafik tegangan fungsi arus untuk tiga
buah tahanan. Berapa besarnya nilai-nilai tahanan tersebut ?
mA
20
Grafik a
Grafik b
15
10
Grafik c
5
Gambar 2.4
20
10
Grafik tegangan fungsi arus
30
40 V
U
Jawaban :
Grafik a : Untuk U = 10 V besarnya arus I = 20 mA = 0,02 A
R=
U
;
I
R=
10 V
 500 Ω
0,02 A
Grafik b : Untuk U = 40 V besarnya arus I = 20 mA = 0,02 A
R=
40 V
 2000 Ω = 2 kΩ
0,02 A
Grafik c : Untuk U = 30 V besarnya arus I = 5 mA = 0,005 A
R=
30 V
 6000 Ω = 6 kΩ
0,005 A
Penerapan Konsep Dasar Listrik dan Elektronika
53
Tek nik I ns ta l as i L is tr ik
2.
Rangkaian seri tahanan
Suatu rangkaian seri tahanan terbentuk, jika untuk tegangan yang terpasang
pada semua tahanan berturut-turut mengalir arus yang sama.
I
R1
R2
R3
U
Gambar 2.5
Rangkaian seri tahanan
Penjelasan tentang tegangan, arus dan tahanan untuk rangkaian seri dapat
diperhatikan pada percobaan berikut ini :
Percobaan :
a) Pengukuran arus I dengan memasang alat pengukur arus
didepan, diantara dan dibelakang tahanan.
I =0,1A
I =0,1A
I =0,1A
A
A
R1=20
A
R2=40
R3=60
U=12V
Gambar 2.6
A
Arus pada rangkaian seri
I=0,1A
Pada rangkaian seri kuat arus di semua tahanan besarnya sama.
Disini pada rangkaian arus tak satupun tempat bagi elektron-elektron untuk
dapat keluar. Yaitu arus yang tidak pernah digunakan !
Percobaan :
b) Pengukuran tegangan U1, U2, U3, Utotal dengan alat pengukur
tegangan dan pengukuran arus I dengan alat pengukur arus
pada rangkaian seri yang diberikan.
Penerapan Konsep Dasar Listrik dan Elektronika
54
Tek nik I ns ta l as i L is tr ik
Hasil pengukuran : U1 = 2 V;
U2 = 4 V;
I=0,1A
Utotal = 12 V; I = 0,1 A
U3 = 6 V
U1 =2V
U2 =4V
U3 =6V
R1=20
R2=40
R3=60
V
V
V
A
Utotal =12V
V
Gambar 2.7 Tegangan
pada rangkaian seri
Kita jumlahkan tiga tegangan bagian (tegangan jatuh) U1, U2, U3, maka kita
dapatkan, bahwasanya jumlah tegangan-tegangan tersebut sama dengan
tegangan terpasang Utotal.
Secara umum dinyatakan :
Tegangan total sama dengan jumlah tegangan bagian
Utotal = U1 + U2 + U3 +   
Tahanan total rangkaian seri secara langsung dapat ditentukan dengan suatu
alat pengukur tahanan. Namun dalam praktik lebih banyak dipilih metode tidak
langsung, yaitu melalui pengukuran tegangan dan arus, tahanan dihitung
dengan bantuan hukum Ohm.
R total =
Utotal
I
Rtotal =
12 V
= 120 Ω
0,1 A
Dengan demikian terbukti :
Tahanan total sama dengan jumlah tahanan bagian.
Rtotal = R1 + R2 + R3 +   
Penerapan Konsep Dasar Listrik dan Elektronika
55
Tek nik I ns ta l as i L is tr ik
Dengan demikian dapat diterangkan, bahwa arus berturut-turut harus
mengatasi/menguasai semua tahanan bagian.
Karena tahanan total diganti juga dengan tahanan secara tersendiri, yang mana
hal ini disebut juga sebagai tahanan pengganti (Rpengganti).
Kita bandingkan perbandingkan tegangan
U1 2V 1


U2 4V 2
U2 4V 2


U3 6V 3
Utotal 12V 6


U1
2V
1
U1 : U2 : U3 = 2V : 4V : 6V = 1 : 2 : 3
perbandingan untuk tahanan yang ada
R1 20 Ω 1


R 2 40 Ω 2
R 2 40 Ω 2


R3 60 Ω 3
Rtotal 120 Ω 6


R1
20 Ω
1
R1 : R2 : R3 = 20 : 40 : 60 = 1 : 2 : 3,
Dengan demikian kita dapatkan, bahwasanya kedua hal tersebut sesuai/cocok
satu sama lain.
Ini membuktikan :
Tegangan bagian satu sama lain mempunyai karakteristik seperti
tahanan yang ada.
misal
U1 R1
=
U2 R 2
U2 R 2
=
U3 R 3
Utotal R total
=
U1
R1
U1 : U2 : U3 = R1 : R2 : R3
Hal tersebut dapat diterangkan sebagai berikut :
Penerapan Konsep Dasar Listrik dan Elektronika
56
Tek nik I ns ta l as i L is tr ik
Disetiap tahanan mengalir arus yang sama. Pada tahanan yang sama arus
tersebut menimbulkan tegangan jatuh yang sama pula. Pada tahanan yang
berbeda arus yang mengalir mengakibatkan terjadinya tegangan jatuh yang
berbeda pula, untuk tahanan yang besar tahanan jatuhnya besar, untuk tahanan
kecil tegangan jatuhnya kecil.
Pada pemakaian, seperti misalnya lampu pijar, jarang dihubungkan secara seri,
disini kerugian suatu pemakai/beban yang seluruhnya terhubung seri dengan
yang lain maka dapat terjadi beban tersebut tanpa arus. Salah satu pemakaian
yang ada yaitu lampu hias warna-warni atau rangkaian seri pembangkit
tegangan
Contoh :
1. Tiga tahanan R1 = 50, R2 = 100 dan R3 = 200 terhubung
seri pada 175V.
Berapa besarnya tahanan total, arus dan tegangan jatuh ?
Buatlah gambar rangkaiannya !
Diketahui :
R1 = 50; R2 = 100; R3 = 200; U = 175V
Ditanyakan : Rtotal, I, U1, U2, dan U3
Jawaban :
Rtotal = R1 + R2 + R3
Rtotal = 50 + 100 + 200 = 350
I=
U
;
R total
I=
175V
 0,5A
350Ω
U1 = I . R1 ;
U1 = 0,5A . 50 = 25V
U2 = I . R2 ;
U2 = 0,5A . 100 = 50V
U3 = I . R3 ;
U3 = 0,5A . 200 = 100V
I
U1
U2
U3
R2=50 R2=100 R3=200
U=175V
Gambar 2.8
Skema rangkain soal no. 1
Penerapan Konsep Dasar Listrik dan Elektronika
57
Tek nik I ns ta l as i L is tr ik
2. Lampu pijar 10V/0,2A dan lampu pijar yang lain 15V/0,2A
terhubung seri pada tegangan 20V.
Berapa besarnya arus pada rangkaian tersebut ?
Diketahui :
Utotal = 20 V;
U1 = 10 V;
I1 = 0,2 A;
U2 = 15 V;
I2 = 0,2 A
Ditanyakan : I
Jawaban :
Kedua lampu menyerap arus nominal sebesar 0,2 A pada tegangan seluruhnya
10 V + 15 V = 25 V. Tetapi karena tegangan total yang digunakan untuk
mencatu kedua lampu tersebut lebih kecil, maka arusnya harus ditentukan
dengan cara sebagai berikut :
I
U
;
R total
I
20 V
 0,16 A
125 Ω
Disini tahanan total masih belum diketahui, yang mana merupakan jumlah
tahanan bagian
Rtotal = 50  + 75  = 125 
Rtotal = R1 + R2 ;
Tahanan bagian dapat ditentukan dengan hukum Ohm dan selanjutnya
dimasukkan ke persamaan diatas :
R1 =
U1
;
I1
R1 
10 V
 50 Ω
0,2 A
R2 =
U2
;
I2
R2 
15 V
 75 Ω
0,2 A
3. Sebuah tahanan panas sebesar 15  terpasang untuk kuat arus
2,5 A. Sebuah tahanan kedua sebesar 35  terhubung seri.
Berapa besarnya tegangan yang harus terpasang pada tahanan
tersebut, jika kuat arusnya tetap dipertahankan ?
Buatlah gambar rangkaiannya !
Penerapan Konsep Dasar Listrik dan Elektronika
58
Tek nik I ns ta l as i L is tr ik
Diketahui :
R1 = 15 ;
I1 = 2,5 A;
R2 = 35 ;
Ditanyakan : Utotal
Jawaban :
Utotal = I . Rtotal ;
Utotal = 2,5 A . 50  = 125 V
Rtotal = R1 + R2 ;
Rtotal = 15  + 35  = 50 
R1=15 
Gambar 2.9
I=2,5 A
Skema rangkaian soal nomer 3
2.1.
R2=35 
Utotal
Pembagi tegangan tanpa beban
Pembagi tegangan terdiri atas dua tahanan (R1, R2) yang terhubung seri,
Dengan bantuannya maka tegangan terpasang (U) dapat terbagi kedalam dua
tegangan (U1, U2).
I
R1
U1
R2
U2
U
Gambar 2.10
Pembagi tegangan tanpa beban
Disini tahanan R1 dan R2 berturut-turut dialiri oleh arus I yang sama, untuk
rangkaian seri tahanan tersebut berlaku :
U1 R1
=
U2 R 2
Selanjutnya tahanan total Rtotal :
Penerapan Konsep Dasar Listrik dan Elektronika
59
Tek nik I ns ta l as i L is tr ik
U1
R
= 1
U R total
U2
R
= 2
U R total
U1
R1
=
U R1  R 2
U2
R2
=
U R1  R2
Disusun menjadi :
U1 = U
R1
R1  R 2
U1 = U
R1
R1  R 2
Rumus pembagi tegangan
Persamaan tersebut hanya berlaku, jika melalui kedua tahanan mengalir arus
yang sama, berarti bahwa pada “tap” pembagi tegangan tidak ada arus yang
diambil (pembagi tegangan tidak berbeban).
Melalui pemilihan R1 dan R2 yang sesuai, seluruh nilai tegangan dapat disetel
antara nol dan tegangan total U.
Untuk rangkaian pembagi tegangan dapat juga menggunakan suatu tahanan
dengan “tap” yang variable (dapat berubah), biasa disebut potensiometer.
R1
U
R2
U2
Gambar 2.11
Potensiometer
Contoh :
1. Sebuah pembagi tegangan tidak berbeban untuk 140 V terdiri
atas tahanan R1 = 20 k dan R2 = 40 k.
Berapa besarnya tegangan bagian (U1 dan U2) ?
Diketahui :
U = 140 V;
R1 = 20 k; R2 = 40 k
Ditanyakan : U1 dan U2
Jawaban :
U1 = U
R1
R1  R2
Penerapan Konsep Dasar Listrik dan Elektronika
60
Tek nik I ns ta l as i L is tr ik
U1 =
140 V. 20 000 Ω
140 . 20 000
140.1

V=
V = 46,67 V
20 000 Ω + 40 000 Ω
60 000
3
U2 = U
U2 =
R2
R1  R 2
140 V. 40 000 Ω 140.2

V = 93,33 V
60 000 Ω
3
2. Sebuah pembagi tegangan tidak berbeban dengan tahanan
total 20 k harus membagi tegangan 120 V kedalam tegangan
20 V dan 100 V.
Berapa besarnya tegangan bagian dan arus yang melalui
tahanan?
Diketahui :
Rtotal = 20 k =20 000 
U
= 120 V; U1 = 20 V;
U2 = 100 V
Ditanyakan : R1, R2 dan I
Jawaban :
U1
R1

;
U R total
R1  20 000 Ω
R1  R total
20 V
 3333 Ω  33,33 kΩ
120 V
Rtotal = R1 + R2 ;
R2
2.2.
U1
U
R2 = Rtotal - R1
= 20.000  - 3333  = 16.667  = 16,66 k
I=
U
R total
I=
120 V
120 V

 6 .10 - 3 A = 0,006 A  6 mA
3
20 000 Ω 20.10 Ω
Tahanan depan
Dengan bantuan tahanan yang terpasang seri pada beban, maka tegangan
pada beban dapat diperbesar. Tahanan semacam ini disebut tahanan depan.
Penerapan Konsep Dasar Listrik dan Elektronika
61
Tek nik I ns ta l as i L is tr ik
Contoh :
Sebuah lampu pijar 1,5V/0,2A melalui tahanan depan harus
dihubungkan ke tegangan yang tersedia U = 4,5 V.
Berapa besarnya tahanan depan yang harus terpasang agar data
nominal lampu pijar terpenuhi ?
I =0,2A
Ud
Rd
U L = 1,5 V
U = 4,5 V
Gambar 2.12
Rangkaian
arus dengan tahanan depan
Tahanan depan harus menyerap tegangan sebesar :
Ud = U - UL;
Ud = 4,5 V - 1,5 V = 3 V
Arus nominal lampu I = 0,2 A mengalir juga melalui tahanan depan dan disini
menimbulkan tegangan jatuh Ud = 3 V.
Dengan hukum Ohm tahanan depan dapat ditentukan sebagai berikut :
Rd =
Ud
;
I
Rd 
3V
 15 Ω
0,2 A
Tahanan depan dapat mereduksi kelebihan tegangan, didalam
tahanan tersebut terjadi panas.
Oleh karena itu tahanan depan harus mampu dialiri sebesar arus nominal
beban, jika tidak maka tahanan terbakar.
Dengan tahanan depan, suatu tegangan tidak dapat diturunkan hingga nol
seperti pada pembagi tegangan, disini untuk maksud tersebut tahanan depan
harus memiliki nilai tahanan yang tak terhingga besarnya.
Tahanan depan digunakan untuk menurunkan tegangan dan dengan demikian
menurunkan kuat arus putaran motor, lampu, alat ukur dan sebagainya.
Penerapan Konsep Dasar Listrik dan Elektronika
62
Tek nik I ns ta l as i L is tr ik
2.3.
Tegangan jatuh pada penghantar
Percobaan :
a) Sebuah lampu pijar dihubung ke tegangan sumber (misal
akumulator) melalui ampermeter dengan menggunakan kawat
yang panjang dan dengan diameter kecil.
Sebelum dan sesudah lampu dihidupkan, tegangan pada ujung
awal dan ujung akhir penghantar diperbandingkan.
I
RL
S
A
U1
Gambar 2.13
Tegangan
jatuh pada penghantar
U2
RL
Perhatikan: Sebelum lampu dihidupkan tegangan pada ujung awal dan ujung
akhir penghantar sama besarnya.
Setelah lampu dihidupkan tegangan pada ujung akhir penghantar berkurang
dibanding pada ujung awal penghantar.
Penyebab berkurangnya tegangan tersebut terletak pada tegangan jatuh
(simbol formula Ua) didalam penghantar masuk dan keluar.
Tegangan jatuh ditimbulkan oleh arus yang mengalir melalui
tahanan kawat.
b) Percobaan a) diulang dengan menambahkan lampu pijar yang
lain serta penghantarnya diperpanjang lagi.
Perhatikan: Setelah kedua lampu dihidupkan maka tegangan jatuh Ua semakin
berkurang, demikian pula pada perpanjangan penghantar.
Penyebab semakin berkurangnya tegangan jatuh disebabkan oleh semakin
besarnya arus dan semakin besarnya tahanan penghantar.
Penerapan Konsep Dasar Listrik dan Elektronika
63
Tek nik I ns ta l as i L is tr ik
Tegangan jatuh Ua pada penghantar semakin besar,
jika arus I didalam penghantar makin besar dan
jika tahanan penghantar RL makin besar.
Tegangan jatuh
Ua = I . RL
Ua Tegangan jatuh dalam V
I
Arus penghantar dalam A
RL Tahanan penghantardalam 
Tegangan jatuh merupakan penanggung jawab terjadinya kerugian pada
penghantar, dia menurunkan tegangan pada beban yang bisa jadi hingga
berada dibawah tegangan nominal yang dibutuhkan.
Atas dasar hal tersebut maka tegangan jatuh yang diijinkan untuk instalasi arus
kuat hingga 1000 V ditetapkan dalam prosent dari tegangan kerjanya (simbol
formula ua). Pada pengukuran penghantar perlu memperhatikan tegangan jatuh
yang diijinkan.
Saluran masuk rumah hingga kWh meter
ua = 0,5 %
kWh meter hingga lampu pijar dan peralatan
ua = 1,5 %
kWh meter hingga motor
ua = 3,0 %
Contoh :
Melalui penghantar alumunium dengan luas penampang 6 mm 2
dan panjang 40 m untuk satu jalur mengalir 20 A. Penghantar
terhubung pada tegangan 220 V. Berapa besarnya tegangan jatuh
dalam V dan dalam prosent dari tegangan jala-jala?
Diketahui :
A = 6 mm2 ;
l = 40 m;
I = 20 A;
U = 220 V
Ditanyakan : Ua, ua
Jawaban :
Ua = I . RL ;
Ua = 20 A . 0,371  = 7,42 V
Penerapan Konsep Dasar Listrik dan Elektronika
64
Tek nik I ns ta l as i L is tr ik
3.
RL 
2ρl
;
A
ua 
Ua  100
;
U
Ω  mm 2
2  0,0278
 40 m
m
RL 
 0,371 Ω
6 mm 2
ua =
7,42 V  100
 3,37 %
220 V
Rangkaian parallel tahanan
Suatu rangkaian parallel beberapa tahanan terbentuk, jika arus yang
ditimbulkannya terbagi dalam arus-arus cabang dan serentak mengalir menuju
tahanan-tahanan tersebut.
I
I1
I3
A I2
U
Gambar 2.14
R1
Rangkaian parallel
R2
R3
B
Bagaimana karakteristik arus, tegangan dan tahanannya, diperlihatkan melalui
pemikiran dan percobaan berikut :
Diantara kedua titik percabangan arus yaitu titik A dan B (gambar 2.14) terletak
tegangan total U. Disini semua tahanan bagian bergantung pada klem-klemnya,
semua tahanan terhubung pada tegangan yang sama U.
Dengan demikian sebagai ciri utama rangkaian parallel berlaku :
Pada suatu rangkaian parallel semua tahanan terletak pada
tegangan yang sama.
Percobaan :
Pengukuran arus I, I1, I2 dan I3 pada rangkaian yang diberikan
(gambar 2.15).
Penerapan Konsep Dasar Listrik dan Elektronika
65
Tek nik I ns ta l as i L is tr ik
I =1,1A
A
A
U=12V
I1 =
A
0,6A
R1 =
20
I =
I2 =
A 3
0,2A
0,3A
R2 =
40
R3 =
60
Gambar 2.15
Pembagian
arus pada rangkaian parallel
Hasil pengukuran:
I = 1,1 A; I1 = 0,6 A;
I2 = 0,3 A;
I3 = 0,2 A
Suatu pemikiran yang lebih terperinci tentang nilai hasil pengukuran arus
diperlihatkan oleh hubungan berikut:
Arus total adalah sama dengan jumlah arus-arus bagian (cabang).
I = I1 + I2 + I3 + . . .
Penjelasan untuk hal tersebut dalam hal ini, bahwasanya arus total hanya dibagi
melalui tiga lintasan arus, tetapi nilai seluruhnya tetap konstan.
Kita perbandingkan kuat arus dengan nilai tahanan yang ada, maka diketahui:
Pada tahanan terbesar mengalir arus terkecil dan pada tahanan
terkecil mengalir arus terbesar.
Pengertian ini dapat dibuktikan dengan hukum Ohm. Disini berlaku I 
U
. Pada
R
tegangan yang sama maka cabang dengan tahanan besar harus mengalir arus
yang kecil.
Perbandingan arus
I1 0,6 A 2


I2 0,3 A 1
I2 0,3 A 3


I3 0,2 A 2
Penerapan Konsep Dasar Listrik dan Elektronika
I1 0,6 A 3


I3 0,2 A 1
66
Tek nik I ns ta l as i L is tr ik
Dengan perbandingan yang sama, untuk tahanan yang ada
R1 20 Ω 1


R 2 40 Ω 2
R 2 40 Ω 2


R 3 60 Ω 3
R1 20 Ω 1


R 3 60 Ω 3
diperlihatkan, bahwa perbandingan-perbandingan tersebut berkebalikan.
Dengan demikian berlaku:
Arus bagian (cabang) satu sama lain berbanding terbalik sebagaimana tahanan bagian (cabang) yang ada.
mis.
I1 R 2

I2 R1
I2 R 3

I3 R 2
I1 R 3

I3 R1
Jadi arus total terbagi dalam suatu perbandingan tertentu atas arus cabang,
yang tergantung pada masing-masing tahanan.
Tahanan total, yang juga dikenal sebagai tahanan pengganti, dapat ditentukan
dengan hukum ohm (lihat gambar 2.15).
R tot 
U
I
R tot 
12 V
 10,9 Ω
1,1 A
Kita bandingkan nilai tahanan-tahanan bagian (cabang) dengan tahanan total,
maka menarik perhatian, bahwa semua tahanan bagian (cabang) lebih besar
dari pada tahanan total.
Tahanan total lebih kecil dari tahanan bagian/cabang yang terkecil.
Hal tersebut dapat diterangkan bahwa setiap merangkai tahanan secara parallel
menghasilkan arus tersendiri dari nilai tahanannya, sehingga arus total untuk
tahanan parallel menjadi meningkat, berarti tahanan totalnya berkurang dan
menjadi lebih kecil dari tahanan bagian (cabang) yang terkecil.
Penerapan Konsep Dasar Listrik dan Elektronika
67
Tek nik I ns ta l as i L is tr ik
Misal kita kombinasikan tahanan 1 dengan tahanan 1000 , maka tahanan
1000  memang hanya menghasilkan arus yang sangat kecil dibanding arus
pada tahanan 1, tetapi arus totalnya meningkat, artinya tahanan total menjadi
lebih kecil dari 1.
Setiap menghubungkan cabang parallel (tahanan parallel) menghantarkan
rangkaian arus yang lebih baik. Daya hantarnya meningkat. Maka daya hantar
total suatu rangkaian parallel menjadi
Gtot = G1 + G2 + G3 + . . .
Disini daya hantar kebalikan dari tahanan (G 
1
), diperoleh rumus
R
1
1
1
1



 
R tot R1 R 2 R 3
Seper tahanan total adalah sama dengan jumlah dari seper
tahanan bagian (cabang).
Untuk dua tahanan parallel berlaku:
1
1
1

+
R tot R 1 R 2
Dari sini penyebut disamakan menjadi R1  R2
R + R2
1
 1
R tot
R1 . R 2
atau
R tot 
R1 . R 2
R1 + R 2
Tahanan total untuk dua tahanan
yang dirangkai parallel
Penerapan Konsep Dasar Listrik dan Elektronika
68
Tek nik I ns ta l as i L is tr ik
Rangkaian parallel sangat sering digunakan didalam praktik. Praktis semua
beban dirangkai parallel pada jala-jala, dalam hal ini peralatan tersebut dibuat
untuk tegangan nominal tertentu dan pada gangguan tidak berfungsinya salah
satu peralatan semua yang lainnya tidak terpengarug olehnya (gambar 2.16).
Tahanan parallel juga dipasang, untuk mengatasi tingginya kuat arus suatu
pemakai (beban), seperti misalnya pada perluasan batas ukur suatu pengukur
arus (amperemeter).
I tot
U = 220 V
I1
I2
I3
M
Lampu
Pemanas
Motor
Gambar 2.16 Rangkaian
parallel dalam praktik
Contoh :
1. Dua tahanan R1 = 4  dan R2 = 6  dihubung parallel.
Berapa besarnya tahanan total ?
Diketahui :
R1 = 4 ;
R2 = 6 
Ditanyakan : Rtotal
Jawaban:
R tot 
R1 . R 2
R1 + R 2
R tot 
4 Ω . 6 Ω 24 Ω 2

 2,4 Ω
4 Ω + 6 Ω 10 Ω
2. Tiga tahanan R1 = 20 ; R2 = 25  dan R3 = 100  terpasang
parallel pada 100 V.
Berapa besarnya
a) tahanan total ?
b) arus total ?
Penerapan Konsep Dasar Listrik dan Elektronika
69
Tek nik I ns ta l as i L is tr ik
Diketahui :
R1 = 20 ; R2 = 25 ;
Ditanyakan :
Rtotal , Itotal
Jawaban:
Penyelesaian cara 1
R3 = 100 
1
1
1
1

+
+
R tot R1 R 2 R 3
1
1
1
1
1
1
1

+
+
 0,05  0,04  0,01
R tot 20 Ω 25 Ω 100 Ω
Ω
Ω
Ω
 0,1
1
Ω
Dengan membalik kedua sisi persamaan diperoleh
1
Ω  10 Ω
0,1
U

R tot
R tot 
Itot
Itot 
100 V
 10 A
10 Ω
Penyelesaian cara 2
I1 
U 100 V

5A
R1
20 Ω
I2 
U 100 V

4A
R2
25 Ω
I3 
U 100 V

 1A
R 3 100 Ω
Itot  I1  I2  I3
Itot  5A  4A  1A = 10 A
R tot 
U
Itot
R tot 
100 V
 10 Ω
10 A
Penerapan Konsep Dasar Listrik dan Elektronika
70
Tek nik I ns ta l as i L is tr ik
3. Pada rangkaian arus terpasang tahanan 25 . Dengan
memasang tahanan kedua secara parallel, tahanan rangkaian
harus diperkecil menjadi 5 .
Berapa nilai tahanan parallel yang memenuhi ?
Diketahui :
R1 = 25 ; Rtotal = 20 
Ditanyakan :
R2
Jawaban:
1
1
1

+
R tot R 1 R 2
1
1
1


R 2 R tot R1
1
1
1
1
1
1


 0,05  0,04  0,01
R 2 20 Ω 25 Ω
Ω
Ω
Ω
R2 
1
Ω = 100 Ω
0,01
4. Pada suatu alat pemanas terpasang parallel dua tahanan
pemanas yang sama besarnya pada tegangan 220 V dan
seluruhnya menyerap arus 11 A.
Berapa besarnya arus yang terserap, jika kedua tahanan
tersebut dihubung seri ?
Diketahui :
U = 220 V;
Itotal = 11 A
Ditanyakan :
Iseri
Jawaban:
Pada rangkaian parallel setiap tahanan pemanas menyerap
arus sebesar
I
Itot 11 A

 5,5 A
2
2
Dengan demikian diperoleh tahanan
Penerapan Konsep Dasar Listrik dan Elektronika
71
Tek nik I ns ta l as i L is tr ik
U
I
220 V
R
 40 Ω
5,5 A
R
Tahanan total dalam rangkaian seri menjadi
R tot  2  R
R tot  2  40 Ω = 80 Ω
3.1.
ISeri 
U
R tot
ISeri 
220 V
 2,75 A
80 Ω
Tahanan samping (tahanan shunt)
Dengan bantuan tahanan yang dipasang parallel pada beban, arus yang besar
pada beban dapat diatasi. Tahanan semacam ini disebut tahanan samping
(tahanan shunt).
Contoh :
Instrumen suatu pengukur arus dengan tahanan dalam 40  boleh
dibebani hingga 25 mA. Untuk memperluas batas ukur menjadi
150 mA suatu tahanan harus dipasang parallel.
Berapa nilai tahanan samping (tahanan shunt) yang sesuai ?
I =150mA I i =25mA
A
IS
Ri =40
Gambar 2.17
Alat ukur dengan tahanan shunt
RS
Tahanan samping (tahanan shunt) RS harus menyerap arus sebesar
IS = I - Ii ;
IS = 150 mA - 25 mA
Penerapan Konsep Dasar Listrik dan Elektronika
72
Tek nik I ns ta l as i L is tr ik
Tegangan jatuh pada tahanan samping (tahanan shunt) dan pada instrumen
ukur sama besarnya. Dihitung dengan hukum Ohm.
U = Ri . I i ;
U = 40  . 0,025 A = 1 V
Dengan demikian maka pada tahanan samping (tahanan shunt), besarnya
tegangan terpasang dan arus yang mengalir melalui tahanan telah diketahui,
sehingga besarnya tahanan samping (tahanan shunt) dapat ditentukan.
RS =
U
;
IS
RS =
1V
=8Ω
0,125 A
Melalui tahanan samping (tahanan shunt) sebesar 8  maka arus totalnya
terbagi, sehingga tidak terjadi beban lebih pada instrumen ukur.
Penerapan Konsep Dasar Listrik dan Elektronika
73